1.5: Transformación de funciones

Muchas veces cuando se nos da un problema, tratamos de modelar el escenario utilizando las matemáticas en forma de palabras, tablas, gráficas y ecuaciones para poder explicarlo o resolverlo. Al construir modelos, a menudo es útil construir a partir de fórmulas o modelos existentes. Conocer los gráficos básicos de las funciones de tu kit de herramientas puede ayudarte a resolver problemas al poder modelar nuevos comportamientos adaptando algo que ya conoces. Desafortunadamente, los modelos y fórmulas existentes que conocemos no siempre son exactamente los mismos que los que se presentan en los problemas que enfrentamos.

Afortunadamente, existen formas sistemáticas de cambiar, estirar, comprimir, voltear y combinar funciones para ayudarlas a convertirse en mejores modelos para los problemas que estamos tratando de resolver. Podemos transformar lo que ya sabemos en lo que necesitamos, de ahí el nombre, “Transformación de funciones”. Cuando tenemos un problema de historia, fórmula, gráfico o tabla, podemos transformar esa función de varias maneras para formar nuevas funciones.

Turnos

Ejemplo\(\PageIndex{1}\)

Para regular la temperatura en un edificio verde, los respiraderos de flujo de aire cerca del techo se abren y cierran durante todo el día para permitir que el aire caliente escape. La gráfica siguiente muestra los respiraderos abiertos\(V\) (en pies cuadrados) a lo largo del día,\(t\) en horas posteriores a la medianoche. Durante el verano, el personal de las instalaciones decide tratar de regular mejor la temperatura aumentando la cantidad de respiraderos abiertos en 20 pies cuadrados a lo largo del día. Esboza una gráfica de esta nueva función.

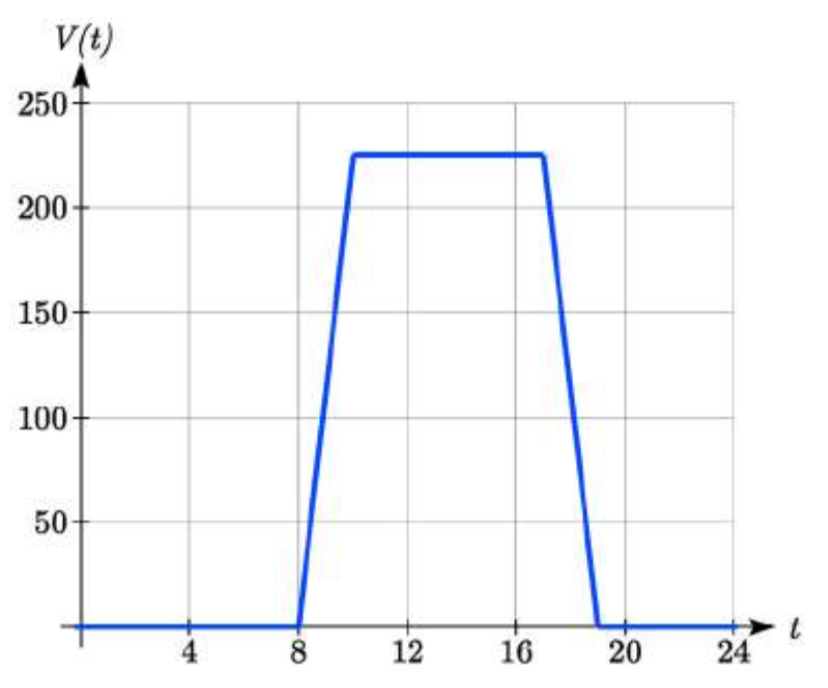
Solución

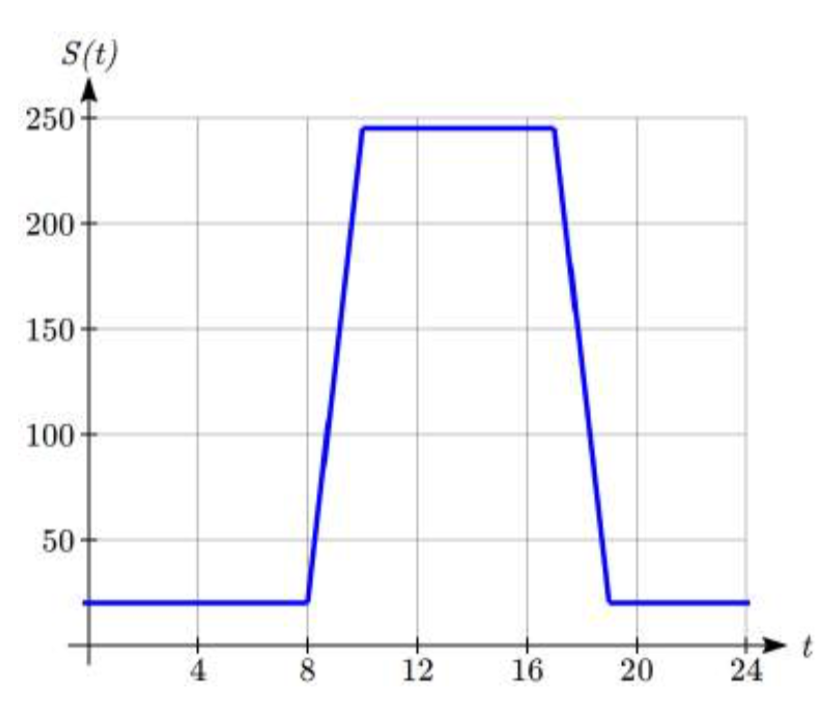Podemos esbozar una gráfica de esta nueva función agregando 20 a cada uno de los valores de salida de la función original. Esto tendrá el efecto de desplazar la gráfica hacia arriba.

Observe que en la segunda gráfica, por cada valor de entrada, el valor de salida ha aumentado en veinte, así que si llamamos a la nueva función\(S(t)\), podríamos escribir\(S(t)=V(t)+20\).

Tenga en cuenta que esta notación nos dice que para cualquier valor de\(t\), se\(S(t)\) puede encontrar evaluando la\(V\) función en la misma entrada, luego sumando veinte al resultado.

Esto define\(S\) como una transformación de la función\(V\), en este caso un desplazamiento vertical hacia arriba de 20 unidades.

Observe que con un desplazamiento vertical los valores de entrada permanecen iguales y solo cambian los valores de salida.

Definición: Desplazamiento vertical

Dada una función\(f(x)\), si definimos una nueva función\(g(x)\) como

\[g(x)=f(x)+k\]

donde\(k\) es una constante

entonces\(g(x)\) es un desplazamiento vertical de Funciones:Desplazamientos verticales de la función\(f(x)\), donde todos los valores de salida han sido aumentados en\(k\).

Si\(k\) es positivo, entonces la gráfica se desplazará hacia arriba

Si\(k\) es negativo, entonces la gráfica se desplazará hacia abajo

Ejemplo\(\PageIndex{2}\)

Una función\(f(x)\) se da como una tabla a continuación. Crear una tabla para la función\(g(x)=f(x)-3\)

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11

Solución

La fórmula nos\(g(x)=f(x)-3\) dice que podemos encontrar los valores de salida de la\(g\) función restando 3 de los valores de salida de la\(f\) función. Por ejemplo,

\[f(2) = 1\nonumber\]

se encuentra en la tabla dada

\[g(x) = f(x) - 3\nonumber\]

es nuestra transformación dada

\[g(2) = f(2) - 3 = 1 - 3 = -2\nonumber\]

Al restar 3 de cada\(f(x)\) valor, podemos completar una tabla de valores para\(g(x)\)

\(x\)	2	4	6	8
\(g(x)\)	-2	0	4	8

Al igual que con el desplazamiento vertical anterior, observe que los valores de entrada permanecen iguales y solo cambian los valores de salida.

Ejercicio\(\PageIndex{1}\)

La función\(h(t) = -4.9t^{2} + 30t\) da la altura h de una bola (en metros) lanzada hacia arriba desde el suelo después de\(t\) segundos. Supongamos que en cambio la pelota fue lanzada desde lo alto de un edificio de 10 metros. Relacionar esta nueva función de altura\(b(t)\) con\(h(t)\), luego encuentre una fórmula para\(b(t)\).

Contestar

\[b(t) = h(t) + 10 = -4.9t^2 + 30t + 10\nonumber\]

El desplazamiento vertical es un cambio en la salida, o fuera, de la función. Ahora veremos cómo los cambios a la entrada, en el interior de la función, cambian su gráfica y significado.

Ejemplo\(\PageIndex{3}\)

Volviendo a nuestro ejemplo de flujo de aire del edificio desde el inicio de la sección, supongamos que en otoño, el personal de las instalaciones decide que el plan de ventilación original comienza demasiado tarde, y quieren mover todo el programa de ventilación para comenzar dos horas antes. Haga un boceto de una gráfica de la nueva función.

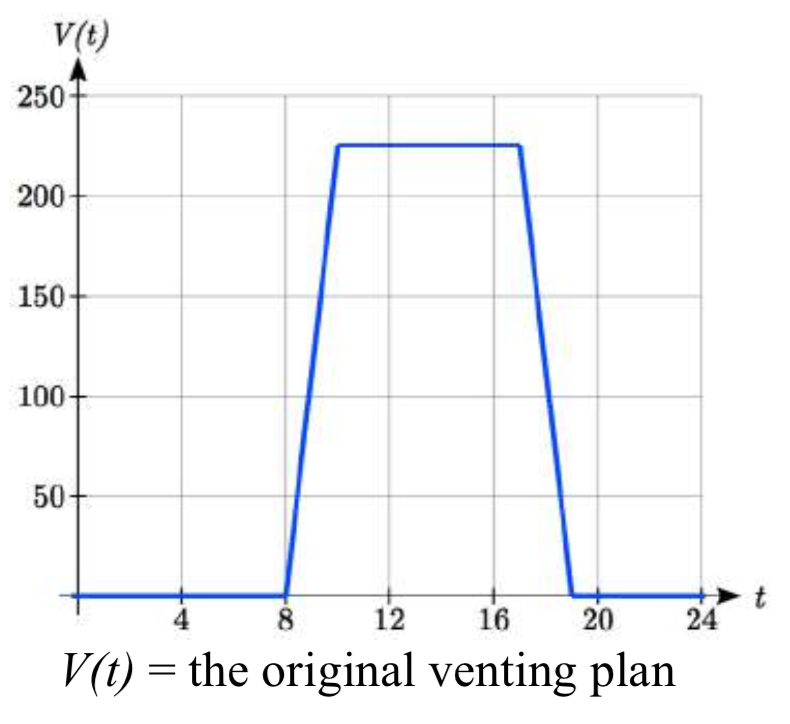
Solución

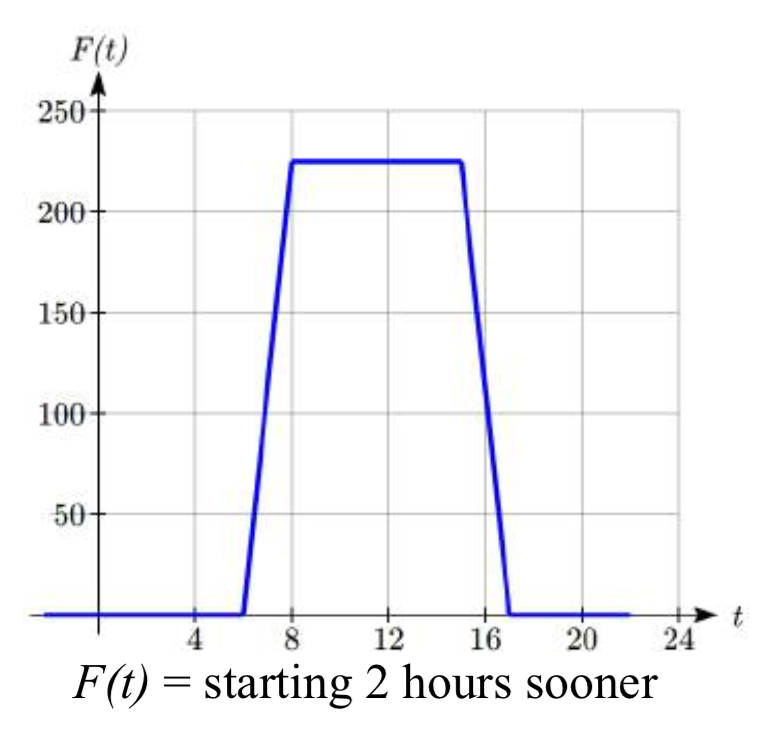
En la nueva gráfica, a la que podemos llamar\(F(t)\), en cada momento, el flujo de aire es el mismo que la función original\(V(t)\) era dos horas después. Por ejemplo, en la función original\(V\), el flujo de aire comienza a cambiar a las 8 am, mientras que para la función\(F(t)\) el flujo de aire comienza a cambiar a las 6am. Los valores de función comparables son\(V(8) = F(6)\).

Observe también que los respiraderos se abrieron primero a 220 pies cuadrados a las 10 de la mañana bajo el plan original, mientras que bajo el nuevo plan los respiraderos alcanzan los 220 pies cuadrados a las 8 a.m., así que\(V(10)=F(8)\).

En ambos casos vemos que desde que\(F(t)\) arranca 2 horas antes, se alcanzan los mismos valores de salida cuando,\(F(t)=V(t+2)\)

Tenga en cuenta que\(V(t+2)\) tuvo el efecto de desplazar la gráfica a la\(left\).

Los cambios horizontales o “cambios internos” afectan el dominio de una función (la entrada) en lugar del rango y a menudo parecen contrarios a la intuición. La nueva función\(F(t)\) utiliza las mismas salidas que\(V(t)\), pero hace coincidir esas salidas con entradas dos horas antes que las de\(V(t)\). Dicho de otra manera, debemos sumar 2 horas a la entrada de\(V\) para encontrar la salida correspondiente para\(F\):\(F(t)=V(t+2)\).

Definición: Desplazamiento horizontal

Dada una función\(f(x)\), si definimos una nueva función\(g(x)\) como

\[g(x)=f(x+k)\nonumber \]

donde\(k\) es una constante

entonces\(g(x)\) es un desplazamiento horizontal de la función\(f(x)\)

Si\(k\) es positivo, entonces la gráfica se desplazará a la izquierda

Si\(k\) es negativo, entonces la gráfica se desplazará hacia la derecha

Ejemplo\(\PageIndex{4}\)

Una función\(f(x)\) se da como una tabla a continuación. Crear una tabla para la función\(g(x)=f(x-3)\).

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11

Solución

La fórmula nos\(g(x)=f(x-3)\) dice que los valores de salida de\(g\) son los mismos que el valor de salida de f con un valor de entrada tres menor. Por ejemplo, eso lo sabemos\(f(2) = 1\). Para obtener la misma salida de la\(g\) función, necesitaremos un valor de entrada que sea 3\(larger\): Ingresamos un valor que es tres más grande\(g(x)\) porque la función quita tres antes de evaluar la función\(f\).

\[g(5)=f(5-3)=f(2)=1\nonumber \]

\(x\)	5	7	9	11
\(g(x)\)	1	3	7	11

El resultado es que la función\(g(x)\) ha sido desplazada a la derecha por 3. Observe que los valores de salida para\(g(x)\) siguen siendo los mismos que los valores de salida para\(f(x)\) en el gráfico, pero los valores de entrada correspondientes\(x\),, se han desplazado a la derecha en 3:2 desplazado a 5, 4 desplazado a 7, 6 desplazado a 9 y 8 desplazado a 11.

Ejemplo\(\PageIndex{5}\)

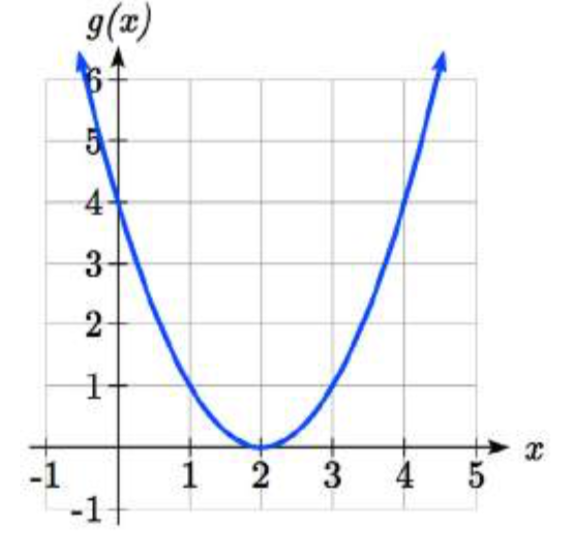
El gráfico que se muestra es una transformación de la función del kit de herramientas\(f(x)=x^{2}\). Relacionar esta nueva función\(g(x)\) con\(f(x)\), y luego encontrar una fórmula para\(g(x)\).

Solución

Observe que la gráfica se ve casi idéntica en forma a la\(f(x)=x^{2}\) función, pero los\(x\) valores se desplazan hacia las dos unidades de la derecha. El vértice solía estar en (0, 0) pero ahora el vértice está en (2, 0). La gráfica es la función cuadrática básica desplazada dos hacia la derecha, entonces

\[g(x)=f(x-2)\nonumber \]

Observe cómo debemos ingresar el valor\(x = 2\), para obtener el valor de salida\(y = 0\); los\(x\) valores deben ser dos unidades más grandes, debido al desplazamiento hacia la derecha en 2 unidades.

Luego podemos usar la definición de la\(f(x)\) función para escribir una fórmula\(g(x)\) evaluando\(f(x-2)\):

Desde\(f(x)=x^{2}\) y\(g(x)=f(x-2)\)

\[g(x)=f(x-2)=(x-2)^{2}\nonumber \]

Si te encuentras teniendo problemas para determinar si el turno es +2 o -2, podría ser útil considerar un solo punto en la gráfica. Para una cuadrática, mirar el punto más bajo es conveniente. En la función original,\(f(0)=0\). En nuestra función desplazada,\(g(2)=0\). Para obtener el valor de salida de 0 de la\(f\) función, necesitamos decidir si un +2 o -2 funcionará para satisfacer\(g(2) = f(2\ ?\ 2)=f(0)=0\). Para que esto funcione, necesitaremos restar 2 de nuestros valores de entrada.

Al pensar en los desplazamientos horizontales y verticales, es bueno tener en cuenta que los desplazamientos verticales están afectando los valores de salida de la función, mientras que los desplazamientos horizontales están afectando los valores de entrada de la función.

Ejemplo\(\PageIndex{6}\)

La función\(G(m)\) da el número de galones de gas requeridos para conducir m millas. Interpretar\(G(m)+10\) y\(G(m+10)\).

Solución

\(G(m)+10\)está sumando 10 a la salida, galones. Esto es 10 galones de gas más de lo que se requiere para conducir\(m\) millas. Entonces, este es el gas requerido para conducir\(m\) millas, más otros 10 galones de gas.

\(G(m+10)\)está sumando 10 a la entrada, millas. Esta es la cantidad de galones de gas requeridos para conducir 10 millas más que\(m\) millas.

Ejercicio\(\PageIndex{2}\)

Dado el\(f(x)=\sqrt{x}\) gráfico de funciones, la función original\(f(x)\) y la transformación\(g(x)=f(x+2)\).

a. ¿Se trata de un cambio horizontal o vertical?

b. ¿De qué manera se desplaza la gráfica y en cuántas unidades?

c. Gráfica\(f(x)\) y\(g(x)\) sobre los mismos ejes.

Contestar

a. Desplazamiento horizontal

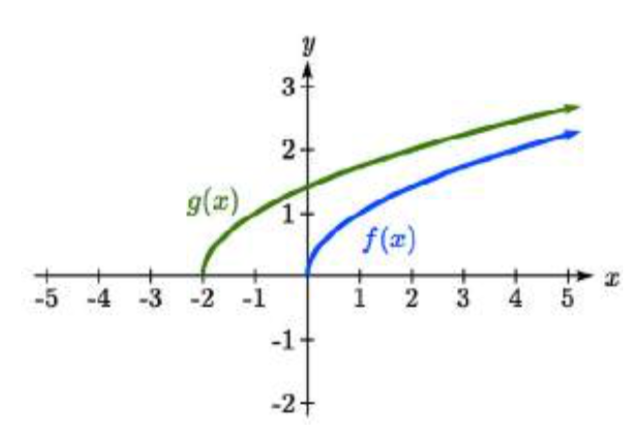
b. La función se desplaza a la IZQUIERDA en 2 unidades

c. Mostrado a la derecha

Ahora que tenemos dos transformaciones, podemos combinarlas juntas.

Recuerda:

Los desplazamientos verticales son cambios externos que afectan a los valores del eje de salida (vertical) desplazando la función transformada hacia arriba o hacia abajo.

Los desplazamientos horizontales son cambios internos que afectan a los valores del eje de entrada (horizontal) desplazando la función transformada hacia la izquierda o la derecha.

Ejemplo\(\PageIndex{7}\)

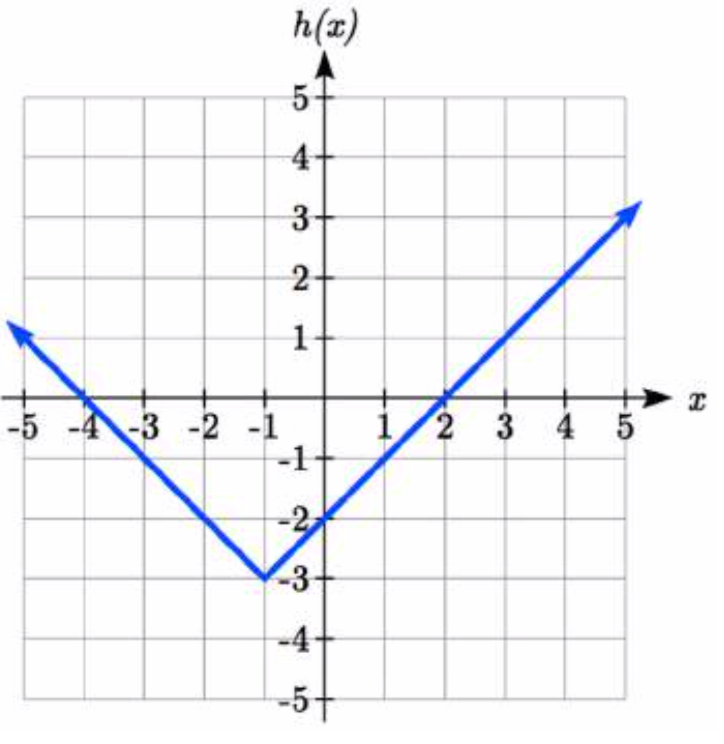
Dado\(f(x) = |x|\), esbozar una gráfica de\(h(x)=f(x+1)-3\).

Solución

La función\(f\) es nuestra función de valor absoluto de kit de herramientas. Sabemos que esta gráfica tiene una\(V\) forma, con el punto en el origen. La gráfica de se\(h\) ha transformado\(f\) de dos maneras:\(f(x+1)\) es un cambio en el interior de la función, dando un desplazamiento horizontal a la izquierda por 1, luego la resta por 3 in\(f(x+1)-3\) es un cambio al exterior de la función, dando un desplazamiento vertical hacia abajo por 3. Transformar la gráfica da

Ejemplo\(\PageIndex{8}\)

Escribe una fórmula para la gráfica mostrada, una transformación de la función de raíz cuadrada del kit de herramientas.

Solución

La gráfica de la función del kit de herramientas comienza en el origen, por lo que esta gráfica se ha desplazado 1 a la derecha, y hacia arriba 2. En notación de funciones, podríamos escribir eso como\(h(x)=f(x-1)+2\). Usando la fórmula para la función de raíz cuadrada podemos escribir

\(h(x)=\sqrt{x-1} +2\)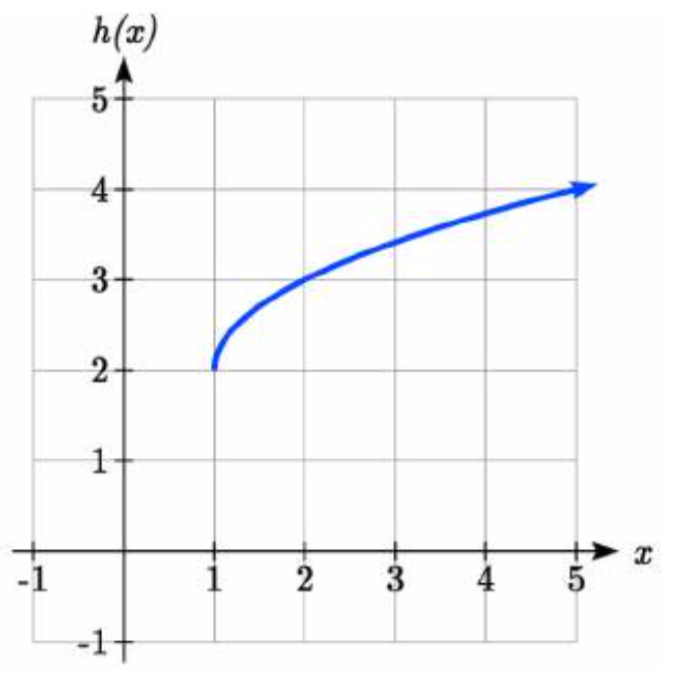

Tenga en cuenta que esta transformación ha cambiado el dominio y el rango de la función. Esta nueva gráfica tiene dominio\([1,\infty )\) y rango\([2,\infty )\).

Reflexiones

Otra transformación que se puede aplicar a una función es una reflexión sobre el eje horizontal o vertical.

Ejemplo\(\PageIndex{9}\)

Refleja la gráfica\(s(t)=\sqrt{t}\) tanto vertical como horizontalmente.

Solución

Reflejando la gráfica verticalmente, cada valor de salida se reflejará sobre el\(t\) eje horizontal:

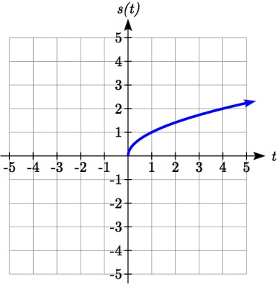
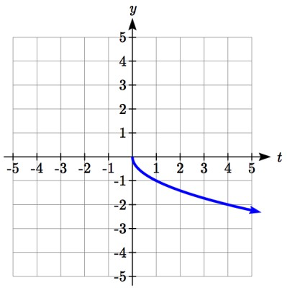
Dado que cada valor de salida es el opuesto al valor de salida original, podemos escribir

\[V(t)= -s(t)\nonumber\]

\[V(t)= -\sqrt{t}\nonumber \]

Observe que este es un cambio externo o cambio vertical que afecta a los valores de salida s (t) por lo que el signo negativo pertenece fuera de la función.

Reflejando horizontalmente, cada valor de entrada se reflejará sobre el eje vertical.

Dado que cada valor de entrada es lo opuesto al valor de entrada original, podemos escribir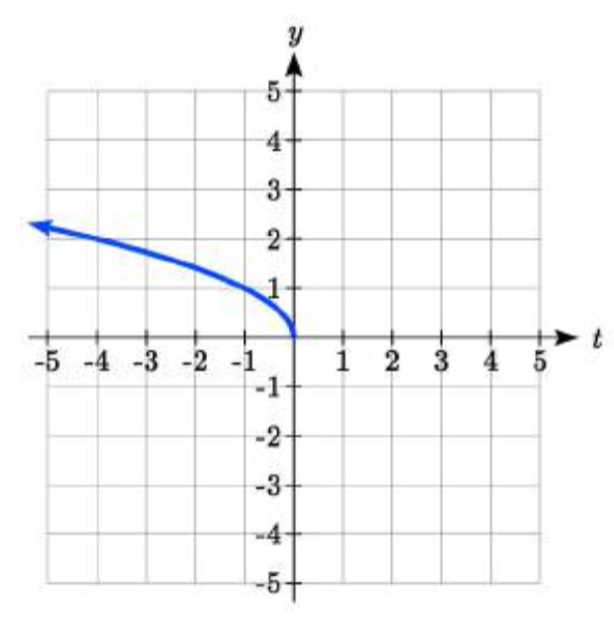

\[H(t)=s(-t)\nonumber \]

\[H(t)=\sqrt{-t}\nonumber \]

Observe que este es un cambio interior o cambio horizontal que afecta los valores de entrada por lo que el signo negativo está en el interior de la función.

Tenga en cuenta que estas transformaciones pueden afectar el dominio y rango de las funciones. Mientras que la función raíz cuadrada original tiene dominio\([0,\infty )\) y rango\([0,\infty )\), la reflexión vertical le da a la\(V(t)\) función el rango\((-\infty ,0]\), y la reflexión horizontal le da a la\(H(t)\) función el dominio\((-\infty ,0]\).

Definición: reflexiones

Dada una función\(f(x)\), si definimos una nueva función\(g(x)\) como

\[g(x)=-f(x),\]

entonces\(g(x)\) es una reflexión vertical de la función\(f(x)\), a veces llamada reflexión sobre el\(x\) eje -eje

Si definimos una nueva función\(g(x)\) como

\[g(x)=f(-x),\]

entonces\(g(x)\) es una reflexión horizontal de la función\(f(x)\), a veces llamada reflexión sobre el\(y\) eje -eje

Ejemplo\(\PageIndex{10}\)

Una función\(f(x)\) se da como una tabla a continuación. Crear una tabla para la función\(g(x)=-f(x)\) y\(h(x)=f(-x)\)

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11

Solución

Porque\(g(x)\), esto es una reflexión vertical, por lo que los\(x\) valores permanecen iguales y cada valor de salida será el opuesto al valor de salida original

Porque\(h(x)\), esto es una reflexión horizontal, y cada valor de entrada será el opuesto al valor de entrada original y los\(h(x)\) valores permanecerán iguales que los\(f(x)\) valores:

\(x\)	-2	-4	-6	-8
\(h(x)\)	1	3	7	11

Ejemplo\(\PageIndex{11}\)

Un modelo común para el aprendizaje tiene una ecuación similar a\(k(t)=-2^{-t} +1\), donde\(k\) está el porcentaje de dominio que se puede lograr después de las sesiones de\(t\) práctica. Esta es una transformación de la función que aquí\(f(t)=2^{t}\) se muestra. Esbozar una gráfica de\(k(t)\).

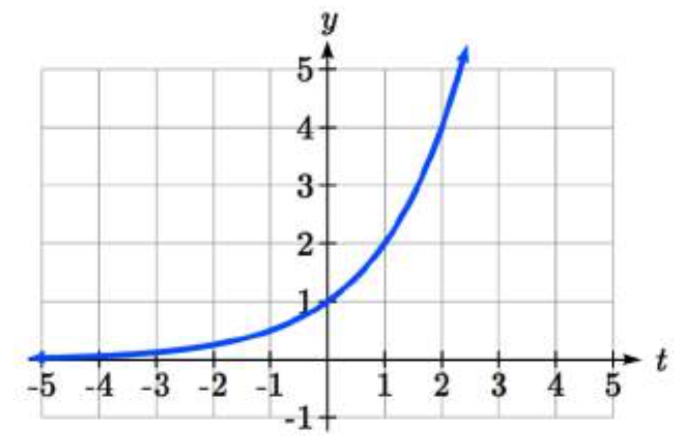
Solución

Esta ecuación combina tres transformaciones en una sola ecuación.

Una reflexión horizontal:\(f(-t)=2^{-t}\) combinada con

Una reflexión vertical:\(-f(-t)=-2^{-t}\) combinada con

Un cambio vertical hacia arriba 1:\(-f(-t)+1=-2^{-t} +1\)

Podemos esbozar una gráfica aplicando estas transformaciones una a la vez a la función original:

El gráfico original Reflejado horizontalmente Luego reflejado verticalmente

El Gráfico Original Reflejado Horizontalmente El Reflejado

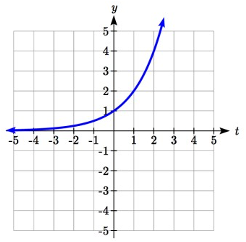
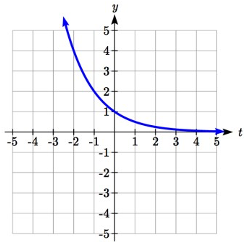
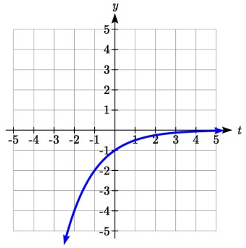
Entonces, después de subir 1, obtenemos la gráfica final.

\[k(t)=-f(-t)+1=-2^{-t} +1\nonumber \]

Nota: Como modelo de aprendizaje, esta función estaría limitada a un dominio de\(t\ge 0\), con rango correspondiente\([0,1)\).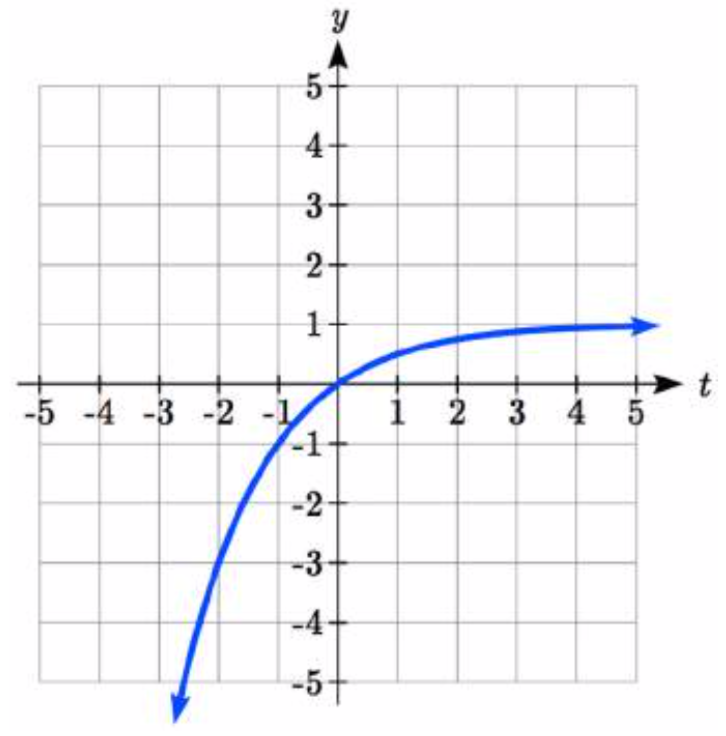

ejercicio\(\PageIndex{3}\)

Dada la función del kit de herramientas\(f(x)=x^{2}\), gráfico\(g(x) = -f(x)\) y\(h(x) = f(-x)\). ¿Te das cuenta de algo sorprendente?

Contestar

Se muestra en la gráfica

Aviso:\(g(x) = f(-x)\) se ve igual que\(f(x)\)

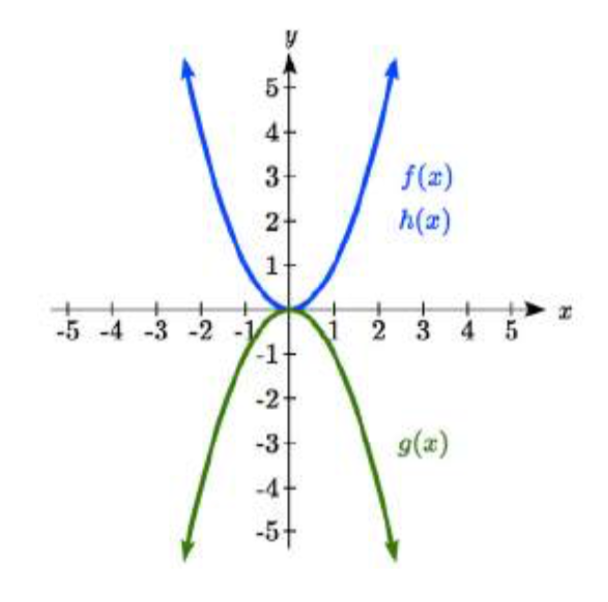
Algunas funciones exhiben simetría, en la que las reflexiones dan como resultado la gráfica original. Por ejemplo, reflejar las funciones del kit de herramientas\(f(x)=x^{2}\) o\(f(x)=|x|\) sobre el eje y resultará en la gráfica original. Llamamos a este tipo de gráficas simétricas sobre el eje y.

Asimismo, si las gráficas de\(f(x)=x^{3}\) o\(f(x)=\dfrac{1}{x}\) se reflejaran sobre ambos ejes, el resultado sería la gráfica original:

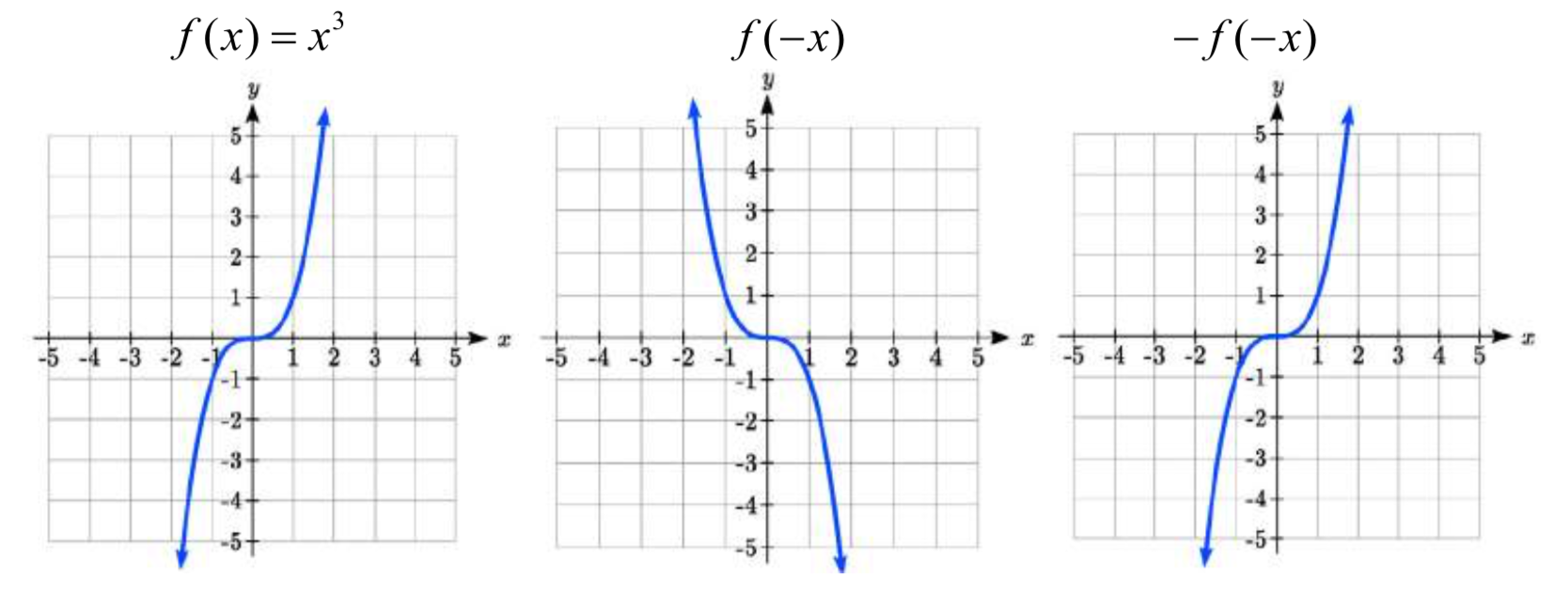
Llamamos a estas gráficas simétricas sobre el origen.

Definición: funciones pares e impares

Una función se llama función par si

\[f(x)=f(-x)\]

La gráfica de una función par es simétrica alrededor del eje vertical

Una función se llama una función impar si

\[f(x)=-f(-x)\]

La gráfica de una función impar es simétrica sobre el origen

Nota: Una función no puede ser ni par ni impar si no presenta ninguna simetría. Por ejemplo, la\(f(x)=2^{x}\) función no es ni par ni impar.

Ejemplo\(\PageIndex{12}\)

¿La función es\(f(x)=x^{3} +2x\) par, impar o ninguna?

Solución

Sin mirar una gráfica, podemos determinar esto encontrando fórmulas para las reflexiones, y viendo si nos devuelven a la función original:

\[f(-x)=(-x)^{3} +2(-x)=-x^{3} -2x\nonumber \]

Esto no nos devuelve a la función original, por lo que esta función no es parejo.

Ahora podemos intentar aplicar también una reflexión horizontal:

\[-f(-x)=-(-x^{3} -2x)=x^{3} +2x\nonumber \]

Ya que\(-f(-x)=f(x)\), esta es una función impar.

Estiramientos y Compresiones

Con los turnos, vimos el efecto de sumar o restar a las entradas o salidas de una función. Ahora exploramos los efectos de multiplicar las entradas o salidas.

Recuerde, podemos transformar el interior (valores de entrada) de una función o podemos transformar el exterior (valores de salida) de una función. Cada cambio tiene un efecto específico que se puede ver gráficamente.

Ejemplo\(\PageIndex{13}\)

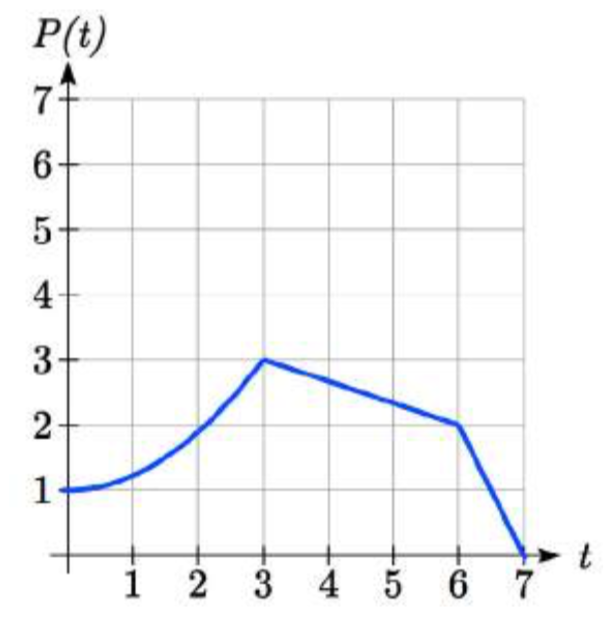
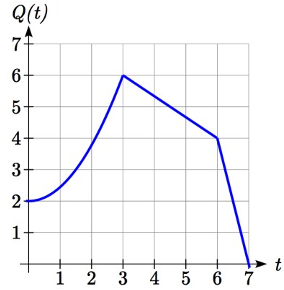
Una función\(P(t)\) modela el crecimiento de una población de moscas de la fruta. El crecimiento se muestra en la gráfica. Un científico está comparando esto con otra población,\(Q\), que crece de la misma manera, pero comienza el doble de grande. Esbozar una gráfica de esta población.

Solución

Dado que la población es siempre el doble de grande, los valores de salida de la nueva población son siempre el doble de los valores de salida de la función original. Gráficamente, esto se vería como la segunda gráfica que se muestra.

Simbólicamente,\(Q(t)=2P(t)\)

Esto significa que para cualquier entrada t, el valor de la\(Q\) función es el doble del valor de la\(P\) función. Observe que el efecto en la gráfica es un estiramiento vertical de la gráfica, donde cada punto duplica su distancia desde el eje horizontal. Los valores de entrada,\(t\), permanecen iguales mientras que los valores de salida son dos veces más grandes que antes.

Definición: Estiramiento/compresión vertical

Dada una función\(f(x)\), si definimos una nueva función\(g(x)\) como

\(g(x)=kf(x)\), donde\(k\) es una constante

entonces\(g(x)\) es un estiramiento vertical o compresión de la función\(f(x)\).

Si\(k > 1\), entonces la gráfica se estirará

Si\(0 < k < 1\), entonces la gráfica se comprimirá

Si\(k < 0\), entonces habrá combinación de un estiramiento vertical o compresión con una reflexión vertical

Ejemplo\(\PageIndex{14}\)

Una función\(f(x)\) se da como una tabla a continuación. Crear una tabla para la función\(g(x)=\dfrac{1}{2} f(x)\)

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11

Solución

La fórmula nos\(g(x)=\dfrac{1}{2} f(x)\) dice que los valores de salida de\(g\) son la mitad de los valores de salida de\(f\) con las mismas entradas. Por ejemplo, eso lo sabemos\(f(4)=3\). Entonces\[g(4)=\dfrac{1}{2} f(4)=\dfrac{1}{2} (3)=\dfrac{3}{2}\nonumber \]

\(x\)	2	4	6	8
\(g(x)\)	1/2	3/2	7/2	11/2

El resultado es que la función\(g(x)\) ha sido comprimida verticalmente por 1/2. Cada valor de salida se ha cortado a la mitad, por lo que la gráfica ahora sería la mitad de la altura original.

Ejemplo\(\PageIndex{15}\)

El gráfico que se muestra es una transformación de la función del kit de herramientas\(f(x)=x^{3}\). Relacionar esta nueva función\(g(x)\) con\(f(x)\), luego encontrar una fórmula para\(g(x)\).

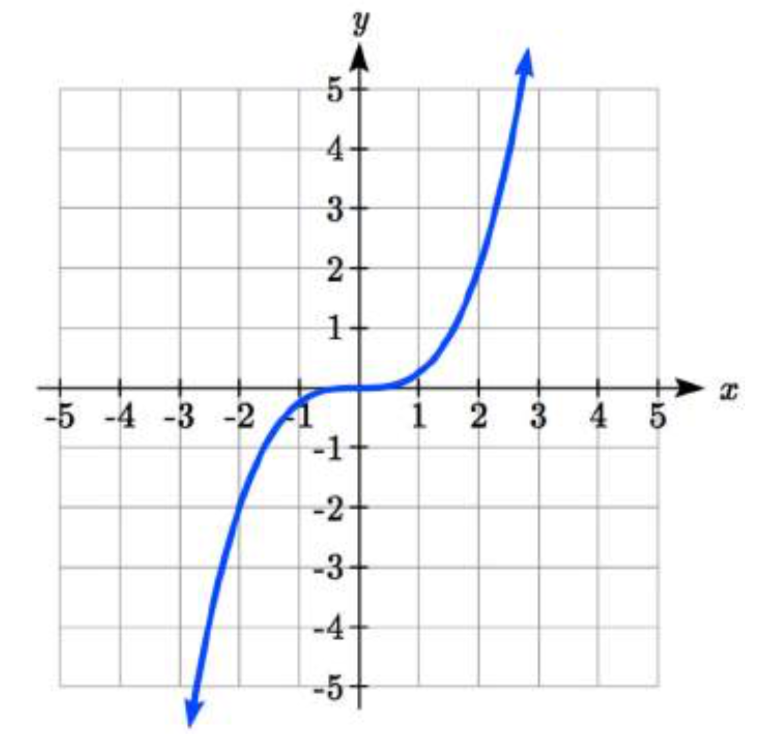
Solución

Al intentar determinar un estiramiento o desplazamiento vertical, es útil buscar un punto en la gráfica que sea relativamente claro. En esta gráfica, aparece que\(g(2)=2\). Con la función cúbica básica en la misma entrada,

\[f(2)=2^{3} =8\nonumber \]

En base a eso, parece que las salidas de\(g\) son 1/4 las salidas de la función\(f\), ya que

\[g(2)=\dfrac{1}{4} f(2)\nonumber \]

De esto podemos concluir con bastante seguridad que:

\[g(x)=\dfrac{1}{4} f(x)\nonumber \]

Podemos escribir una fórmula para\(g\) usando la definición de la función\(f\)

\[g(x)=\dfrac{1}{4} f(x)=\dfrac{1}{4} x^{3}\nonumber \]

Ahora consideramos cambios en el interior de una función.

Ejemplo\(\PageIndex{16}\)

Volviendo a la población de moscas de la fruta que vimos antes, supongamos que el científico la está comparando ahora con una población que progresa a lo largo de su vida dos veces más rápida que la población original. Es decir, esta nueva población,\(R\), avanzará en 1 hora la misma cantidad que hizo la población original en 2 horas, y en 2 horas, avanzará tanto como lo hizo la población original en 4 horas. Esbozar una gráfica de esta población.

Solución

Simbólicamente, podríamos escribir

\[R(1) = P(2)\nonumber \]

\[R(2) = P(4)\nonumber \]

y en general,

\[R(t)=P(2t)\nonumber \]

Graficando esto,

Población Original,\(P(t)\) Transformada,\(R(t)\)

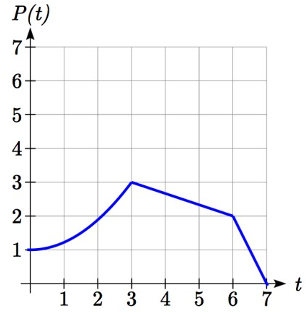
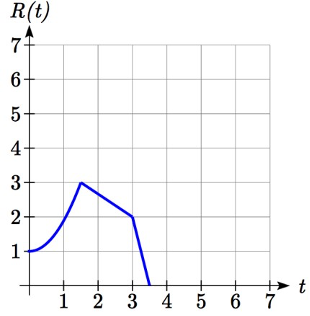
Tenga en cuenta que el efecto en la gráfica es una compresión horizontal, donde todos los valores de entrada están a la mitad de su distancia original del eje vertical.

Definición: estiramiento/compresión horizontal

Dada una función\(f(x)\), si definimos una nueva función\(g(x)\) como

\(g(x)=f(kx)\), donde\(k\) es una constante

entonces\(g(x)\) es un estiramiento horizontal o compresión de la función\(f(x)\).

Si\(k > 1\), entonces la gráfica será comprimida por 1/\(k\)

Si\(0 < k < 1\), entonces la gráfica se estirará en 1/\(k\)

Si\(k < 0\), entonces habrá combinación de un estiramiento o compresión horizontal con una reflexión horizontal.

Ejemplo\(\PageIndex{17}\)

Una función\(f(x)\) se da como una tabla a continuación. Crear una tabla para la función\(g(x)=f(\dfrac{1}{2} x)\)

\(x\)	2	4	6	8
\(f(x)\)	1	3	7	11

Solución

La fórmula nos\(g(x)=f(\dfrac{1}{2} x)\) dice que los valores de salida para g son los mismos que los valores de salida para la función\(f\) en una entrada de la mitad del tamaño. Observe que no tenemos suficiente información para determinar\(g(2)\) desde entonces\(g(2)=f(\dfrac{1}{2} \cdot 2)=f(1)\), y no tenemos un valor para\(f(1)\) en nuestra tabla. Nuestros valores de entrada a g necesitarán ser dos veces más grandes para obtener entradas para f que podamos evaluar. Por ejemplo, podemos determinar\(g(4)\) ya\(g(4)=f(\dfrac{1}{2} \cdot 4)=f(2)=1\).

\(x\)	4	8	12	16
\(g(x)\)	1	3	7	11

Dado que cada valor de entrada se ha duplicado, el resultado es que la función g (x) se ha estirado horizontalmente en 2.

Ejemplo\(\PageIndex{18}\)

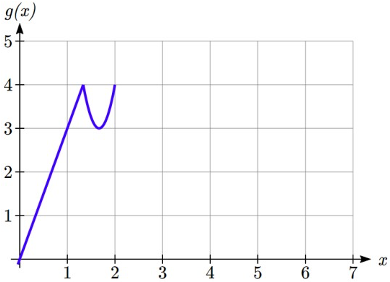
A continuación se muestran dos gráficas. Relacionar la función\(g(x)\) con\(f(x)\).

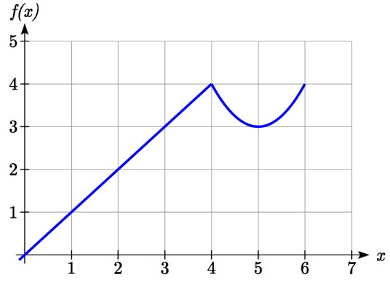
Solución

La gráfica de\(g(x)\) se parece a la gráfica de comprimida\(f(x)\) horizontalmente. Ya que\(f(x)\) termina en (6,4) y\(g(x)\) termina en (2,4) podemos ver que los\(x\) valores han sido comprimidos en 1/3, porque 6 (1/3) = 2. También podríamos notar eso\(g(2) = f(6)\), y\(g(1)=f(3)\). De cualquier manera, podemos describir esta relación como\(g(x)=f(3x)\). Esta es una compresión horizontal por 1/3.

Observe que el coeficiente necesario para un estiramiento o compresión horizontal es el\(reciprocal\) del estiramiento o compresión. Para estirar la gráfica horizontalmente por 4, necesitamos un coeficiente de 1/4 en nuestra función:\(f(\dfrac{1}{4} x)\). Esto significa que los valores de entrada deben ser cuatro veces mayores para producir el mismo resultado, requiriendo que la entrada sea mayor, provocando el estiramiento horizontal.

ejercicio\(\PageIndex{4}\)

Escribe una fórmula para la función de raíz cuadrada del kit de herramientas estirada horizontalmente por tres.

Contestar

\[g(x) = f(\dfrac{1}{3}x\nonumber \]así que usando la función de raíz cuadrada obtenemos

\[g(x) = \sqrt{\dfrac{1}{3} x}\nonumber \]

Es útil señalar que para la mayoría de las funciones del kit de herramientas, se puede representar de otras maneras un estiramiento horizontal o un estiramiento vertical. Por ejemplo, una compresión horizontal de la función\(f(x)=x^{2}\) por ½ resultaría en una nueva función\(g(x)=(2x)^{2}\), pero esto también se puede escribir como\(g(x)=4x^{2}\), un estiramiento vertical de\(f(x)\) por 4. Al escribir una fórmula para un kit de herramientas transformado, solo necesitamos encontrar una transformación que produzca la gráfica.

Combinando Transformaciones

Al combinar transformaciones, es muy importante considerar el orden de las transformaciones. Por ejemplo, el desplazamiento vertical en 3 y luego el estiramiento vertical en 2 no crea la misma gráfica que el estiramiento vertical por 2 y luego el desplazamiento vertical en 3.

Cuando vemos una expresión como\(2f(x)+3\), ¿con qué transformación debemos comenzar? La respuesta aquí sigue muy bien desde el orden de las operaciones, para las transformaciones externas. Dado el valor de salida de\(f(x)\), primero multiplicamos por 2, provocando el estiramiento vertical, luego sumamos 3, provocando el desplazamiento vertical. (Multiplicación antes de la suma)

Definición: combinar transformación vertical

Al combinar transformaciones verticales escritas en la forma\(af(x)+k\),

primero estirar verticalmente por\(a\), luego desplazar verticalmente por\(k\).

Las transformaciones horizontales son un poco más difícil de pensar. Cuando escribimos\(g(x)=f(2x+3)\) por ejemplo, tenemos que pensar en cómo las entradas a la\(g\) función se relacionan con las entradas a la\(f\) función. Supongamos que sabemos\(f(7)=12\). ¿Qué insumo\(g\) produciría esa salida? En otras palabras, ¿qué valor de\(x\) permitirá\(g(x)=f(2x+3)=f(12)\)? Nosotros necesitaríamos\(2x+3=12\). Para resolver\(x\), primero restaríamos 3, resultando en desplazamiento horizontal, luego dividiríamos por 2, causando una compresión horizontal.

definición:combinar transformaciones horizontales

Al combinar transformaciones horizontales escritas en la forma\(f(bx+p)\),

primero desplazar horizontalmente por\(p\), luego estirar horizontalmente por 1/\(b\).

Este formato termina siendo muy difícil de trabajar, ya que suele ser mucho más fácil estirar horizontalmente una gráfica antes de cambiarla. Podemos solucionar esto factorizando dentro de la función.

\[f(bx+p)= f(b(x+\dfrac{p}{b}))\]

Factorizar de esta manera nos permite estirar horizontalmente primero, luego desplazarnos horizontalmente.

Definición: combinar transformaciones horizontales (forma factorizada)

Al combinar transformaciones horizontales escritas en la forma\(f(b(x+h))\),

primero se estira horizontalmente por 1/\(b\), luego se desplaza horizontalmente por\(h\).

Definición: independencia de transformaciones horizontales y verticales

Las transformaciones horizontales y verticales son independientes. No importa si las transformaciones horizontales o verticales se realizan primero.

Ejemplo\(\PageIndex{19}\)

Dada la tabla de valores para la función\(f(x)\) a continuación, cree una tabla de valores para la función\(g(x)=2f(3x)+1\)

\(x\)	6	12	18	24
\(f(x)\)	10	14	15	17

Solución

Hay 3 pasos para esta transformación y trabajaremos de adentro hacia afuera. Comenzando con las transformaciones horizontales,\(f(3x)\) es una compresión horizontal por 1/3, lo que significa que multiplicamos cada\(x\) valor por 1/3.

\(x\)	2	4	6	8
\(f(3x)\)	10	14	15	17

Mirando ahora a las transformaciones verticales, comenzamos con el estiramiento vertical, que multiplicará los valores de salida por 2. Esto lo aplicamos a la transformación anterior.

\(x\)	2	4	6	8
\(2f(3x)\)	20	28	30	34

Finalmente, podemos aplicar el desplazamiento vertical, que agregará 1 a todos los valores de salida.

\(x\)	2	4	6	8
\(g(x) = 2f(3x) + 1\)	21	29	31	35

Ejemplo\(\PageIndex{20}\)

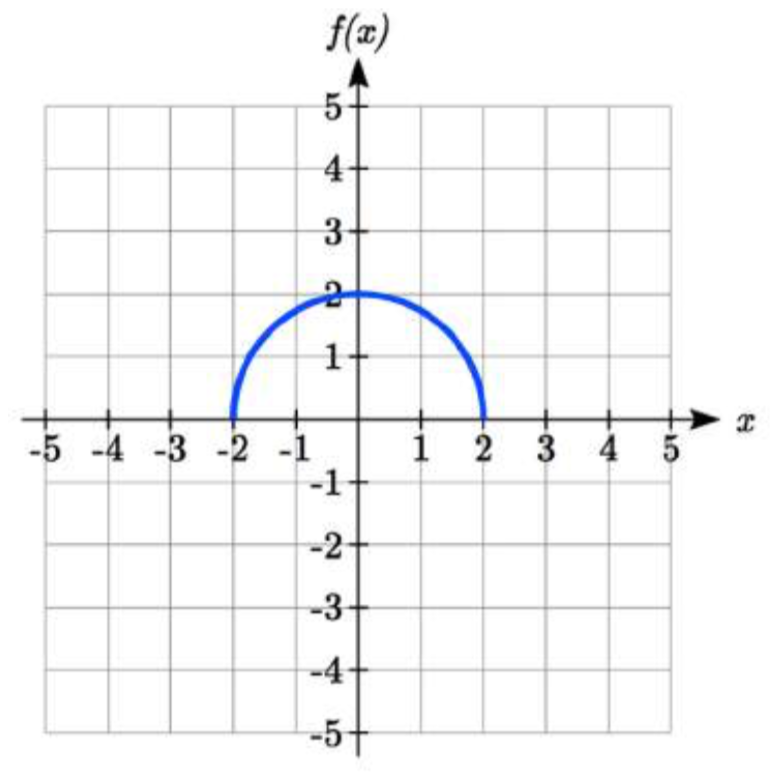
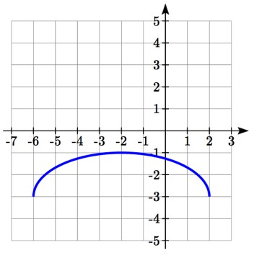
Usando la gráfica de\(f(x)\) abajo, esboza una gráfica de\(k(x)=f(\dfrac{1}{2} x+1)-3\)

Solución

Para hacer las cosas más simples, comenzaremos factorizando el interior de la función

\[f(\dfrac{1}{2} x+1)-3=f(\dfrac{1}{2} (x+2))-3\nonumber \]

Al factorizar el interior, primero podemos estirar horizontalmente por 2, como lo indica el 1/2 en el interior de la función. Recuerde que dos veces el tamaño de 0 sigue siendo 0, por lo que el punto (0,2) permanece en (0,2) mientras que el punto (2,0) se estirará hasta (4,0).

A continuación, desplazamos horizontalmente a la izquierda por 2 unidades, como lo indica el\(x+2\).

Por último, desplazamos verticalmente hacia abajo en 3 para completar nuestro boceto, como lo indica el -3 en el exterior de la función.

Estiramiento horizontal por 2 Desplazamiento horizontal a la izquierda por 2 Desplazamiento vertical

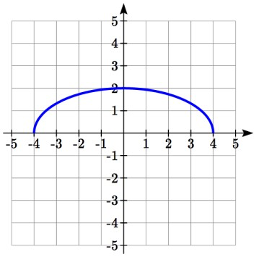
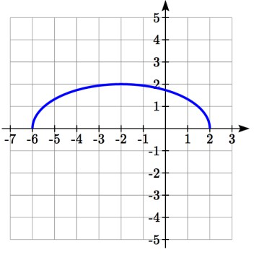
Ejemplo\(\PageIndex{21}\)

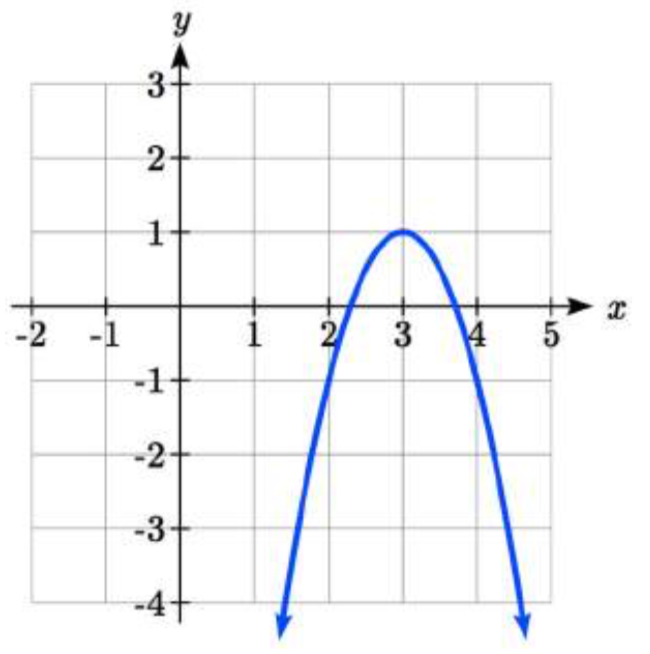
Escribe una ecuación para la gráfica transformada de la función cuadrática mostrada.

Solución

Dado que esta es una función cuadrática, primero considere cómo se ve la función básica del kit de herramientas cuadráticas y cómo ha cambiado esto. Observando la gráfica, observamos varias transformaciones:

La función del kit de herramientas original se ha volteado sobre el eje x, se ha producido algún tipo de estiramiento o compresión, y podemos ver un desplazamiento hacia la derecha 3 unidades y un cambio hacia arriba 1 unidad.

En total hay cuatro operaciones:

Reflexión vertical, que requiere un signo negativo fuera de la función

Estiramiento Vertical o Compresión Horizontal\({}^{*}\)

Desplazamiento Horizontal Derecha 3 unidades, lo que nos indica poner x -3 en el interior de la función

Vertical Shift up 1 unidad, diciéndonos que agreguemos 1 en el exterior de la función

\({}^{*\ }\)No está claro de la gráfica si está mostrando un estiramiento vertical o una compresión horizontal. Para el cuadrático, resulta que podríamos representarlo de cualquier manera, así que usaremos un estiramiento vertical. Es posible que pueda determinar el estiramiento vertical por observación.

Por observación, la función básica del kit de herramientas tiene un vértice en (0, 0) y puntos simétricos en (1, 1) y (-1, 1). Estos puntos son una unidad hacia arriba y una unidad por encima del vértice. Los nuevos puntos en la gráfica transformada están a una unidad horizontalmente pero a 2 unidades verticalmente. Se han estirado verticalmente por dos.

No todo el mundo puede ver esto simplemente mirando la gráfica. Si puedes, genial, pero si no, podemos resolverlo. Primero, escribiremos la ecuación para esta gráfica, con un estiramiento vertical desconocido.

\(f(x)=x^{2}\)La función original

\(-f(x)=-x^{2}\)Reflejado verticalmente

\(-af(x)=-ax^{2}\)Estirados verticalmente

\(-af(x-3)=-a(x-3)^{2}\)Desplazado derecho 3

\(-af(x-3)+1=-a(x-3)^{2} +1\)Desplazado hacia arriba 1

Ahora sabemos que nuestra gráfica va a tener una ecuación de la forma\(g(x)=-a(x-3)^{2} +1\). Para encontrar el estiramiento vertical, podemos identificar cualquier punto de la gráfica (que no sea el punto más alto), como el punto (2, -1), que nos dice\(g(2)=-1\). Usando nuestra fórmula general, y sustituyendo 2 por\(x\), y -1 por\(g(x)\)

\[\begin{array}{l} {-1=-a(2-3)^{2} +1} \\ {-1=-a+1} \\ {-2=-a} \\ {2=a} \end{array}\nonumber \]

Esto nos dice que para producir la gráfica necesitamos un estiramiento vertical por dos.

La función que produce esta gráfica es por lo tanto\(g(x)=-2(x-3)^{2} +1\).

Ejercicio\(\PageIndex{5}\)

Considera la función lineal\(g(x)=-2x+1\). Describir su transformación en palabras utilizando la función del kit de herramientas de identidad\(f(x) = x\) como referencia.

Contestar

La función del kit de herramientas de identidad se\(f(x) = x\) ha transformado en 3 pasos

a. Estirada verticalmente por 2.

b. Reflejado verticalmente sobre el\(x\) eje.

c. Desplazado verticalmente hacia arriba en 1 unidad.

Ejemplo\(\PageIndex{22}\)

¿En qué intervalo (s)\(g(x)=\dfrac{-2}{(x-1)^{2} } +3\) aumenta y disminuye la función?

Solución

Esta es una transformación de la función cuadrada recíproca del kit de herramientas,\(f(x)=\dfrac{1}{x^{2} }\):

\(-2f(x)=\dfrac{-2}{x^{2} }\)Un volteo vertical y estiramiento vertical por 2

\(-2f(x-1)=\dfrac{-2}{(x-1)^{2} }\)Un desplazamiento a la derecha por 1

\(-2f(x-1)+3=\dfrac{-2}{(x-1)^{2} } +3\)Un cambio hacia arriba por 3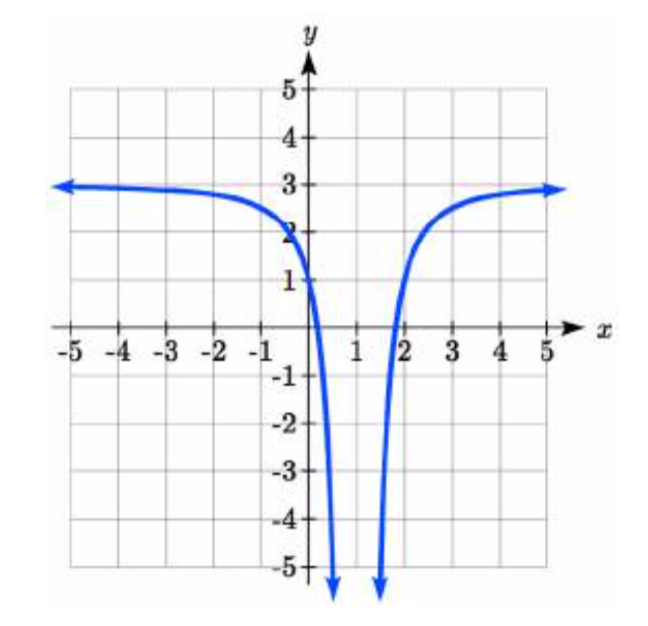

La función básica recíproca al cuadrado es creciente\((-\infty ,0)\) y decreciente sobre\((0,\infty )\). Debido al giro vertical, la\(g(x)\) función estará disminuyendo a la izquierda y aumentando a la derecha. El desplazamiento horizontal a la derecha en 1 también desplazará estos intervalos a la derecha. A partir de esto, podemos determinar que\(g(x)\) va a aumentar\((1,\infty )\) y disminuir en\((-\infty ,1)\). También podríamos graficar la transformación para ayudarnos a determinar estos intervalos.

Ejercicio\(\PageIndex{6}\)

¿En qué intervalo (s) es la función\(h(t)=(t-3)^{3} +2\) cóncava arriba y abajo?

Contestar

\(h(t)\)es cóncavo hacia abajo\((-\infty, 3)\) y cóncavo hacia arriba en\((3, \infty)\)

Temas Importantes de esta Sección

Transformaciones

Desplazamiento vertical (arriba y abajo)

Desplazamientos horizontales (izquierda y derecha)

Reflexiones sobre el eje vertical y horizontal

Funciones pares e impares

Estiramientos Verticales y Compresiones

Estiramientos y Compresiones Horizontales

Combinaciones de Transformación