3.2: Funciones cuadráticas

Última actualización
Guardar como PDF

Page ID: 116413

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, exploraremos la familia de polinomios de 2${}^{nd}$ grados, las funciones cuadráticas. Si bien comparten muchas características de polinomios en general, los cálculos involucrados en trabajar con cuadráticos suelen ser un poco más simples, lo que los convierte en un buen lugar para comenzar nuestra exploración del comportamiento a corto plazo. Además, las cuadráticas suelen surgir de problemas relacionados con el movimiento de área y proyectil, proporcionando algunas aplicaciones interesantes.

Ejemplo$\PageIndex{1}$

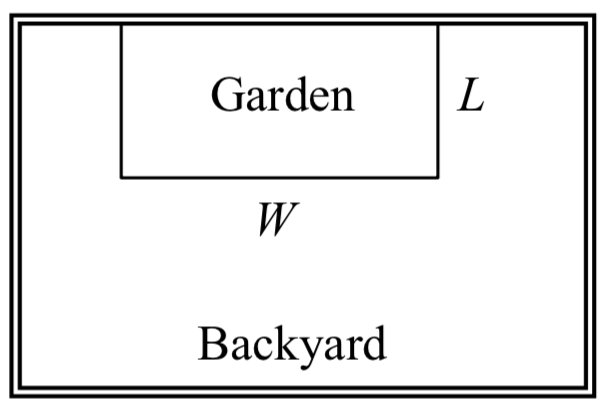
Un granjero de patio trasero quiere encerrar un espacio rectangular para un nuevo jardín. Ella ha comprado 80 pies de cercado de alambre para encerrar 3 lados, y pondrá el${}^{th}$ lado 4 contra la barda del patio trasero. Encuentre una fórmula para el área encerrada por la barda si los lados del cercado perpendiculares a la barda existente tienen longitud$L$.

$Un área rectangular está etiquetada como Patio trasero. En su interior hay un rectángulo más pequeño etiquetado como Jardín, con un lado hacia arriba contra el borde del patio trasero. Las dimensiones del jardín están etiquetadas W y L.$

Solución

En un escenario como este que involucra geometría, a menudo es útil dibujar un cuadro. También podría ser útil introducir una variable temporal,$W$, para representar el lado de la cerca paralela a la cerca${}^{th}$ lateral 4 o patio trasero.

Ya que sabemos que solo tenemos 80 pies de barda disponibles, lo sabemos$L+W+L=80$, o más simplemente,$2L+W=80$. Esto nos permite representar el ancho,$W$, en términos de$L$:\[W=80-2L\nonumber \]

Ahora estamos listos para escribir una ecuación para el área que encierra la barda. Sabemos que el área de un rectángulo es longitud multiplicada por ancho, entonces

\[A=LW=L(80-2L)\nonumber \]

\[A(L)=80L-2L^{2}\nonumber \]

Esta fórmula representa el área de la barda en términos de la longitud variable$L$.

Comportamiento a corto plazo: Vertex

Ahora exploramos las interesantes características de las gráficas de cuadráticas. Además de las intercepciones, las cuadráticas tienen una característica interesante donde cambian de dirección, llamada vértice. Probablemente notó que todas las cuadráticas están relacionadas con transformaciones de la función cuadrática básica$f(x)=x^{2}$.

Ejemplo$\PageIndex{2}$

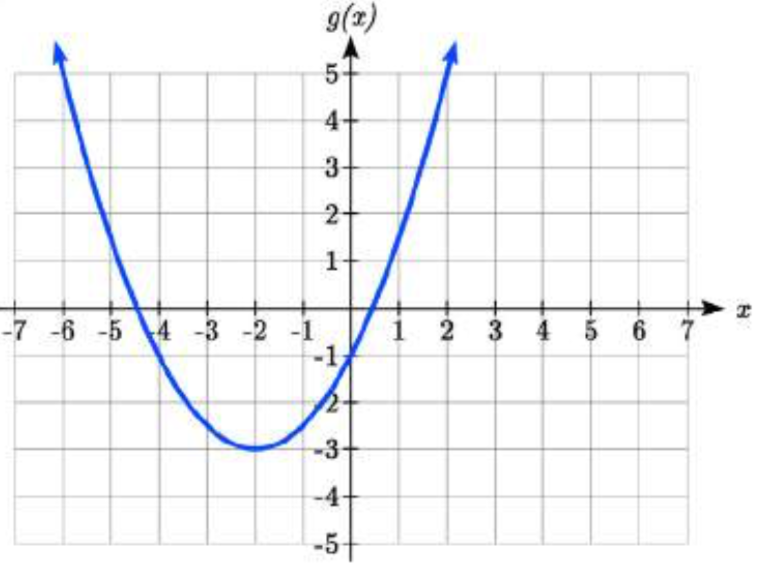
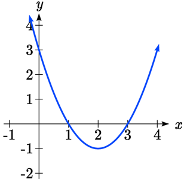
Escriba una ecuación para la cuadrática graficada a continuación como una transformación de$f(x)=x^{2}$, luego expanda la fórmula y simplifique los términos para escribir la ecuación en forma polinomio estándar.

$Parábola en forma de U con vértice en negativo 2 coma negativo 3 y pasando por 0 coma negativo 1.$

Solución

Podemos ver que la gráfica es la cuadrática básica desplazada hacia la izquierda 2 y hacia abajo 3, dando una fórmula en la forma$g(x)=a(x+2)^{2} -3$. Al enchufar un punto que cae sobre la rejilla, como (0, -1), podemos resolver para el factor de estiramiento:

\[\begin{array}{l} {-1=a(0+2)^{2} -3} \\ {2=4a} \\ {a=\dfrac{1}{2} } \end{array}\nonumber \]

Escrita como una transformación, la ecuación para esta fórmula es$g(x)=\dfrac{1}{2} (x+2)^{2} -3$. Para escribir esto en forma polinomio estándar, podemos expandir la fórmula y simplificar términos:

\[\begin{array}{l} {g(x)=\dfrac{1}{2} (x+2)^{2} -3} \\ {g(x)=\dfrac{1}{2} (x+2)(x+2)-3} \\ {g(x)=\dfrac{1}{2} (x^{2} +4x+4)-3} \\ {g(x)=\dfrac{1}{2} x^{2} +2x+2-3} \\ {g(x)=\dfrac{1}{2} x^{2} +2x-1} \end{array}\nonumber \]

Observe que los desplazamientos horizontales y verticales de la cuadrática básica determinan la ubicación del vértice de la parábola; el vértice no se ve afectado por estiramientos y compresiones.

Ejercicio$\PageIndex{1}$

Se ha superpuesto una cuadrícula de coordenadas sobre la trayectoria cuadrática de una básquetbol (Desde http://blog.mrmeyer.com/?p=4778, © Dan Meyer, CC-BY). Encuentra una ecuación para el camino de la pelota. ¿Hace la canasta?

$Imagen en la que se muestra un basquetbol siendo arrojado, con imágenes del basquetbol en varios puntos del camino. Se muestra una cuadrícula sobre la imagen. Usando el punto inferior izquierdo de la gráfica como origen, la canasta se encuentra en 0.5 coma 3.5. El basquetbol se muestra en 8 coma 0, 7.5 coma 2.5, 7 coma 3, 6.5 coma 4, 6 coma 5, 5 coma 6.5 y 4 coma 7.$

Contestar

El camino pasa por el origen con vértice en (-4, 7). \[h(x) = -\dfrac{7}{16}(x + 4)^2 + 7\nonumber\]Para hacer el tiro,$h(-7.5)$ necesitaría ser de aproximadamente 4. $h(-7.5) \approx 1.64$; él no lo logra.

$Una imagen de una básquetbol varios lugares a lo largo de su camino. Se muestra una parábola pasando por la básquetbol, y se le queda corto de la canasta.$

formas de función cuadrática

La forma estándar de una función cuadrática es

\[f(x)=ax^{2} +bx+c \label{standard}\]

La forma de transformación de una función cuadrática es

\[f(x)=a(x-h)^{2} +k \label{trans}\]

El vértice de la función cuadrática se localiza en ($h$,$k$), donde$h$ y$k$ son los números en la forma de transformación de la función. Debido a que el vértice aparece en la forma de transformación, a menudo se le llama la forma de vértice.

En el ejemplo anterior, vimos que es posible reescribir una función cuadrática dada en forma de transformación y reescribirla en forma estándar expandiendo la fórmula. Sería útil revertir este proceso ya que la forma de transformación revela el vértice.

Ampliar la forma de transformación general de una cuadrática da:

\[\begin{array}{l} {f(x)=a(x-h)^{2} +k=a(x-h)(x-h)+k} \\ {f(x)=a(x^{2} -2xh+h^{2} )+k=ax^{2} -2ahx+ah^{2} +k} \end{array}\nonumber \]

Esto debe ser igual a la forma estándar de la cuadrática:

\[ax^{2} -2ahx+ah^{2} +k=ax^{2} +bx+c\nonumber \]

Los términos de segundo grado ya son iguales. Para que los términos lineales sean iguales, los coeficientes deben ser iguales:

\[-2ah=b\text{ ,so }h=-\dfrac{b}{2a}\nonumber\]

Esto nos proporciona un método para determinar el desplazamiento horizontal de la cuadrática a partir de la forma estándar. De igual manera podríamos establecer los términos constantes iguales para encontrar:

\[ah^{2} +k=c\text{ ,so }k=c-ah^{2} =c-a\left(-\dfrac{b}{2a} \right)^{2} =c-a\dfrac{b^{2} }{4a^{2} } =c-\dfrac{b^{2} }{4a}\nonumber \]

En la práctica, sin embargo, suele ser más fácil recordar que$k$ es el valor de salida de la función cuando la entrada es$h$, entonces$k=f(h)$.

encontrar el vértice de una cuadrática

Para una cuadrática dada en forma estándar, el vértice ($h$,$k$) se ubica en:

\[h=-\dfrac{b}{2a} , k=f(h)=f\left(\dfrac{-b}{2a} \right)\]

Ejemplo$\PageIndex{3}$

Encuentra el vértice de la cuadrática$f(x)=2x^{2} -6x+7$. Reescribir la cuadrática en forma de transformación (forma de vértice).

Solución

La coordenada horizontal del vértice estará en

\[h=-\dfrac{b}{2a} =-\dfrac{-6}{2(2)} =\dfrac{6}{4} =\dfrac{3}{2} \nonumber\]

La coordenada vertical del vértice estará en

\[f(\dfrac{3}{2} )=2(\dfrac{3}{2})^{2} -6(\dfrac{3}{2} )+7=\dfrac{5}{2} \nonumber\]

Reescribiendo en forma de transformación, el factor de estiramiento será el mismo que el$a$ en la cuadrática original. Usando el vértice para determinar los desplazamientos,

\[f(x)=2(x-\dfrac{3}{2} )^{2} +\dfrac{5}{2} \nonumber\]

Ejercicio$\PageIndex{2}$

Dada la ecuación$g(x)=13+x^{2} -6x$ escribir la ecuación en forma estándar y luego en forma de transformación/vértice.

Contestar

$g(x) = x^2 - 6x + 13$en forma estándar (Ecuación\ ref {standard}

Encontrar el vértice,$h = \dfrac{-(-6)}{2(1)} = 3$. \[k = g(3) = 3^2 - 6(3) + 13 = 4\nonumber \]

$g(x) = (x - 3)^2 + 4$en forma de transformación (Ecuación\ ref {trans})

Como alternativa al uso de una fórmula para encontrar el vértice, la ecuación también se puede escribir en forma de vértice completando el cuadrado. Este proceso se explica más fácilmente a través del ejemplo. En la mayoría de los casos, usar la fórmula para encontrar el vértice será más rápido y más fácil que completar el cuadrado, pero completar el cuadrado es una técnica útil cuando se enfrentan a algunos otros problemas algebraicos.

Ejemplo$\PageIndex{4}$

Reescribe$f(x)=2x^{2} -12x+14$ en forma de vértice completando el cuadrado.

Solución

Comenzamos por factorizar el coeficiente principal a partir de los términos cuadrático y lineal.

\[2(x^{2} -6x)+14\nonumber \]

A continuación, vamos a agregar algo dentro de los paréntesis para que el cuadrático dentro de los paréntesis se convierta en un cuadrado perfecto. En otras palabras, estamos buscando valores$p$ y$q$ así eso$(x^{2} -6x+p)=(x-q)^{2}$.

Observe que si se multiplica a la derecha, el término medio sería -2q, por lo que q debe ser la mitad del término medio a la izquierda;$q = -3$. En ese caso,$p$ debe ser (-3)${}^{2}$ = 9. \[(x^{2} -6x+9)=(x-3)^{2}\nonumber \]

Ahora bien, no podemos simplemente agregar 9 a la expresión —eso cambiaría el valor de la expresión. De hecho, agregar 9 dentro de los paréntesis en realidad agrega 18 a la expresión, ya que los 2 fuera de los paréntesis se distribuirán. Para mantener equilibrada la expresión, podemos restar 18.

\[2(x^{2} -6x+9)+14-18\nonumber \]

Simplificando, nos quedamos con forma de vértice.

\[2(x-3)^{2} -4\nonumber \]

Además de permitirnos graficar más fácilmente una cuadrática escrita en forma estándar, encontrar el vértice sirve para otro propósito importante: nos permite determinar el valor máximo o mínimo de la función, dependiendo de la forma en que se abra la gráfica.

Ejemplo$\PageIndex{5}$

Regresando a nuestro granjero de patio trasero desde el inicio de la sección, ¿qué dimensiones debería hacer su jardín para maximizar el área cerrada?

Solución

Anteriormente determinamos el área que podía encerrar con 80 pies de esgrima en tres lados estaba dada por la ecuación$A(L)=80L-2L^{2}$. Observe que la cuadrática se ha reflejado verticalmente, ya que el coeficiente sobre el término cuadrado es negativo, por lo que la gráfica se abrirá hacia abajo, y el vértice será un valor máximo para el área.

Al encontrar el vértice, tenemos cuidado ya que la ecuación no está escrita en forma polinómica estándar con potencias decrecientes. Pero sabemos que ese$a$ es el coeficiente sobre el término cuadrado, así$a = -2$,$b = 80$, y$c = 0$.

Encontrar el vértice:

\[h=-\dfrac{80}{2(-2)} =20, k=A(20)=80(20)-2(20)^{2} =800 \nonumber\]

El valor máximo de la función es un área de 800 pies cuadrados, lo que ocurre cuando$L = 20$ los pies. Cuando los lados más cortos son 20 pies, eso deja 40 pies de cercado para el lado más largo. Para maximizar el área, debe encerrar el jardín para que los dos lados más cortos tengan una longitud de 20 pies, y el lado más largo paralelo a la cerca existente tenga una longitud de 40 pies.

Ejemplo$\PageIndex{6}$

Actualmente un periódico local cuenta con 84 mil suscriptores, con un cargo trimestral de 30 dólares. Estudios de mercado han sugerido que si elevaban el precio a 32 dólares perderían 5 mil suscriptores. Suponiendo que las suscripciones están linealmente relacionadas con el precio, ¿qué precio debería cobrar el periódico por una suscripción trimestral para maximizar sus ingresos?

Solución

Los ingresos son la cantidad de dinero que aporta una empresa. En este caso, los ingresos se pueden encontrar multiplicando el cargo por suscripción por el número de suscriptores. Podemos introducir variables,$C$ para cargo por suscripción y S para el número de suscriptores, dándonos la ecuación

\[\text{Revenue} = CS\nonumber\]

Dado que el número de suscriptores cambia con el precio, necesitamos encontrar una relación entre las variables. Sabemos que actualmente$S = 84,000$ y$C = 30$, y que si suben el precio a 32 dólares perderían 5 mil suscriptores, dando un segundo par de valores,$C = 32$ y$S = 79,000$. A partir de esto podemos encontrar una ecuación lineal que relaciona las dos cantidades. Tratando$C$ como la entrada y$S$ como la salida, la ecuación tendrá forma$S=mC+b$. La pendiente será

\[m=\dfrac{79,000-84,000}{32-30} =\dfrac{-5,000}{2} =-2,500\nonumber \]

Esto nos dice que el periódico perderá 2,500 suscriptores por cada dólar que suban el precio. Entonces podemos resolver para la intercepción vertical

\[S=-2500C+b\nonumber\]Enchufe el punto$S = 84,000$ y$C = 30$

\[84,000=-2500(30)+b\nonumber\]Resolver para$b$

\[b=159,000\nonumber\]

Esto nos da la ecuación lineal que$S=-2,500C+159,000$ relaciona costo y suscriptores. Ahora volvemos a nuestra ecuación de ingresos.

\[\text{Revenue} = CS\nonumber\]Sustituir la ecuación por S desde arriba

\[\text{Revenue} = C(-2,500C+159,000)\nonumber\]Ampliando

\[\text{Revenue} = -2,500C^{2} +159,000C\nonumber\]

Ahora tenemos una ecuación cuadrática para los ingresos en función del cargo por suscripción. Para encontrar el precio que maximizará los ingresos para el periódico, podemos encontrar el vértice:

\[h=-\dfrac{159,000}{2(-2,500)} =31.8\nonumber \]

El modelo nos dice que los ingresos máximos se producirán si el periódico cobra 31.80 dólares por una suscripción. Para encontrar cuál es el ingreso máximo, podemos evaluar la ecuación de ingresos:

\[\text{Maximum Revenue} = -2,500(31.8)^{2} +159,000(31.8) = $2,528,100\nonumber\]

Comportamiento a corto plazo: Intercepciones

Como con cualquier función, podemos encontrar las intercepciones verticales de una cuadrática evaluando la función en una entrada de cero, y podemos encontrar las intercepciones horizontales resolviendo para cuándo la salida será cero. Observe que dependiendo de la ubicación de la gráfica, podríamos tener cero, una o dos intercepciones horizontales.

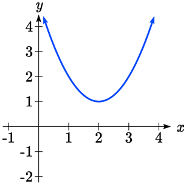
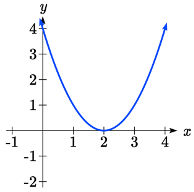
$Parábola en forma de U que se abre hacia arriba con vértice en 2 coma 1 sin intercepciones horizontales.$ $Una parábola en forma de U que se abre hacia arriba con una intercepción horizontal en el vértice en 2 coma 0.$ $Una parábola en forma de U que se abre hacia arriba con vértice a 2 comas negativas 1 con dos intercepciones horizontales en 1 coma 0 y 3 coma 0$

Cero intercepta horizontal una intercepción horizontal dos intercepciones horizontales

Ejemplo$\PageIndex{7}$

Encuentra las intercepciones verticales y horizontales de la cuadrática$f(x)=3x^{2} +5x-2$

Solución

Podemos encontrar la intercepción vertical evaluando la función en una entrada de cero:

\[f(0)=3(0)^{2} +5(0)-2=-2\nonumber\]Intercepción vertical en (0, -2)

Para las intercepciones horizontales, resolvemos para cuando la salida será cero

\[0=3x^{2} +5x-2\nonumber\]

En este caso, la cuadrática se puede factorizar fácilmente, proporcionando el método más simple para la solución

\[0=(3x-1)(x+2)\nonumber\]

\[\begin{array}{l} {0=3x-1} \\ {x=\dfrac{1}{3} } \end{array}\text{ or }\begin{array}{l} {0=x+2} \\ {x=-2} \end{array}\nonumber\]Intercepciones horizontales en$\left(\dfrac{1}{3} ,0\right)$ y (-2,0)

Observe que en la forma estándar de una cuadrática, el término constante c revela la intercepción vertical de la gráfica.

Ejemplo$\PageIndex{8}$

Encuentra las intercepciones horizontales de la cuadrática$f(x)=2x^{2} +4x-4$

Solución

Nuevamente vamos a resolver para cuando la salida será cero

\[0=2x^{2} +4x-4\nonumber\]

Dado que la cuadrática no es fácilmente factorizable en este caso, resolvemos para las intercepciones reescribiendo primero la cuadrática en forma de transformación.

\[h=-\dfrac{b}{2a} =-\dfrac{4}{2(2)} =-1\ \ \ k=f(-1)=2(-1)^{2} +4(-1)-4=-6\nonumber \]

\[f(x)=2(x+1)^{2} -6\nonumber\]

Ahora podemos resolver para cuando la salida será cero

\[\begin{array}{l} {0=2(x+1)^{2} -6} \\ {6=2(x+1)^{2} } \\ {3=(x+1)^{2} } \\ {x+1=\pm \sqrt{3} } \\ {x=-1\pm \sqrt{3} } \end{array}\nonumber \]

La gráfica tiene intercepciones horizontales en$(-1-\sqrt{3} ,0)$ y$(-1+\sqrt{3} ,0)$

Ejercicio$\PageIndex{3}$

En Pruébalo ahora problema 2 encontramos la forma estándar y de transformación para la función$g(x)=13+x^{2} -6x$. Ahora encuentra las intercepciones verticales y horizontales (si las hay).

Contestar: Intercepción vertical en (0, 13), Sin intercepciones horizontales ya que el vértice está por encima del$x$ eje y la gráfica se abre hacia arriba.

El proceso en el último ejemplo se realiza con la suficiente frecuencia que a veces a las personas les resulta más fácil resolver el problema una vez en general y recordar la fórmula del resultado, en lugar de repetir el proceso cada vez. A partir de nuestro trabajo anterior demostramos que cualquier cuadrática en forma estándar puede escribirse en forma de transformación como:

\[f(x)=a(x+\dfrac{b}{2a} )^{2} +c-\dfrac{b^{2} }{4a}\]

Resolver para las intercepciones horizontales usando esta ecuación general da:

\[0=a(x+\dfrac{b}{2a} )^{2} +c-\dfrac{b^{2} }{4a}\nonumber\]empezar a resolver$x$ moviendo las constantes hacia el otro lado

\[\dfrac{b^{2} }{4a} -c=a(x+\dfrac{b}{2a} )^{2}\nonumber \]dividir ambos lados por$a$

\[\dfrac{b^{2} }{4a^{2} } -\dfrac{c}{a} = (x+\dfrac{b}{2a})^{2}\nonumber \]encontrar un denominador común para combinar fracciones

\[\dfrac{b^{2} }{4a^{2} } -\dfrac{4ac}{4a^{2} } =\left(x+\dfrac{b}{2a} \right)^{2}\nonumber \]combinar las fracciones en el lado izquierdo de la ecuación

\[\dfrac{b^{2} -4ac}{4a^{2} } =\left(x+\dfrac{b}{2a} \right)^{2}\nonumber \]tomar la raíz cuadrada de ambos lados

\[\pm \sqrt{\dfrac{b^{2} -4ac}{4a^{2} } } =x+\dfrac{b}{2a}\nonumber\]restar$b/2a$ de ambos lados

\[-\dfrac{b}{2a} \pm \dfrac{\sqrt{b^{2} -4ac} }{2a} =x\nonumber \]combinar las fracciones

\[x=\dfrac{-b\pm \sqrt{b^{2} -4ac} }{2a}\nonumber \]Observe que esto puede arrojar dos respuestas diferentes para$x$

Fórmula cuadrática

Para una función cuadrática dada en forma estándar$f(x)=ax^{2} +bx+c$, la fórmula cuadrática da las intercepciones horizontales de la gráfica de esta función.

\[x=\dfrac{-b\pm \sqrt{b^{2} -4ac} }{2a}\]

Ejemplo$\PageIndex{9}$

Se lanza una pelota hacia arriba desde lo alto de un edificio de 40 pies de altura a una velocidad de 80 pies por segundo. La altura de la pelota sobre el suelo puede ser modelada por la ecuación$H(t)=-16t^{2} +80t+40$.

¿Cuál es la altura máxima de la pelota?

¿Cuándo choca la pelota contra el suelo?

Solución

Para encontrar la altura máxima de la pelota, necesitaríamos conocer el vértice de la cuadrática.

\[h=-\dfrac{80}{2(-16)} =\dfrac{80}{32} =\dfrac{5}{2} , k=H\left(\dfrac{5}{2} \right)=-16\left(\dfrac{5}{2} \right)^{2} +80\left(\dfrac{5}{2} \right)+40=140\nonumber \]

El balón alcanza una altura máxima de 140 pies después de 2.5 segundos.

Para saber cuándo la pelota golpea el suelo, necesitamos determinar cuándo la altura es cero, cuándo$H(t) = 0$. Si bien podríamos hacer esto usando la forma de transformación de la cuadrática, también podemos usar la fórmula cuadrática:

\[t=\dfrac{-80\pm \sqrt{80^{2} -4(-16)(40)} }{2(-16)} =\dfrac{-80\pm \sqrt{8960} }{-32}\nonumber \]

Como la raíz cuadrada no simplifica muy bien, podemos usar una calculadora para aproximar los valores de las soluciones:

\[t=\dfrac{-80-\sqrt{8960} }{-32} \approx 5.458\text{ or }t=\dfrac{-80+\sqrt{8960} }{-32} \approx -0.458\nonumber \]

La segunda respuesta está fuera del dominio razonable de nuestro modelo, por lo que concluimos que la pelota golpeará el suelo después de aproximadamente 5.458 segundos.

Ejercicio$\PageIndex{4}$

Para estas dos ecuaciones determinar si el vértice será un valor máximo o un valor mínimo.

$g(x)=-8x+x^{2} +7$
$g(x)=-3(3-x)^{2} +2$

Contestar

a. El vértice es un valor mínimo, ya que$a > 0$ y la gráfica se abre hacia arriba

b. El vértice es un valor máximo, ya que$a < 0$ y la gráfica se abre hacia abajo

Temas Importantes de esta Sección

Funciones cuadráticas
Forma estándar
Forma de transformación/forma de vértice
Vértice como máximo/Vértice como mínimo
Comportamiento a corto plazo
Intercepciones Vertex/Horizontales y Verticales
Fórmula cuadrática