3.3: Gráficas de Funciones Polinómicas

Última actualización
Guardar como PDF

Page ID: 116411

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la sección anterior, exploramos el comportamiento a corto plazo de las cuadráticas, un caso especial de polinomios. En esta sección, exploraremos el comportamiento a corto plazo de polinomios en general.

Comportamiento a corto plazo: Intercepciones

Como con cualquier función, la intercepción vertical se puede encontrar evaluando la función a una entrada de cero. Al tratarse de una evaluación, es relativamente fácil hacerlo para un polinomio de cualquier grado.

Para encontrar intercepciones horizontales, necesitamos resolver para cuándo la salida será cero. Para los polinomios generales, esta puede ser una perspectiva desafiante. Si bien las cuadráticas se pueden resolver usando la fórmula cuadrática relativamente simple, las fórmulas correspondientes para polinomios cúbicos y de 4${}^{th}$ grados no son lo suficientemente simples como para recordar, y las fórmulas no existen para polinomios generales de grado superior. En consecuencia, nos limitaremos a tres casos:

El polinomio se puede factorizar utilizando métodos conocidos: mayor factor común y factorización trinomial.
El polinomio se da en forma factorizada.
La tecnología se utiliza para determinar las intercepciones.

Otras técnicas para encontrar las intercepciones de polinomios generales se explorarán en la siguiente sección.

Ejemplo$\PageIndex{1}$

Encuentra las intercepciones horizontales de$f(x)=x^{6} -3x^{4} +2x^{2}$.

Solución

Podemos intentar factorizar este polinomio para encontrar soluciones para$f(x) = 0$.

\[x^{6} -3x^{4} +2x^{2} =0\nonumber \]Factorizando el mayor factor común

\[x^{2} (x^{4} -3x^{2} +2)=0\nonumber \]Factorizar el interior como cuadrático en x${}^{2}$

\[x^{2} (x^{2} -1)(x^{2} -2)=0\nonumber \]Luego descomponerse para encontrar soluciones

\[\begin{array}{l} {x^{2} =0} \\ {x=0} \end{array}\text{ or }\begin{array}{l} {\left(x^{2} -1\right)=0} \\ {x^{2} =1} \\ {x=\pm 1} \end{array}\text{ or }\begin{array}{l} {\left(x^{2} -2\right)=0} \\ {x^{2} =2} \\ {x=\pm \sqrt{2} } \end{array}\nonumber \]

Esto nos da 5 intercepciones horizontales.

Ejemplo$\PageIndex{2}$

Encuentra las intercepciones verticales y horizontales de$g(t)=(t-2)^{2} (2t+3)$

Solución

La intercepción vertical se puede encontrar evaluando$g(0)$.

\[g(0)=(0-2)^{2} (2(0)+3)=12\nonumber \]

Las intercepciones horizontales se pueden encontrar resolviendo$g(t) = 0$

\[(t-2)^{2} (2t+3)=0\nonumber\]Como esto ya está factorizado, podemos separarlo:

\[\begin{array}{l} {(t-2)^{2} =0} \\ {t-2=0} \\ {t=2} \end{array}\text{ or }\begin{array}{l} {(2t+3)=0} \\ {t=\dfrac{-3}{2} } \end{array}\nonumber \]

Siempre podemos verificar que nuestras respuestas son razonables graficando el polinomio.

Ejemplo$\PageIndex{3}$

Encuentra las intercepciones horizontales de$h(t)=t^{3} +4t^{2} +t-6$

Solución

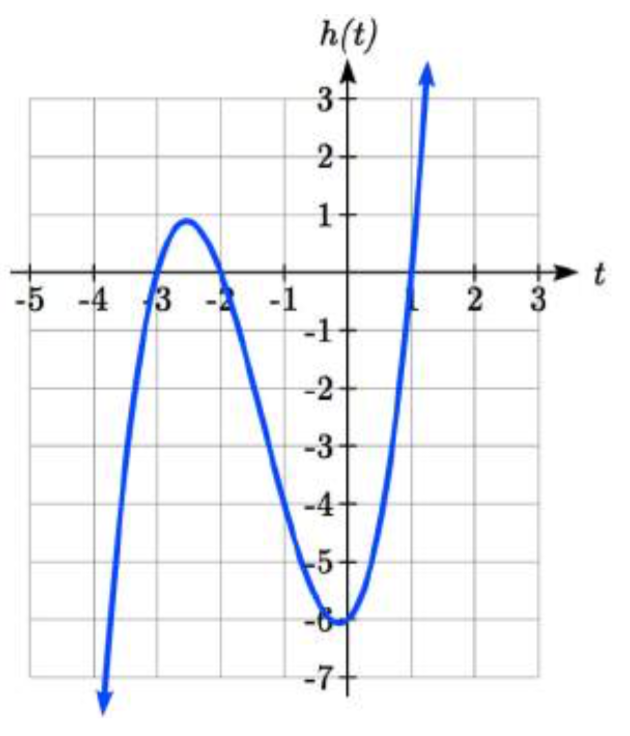$Un polinomio que aumenta, disminuye, luego aumenta, con intercepciones horizontales aparentes en negativo 3 coma 0, negativo 2 coma 0 y 1 coma 0$ Dado que este polinomio no está en forma factorizada, no tiene factores comunes y no parece ser factorizable utilizando técnicas que conocemos, podemos recurrir a la tecnología para encontrar las intercepciones.

Graficando esta función, parece que hay intercepciones horizontales en$t$ = -3, -2 y 1.

Podríamos verificar que estos sean correctos enchufando estos valores para t y verificando eso$h(-3)=h(-2)=h(1)=0$.

Ejercicio$\PageIndex{1}$

Encuentra las intercepciones verticales y horizontales de la función$f(t)=t^{4} -4t^{2}$.

Responder: Intercepción vertical (0, 0). $0=t^{4} -4t^{2}$factores como Intercepciones$0=t^{2} \left(t^{2} -4\right)=t^{2} \left(t-2\right)\left(t+2\right)$ horizontales (0, 0), (-2, 0), (2, 0).

Comportamiento gráfico en las intercepciones 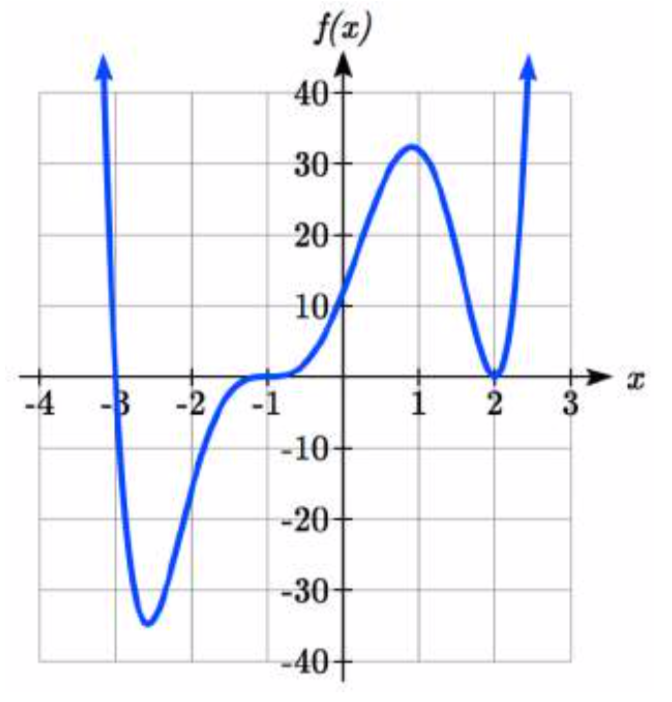$Un polinomio que disminuye pasando por negativo 3 coma 0 bajando a aproximadamente negativo 2.5 coma negativo 33 luego aumentando pero aplanándose en negativo 1 coma 0 en el camino hasta aproximadamente 0.9 coma 32, luego disminuyendo a 2 coma 0, luego aumentando nuevamente.$

Si graficamos la función$f(x)=(x+3)(x-2)^{2} (x+1)^{3}$, observe que el comportamiento en cada una de las intercepciones horizontales es diferente.

En la intercepción horizontal x = -3, proveniente del$(x+3)$ factor del polinomio, la gráfica pasa directamente a través de la intercepción horizontal.

El factor$(x+3)$ es lineal (tiene una potencia de 1), por lo que el comportamiento cerca de la intercepción es como el de una línea - pasa directamente a través de la intercepción. A esto lo llamamos un solo cero, ya que el cero corresponde a un solo factor de la función.

En la intercepción horizontal$x = 2$, proveniente del$(x-2)^{2}$ factor del polinomio, la gráfica toca el eje en la intercepción y cambia de dirección. El factor es cuadrático (grado 2), por lo que el comportamiento cerca de la intercepción es como el de un cuadrático, rebota en el eje horizontal en la intercepción. Ya que$(x-2)^{2} =(x-2)(x-2)$, el factor se repite dos veces, por lo que llamamos a esto un doble cero. También podríamos decir que el cero tiene multiplicidad 2.

En la intercepción horizontal$x = -1$, proveniente del$(x+1)^{3}$ factor del polinomio, la gráfica pasa por el eje en la intercepción, pero primero se aplana un poco. Este factor es cúbico (grado 3), por lo que el comportamiento cerca de la intercepción es como el de un cúbico, con la misma forma de tipo “S” cerca de la intercepción que$x^{3}$ tiene el kit de herramientas. A esto lo llamamos un triple cero. También podríamos decir que el cero tiene multiplicidad 3.

Al utilizar estos comportamientos, podemos esbozar una gráfica razonable de una función polinómica factorizada sin necesidad de tecnología.

comportamiento gráfico de polinomios en intercepciones horizontales

Si un polinomio contiene un factor de la forma$(x-h)^{p}$, el comportamiento cerca de la intercepción horizontal$h$ está determinado por la potencia en el factor.

$p = 1$$p = 2$$p = 3$

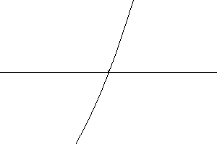
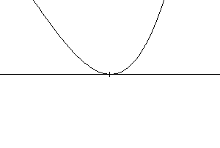
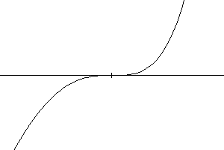
$clipboard_ef72e249454eda647a2fe5334d03cc65a.png$ $clipboard_e3e1bb574497201c17bf9239841368729.png$ $clipboard_eec85ccd73425c617162dab3843761510.png$

Multiplicidad Cero Simple 1 Doble Multiplicidad Cero 2 Multiplicidad Triple Cero 3

Para potencias pares superiores 4,6,8 etc.... la gráfica aún rebotará en el eje horizontal pero la gráfica aparecerá más plana con cada vez que aumenta la potencia par a medida que se acerca y sale del eje.

Para potencias impares superiores, 5,7,9 etc... la gráfica seguirá pasando por el eje horizontal pero la gráfica aparecerá más plana con cada potencia impar creciente a medida que se acerca y abandone el eje.

Ejemplo$\PageIndex{4}$

Esbozar una gráfica de$f(x)=-2(x+3)^{2} (x-5)$.

Solución

Esta gráfica tiene dos intercepciones horizontales. At$x = -3$, el factor es cuadrado, lo que indica que la gráfica rebotará en esta intercepción horizontal. At$x = 5$, el factor no es cuadrado, lo que indica que la gráfica pasará por el eje en esta intercepción.

Adicionalmente, podemos ver el término principal, si este polinomio se multiplicara, sería$-2x^{3}$, por lo que el comportamiento a largo plazo es el de un cúbico reflejado verticalmente, con las salidas disminuyendo a medida que las entradas obtienen grandes positivos, y las entradas aumentando a medida que las entradas se vuelven grandes negativas.

Para bosquejar esto consideramos lo siguiente: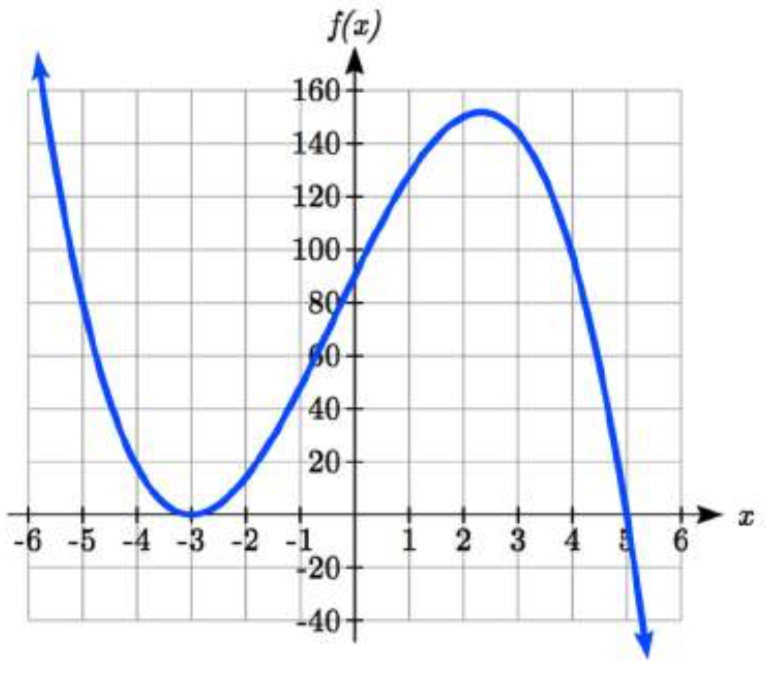 $Una gráfica que disminuye a negativo 3 coma 0 luego aumenta a través de 0 coma 90 y continúa hasta aproximadamente 2.1 coma 150, luego decae pasando por 5 coma 0$

Como$x \to -\infty$ la función$f(x) \to \infty$ así conocemos la gráfica comienza en el${}^{nd}$ cuadrante 2 y va disminuyendo hacia el eje horizontal.

En (-3, 0) la gráfica rebota en el eje horizontal y así la función debe comenzar a aumentar.

En (0, 90) la gráfica cruza el eje vertical en la intercepción vertical.

En algún lugar después de este punto, la gráfica debe volver a bajar o comenzar a disminuir hacia el eje horizontal ya que la gráfica pasa por la siguiente intercepción en (5,0).

Como$x \to \infty$ la función$f(x) \to -\infty$ así conocemos la gráfica sigue disminuyendo y podemos dejar de dibujar la gráfica en el${}^{th}$ cuadrante 4.

Utilizando la tecnología podemos verificar la forma de la gráfica.

Ejercicio$\PageIndex{2}$

Dada la función$g(x)=x^{3} -x^{2} -6x$ utilizamos los métodos que hemos aprendido hasta ahora para encontrar las intercepciones verticales y horizontales, determinar dónde la función es negativa y positiva, describir el comportamiento a largo plazo y bosquejar la gráfica sin tecnología.

Responder

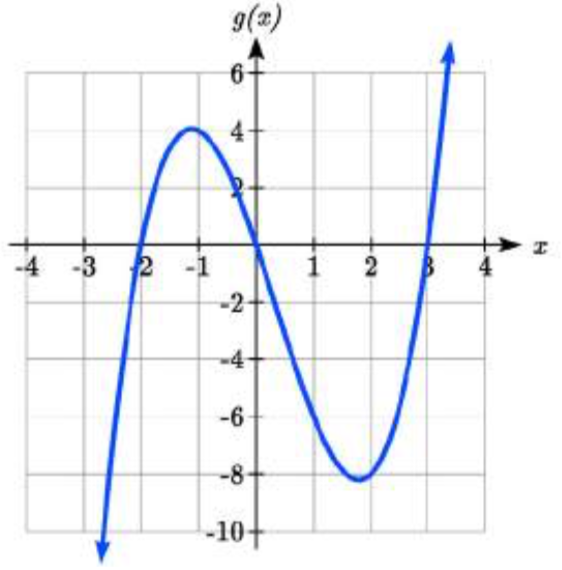$Un gráfico que aumenta pasando por negativo 2 coma 0 hasta aproximadamente negativo 1 coma 4, luego disminuye pasando por 0 coma 0 hasta aproximadamente 1.7 coma negativa 8 luego aumenta pasando por 3 coma 0$ Intercepción vertical (0, 0), Intercepciones horizontales (-2, 0), (0, 0), (3, 0)

La función es negativa en ($-\infty$, -2) y (0, 3)

La función es positiva en (-2, 0) y (3,$\infty$)

El término principal es$x^{3}$ así como$x\to -\infty$,$g(x)\to -\infty$ y como$x\to \infty$,$g(x)\to \infty$

Resolviendo Desigualdades Polinómicas

Una aplicación de nuestra capacidad para encontrar intercepciones y esbozar un gráfico de polinomios es la capacidad de resolver desigualdades polinómicas. Es una pregunta muy común preguntarse cuándo una función será positiva y negativa. Podemos resolver desigualdades polinomiales ya sea utilizando la gráfica, o usando valores de prueba.

Ejemplo$\PageIndex{5}$

Resolver$(x+3)(x+1)^{2} (x-4)>0$

Solución

Al igual que con todas las desigualdades, comenzamos por resolver la igualdad$(x+3)(x+1)^{2} (x-4)=0$, que tiene soluciones en x = -3, -1 y 4. Sabemos que la función solo puede cambiar de positivo a negativo en estos valores, por lo que estos dividen las entradas en 4 intervalos.

Podríamos elegir un valor de prueba en cada intervalo y evaluar la función$f(x)=(x+3)(x+1)^{2} (x-4)$ en cada valor de prueba para determinar si la función es positiva o negativa en ese intervalo

Intervalo	Prueba$x$ en intervalo	$f$(valor de prueba)	> 0 o < 0?
$x < -3$	\ (x\) en intervalo” style="vertical-align:middle; ">-4	\ (f\) (valor de prueba)” style="vertical-align:middle; ">72	0 or < 0?" style="vertical-align:middle;">> 0
$-3 < x < -1$	\ (x\) en intervalo” style="vertical-align:middle; ">-2	\ (f\) (valor de prueba)” style="vertical-align:middle; ">-6	0 or < 0?" style="vertical-align:middle;">< 0
$-1 < x < 4$	\ (x\) en intervalo” style="vertical-align:middle; ">0	\ (f\) (valor de prueba)” style="vertical-align:middle; ">-12	0 or < 0?" style="vertical-align:middle;">< 0
$x > 4$	\ (x\) en intervalo” style="vertical-align:middle; ">5	\ (f\) (valor de prueba)” style="vertical-align:middle; ">288	0 or < 0?" style="vertical-align:middle;">> 0

En una línea numérica esto se vería así:

$Una línea numérica dividida en 4 segmentos. El segmento a la izquierda de -3 está etiquetado como positivo. El segmento de -3 a -1 está etiquetado como negativo. El segmento de -1 a 4 se etiqueta negativo. El segmento a la derecha de 4 está etiquetado como positivo.$

A partir de nuestros valores de prueba, podemos determinar que esta función es positiva cuando$x < -3$ o$x > 4$, o en notación de intervalo,$(-\infty ,-3)\bigcup (4,\infty )$

También podríamos haber determinado en qué intervalos la función era positiva dibujando una gráfica de la función. Ilustramos esa técnica en el siguiente ejemplo

Ejemplo$\PageIndex{6}$

Encuentra el dominio de la función$v(t)=\sqrt{6-5t-t^{2} }$.

Solución

Una raíz cuadrada solo se define cuando la cantidad de la que estamos tomando la raíz cuadrada, la cantidad dentro de la raíz cuadrada, es cero o mayor. Así, el dominio de esta función será cuándo$6-5t-t^{2} \ge 0$.

Empezamos por resolver la igualdad$6-5t-t^{2} =0$. Si bien podríamos usar la fórmula cuadrática, esta ecuación tiene muy buenos factores para$(6+t)(1-t)=0$, dando intercepciones horizontales$t = 1$ y$t = -6$.

Dibujar una gráfica de esta cuadrática nos permitirá determinar cuándo es positiva. 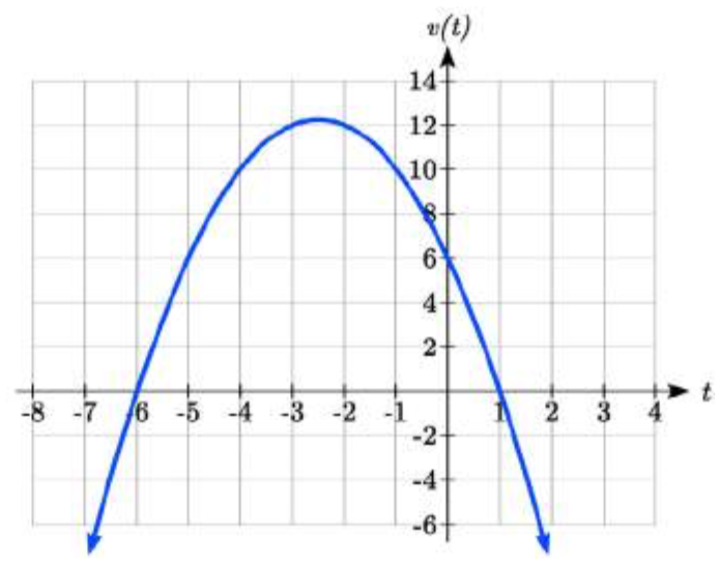$Una parábola en forma de U de apertura hacia abajo con intercepciones horizontales en negativo 6 coma 0 y 1 coma 0$

De la gráfica podemos ver que esta función es positiva para entradas entre las intercepciones. Entonces$6 - 5t - t^{2} \ge 0$ para$-6 \le t \le 1$, y este será el dominio de la$v(t)$ función.

Escribir ecuaciones usando intercepciones

Dado que una función polinómica escrita en forma factorizada tendrá una intercepción horizontal donde cada factor es igual a cero, podemos formar una función que pasará por un conjunto de intercepciones horizontales introduciendo un conjunto de factores correspondientes.

forma factorizada de polinomios

Si un polinomio tiene intercepciones horizontales en$x=x_{1} ,x_{2} , ... ,x_{n}$, entonces el polinomio se puede escribir en forma factorizada

\[f(x)=a(x-x_{1} )^{p_{1} } (x-x_{2} )^{p_{2} } \cdots (x-x_{n} )^{p_{n} }\]

donde$p_i$ las potencias de cada factor pueden ser determinadas por el comportamiento de la gráfica en la intercepción correspondiente, y el factor de estiramiento a puede determinarse dado un valor de la función distinto de la intercepción horizontal.

Ejemplo$\PageIndex{7}$

Escribe una fórmula para la función polinómica graficada aquí.

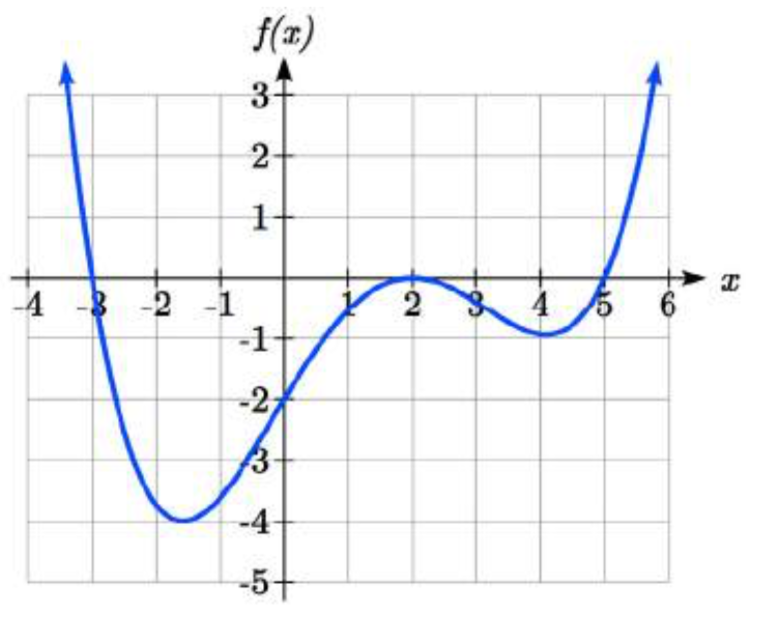
$Un polinomio que disminuye pasando por negativo 3 coma 0, luego aumenta pasando por 0 coma negativa 2 hasta 2 coma 0, luego disminuye a aproximadamente 4 coma negativa 1 luego aumenta pasando por 5 coma 0$

Solución

Esta gráfica tiene tres intercepciones horizontales:$x$ = -3, 2 y 5. At$x$ = -3 y 5 la gráfica pasa por el eje, sugiriendo que los factores correspondientes del polinomio serán lineales. En$x = 2$ la gráfica rebota en la intercepción, sugiriendo que el factor correspondiente del polinomio será de 2${}^{nd}$ grados (cuadrático).

Juntos, esto nos da:

\[f(x)=a(x+3)(x-2)^{2} (x-5)\nonumber \]

Para determinar el factor de estiramiento, podemos utilizar otro punto en la gráfica. Aquí, la intercepción vertical parece ser (0, -2), por lo que podemos enchufar esos valores para resolver para$a$:

\[\begin{array}{l} {-2=a(0+3)(0-2)^{2} (0-5)} \\ {-2=-60a} \\ {a=\dfrac{1}{30} } \end{array}\nonumber \]

El polinomio graficado parece representar la función

\[f(x)=\dfrac{1}{30} (x+3)(x-2)^{2} (x-5)\nonumber\]

Ejercicio$\PageIndex{3}$

Dada la gráfica, escriba una fórmula para la función mostrada.

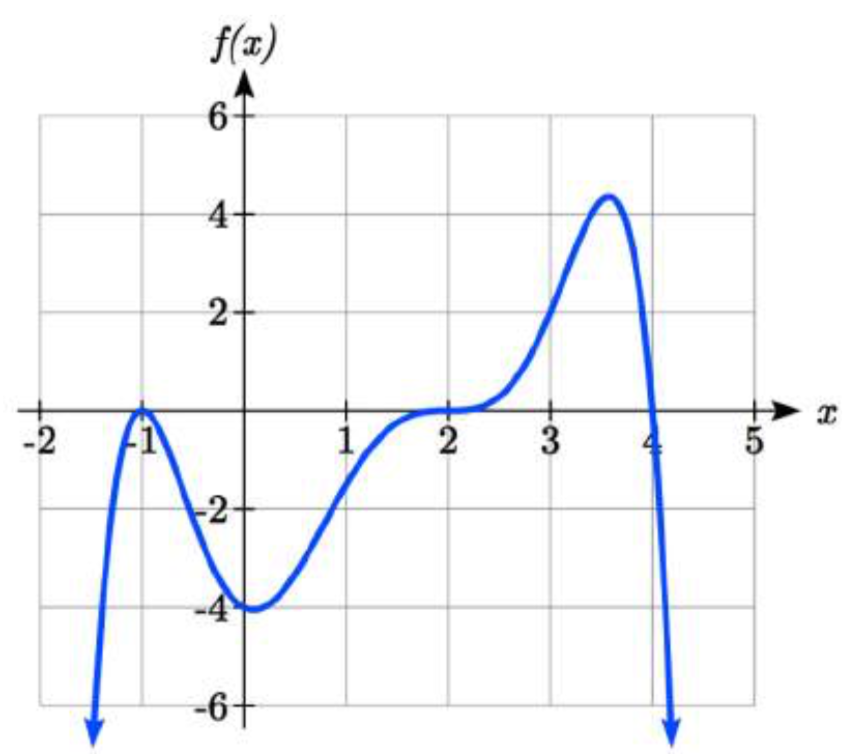
$Un polinomio que aumenta a negativo 1 coma 0, disminuye a 0 coma negativa 4, aumenta hasta 2 coma 0 nivelando en esa intercepción, los aumentos más antes de disminuir pasando por 4 coma 0$

Responder: Doble cero at$x= - 1$, triple cero at$x = 2$. Solo cero en$x = 4$. $f(x) = a(x - 2)^{3} (x+1)^{2} (x-4)$. Sustituir (0, -4) y resolver$a$,$f(x) = -\dfrac{1}{8} (x-2)^{3} (x+1)^{2} (x-4)$

Estimando Extrema

Con cuadráticas, pudimos encontrar algebraicamente el valor máximo o mínimo de la función al encontrar el vértice. Para polinomios generales, encontrar estos puntos de inflexión no es posible sin técnicas más avanzadas del cálculo. Incluso entonces, encontrar dónde ocurren los extremos aún puede ser un desafío algebraico. Por ahora, estimaremos las ubicaciones de los puntos de inflexión utilizando la tecnología para generar una gráfica.

Ejemplo$\PageIndex{8}$

Se construirá una caja abierta cortando cuadrados de cada esquina de una lámina de plástico de 14 cm por 20 cm y luego doblando los lados. Encuentra el tamaño de los cuadrados que deben recortarse para maximizar el volumen encerrado por la caja.

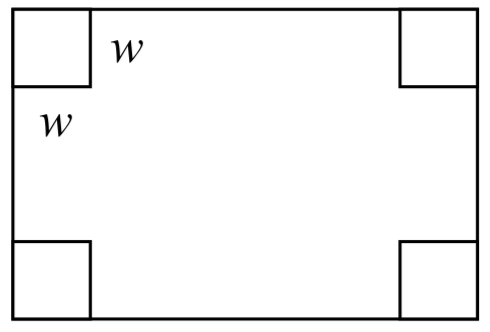
$Un rectángulo grande con cuadrados en cada esquina. Los lados de los cuadrados están etiquetados con w.$

Solución

Comenzaremos este problema dibujando una imagen, etiquetando el ancho de los cuadrados recortados con una variable,$w$.

Observe que después de cortar un cuadrado de cada extremo, deja un rectángulo$(14-2w)$ cm por$(120-2w)$ cm para la base de la caja, y la caja tendrá$w$ cm de altura. Esto da el volumen:

\[V(w)=(14-2w)(20-2w)w=280w-68w^{2} +4w^{3}\nonumber\]

El uso de la tecnología para esbozar una gráfica nos permite estimar el valor máximo para el volumen, restringido a valores razonables para$w$: valores de 0 a 7.

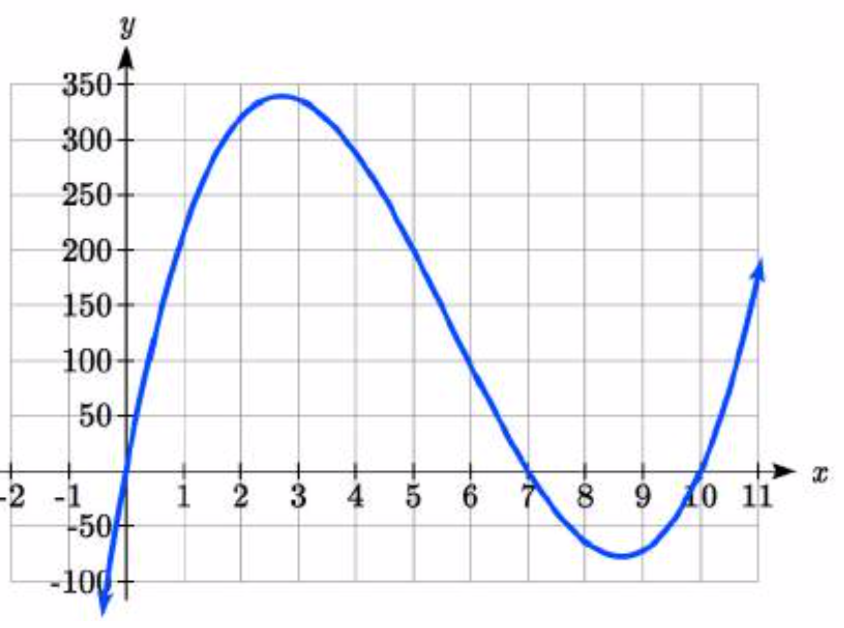
$Un polinomio que aumenta pasando por 0 coma 0 hasta aproximadamente 2.4 coma 340, luego disminuye pasando por 7 coma 0, luego aumenta pasando por 10 coma 0$

A partir de esta gráfica, podemos estimar que el valor máximo es alrededor de 340, y ocurre cuando los cuadrados son aproximadamente 2.75cm cuadrados. Para mejorar esta estimación, podríamos usar funciones avanzadas de nuestra tecnología, si están disponibles, o simplemente cambiar nuestra ventana para acercar nuestra gráfica.

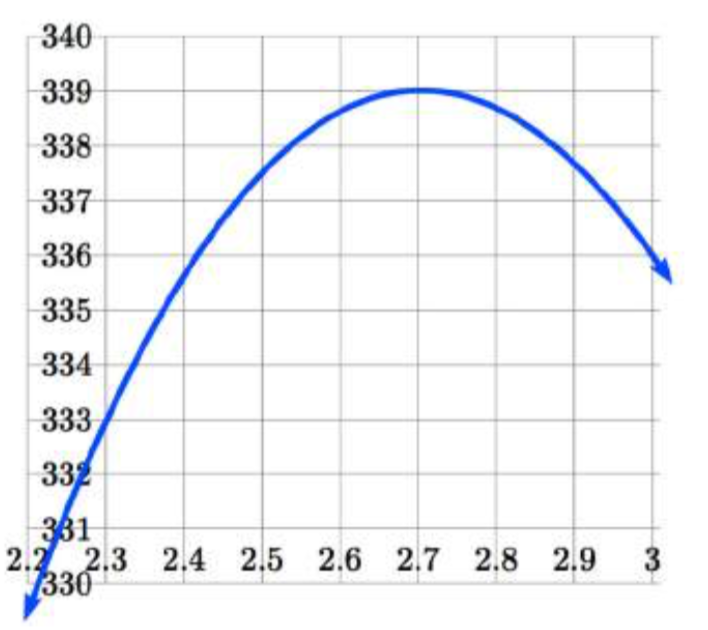
$Una gráfica con zoom con escala horizontal de 2.3 a 3 en pasos de 0.1 y escala vertical de 331 a 340. Una gráfica en forma de U de apertura hacia abajo con un máximo de alrededor de 2.7 coma 339$

Desde esta vista ampliada, podemos refinar nuestra estimación para el volumen máximo a aproximadamente 339, cuando los cuadrados son de 2.7cm cuadrados.

Ejercicio$\PageIndex{4}$

Utilice la tecnología para encontrar los valores máximo y mínimo en el intervalo [-1, 4] de la función$f(x)=-0.2(x-2)^{3} (x+1)^{2} (x-4)$.

Responder: El mínimo ocurre aproximadamente en el punto (0, -6.5), y el máximo ocurre aproximadamente en el punto (3.5, 7).

Temas Importantes de esta Sección

Comportamiento a corto plazo
Intercepciones (Horizontales y Verticales)
Métodos para encontrar intercepciones horizontales
Métodos de Factoring
Formularios factorizados
Tecnología
Comportamiento gráfico en las intercepciones
Ceros simples, dobles y triples (o multiplicidad de comportamientos 1, 2 y 3)
Resolver desigualdades polinomiales usando valores de prueba y técnicas de gráficos
Escribir ecuaciones usando intercepciones
Estimando extrema

Intervalo	Prueba\(x\) en intervalo	\(f\)(valor de prueba)	> 0 o < 0?
\(x < -3\)	\ (x\) en intervalo” style="vertical-align:middle; ">-4	\ (f\) (valor de prueba)” style="vertical-align:middle; ">72	0 or < 0?" style="vertical-align:middle;">> 0
\(-3 < x < -1\)	\ (x\) en intervalo” style="vertical-align:middle; ">-2	\ (f\) (valor de prueba)” style="vertical-align:middle; ">-6	0 or < 0?" style="vertical-align:middle;">< 0
\(-1 < x < 4\)	\ (x\) en intervalo” style="vertical-align:middle; ">0	\ (f\) (valor de prueba)” style="vertical-align:middle; ">-12	0 or < 0?" style="vertical-align:middle;">< 0
\(x > 4\)	\ (x\) en intervalo” style="vertical-align:middle; ">5	\ (f\) (valor de prueba)” style="vertical-align:middle; ">288	0 or < 0?" style="vertical-align:middle;">> 0