3.8: Funciones inversas y radicales

Última actualización
Guardar como PDF

Page ID: 116489

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, exploraremos los inversos de las funciones polinomiales y racionales, y en particular las funciones radicales que surgen en el proceso.

Ejemplo$\PageIndex{1}$

Un colector de escorrentía de agua está construido en forma de un cilindroparabólico como se muestra a continuación. Encontrar la superficie del agua en el canal como una función de la profundidad del agua.

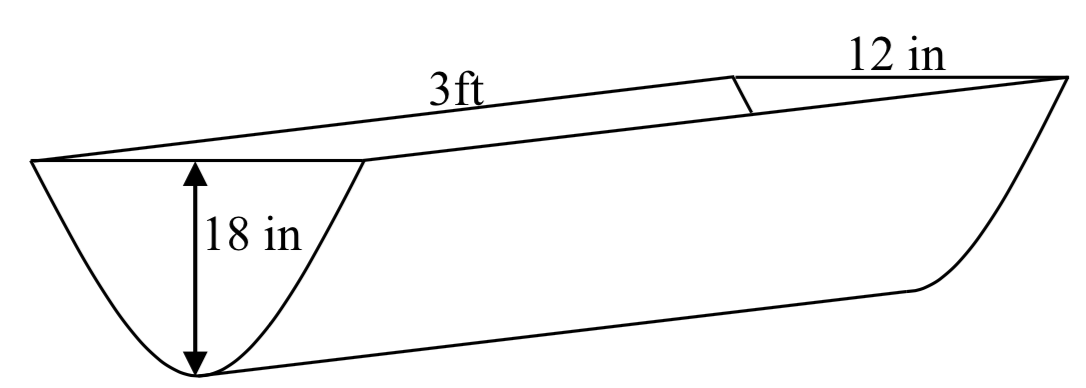
$Un cilindroparabólico, donde la cara frontal tiene la forma de parte de una parábola en forma de U que mide 18 pulgadas de alto y 12 pulgadas de ancho en la parte superior, y los lados del canal se extienden rectos hacia atrás 3 pies.$

Solución

Dado que será útil tener una ecuación para la forma de la sección transversal parabólica, impondremos un sistema de coordenadas en la sección transversal, con$x$ medidas horizontalmente y$y$ medidas verticalmente, con el origen en el vértice de la parábola.

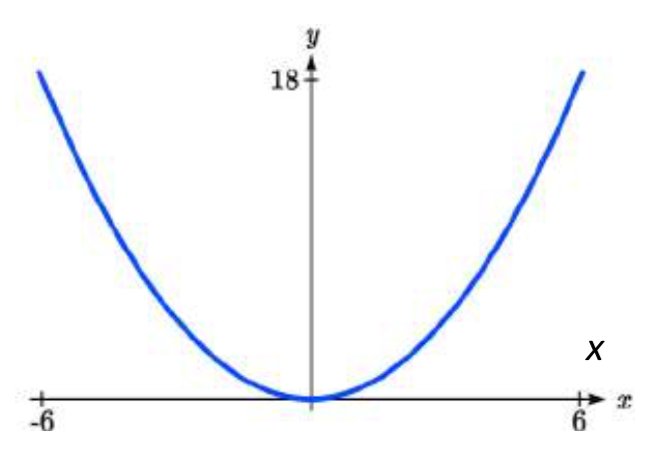
$Parábola en forma de U con vértice en el origen y pasando por los puntos negativos 6 coma 18 y 6 coma 18.$

De esto encontramos una ecuación para la forma parabólica. Ya que colocamos el origen en el vértice de la parábola, sabemos que la ecuación tendrá forma$y(x)=ax^{2}$. Nuestra ecuación tendrá que pasar por el punto (6,18), a partir del cual podemos resolver para el factor de estiramiento$a$:

\[\begin{array}{l} {18=a6^{2} } \\ {a=\dfrac{18}{36} =\dfrac{1}{2} } \end{array}\nonumber \]

Nuestra sección transversal parabólica tiene ecuación$y(x)=\dfrac{1}{2} x^{2}$

Dado que estamos interesados en la superficie del agua, nos interesa determinar el ancho en la parte superior del agua en función de la profundidad del agua. Para cualquier profundidad$y$ el ancho estará dado por$2x$, por lo que necesitamos resolver la ecuación anterior para$x$. Sin embargo, observe que la función original no es uno a uno, y de hecho dado cualquier salida hay dos entradas que producen la misma salida, una positiva y otra negativa.

Para encontrar una inversa, podemos restringir nuestra función original a un dominio limitado en el que es uno a uno. En este caso, tiene sentido restringirnos a valores x positivos. En este dominio, podemos encontrar una inversa resolviendo para la variable de entrada:

\[\begin{array}{l} {y=\dfrac{1}{2} x^{2} } \\ {2y=x^{2} } \end{array}\quad x=\pm \sqrt{2y}\nonumber \]

Esta no es una función como está escrita. Como nos estamos limitando a$x$ valores positivos, eliminamos la solución negativa, dándonos la función inversa que estamos buscando

\[x(y)=\sqrt{2y}\nonumber \]

Ya que$x$ mide desde el centro hacia afuera, todo el ancho del agua en la parte superior será$2x$. Dado que el canal tiene 3 pies (36 pulgadas) de largo, el área de superficie será entonces 36 (2x), o en términos de$y$:

\[\text{Area}=72x=72\sqrt{2y}\nonumber\]

El ejemplo anterior ilustraba dos cosas importantes:

Al encontrar la inversa de una cuadrática, tenemos que limitarnos a un dominio en el que la función es uno a uno.
La inversa de una función cuadrática es una función de raíz cuadrada. Ambas son funciones de kit de herramientas y diferentes tipos de funciones de potencia.

Las funciones que involucran raíces a menudo se denominan funciones radicales.

Ejemplo$\PageIndex{2}$

Encuentra la inversa de$f(x)=(x-2)^{2} -3=x^{2} -4x+1$

Solución

A partir de la forma de transformación de la función, podemos ver que esta es una cuadrática transformada con vértice en (2, -3) que se abre hacia arriba. Dado que la gráfica estará disminuyendo en un lado del vértice, y aumentando en el otro lado, podemos restringir esta función a un dominio en el que será uno a uno limitando el dominio a$x \ge 2$.

Para encontrar la inversa, usaremos la forma de vértice de la cuadrática. Comenzamos reemplazando el$f(x)$ por una variable simple$y$, luego resolvemos para$x$.

\[y=(x-2)^{2} -3\nonumber\]Agregar 3 a ambos lados

\[y+3=(x-2)^{2}\nonumber\]Toma la raíz cuadrada

\[\pm \sqrt{y+3} =x-2\nonumber\]Agregar 2 a ambos lados

\[2\pm \sqrt{y+3} =x\nonumber \]

Por supuesto, tal como está escrito esto no es una función. Dado que restringimos nuestra función original a un dominio de$x\ge 2$, las salidas de la inversa deberían ser las mismas, diciéndonos que utilicemos el caso positivo:

\[x=f^{-1} (y)=2+\sqrt{y+3}\nonumber\]

Si el cuadrático no se hubiera dado en forma de vértice, reescribirlo en forma de vértice es probablemente el mejor enfoque. Alternativamente, podríamos haber tomado la ecuación estándar y reescribiéndola igual a cero:

\[0=x^{2} -4x+1-y\nonumber\]

Entonces podríamos usar la fórmula cuadrática con$a=1$,, y$b=-4$$c=(1-y)$, dando como resultado las mismas soluciones que encontramos anteriormente:

\[x=\dfrac{-(-4)\pm \sqrt{(-4)^{2} -4(1)(1-y)} }{2} =2\pm \dfrac{\sqrt{12+4y} }{2} =2\pm \sqrt{3+y}\nonumber \]

Ejercicio$\PageIndex{1}$

Encuentra la inversa de la función$f(x)=x^{2} +1$, en el dominio$x \ge 0$.

Responder: \[y=x^{2} +1\nonumber\]
\[y-1=x^{2}\nonumber\]
\[x=f^{-1} (y)=\sqrt{y-1}\nonumber\]

Si bien no es posible encontrar una inversa de la mayoría de las funciones polinómicas, algunos otros polinomios básicos son invertibles.

Ejemplo$\PageIndex{3}$

Encuentra la inversa de la función$f(x)=5x^{3} +1$.

Solución

Esta es una transformación de la función básica del kit de herramientas cúbicas, y en base a nuestro conocimiento de esa función, sabemos que es uno a uno. Resolviendo para lo inverso resolviendo para$x$

\[\begin{array}{l} {y=5x^{3} +1} \\ {y-1=5x^{3} } \\ {\dfrac{y-1}{5} =x^{3} } \\ {x=f^{-1} (y)=\sqrt[{3}]{\dfrac{y-1}{5} } } \end{array}\nonumber \]

Observe que esta inversa es también una transformación de una función de potencia con una potencia fraccionaria,$x^{1/3}$.

Ejercicio$\PageIndex{2}$

¿Qué funciones del kit de herramientas tienen funciones inversas sin restringir su dominio?

Responder: identidad, cúbico, raíz cuadrada, raíz cúbica

Además de ser importantes como función inversa, las funciones radicales son comunes en modelos físicos importantes.

Ejemplo$\PageIndex{4}$

La velocidad,$v$ en pies por segundo, de un automóvil que pisó los frenos se puede determinar en función de la longitud de las marcas de derrape que las llantas dejaron en el suelo. Esta relación viene dada por

\[v(d)=\sqrt{2gfd} \nonumber\]

En esta fórmula,$g$ representa la aceleración por gravedad (32 pies/seg${}^{2}$), d es la longitud de las marcas de derrape en pies, y$f$ es una constante que representa la fricción de la superficie. Un automóvil perdió el control sobre asfalto mojado, con un coeficiente de fricción de 0.5, dejando marcas de derrape de 200 pies. ¿Qué tan rápido viajaba el auto cuando perdió el control?

Solución

Usando los valores dados de$f$ = 0.5 y$d$ = 200, podemos evaluar la fórmula dada:

$v(200)=\sqrt{2(32)(0.5)(200)} =80$pies/seg, que es aproximadamente 54.5 millas por hora.

Cuando las funciones radicales se componen con otras funciones, determinar el dominio puede volverse más complicado.

Ejemplo$\PageIndex{5}$

Encuentra el dominio de la función$f(x)=\sqrt{\dfrac{(x+2)(x-3)}{(x-1)} }$.

Solución

Dado que una raíz cuadrada solo se define cuando la cantidad bajo el radical no es negativa, necesitamos determinar dónde$\dfrac{(x+2)(x-3)}{(x-1)} \ge 0$. Una función racional puede cambiar los signos (cambiar de positivo a negativo o viceversa) en las intercepciones horizontales y en las asíntotas verticales. Para esta ecuación, la gráfica podría cambiar los signos a$x$ = -2, 1 y 3.

Para determinar en qué intervalos la expresión racional es positiva, podríamos evaluar la expresión a los valores de prueba, o esbozar una gráfica. Si bien ambos enfoques funcionan igual de bien, para este ejemplo usaremos una gráfica.

Esta función tiene dos intercepciones horizontales, ambas de las cuales exhiben un comportamiento lineal, donde la gráfica pasará a través de la intercepción. Hay una asíntota vertical, que corresponde a un factor lineal, lo que lleva a un comportamiento similar a la función básica del kit de herramientas recíprocas. Hay una intercepción vertical en (0, 6). Esta gráfica no tiene una asíntota horizontal, ya que el grado del numerador es mayor que el grado del denominador.

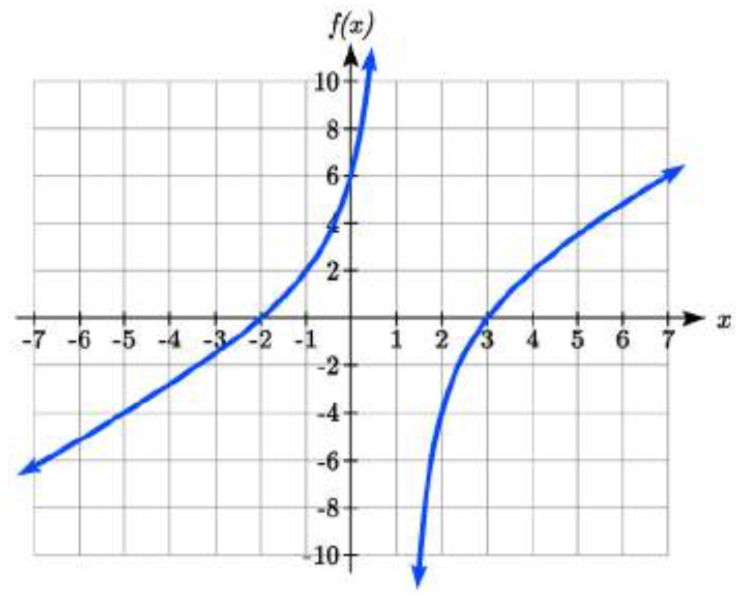$Una gráfica que comienza negativa y creciente, cruza el eje x en x=negativo 2, y aumenta hacia el infinito a medida que x se acerca a 1. A la derecha de 1 la gráfica aumenta desde el infinito negativo, cruza el eje x en x=3 y continúa aumentando.$ Desde la intercepción vertical y la intercepción horizontal en$x$ = -2, podemos bosquejar el lado izquierdo de la gráfica. A partir del comportamiento en la asíntota, podemos bosquejar el lado derecho de la gráfica.

A partir de la gráfica, ahora podemos decir en qué intervalos esta expresión será no negativa, por lo que se$f(x)$ definirá la función original.

$f(x)$tiene dominio$-2\le x<1\; or\; x\ge 3$, o en notación de intervalo,$[-2,1)\bigcup [3,\infty )$.

Al igual que con el hallazgo de inversos de funciones cuadráticas, a veces es deseable encontrar lo inverso de una función racional, particularmente de funciones racionales que son la relación de funciones lineales, como nuestros ejemplos de concentración.

Ejemplo$\PageIndex{6}$

La función$C(n)=\dfrac{20+0.4n}{100+n}$ se utilizó en la sección anterior para representar la concentración de una solución ácida después de que se hayan agregado$n$ mL de solución al 40% a 100 mL de una solución al 20%. Es posible que queramos poder determinar en su lugar la cantidad de solución al 40% que se ha agregado en función de la concentración actual de la mezcla.

Solución

Para ello, nos gustaría la inversa de esta función:

\[C=\dfrac{20+0.4n}{100+n}\nonumber\]multiplicar ambos lados por el denominador
\[C(100+n)=20+0.4n\nonumber\] distribuir
\[100C+Cn=20+0.4n\nonumber\] agrupar todo con$n$ en un lado
\[100C-20=0.4n-Cn\nonumber\] factor hacia fuera$n$
\[100C-20=(0.4-C)n\nonumber\] dividir para encontrar la inversa
\[n(C)=\dfrac{100C-20}{0.4-C}\nonumber\]

Si, por ejemplo, quisiéramos saber cuántos mL de solución al 40% deben agregarse para obtener una concentración del 35%, simplemente podemos evaluar la inversa en lugar de resolver una ecuación que involucre la función original:

$n(0.35)=\dfrac{100(0.35)-20}{0.4-0.35} =\dfrac{15}{0.05} =300$Se necesitaría agregar ml de solución al 40%.

Ejercicio$\PageIndex{3}$

Encuentra la inversa de la función$f(x)=\dfrac{x+3}{x-2}$.

Responder: \[y=\dfrac{x+3}{x-2}\nonumber\]
\[y(x-2)=x+3\nonumber\]
\[yx-2y=x+3\nonumber\]
\[yx-x=2y+3\nonumber\]
\[x(y-1)=2y+3\nonumber\]
\[f^{-1} (y)=\dfrac{2y+3}{y-1}\nonumber\]

Temas Importantes de esta Sección

Imponer un sistema de coordenadas
Encontrar una función inversa
Restringir el dominio
Funciones invertibles del kit de herramientas
Funciones radicales
Inversaciones de funciones racionales