4.3: Funciones logarítmicas

Se espera que una población de 50 moscas se duplique cada semana, lo que lleva a una función de la forma\(f(x)=50(2)^{x}\), donde x representa el número de semanas que han pasado. ¿Cuándo llegará esta población a 500? Tratar de resolver este problema lleva a:

\[500=50(2)^{x}\nonumber\]Dividiendo ambos lados por 50 para aislar el exponencial
\[10=2^{x}\nonumber\]

Si bien hemos configurado modelos exponenciales y los hemos usado para hacer predicciones, es posible que hayas notado que aún no se ha mencionado la resolución de ecuaciones exponenciales. La razón es simple: ninguna de las herramientas algebraicas discutidas hasta ahora es suficiente para resolver ecuaciones exponenciales. Considera la ecuación\(2^{x} =10\) anterior. Eso lo sabemos\(2^{3} =8\) y\(2^{4} =16\), por lo que es claro que\(x\) debe haber algún valor entre 3 y 4 ya que\(g(x)=2^{x}\) va en aumento. Podríamos usar la tecnología para crear una tabla de valores o gráfica para estimar mejor la solución.

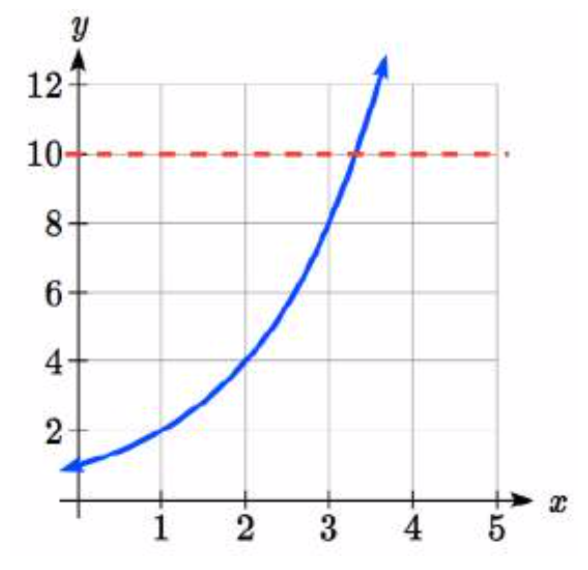
A partir de la gráfica, podríamos estimar mejor que la solución esté alrededor de 3.3. Este resultado sigue siendo bastante insatisfactorio, y dado que la función exponencial es uno a uno, sería genial tener una función inversa. Ninguna de las funciones que ya hemos discutido serviría como función inversa y así debemos introducir una nueva función, llamada log como la inversa de una función exponencial. Dado que las funciones exponenciales tienen diferentes bases, definiremos logaritmos correspondientes de diferentes bases también.

Definición: logaritmo

La función logaritmo (base\(b\)), escrita\(\log _{b} \left(x\right)\), es la inversa de la función exponencial (base\(b\)),\(b^{x}\).

Dado que el logaritmo y exponencial son inversos, se deduce que:

propiedades de registros: propiedades inversas

\[\log _{b} \left(b^{x} \right)=x\]

\[b^{\log _{b} x} =x\]

Recordemos de la definición de una función inversa que si\(f(a)=c\), entonces\(f^{-1} (c)=a\). Aplicando esto a las funciones exponencial y logarítmica, podemos convertir entre una ecuación logarítmica y su exponencial equivalente.

logaritmo equivalente a un exponencial

El enunciado\(b^{a} =c\) es equivalente al enunciado\(\log _{b} (c)=a\).

Alternativamente, podríamos mostrar esto comenzando con la función exponencial\(c=b^{a}\), luego tomando la base logarítmica\(b\) de ambos lados, dando\(\log _{b} (c)=\log _{b} b^{a}\). Usando la propiedad inversa de los registros, vemos eso\(\log _{b} (c)=a\).

Dado que log es una función, se escribe más correctamente como\(\log _{b} (c)\), usando paréntesis para denotar la evaluación de funciones, tal como lo haríamos con\(f(c)\). Sin embargo, cuando la entrada es una sola variable o número, es común ver los paréntesis caídos y la expresión escrita como\(\log _{b} c\).

Ejemplo\(\PageIndex{1}\)

Escribe estas ecuaciones exponenciales como ecuaciones logarítmicas:

1. \(2^{3} =8\)
2. \(5^{2} =25\)
3. \(10^{-4} =\dfrac{1}{10000}\)

Solución

a)\(2^{3} =8\) es equivalente a\(\log _{2} (8)=3\)

b)\(5^{2} =25\) es equivalente a\(\log _{5} (25)=2\)

c)\(10^{-4} =\dfrac{1}{10000}\) es equivalente a\(\log _{10} \left(\dfrac{1}{10000} \right)=-4\)

Ejemplo\(\PageIndex{2}\)

Escribe estas ecuaciones logarítmicas como ecuaciones exponenciales:

a)\(\log _{6} \left(\sqrt{6} \right)=\dfrac{1}{2}\) b)\(\log _{3} \left(9\right)=2\)

Solución

a)\(\log _{6} \left(\sqrt{6} \right)=\dfrac{1}{2}\) es equivalente a\(6^{1/2} =\sqrt{6}\)

b)\(\log _{3} \left(9\right)=2\) es equivalente a\(3^{2} =9\)

Ejercicio\(\PageIndex{1}\)

Escribe la ecuación exponencial\(4^{2} =16\) como una ecuación logarítmica.

Contestar

\[\log _{4} \left(16\right)=2=\log _{4} 4^{2} =2\log _{4} 4\nonumber\]

Al establecer la relación entre funciones exponenciales y logarítmicas, ahora podemos resolver ecuaciones logarítmicas y exponenciales básicas mediante la reescritura.

Ejemplo\(\PageIndex{3}\)

Resolver\(\log _{4} \left(x\right)=2\) para\(x\).

Solución

Al reescribir esta expresión como exponencial,\(4^{2} =x\), así\(x = 16\).

Ejemplo\(\PageIndex{4}\)

Resolver\(2^{x} =10\) para\(x\).

Solución

Al reescribir esta expresión como logaritmo, obtenemos\(x=\log _{2} (10)\).

Si bien esto sí define una solución, y una solución exacta en eso, puede resultarle algo insatisfactoria ya que es difícil comparar esta expresión con la estimación decimal que hicimos anteriormente. Además, dar una expresión exacta para una solución no siempre es útil, muchas veces realmente necesitamos una aproximación decimal a la solución. Por suerte, esta es una tarea en las que las calculadoras y las computadoras son bastante adeptas. Por desgracia para nosotros, la mayoría de las calculadoras y computadoras solo evaluarán logaritmos de dos bases. Felizmente, esto termina por no ser un problema, como veremos brevemente.

Definición: logaritmos comunes y naturales

El logaritmo común es el logaritmo con base 10, y normalmente se escribe\(\log (x)\).

El logaritmo natural es el logaritmo con base\(e\), y normalmente se escribe\(\ln (x)\).

Ejemplo\(\PageIndex{5}\)

Evaluar\(\log (1000)\) usando la definición del registro común.

Valores del logaritmo común

número	número como exponencial	log (número)
1000	\(10^3\)	3
100	\(10^2\)	2
10	\(10^1\)	1
1	\(10^0\)	0
0.1	\(10^{-1}\)	-1
0.01	\(10^{-2}\)	-2
0.001	\(10^{-3}\)	-3

Solución

Para evaluar\(\log (1000)\), podemos dejar\(x=\log (1000)\), luego reescribir en forma exponencial usando la base logarítmica común de 10:

\(10^{x} =1000.\)

A partir de esto, podríamos reconocer que 1000 es el cubo de 10, así\(x\) = 3.

También podemos usar la propiedad inversa de los registros para escribir\(\log _{10} \left(10^{3} \right)=3\).

Ejercicio\(\PageIndex{2}\)

Evaluar\(\log (1000000)\).

Contestar

\[\log \left(1000000\right)=\log \left(10^{6} \right)=6\nonumber\]

Ejemplo\(\PageIndex{6}\)

Evaluar\(\ln \left(\sqrt{e} \right)\).

Solución

Podemos reescribir\(\ln \left(\sqrt{e} \right)\) como\(\ln \left(e^{1/2} \right)\). Dado que ln es una base logarítmica\(e\), podemos usar la propiedad inversa para los registros:\[\ln \left(e^{1/2} \right)=\log _{e} \left(e^{1/2} \right)=\dfrac{1}{2}\nonumber\].

Ejemplo\(\PageIndex{7}\)

Evalúa el registro (500) usando tu calculadora o computadora.

Solución

Usando una computadora, podemos evaluar\(\log (500)\approx 2.69897\)

Para utilizar las funciones de logaritmo comunes o naturales para evaluar expresiones como\(\log _{2} (10)\), necesitamos establecer algunas propiedades adicionales.

propiedades de registros: propiedad exponente

\[\log _{b} \left(A^{r} \right)=r\log _{b} \left(A\right)\]

Para demostrar por qué esto es cierto, ofrecemos una prueba:

Dado que las funciones logarítmicas y exponenciales son inversas,\(b^{\log _{b} A} =A\).

Elevando ambos lados a la potencia r, obtenemos\(A^{r} =\left(b^{\log _{b} A} \right)^{r}\).

Utilizando la regla exponencial que establece\(\left(x^{p} \right)^{q} =x^{pq}\),\(A^{r} =\left(b^{\log _{b} A} \right)^{r} =b^{r\log _{b} A}\)

Tomando el tronco de ambos lados,\(\log _{b} \left(A^{r} \right)=\log _{b} \left(b^{r\log _{b} A} \right)\)

Al utilizar la propiedad inversa en el lado derecho se obtiene el resultado:\(\log _{b} \left(A^{r} \right)=r\log _{b} A\)

Ejemplo\(\PageIndex{8}\)

Reescribir\(\log _{3} \left(25\right)\) usando la propiedad exponente para registros.

Solución

Desde 25 = 5\({}^{2}\),

\[\log _{3} \left(25\right)=\log _{3} \left(5^{2} \right)=2\log _{3} \left(5\right)\nonumber\]

Ejemplo\(\PageIndex{9}\)

Reescribir\(4\ln (x)\) usando la propiedad exponente para registros.

Solución

Usando la propiedad a la inversa,\(4\ln (x)=\ln \left(x^{4} \right)\).

Ejercicio\(\PageIndex{3}\)

Reescribir usando la propiedad exponente para registros:\(\ln \left(\dfrac{1}{x^{2} } \right)\).

Contestar

\[3. \ln \left(\dfrac{1}{x^{2} } \right)=\ln \left(x^{-2} \right)=-2\ln (x)\nonumber \]

La propiedad exponente nos permite encontrar un método para cambiar la base de una expresión logarítmica.

propiedades de troncos: cambio de base

\[\log _{b} \left(A\right)=\dfrac{\log _{c} (A)}{\log _{c} (b)}\nonumber\]

Prueba

Vamos\(\log _{b} \left(A\right)=x\).

La reescritura como un exponencial da\(b^{x} =A\).

Tomando la base logarítmica c de ambos lados de esta ecuación da

\[\log _{c} b^{x} =\log _{c} A \nonumber\]

Ahora utilizando la propiedad de exponente para registros en el lado izquierdo,

\[x\log _{c} b=\log _{c} A \nonumber\]

Dividiendo, obtenemos\(x=\dfrac{\log _{c} A}{\log _{c} b}\). Reemplazar nuestra expresión original por\(x\),

\[\log _{b} A=\dfrac{\log _{c} A}{\log _{c} b} \nonumber\]

Con este cambio de fórmula base, finalmente podemos encontrar una buena aproximación decimal a nuestra pregunta desde el inicio de la sección.

Ejemplo\(\PageIndex{10}\)

Evaluar\(\log _{2} (10)\) usando el cambio de fórmula base.

Solución

De acuerdo con el cambio de fórmula base, podemos reescribir el log base 2 como un logaritmo de cualquier otra base. Dado que nuestras calculadoras pueden evaluar el logaritmo natural, podríamos elegir usar el logaritmo natural, que es la base logarítmica\(e\):

\[\log _{2} 10=\dfrac{\log _{e} 10}{\log _{e} 2} =\dfrac{\ln 10}{\ln 2}\nonumber\]

Usando nuestras calculadoras para evaluar esto,

\[\dfrac{\ln 10}{\ln 2} \approx \dfrac{2.30259}{0.69315} \approx 3.3219\nonumber\]

Esto finalmente nos permite responder a nuestra pregunta original: la población de moscas que discutimos al inicio de la sección tardará 3.32 semanas en crecer a 500.

Ejemplo\(\PageIndex{11}\)

Evaluar\(\log _{5} (100)\) usando el cambio de fórmula base.

Solución

Podemos reescribir esta expresión usando cualquier otra base. Si nuestras calculadoras son capaces de evaluar el logaritmo común, podríamos reescribir usando el log común, base 10.

\[\log _{5} (100)=\dfrac{\log _{10} 100}{\log _{10} 5} \approx \dfrac{2}{0.69897} =2.861 \nonumber\]

Si bien podemos resolver la ecuación exponencial básica\(2^{x} =10\) reescribiendo en forma logarítmica y luego usando el cambio de fórmula base para evaluar el logaritmo, la prueba del cambio de fórmula base ilumina un enfoque alternativo para resolver ecuaciones exponenciales.

Resolver ecuaciones exponenciales

1. Aísle las expresiones exponenciales cuando sea posible
2. Toma el logaritmo de ambos lados
3. Utilizar la propiedad de exponente para logaritmos para sacar la variable del exponente
4. Usa álgebra para resolver la variable.

Ejemplo\(\PageIndex{12}\)

Resolver\(2^{x} =10\) para\(x\).

Solución

Usando este enfoque alternativo, en lugar de reescribir este exponencial en forma logarítmica, tomaremos el logaritmo de ambos lados de la ecuación. Dado que a menudo deseamos evaluar el resultado a una respuesta decimal, generalmente utilizaremos el logaritmo común o el logaritmo natural. Para este ejemplo, usaremos el registro natural:

\[\ln \left(2^{x} \right)=\ln (10)\nonumber\]Utilizando la propiedad exponente para los registros,
\[x\ln \left(2\right)=\ln (10)\nonumber\] ahora dividiendo por ln (2),
\[x=\dfrac{\ln (10)}{\ln \left(2\right)} \approx 3.3219\nonumber\]

Observe que este resultado coincide con el resultado que encontramos usando la fórmula de cambio de base.

Ejemplo\(\PageIndex{13}\)

En la primera sección, predijimos la población (en miles de millones) de la India\(t\) años después de 2008 mediante el uso de la función\(f(t)=1.14(1+0.0134)^{t}\). Si la población sigue siguiendo esta tendencia, ¿cuándo llegará la población a los 2 mil millones?

Solución

Tenemos que resolver por tiempo para\(t\) que eso\(f(t) = 2\).

\[2=1.14(1.0134)^{t}\nonumber\]Dividir por 1.14 para aislar la expresión exponencial
\[\dfrac{2}{1.14} =1.0134^{t}\nonumber\] Toma el logaritmo de ambos lados de la ecuación
\[\ln \left(\dfrac{2}{1.14} \right)=\ln \left(1.0134^{t} \right)\nonumber\] Aplicar la propiedad de exponente en el lado derecho
\[\ln \left(\dfrac{2}{1.14} \right)=t\ln \left(1.0134\right)\nonumber\] Divide ambos lados por ln (1.0134)
\[t=\dfrac{\ln \left(\dfrac{2}{1.14} \right)}{\ln \left(1.0134\right)} \approx 42.23\text{ years}\nonumber\]

Si esta tasa de crecimiento continúa, el modelo predice que la población de la India alcanzará los 2 mil millones aproximadamente 42 años después de 2008, o aproximadamente en el año 2050.

Ejercicio\(\PageIndex{4}\)

Resolver\(5(0.93)^{x} =10\).

Contestar

\[5(0.93)^{x} =10(0.93)^{x} =2\ln \left(0.93^{x} \right)=\ln \left(2\right)x\ln \left(0.93\right)=\ln \left(2\right)\dfrac{\ln (2)}{\ln (0.93)} \approx -9.5513\nonumber\]

Ejemplo\(\PageIndex{14}\)

Resolver\(5(1.07)^{3t} =2\)

Solución

Para comenzar, queremos aislar la parte exponencial de la expresión, la\((1.07)^{3t}\), por lo que está sola en un lado de la ecuación. Entonces podemos usar el log para resolver la ecuación. Podemos usar cualquier log base; esta vez usaremos el log común.

\[5(1.07)^{3t} =2\nonumber\]Divide ambos lados por 5 para aislar el exponencial
\[(1.07)^{3t} =\dfrac{2}{5}\nonumber\] Toma el tronco de ambos lados.
\[\log \left((1.07)^{3t} \right)=\log \left(\dfrac{2}{5} \right)\nonumber\]Usar la propiedad de exponente para registros
\[3t\log \left(1.07\right)=\log \left(\dfrac{2}{5} \right)\nonumber\] Dividir por\(3\log \left(1.07\right)\) en ambos lados
\[\dfrac{3t\log \left(1.07\right)}{3\log \left(1.07\right)} =\dfrac{\log \left(\dfrac{2}{5} \right)}{3\log \left(1.07\right)}\nonumber\] Simplificar y evaluar
\[t=\dfrac{\log \left(\dfrac{2}{5} \right)}{3\log \left(1.07\right)} \approx -4.5143\nonumber\]

Tenga en cuenta que al ingresar esa expresión en su calculadora, asegúrese de poner paréntesis alrededor de todo el denominador para asegurar el orden correcto de las operaciones:

log (2/5)/(3*log (1.07))

Además de resolver ecuaciones exponenciales, las expresiones logarítmicas son comunes en muchas situaciones físicas.

Ejemplo\(\PageIndex{15}\)

En química, el pH es una medida de la acidez o basicidad de un líquido. El pH está relacionado con la concentración de iones hidrógeno, [H\({}^{+}\)], medida en moles por litro, por la ecuación

\[pH=-\log \left(\left[H^{+} \right]\right)\]

Si un líquido tiene una concentración de 0.0001 moles por liber, determine el pH.

Determinar la concentración de iones hidrógeno de un líquido con pH de 7.

Solución

Para responder a la primera pregunta, evaluamos la expresión\(-\log \left(0.0001\right)\). Si bien podríamos usar nuestras calculadoras para esto, realmente no las necesitamos aquí, ya que podemos usar la propiedad inversa de los registros:

\[-\log \left(0.0001\right)=-\log \left(10^{-4} \right)=-(-4)=4\nonumber\]

Para responder a la segunda pregunta, necesitamos resolver la ecuación\(7=-\log \left(\left[H^{+} \right]\right)\). Comience aislando el logaritmo en un lado de la ecuación multiplicando ambos lados por -1:

\[-7=\log \left(\left[H^{+} \right]\right)\nonumber\]. Reescribir en forma exponencial da la respuesta:

\[\left[H^{+} \right]=10^{-7} =0.0000001\text{ moles per liter}\nonumber \]

Los logaritmos también nos proporcionan un mecanismo para encontrar modelos de crecimiento continuo para el crecimiento exponencial dados dos puntos de datos.

Ejemplo\(\PageIndex{16}\)

Una población crece de 100 a 130 en 2 semanas. Encuentra la tasa de crecimiento continuo.

Solución

Midiendo\(t\) en semanas, estamos buscando una ecuación para\(P(t)=ae^{rt}\) que\(P(0)\) = 100 y\(P(2)\) = 130. Usando el primer par de valores,

\(100=ae^{r\cdot 0}\), entonces\(a\) = 100.

Usando el segundo par de valores,

\[130=100e^{r\cdot 2}\nonumber\]Dividir por 100
\[\dfrac{130}{100} =e^{r2}\nonumber\] Toma el registro natural de ambos lados
\[\ln (1.3)=\ln \left(e^{r2} \right)\nonumber\] Usar la propiedad inversa de los troncos

\[\begin{array}{l} {\ln (1.3)=2r} \\ {r=\dfrac{\ln (1.3)}{2} \approx 0.1312} \end{array}\nonumber\]

Esta población está creciendo a una tasa continua de 13.12% semanales.

En general, podemos relacionar la forma estándar de un exponencial con la forma de crecimiento continuo señalando (usando k para representar la tasa de crecimiento continuo para evitar la confusión de usar r de dos maneras diferentes en la misma fórmula):

\[a(1+r)^{x} =ae^{kx}\]\[(1+r)^{x} =e^{kx}\]\[1+r=e^{k}\]

convertir entre tasa de crecimiento periódico a continuo

En la ecuación\(f(x)=a(1+r)^{x}\),\(r\) se encuentra la tasa de crecimiento periódico, el porcentaje de crecimiento cada periodo de tiempo (crecimiento semanal, crecimiento anual, etc.).

En la ecuación\(f(x)=ae^{kx}\),\(k\) se encuentra la tasa de crecimiento continuo.

Puede convertir entre estos usando:\(1+r=e^{k}\).

Recuerde que la tasa de crecimiento continuo\(k\) representa la tasa de crecimiento nominal antes de contabilizar los efectos de la composición continua, mientras que\(r\) representa el incremento porcentual real en una unidad de tiempo (una semana, un año, etc.).

Ejemplo\(\PageIndex{17}\)

Las ventas de una empresa pueden ser modelizadas por la función\(S(t)=5000e^{0.12t}\), con\(t\) medidas en años. Encuentra la tasa de crecimiento anual.

Solución

Señalando que\(1+r=e^{k}\), entonces\(r=e^{0.12} -1=0.1275\), por lo que la tasa de crecimiento anual es de 12.75%. La función de ventas también podría escribirse en el formulario\(S(t)=5000(1+0.1275)^{t}\).

Temas Importantes de esta Sección

• La función logarítmica como la inversa de la función exponencial
• Escribir expresiones logarítmicas y exponenciales
• Propiedades de troncos
• Propiedades inversas
• Propiedades exponenciales
• Cambio de base
• Tronco común
• Tronco natural
• Resolver ecuaciones exponenciales
• Conversión entre tasa de crecimiento periódico y continuo.