5.2: Ángulos

Debido a que muchas aplicaciones que involucran círculos también implican una rotación del círculo, es natural introducir una medida para la rotación, o ángulo, entre dos rayos (segmentos de línea) que emanan del centro de un círculo. La medida del ángulo con la que probablemente estés familiarizado son los grados, así que comenzaremos ahí.

Definición: medida de un ángulo

La medida de un ángulo es una medida entre dos líneas de intersección, segmentos de línea o rayos, comenzando en el lado inicial y terminando en el lado terminal. Es una medida rotacional, no una medida lineal.

Ángulos de medición

Definición: grados

Un grado es una medida del ángulo. Una rotación completa alrededor del círculo es igual a 360 grados, por lo que un grado es 1/360 de un círculo.

Un ángulo medido en grados siempre debe incluir la unidad “grados” después del número, o incluir el símbolo de grado\(^{\circ}\). Por ejemplo, 90 grados =\(90^{\circ}\).

Definición: posición estándar

Al medir ángulos en un círculo, a menos que se indique lo contrario, medimos ángulos en posición estándar: comenzando en el eje horizontal positivo y con rotación en sentido antihorario.

Ejemplo\(\PageIndex{1}\)

Dar la medida de grado del ángulo que se muestra en el círculo.

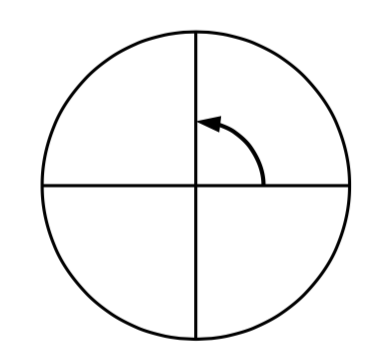
Solución

Las líneas verticales y horizontales dividen el círculo en cuartos. Dado que una rotación completa es de 360 grados=\(360{}^\circ\), cada cuarto de rotación es de 360/4 =\(90^{\circ}\) o 90 grados.

Ejemplo\(\PageIndex{2}\)

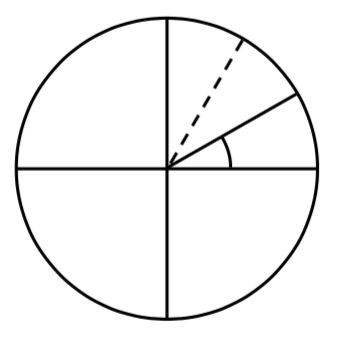
Mostrar un ángulo de\(30^{\circ}\) en el círculo.

Solución

Un ángulo de\(30^{\circ}\) es 1/3 de\(90^{\circ}\), así que dividiendo un cuarto de rotación en tercios, podemos esbozar una línea en\(30^{\circ}\).

Going Greek

Al representar ángulos usando variables, es tradicional usar letras griegas. Aquí hay una lista de letras griegas comúnmente encontradas.

\(\theta\)	\(varphi\)o\(\phi\)	\(\alpha\)	\(\beta\)	\(\gamma\)
theta	phi	alfa	beta	gamma

Trabajar con ángulos en grados

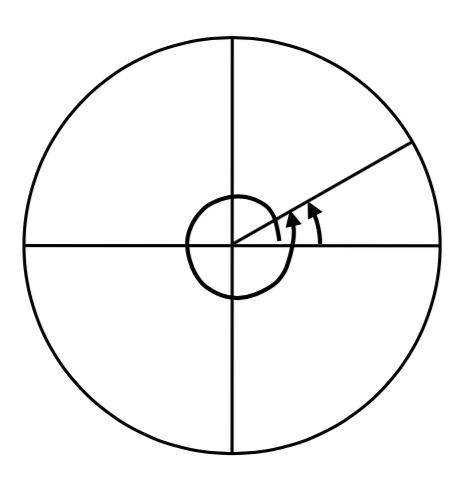Observe que dado que hay 360 grados en una rotación, un ángulo mayor a 360 grados indicaría más de 1 rotación completa. Mostrada en un círculo, la dirección resultante en la que apunta el lado terminal de este ángulo sería la misma que para otro ángulo entre 0 y 360 grados. Estos ángulos se llamarían coterminales.

ángulos coterminales

Después de completar su rotación completa en base al ángulo dado, dos ángulos son coterminales si terminan en la misma posición, por lo que sus lados terminales coinciden (apuntan en la misma dirección).

Ejemplo\(\PageIndex{3}\)

Encuentra un ángulo\(\theta\) que sea coterminal con\(800^{\circ}\), donde\(0^{\circ} \le \theta <360^{\circ}\)

Solución

Dado que sumar o restar una rotación completa, 360 grados, resultaría en un ángulo con el lado terminal apuntando en la misma dirección, podemos encontrar ángulos coterminales sumando o restando 360 grados. Un ángulo de 800 grados es coterminal con un ángulo de 800 - 360 = 440 grados. También sería coterminal con un ángulo de 440 - 360 = 80 grados.

El ángulo\(\theta =80^{\circ}\) es coterminal con\(800^{\circ}\).

Al encontrar el ángulo coterminal entre 0 y 360 grados, puede ser más fácil ver en qué dirección apunta el lado terminal de un ángulo.

Ejercicio\(\PageIndex{1}\)

Encuentra un ángulo\(\alpha\) que sea coterminal con\(870^{\circ}\), dónde\(0^{\circ} \le \alpha <360^{\circ}\).

Responder

\[\alpha =870-360-360=150^{\circ}\nonumber\]

En una recta numérica se mide un número positivo a la derecha y un número negativo se mide en la dirección opuesta (a la izquierda). De manera similar se mide un ángulo positivo en sentido contrario a las agujas del reloj y un ángulo negativo se mide en sentido contrario (en sentido horario).

Ejemplo\(\PageIndex{4}\)

Mostrar el ángulo\(-45^{\circ}\) en el círculo y encontrar un ángulo positivo\(\alpha\) que sea coterminal y\(0^{\circ} \le \alpha <360^{\circ}\).

Solución

Dado que 45 grados es la mitad de 90 grados, podemos comenzar en el eje horizontal positivo y medir la mitad de un ángulo de 90 grados en el sentido de las agujas del reloj.

Como podemos encontrar ángulos coterminales sumando o restando una rotación completa de 360 grados, podemos encontrar un ángulo coterminal positivo aquí sumando 360 grados:

\[-45^{\circ} +360^{\circ} =315^{\circ}\nonumber\]

Ejercicio\(\PageIndex{2}\)

Encuentra un\(\beta\) coterminal angular con\(-300^{\circ}\) donde\(0^{\circ} \le \beta <360^{\circ}\).

Responder

\[\beta =-300+360=60^{\circ}\nonumber\]

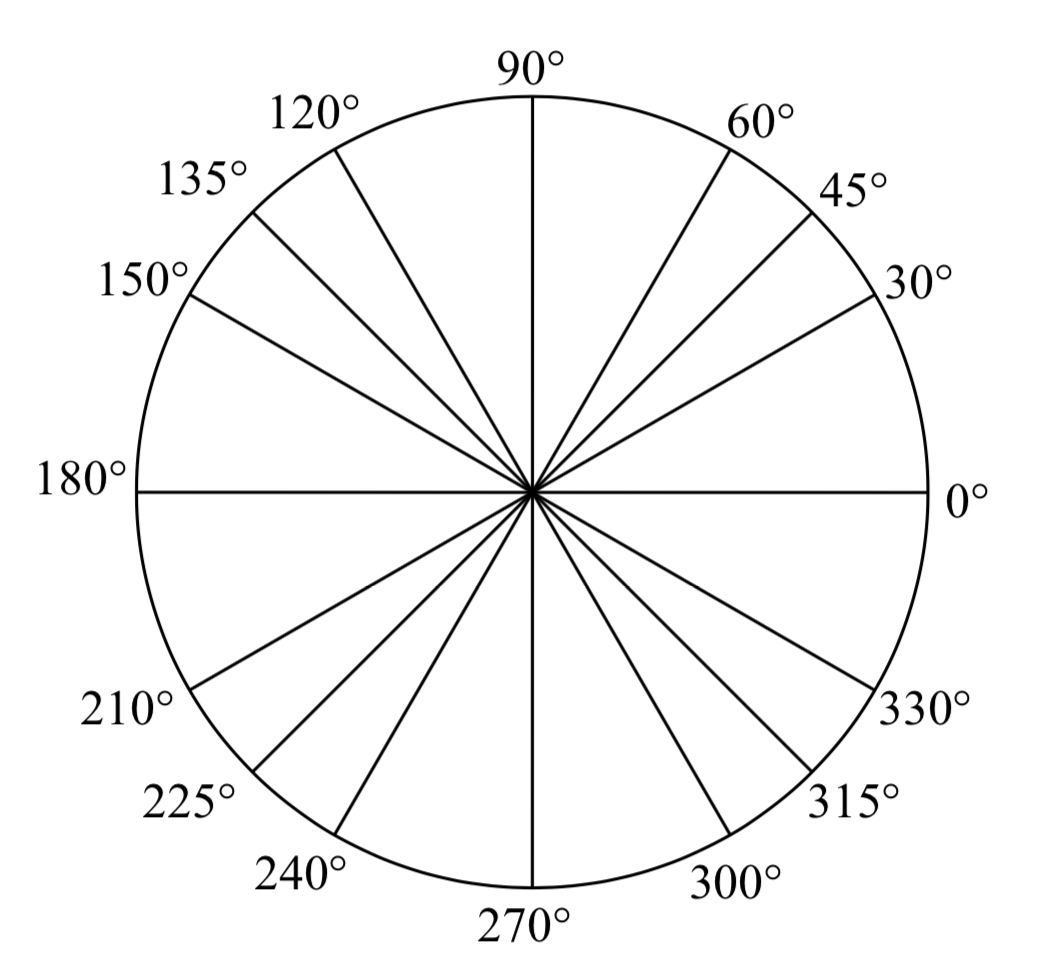Puede ser útil tener una familiaridad con los ángulos que se encuentran con frecuencia en una rotación de un círculo. Es común encontrar múltiplos de 30, 45, 60 y 90 grados. Estos valores se muestran a la derecha. Memorizar estos ángulos y comprender sus propiedades será muy útil ya que estudiamos las propiedades asociadas con los ángulos

Ángulos en Radianes

Si bien medir ángulos en grados puede ser familiar, hacerlo a menudo complica las cosas ya que las unidades de medida pueden interponerse en el camino de los cálculos. Por esta razón, se usa comúnmente otra medida de ángulos. Esta medida se basa en la distancia alrededor de un círculo.

Definición: arclongitud

Arclen gth es la longitud de un arco,\(s\), a lo largo de un círculo de radio\(r\) subtendido (dibujado) por un ángulo\(\theta\).

Es la porción de la circunferencia entre los lados inicial y terminal del ángulo.

La longitud del arco alrededor de un círculo completo se llama circunferencia de un círculo. La circunferencia de un círculo es\(C=2\pi r\). La relación entre la circunferencia y el radio, produce la constante\(2\pi\). Independientemente del radio, esta relación es siempre la misma, así como la medida de grado de un ángulo es independiente del radio.

Para elaborar esta idea, considera dos círculos, uno con radio 2 y otro con radio 3. Recordemos la circunferencia (perímetro) de un círculo es\(C=2\pi r\), donde\(r\) está el radio del círculo. El círculo más pequeño entonces tiene circunferencia\(2\pi (2)=4\pi\) y el más grande tiene circunferencia\(2\pi (3)=6\pi\).

Dibujando un ángulo de 45 grados en los dos círculos, podríamos estar interesados en la longitud del arco del círculo que indica el ángulo. En ambos casos, el ángulo de 45 grados dibuja un arco que es\({1/8}^{th}\) de la circunferencia completa, por lo que para el círculo más pequeño, la longitud del arco =\(\dfrac{1}{8} (4\pi )=\dfrac{1}{2} \pi\), y para el círculo más grande, la longitud del arco o longitud de arco =\(\dfrac{1}{8} (6\pi )=\dfrac{3}{4} \pi\).

Observe lo que sucede si encontramos la relación de la longitud del arco dividida por el radio del círculo:

Círculo más pequeño:\(\dfrac{\dfrac{1}{2} \pi }{2} =\dfrac{1}{4} \pi\)

Círculo más grande:\(\dfrac{\dfrac{3}{4} \pi }{3} =\dfrac{1}{4} \pi\)

La relación es la misma independientemente del radio del círculo — sólo depende del ángulo. Esta propiedad nos permite definir una medida del ángulo basada en la longitud del arco.

radianes

La medida radianes de un ángulo es la relación entre la longitud del arco circular subtendido por el ángulo y el radio del círculo.

En otras palabras, si s es la longitud de un arco de un círculo, y\(r\) es el radio del círculo, entonces

medida de radianes\(=\dfrac{s}{r}\)

Si el círculo tiene radio 1, entonces la medida del radián corresponde a la longitud del arco.

Debido a que la medida de radianes es la relación de dos longitudes, es una medida sin unidades. No es necesario escribir la etiqueta “radianes” después de una medida de radianes, y si ves un ángulo que no está etiquetado con “grados” o el símbolo de grado, debes asumir que es una medida de radianes.

Considerando el caso más básico, el círculo unitario (un círculo con radio 1), sabemos que 1 rotación equivale a 360 grados,\(360^{\circ}\). También podemos rastrear una rotación alrededor de un círculo encontrando la circunferencia,\(C=2\pi r\), y para el círculo unitario\(C=2\pi\). Estas dos formas diferentes de rotar alrededor de un círculo nos dan una manera de convertir de grados a radianes.

1 rotación =\(360{}^\circ\) =\(2\pi\) radianes

1/2 rotación =\(180{}^\circ\) =\(\pi\) radianes

1/4 de rotación =\(90{}^\circ\) =\(\dfrac{\pi }{2}\) radianes

Ejemplo\(\PageIndex{5}\)

Encuentra la medida de radianes de un tercio de una rotación completa.

Solución

Para cualquier círculo, la longitud del arco a lo largo de tal rotación sería un tercio de la circunferencia,\(C=\dfrac{1}{3} (2\pi r)=\dfrac{2\pi r}{3}\). La medida del radián sería la longitud del arco dividida por el radio:

\[\text{Radian measure} = \dfrac{2\pi r}{3r} =\dfrac{2\pi }{3}\]

convertir entre radianes y grados

1 grado =\(\dfrac{\pi }{180}\) radianes

o: para convertir de grados a radianes, multiplicar por\(\dfrac{\pi \text{radians}}{180^{\circ}}\)

1 radián =\(\dfrac{180}{\pi }\) grados

o: para convertir de radianes a grados, multiplicar por\(\dfrac{180^{\circ}}{\pi \text{radians}}\)

Conversión entre radianes y grados

Ejemplo\(\PageIndex{6}\)

Convertir\(\dfrac{\pi }{6}\) radianes a grados.

Solución

Ya que se nos da un problema en radianes y queremos grados, nos multiplicamos por\(\dfrac{180^{\circ}}{\pi }\).

Recuerda que los radianes son una medida sin unidades, así que no necesitamos escribir “radianes”.

\(\dfrac{\pi }{6}\)radianes =\(\dfrac{\pi }{6} \cdot \dfrac{180^{\circ}}{\pi } =30\) grados.

Ejemplo\(\PageIndex{7}\)

Convierte 15 grados a radianes.

Solución

En este ejemplo, comenzamos con grados y queremos radianes así que usamos la otra conversión\(\dfrac{\pi }{180^{\circ}}\) para que las unidades de grado cancelen y nos quede con la medida sin unidades de radianes.

15 grados =\(15^{\circ} \cdot \dfrac{\pi }{180^{\circ}} =\dfrac{\pi }{12}\)

Ejercicio\(\PageIndex{3}\)

Convertir\(\dfrac{7\pi }{10}\) radianes a grados.

Responder

\[\dfrac{7\pi }{10} \cdot \dfrac{180^{\circ} }{\pi } =126^{\circ}\nonumber\]

Así como enumeramos todos los ángulos comunes en grados en un círculo, también debemos enumerar los valores de radianes correspondientes para las medidas comunes de un círculo correspondientes a múltiplos de grados de 30, 45, 60 y 90 grados. Al igual que con las mediciones de grado, sería recomendable comprometerlas a la memoria.

Podemos trabajar con las medidas radianes de un ángulo de la misma manera que trabajamos con grados.

Ejemplo\(\PageIndex{8}\)

Encuentra un ángulo\(\beta\) que sea coterminal con\(\dfrac{19\pi }{4}\), dónde\(0\le \beta <2\pi\).

Solución

Al trabajar en grados, encontramos ángulos coterminales sumando o restando 360 grados, una rotación completa. De igual manera, en radianes, podemos encontrar ángulos coterminales sumando o restando rotaciones completas de\(2\pi\) radianes.

\[\dfrac{19\pi }{4} -2\pi =\dfrac{19\pi }{4} -\dfrac{8\pi }{4} =\dfrac{11\pi }{4}\nonumber\]

El ángulo\(\dfrac{11\pi }{4}\) es coterminal, pero no menor que\(2\pi\), por lo que restamos otra rotación.

\[\dfrac{11\pi }{4} -2\pi =\dfrac{11\pi }{4} -\dfrac{8\pi }{4} =\dfrac{3\pi }{4}\nonumber\]

El ángulo\(\dfrac{3\pi }{4}\) es coterminal con\(\dfrac{19\pi }{4}\).

Ejercicio\(\PageIndex{4}\)

Encuentra un ángulo\(\phi\) que sea coterminal con\(-\dfrac{17\pi }{6}\) donde\(0\le \phi <2\pi\).

Responder

\[-\dfrac{17\pi }{6} +2\pi +2\pi =-\dfrac{17\pi }{6} +\dfrac{12\pi }{6} +\dfrac{12\pi }{6} =\dfrac{7\pi }{6}\nonumber\]

Arclongitud y Área de un Sector

Recordemos que la medida radianes de un ángulo se definió como la relación de la longitud del arco de un arco circular al radio del círculo,\(\theta =\dfrac{s}{r}\). A partir de esta relación, podemos encontrar la longitud del arco a lo largo de un círculo dado un ángulo.

longitud de arco en un círculo

La longitud de un arco,\(s\), a lo largo de un círculo de radio\(r\) subtendido por ángulo\(\theta\) en radianes es

\[s=r\theta\]

Ejemplo\(\PageIndex{9}\)

Mercurio orbita el sol a una distancia aproximada de 36 millones de millas. En un día de la Tierra, completa 0.0114 rotación alrededor del sol. Si la órbita fuera perfectamente circular, ¿qué distancia a través del espacio recorrería Mercurio en un día terrestre?

Solución

Para comenzar, necesitaremos convertir el valor de rotación decimal a una medida de radianes.

Dado que una rotación =\(2\pi\) radianes,

0.0114 rotación =\(2\pi (0.0114)=0.0716\) radianes.

Combinando esto con el radio dado de 36 millones de millas, podemos encontrar la longitud del arco:

\(s=(36)(0.0716)=2.578\)millones de millas recorridas por el espacio.

Ejercicio\(\PageIndex{5}\)

Encuentra la longitud del arco a lo largo de un círculo de radio 10 subtendido por un ángulo de 215 grados.

Responder

215\(^{\circ}\) =\(\dfrac{215\pi }{180}\) radianes. \(s=10\cdot \dfrac{215\pi }{180} =\dfrac{215\pi }{18} \approx 37.525\)

Además de la longitud del arco, también podemos usar ángulos para encontrar el área de un sector de un círculo. Un sector es una porción de un círculo contenido entre dos líneas desde el centro, como una porción de pizza o pastel.

Recordemos que el área de un círculo con radio se\(r\) puede encontrar usando la fórmula\(A=\pi r^{2}\). Si un sector es cortado por un ángulo de\(\theta\), medido en radianes, entonces la fracción de círculo completo que ese ángulo ha recortado es\(\dfrac{\theta }{2\pi }\), ya que\(2\pi\) es una rotación completa. Así, el área del sector sería esta fracción de toda la zona:

\[\text{Area of sector}=\left(\dfrac{\theta }{2\pi } \right)\pi r^{2} =\dfrac{\theta \pi r^{2} }{2\pi } =\dfrac{1}{2} \theta r^{2}\nonumber\]

Definición: área de un sector

El área de un sector de un círculo w i-ésimo radio\(r\) subtendido por un ángulo\(\theta\), medido en radianes, es

\[\text{Area of sector}=\dfrac{1}{2} \theta r^{2}\]

Ejemplo\(\PageIndex{10}\)

Un aspersor automático para césped rocía una distancia de 20 pies mientras gira 30 grados. ¿Cuál es la zona del sector de pasto las aguas de aspersión?

Solución

Primero, necesitamos convertir la medida del ángulo en radianes. Dado que 30 grados es uno de nuestros ángulos comunes, lo ideal es que ya conozcas la medida equivalente en radianes, pero si no podemos convertir: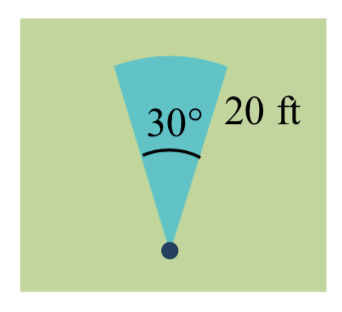

30 grados =\(30 \cdot \dfrac{\pi }{180} =\dfrac{\pi }{6}\) radianes.

El área del sector es entonces Área\(=\dfrac{1}{2} \left(\dfrac{\pi }{6} \right)(20)^{2} =104.72\) ft\({}^{2}\)

Ejercicio\(\PageIndex{6}\)

En el riego de pivote central, una gran tubería de riego sobre ruedas gira alrededor de un punto central, como se muestra aquí (http://commons.wikimedia.org/wiki/Fi... _otech_002.JPG CC-BY-SA). Un agricultor tiene un sistema de pivote central con un radio de 400 metros. Si las restricciones de agua solo le permiten regar 150 mil metros cuadrados diarios, ¿qué ángulo debería fijar para cubrir el sistema?

Responder

\(\dfrac{1}{2} \theta (400)^{2} =150,000\). \(\theta =1.875\), o\(107.43^{\circ}\)

Velocidad lineal y angular

Cuando tu auto conduce por una carretera, tiene sentido describir su velocidad en términos de millas por hora o metros por segundo. Estas son medidas de velocidad a lo largo de una línea, también llamada velocidad lineal. Cuando un punto en un círculo gira, describiremos su velocidad angular, o velocidad de rotación, en radianes por segundo, rotaciones por minuto o grados por hora.

Definición: velocidad angular y lineal

A medida que un punto se mueve a lo largo de un círculo de radio\(r\), su velocidad angular\(\omega\),, se puede encontrar como la rotación angular\(\theta\) por unidad de tiempo,\(t\).

\[\omega =\dfrac{\theta }{t}\]

La velocidad lineal,\(v\), del punto se puede encontrar como la distancia recorrida, longitud de arco\(s\), por unidad de tiempo,\(t\).

\[v=\dfrac{s}{t}\]

Ejemplo\(\PageIndex{11}\)

Una rueda hidráulica completa 1 rotación cada 5 segundos. Encuentra la velocidad angular en radianes por segundo. (http://en.Wikipedia.org/wiki/File:R%...m%C3%BChle.svg CC-BY)

Solución

La rueda completa 1 rotación =\(2\pi\) radianes en 5 segundos, por lo que la velocidad angular sería\(\omega =\dfrac{2\pi }{5} \approx 1.257\) radianes por segundo.

Combinando las definiciones anteriores con la ecuación arclength\(s=r\theta\),, podemos encontrar una relación entre velocidades angulares y lineales. La ecuación de velocidad angular se puede resolver para\(\theta\), dando\(\theta =\omega t\). Sustituir esto en la ecuación de longitud de arco da\(s=r\theta =r\omega t\).

Sustituyendo esto en la ecuación de velocidad lineal da

\(v=\dfrac{s}{t} =\dfrac{r\omega t}{t} =r\omega\)

relación entre velocidad lineal y angular

Cuando la velocidad angular se mide en radianes por unidad de tiempo, la velocidad lineal y la velocidad angular están relacionadas por la ecuación

\[v=r\omega\]

Ejemplo\(\PageIndex{12}\)

Una bicicleta tiene ruedas de 28 pulgadas de diámetro. Un tacómetro determina que las ruedas están girando a 180 RPM (revoluciones por minuto). Encuentra la velocidad que recorre la bicicleta por la carretera.

Solución

Aquí tenemos una velocidad angular y necesitamos encontrar la velocidad lineal correspondiente, ya que la velocidad lineal del exterior de las llantas es la velocidad a la que la bicicleta viaja por la carretera.

Comenzamos por convertir de rotaciones por minuto a radianes por minuto. Puede ser útil utilizar las unidades para realizar esta conversión

\[180\dfrac{\text{rotations}}{\text{minute}} \cdot \dfrac{2\pi \text{radians}}{\text{rotation}} =360\pi \dfrac{\text{radians}}{\text{minute}}\nonumber\]

Usando la fórmula desde arriba junto con el radio de las ruedas, podemos encontrar la velocidad lineal

\[v=(14 \text{inches})\left(360\pi \dfrac{\text{radians}}{\text{minute}} \right)=5040\pi \dfrac{\text{inches}}{\text{minute}}\nonumber\]

Quizás se esté preguntando a dónde fueron los “radianes” en esta última ecuación. Recuerda que los radianes son una medida sin unidades, por lo que no es necesario incluirlos.

Finalmente, es posible que deseemos convertir esta velocidad lineal en una medición más familiar, como millas por hora.

\[5040\pi \dfrac{\text{inches}}{\text{minute}} \cdot \dfrac{1 \text{feet}}{12 \text{inches}} \cdot \dfrac{1 \text{mile}}{5280 \text{feet}} \cdot \dfrac{60 \text{minutes}}{1 \text{hour}} =14.99\text{ miles per hour (mph)}\nonumber\]

Ejercicio\(\PageIndex{7}\)

Un satélite gira alrededor de la tierra a 27,934 kilómetros por minuto a una altitud de 242 km sobre la tierra. Si el radio de la tierra es de 6378 kilómetros, encuentra la velocidad angular del satélite.

Responder

\(v\)= 27934. \(r\)= 6378+242=6620. \(\omega =\dfrac{v}{r} =\dfrac{27934}{6620} =4.2196\)radianes por hora.

Temas Importantes de esta Sección

• Medida de grado de ángulo
• Medida radianes del ángulo
• Conversión entre grados y radianes
• Ángulos comunes en grados y radianes
• Ángulos coterminales
• Arclongitud
• Área de un sector
• Velocidad lineal y angular