5.3: Puntos en círculos usando seno y coseno

Última actualización
Guardar como PDF

Page ID: 116541

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Si bien es conveniente describir la ubicación de un punto en un círculo utilizando un ángulo o una distancia a lo largo del círculo, relacionar esta información con las coordenadas x e y y la ecuación circular que exploramos en la Sección 5.1 es una aplicación importante de la trigonometría.

Se envía una señal de socorro desde un velero durante una tormenta, pero la transmisión no está clara y el bote de rescate sentado en el puerto deportivo no puede determinar la ubicación del velero. Usando un radar de alta potencia, determinan que la señal de socorro proviene de una distancia de 20 millas en un ángulo de 225 grados del puerto deportivo. ¿Cuántas millas este/oeste y norte/sur del bote de rescate hay el velero varado?

En sentido general, para investigar esto, comenzamos por dibujar un círculo centrado en el origen con radio$r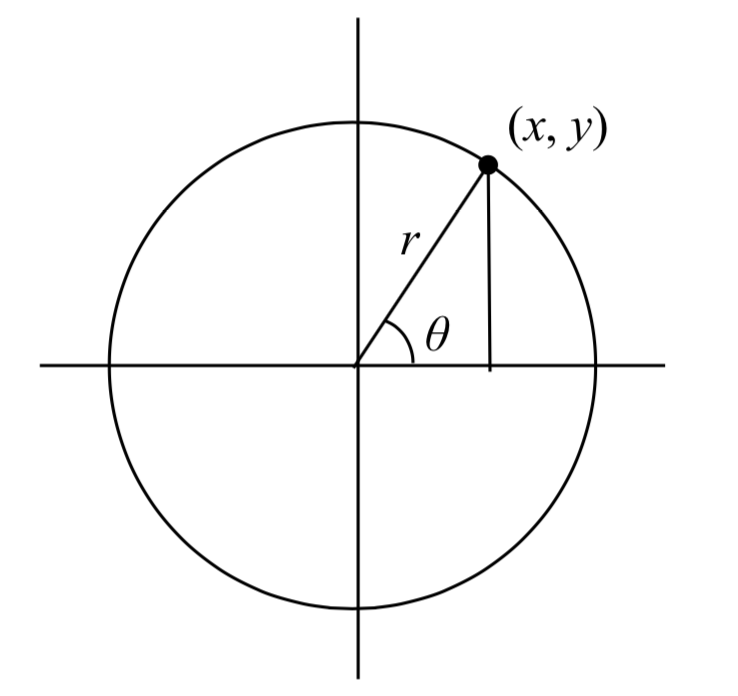$ $Un círculo centrado en el origen, con una línea etiquetada r dibujada en un ángulo theta, con el punto donde la línea se encuentra con el círculo etiquetado x coma y. Una vertical es la línea se dibuja desde el punto hacia abajo hasta el eje x.$ , y marcando el punto en el círculo indicado por algún ángulo$\theta$. Este punto tiene coordenadas ($x$,$y$).

Si dejamos caer un segmento de línea verticalmente hacia abajo desde este punto hasta el eje x, formaríamos un triángulo rectángulo dentro del círculo.

No importa en qué cuadrante nos$\theta$ coloque nuestro ángulo podemos dibujar un triángulo dejando caer un segmento de línea perpendicular al$x$ eje, teniendo en cuenta que los valores de$x$ y$y$ pueden ser positivos o negativos, dependiendo del cuadrante.

Adicionalmente, si el ángulo nos$\theta$ pone en un eje, simplemente medimos el radio como el$x$ o$y$ con el otro valor siendo 0, asegurando nuevamente que tenemos signos apropiados en las coordenadas con base en el cuadrante.

Los triángulos obtenidos de diferentes radios serán todos triángulos similares, es decir, los lados correspondientes escalan proporcionalmente. Si bien las longitudes de los lados pueden cambiar, como vimos en la última sección, las relaciones de las longitudes laterales siempre permanecerán constantes para cualquier ángulo dado.

$\dfrac{y_{1} }{r_{1} } =\dfrac{y_{2} }{r_{2} }$ $Un círculo centrado en el origen con una línea etiquetada r1 dibujada en un ángulo de theta. Desde el punto donde la línea se encuentra con el círculo se dibuja una línea vertical hacia abajo hasta el eje x, etiquetada como y1. La distancia horizontal desde el origen hasta esa línea vertical se etiqueta x1. Un segundo círculo se dibuja por separado con mayor radio con las mismas características, con lados etiquetados r2, y2 y x2.$

$\dfrac{x_{1} }{r_{1} } =\dfrac{x_{2} }{r_{2} }$

Para poder hacer referencia a estas proporciones más fácilmente, les daremos nombres. Dado que las relaciones dependen del ángulo, las escribiremos como funciones del ángulo$\theta$.

Nota: seno y coseno

$Un círculo centrado en el origen con una línea etiquetada r dibujada en un ángulo de theta. El punto donde la línea se encuentra con el círculo se etiqueta x coma y. Una línea vertical se dibuja desde ese punto hasta el eje x formando un triángulo, con la longitud vertical etiquetada y. La pata horizontal del triángulo desde el origen hasta la línea vertical se etiqueta x.$ Para el punto ($x$,$y$) en un círculo de radio$r$ en un ángulo de$\theta$, podemos definir dos funciones importantes como las relaciones de los lados del triángulo correspondiente:

La función sinusoidal:$\sin (\theta )=\dfrac{y}{r}$

La función coseno:$\cos (\theta )=\dfrac{x}{r}$

En este capítulo, exploraremos estas funciones utilizando tanto círculos como triángulos rectos. En el siguiente capítulo, analizaremos más de cerca el comportamiento y las características de las funciones sinusoidales y cosenales.

Ejemplo$\PageIndex{1}$

El punto (3, 4) está en el círculo de radio 5 en algún ángulo $\theta$. Encontrar$\cos (\theta )$ y$\sin (\theta )$.

Solución

Conociendo el radio del círculo y las coordenadas del punto, podemos evaluar las funciones coseno y seno como la relación de los lados.

\[\cos (\theta )=\dfrac{x}{r} =\dfrac{3}{5} \sin (\theta )=\dfrac{y}{r} =\dfrac{4}{5}\nonumber\]

Hay algunos valores coseno y seno que podemos determinar con bastante facilidad porque el punto correspondiente en el círculo cae sobre el$y$ eje$x$ o.

Ejemplo$\PageIndex{2}$

Encontrar$\cos (90{}^\circ )$ y$\sin (90{}^\circ )$.

$Un radio de círculo r centrado en el origen. Se dibuja una línea con longitud r a 90 grados hasta el punto 0 coma r.$

Solución

En cualquier círculo, el lado terminal de un ángulo de 90 grados apunta hacia arriba, por lo que las coordenadas del punto correspondiente en el círculo serían (0, r). Usando nuestras definiciones de coseno y seno,

\[\cos (90{}^\circ )=\dfrac{x}{r} =\dfrac{0}{r} =0\nonumber\]

\[\sin (90{}^\circ )=\dfrac{y}{r} =\dfrac{r}{r} =1\nonumber\]

Ejercicio$\PageIndex{1}$

Encuentra coseno y seno del ángulo$\pi$.

Contestar: \[\cos (\pi )=-1 \sin (\pi )=0\nonumber\]

Observe que las definiciones anteriores también pueden ser declaradas como:

coordenadas del punto en un círculo en un ángulo dado

En un círculo de radio$r$ en un ángulo de$\theta$, podemos encontrar las coordenadas del punto ($x$,$y$) Círculos:Puntos en un Círculo en ese ángulo usando

\[x=r\cos (\theta )\]

\[y=r\sin (\theta )\]

En un círculo unitario, un círculo con radio 1,$x=\cos (\theta )$ y$y=\sin (\theta )$.

Utilizando la ecuación básica para un círculo centrado en el origen$x^{2} +y^{2} =r^{2}$, combinado con las relaciones anteriores, podemos establecer una nueva identidad.

\[x^{2} +y^{2} =r^{2}\nonumber\]sustituir las relaciones anteriores,
\[(r\cos (\theta ))^{2} +(r\sin (\theta ))^{2} =r^{2}\nonumber\] simplificar,
\[r^{2} (\cos (\theta ))^{2} +r^{2} (\sin (\theta ))^{2} =r^{2}\nonumber\] dividir por$r^{2}$
\[(\cos (\theta ))^{2} +(\sin (\theta ))^{2} =1\nonumber\] o usar notación taquigráfica
\[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]

Aquí$\cos ^{2} (\theta )$ hay una notación taquigráfica de uso común para$(\cos (\theta ))^{2}$. Tenga en cuenta que muchas calculadoras y computadoras no entienden la notación taquigráfica.

En la Sección 5.1 relacionamos el Teorema$a^{2} +b^{2} =c^{2}$ de Pitágoras con la ecuación básica de un círculo$x^{2} +y^{2} =r^{2}$, que ahora hemos utilizado para llegar a la Identidad Pitagórica.

identidad pitagórica

La identidad pitagórica. Para cualquier ángulo $\theta$,\[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]

Un uso de esta identidad es que nos ayuda a encontrar un valor coseno de un ángulo si conocemos el valor sinusoidal de ese ángulo o viceversa. Sin embargo, dado que la ecuación producirá dos valores posibles, necesitaremos utilizar conocimientos adicionales del ángulo para ayudarnos a encontrar el valor deseado.

Ejemplo$\PageIndex{3}$

Si$\sin (\theta )=\dfrac{3}{7}$ y$\theta$ está en el segundo cuadrante, encuentra$\cos (\theta )$.

Solución

Sustituyendo el valor conocido por seno en la identidad pitagórica,

\[\cos ^{2} (\theta )+\sin ^{2} (\theta )=1\nonumber\]
\[\cos ^{2} (\theta )+\dfrac{9}{49} =1\nonumber\]
\[\cos ^{2} (\theta )=\dfrac{40}{49}\nonumber\]
\[\cos (\theta )=\pm \sqrt{\dfrac{40}{49} } =\pm \dfrac{\sqrt{40} }{7} =\pm \dfrac{2\sqrt{10} }{7}\nonumber\]

Dado que el ángulo está en el segundo cuadrante, sabemos que el$x$ valor del punto sería negativo, por lo que el valor del coseno también debería ser negativo. Usando esta información adicional, podemos concluir que\[\cos (\theta )=-\dfrac{2\sqrt{10} }{7}\nonumber\]

Valores para Seno y Coseno

En este punto, es posible que hayas notado que no hemos encontrado ningún valor de coseno o seno desde ángulos que no estén en un eje. Para ello, necesitaremos utilizar nuestro conocimiento de los triángulos.

Primero, considere un punto en un círculo en un ángulo de 45 de $Un círculo con radio 1 centrado en el origen. Se dibuja una línea a 45 grados y se dibuja un triángulo con la pata horizontal x y la pata vertical y. El punto donde la línea se encuentra con el círculo se etiqueta x coma y es igual a x coma x$ grees, o$\dfrac{\pi }{4}$. En este ángulo, las coordenadas x e y del punto correspondiente en el círculo serán iguales porque 45 grados dividen el primer cuadrante por la mitad. Dado que los$y$ valores$x$ y serán los mismos, los valores de seno y coseno también serán iguales. Utilizando la identidad pitagórica,

\[\cos ^{2} \left(\dfrac{\pi }{4} \right)+\sin ^{2} \left(\dfrac{\pi }{4} \right)=1\nonumber\]

ya que el seno y el coseno son iguales, podemos sustituir seno por coseno

\[\cos ^{2} \left(\dfrac{\pi }{4} \right)+\cos ^{2} \left(\dfrac{\pi }{4} \right)=1\nonumber\]agregar términos similares

\[2\cos ^{2} \left(\dfrac{\pi }{4} \right)=1\nonumber\]dividir

\[\cos ^{2} \left(\dfrac{\pi }{4} \right)=\dfrac{1}{2}\nonumber\]ya que el$x$ valor es positivo, vamos a mantener la raíz positiva

\[\cos \left(\dfrac{\pi }{4} \right)=\sqrt{\dfrac{1}{2} }\nonumber\]a menudo este valor se escribe con un denominador racionalizado

Recuerda, para racionalizar el denominador multiplicamos por un término equivalente a 1 para deshacernos del radical en el denominador.

\[\cos \left(\dfrac{\pi }{4} \right)=\sqrt{\dfrac{1}{2} } \sqrt{\dfrac{2}{2} } =\sqrt{\dfrac{2}{4} } =\dfrac{\sqrt{2} }{2}\nonumber\]

Ya que el seno y el coseno son iguales,$\sin \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}$ también. Las coordenadas ($x$,$y$) para un punto en un círculo de radio 1 en un ángulo de 45 grados son$\left(\dfrac{\sqrt{2} }{2} ,\dfrac{\sqrt{2} }{2} \right)$.

Ejemplo$\PageIndex{4}$

Encuentra las coordenadas del punto en un círculo de radio 6 en un ángulo de$\dfrac{\pi }{4}$.

Solución

Utilizando nuestro nuevo conocimiento que$\sin \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}$ y$\cos \left(\dfrac{\pi }{4} \right)=\dfrac{\sqrt{2} }{2}$, junto con nuestras relaciones que afirmaban$x=r\cos (\theta )$ y$y=r\sin (\theta )$, podemos encontrar las coordenadas del punto deseado:

\[x=6\cos \left(\dfrac{\pi }{4} \right)=6\left(\dfrac{\sqrt{2} }{2} \right)=3\sqrt{2}\nonumber \]\[y=6\sin \left(\dfrac{\pi }{4} \right)=6\left(\dfrac{\sqrt{2} }{2} \right)=3\sqrt{2}\nonumber\]

Ejercicio$\PageIndex{2}$

Encuentra las coordenadas del punto en un círculo de radio 3 en un ángulo de$90{}^\circ$.

Contestar: \[\begin{array}{l} {x=3\cos \left(\dfrac{\pi }{2} \right)=3\cdot 0=0} \\ {y=3\sin \left(\dfrac{\pi }{2} \right)=3\cdot 1=3} \end{array}\nonumber\]

A continuación, encontraremos el coseno y el seno en un ángulo de 30 grados, o$\frac{\pi }{6}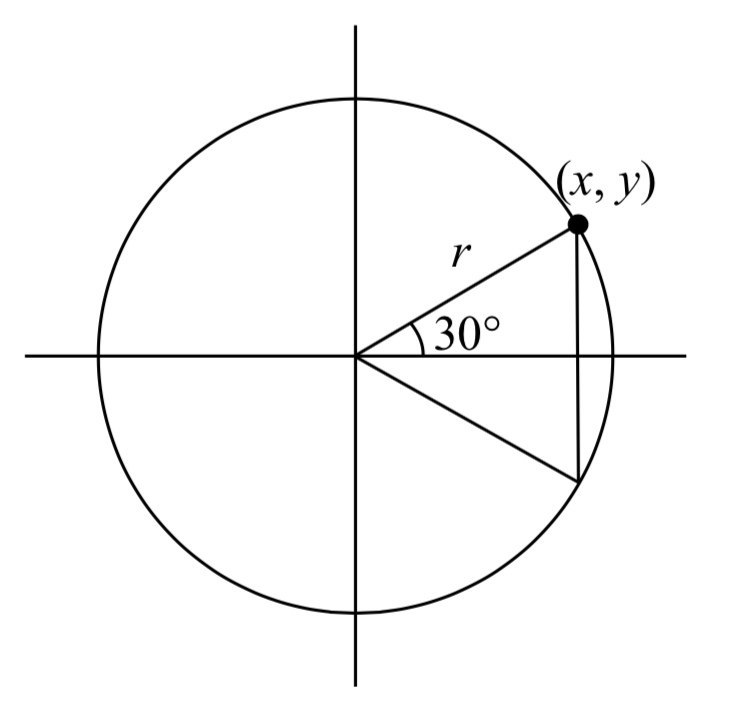$ $Un círculo con radio r con líneas dibujadas a 30 grados y negativos 30 grados. La línea a 30 grados se encuentra con el círculo en el punto x coma y, y una línea vertical se dibuja hacia abajo hasta el punto donde la otra línea se encuentra con el círculo, formando un triángulo.$ . Para ello, primero dibujaremos un triángulo dentro de un círculo con un lado en un ángulo de 30 grados, y otro en un ángulo de -30 grados. Si los dos triángulos rectos resultantes se combinan en un triángulo grande, observe que los tres ángulos de este triángulo más grande serán de 60 grados.

Como todos los ángulos son iguales, todos los lados también serán iguales. La línea $2019-07-05 9.33.35.png$ vertical tiene longitud$2y$, y como los lados son todos iguales podemos concluir que$2y = r$, o$y=\dfrac{r}{2}$. Usando esto, podemos encontrar el valor sinusoidal:

\[\text{sin}(\dfrac{\pi}{6}) = \dfrac{y}{r} = \dfrac{r/2}{r} = \dfrac{r}{2} \cdot \dfrac{1}{r} = \dfrac{1}{2}\nonumber\]

Usando la Identidad Pitagórica, podemos encontrar el valor del coseno:

\[\cos ^{2} \left(\dfrac{\pi }{6} \right)+\sin ^{2} \left(\dfrac{\pi }{6} \right)=1\nonumber\]
\[\cos ^{2} \left(\dfrac{\pi }{6} \right)+\left(\dfrac{1}{2} \right)^{2} =1\nonumber\]
\[\cos ^{2} \left(\dfrac{\pi }{6} \right)=\dfrac{3}{4}\nonumber\]ya que el$x$ valor es positivo, vamos a mantener la raíz positiva
\[\cos \left(\dfrac{\pi }{6} \right)=\sqrt{\dfrac{3}{4} } =\dfrac{\sqrt{3} }{2}\nonumber\]

Las coordenadas ($x$,$y$) para el punto en un círculo de radio 1 en un ángulo de 30 grados son$\left(\dfrac{\sqrt{3} }{2} ,\dfrac{1}{2} \right)$.

Dibujando un triángulo dentro del círculo unitario con un ángulo de 30 grados y reflejándolo sobre la línea$y = x$, podemos encontrar el coseno y el seno para 60 grados, o$\dfrac{\pi }{3}$, sin ningún trabajo adicional.

$Un radio de círculo 1 centrado en el origen. Una línea discontinua con la ecuación y es igual a x se dibuja a través del origen. Se dibuja una línea a 30 grados en sentido antihorario desde el eje x positivo, y una línea vertical se dibuja desde el extremo hacia abajo hasta el eje x formando un triángulo. La pata vertical tiene una longitud media, y la pata horizontal tiene una longitud de raíz cuadrada de 3 dividida por 2.$ $Un radio de círculo 1 centrado en el origen. Una línea discontinua con la ecuación y es igual a x se dibuja a través del origen. Se dibuja una línea a 30 grados en el sentido de las agujas del reloj desde el eje y positivo, también etiquetada 60 grados en sentido antihorario desde el eje x positivo, y una línea horizontal se dibuja desde el extremo izquierdo hasta el eje y formando un triángulo. La pata vertical tiene una longitud de raíz cuadrada de 3 dividida por 2, y la pata horizontal tiene una longitud media.$

Por esta simetría, podemos ver las coordenadas del punto en el círculo unitario en un ángulo de 60 grados será$\left(\dfrac{1}{2} ,\dfrac{\sqrt{3} }{2} \right)$, dando

$\cos \left(\dfrac{\pi }{3} \right)=\dfrac{1}{2}$y$\sin \left(\dfrac{\pi }{3} \right)=\dfrac{\sqrt{3} }{2}$

Ahora hemos encontrado los valores de coseno y seno para todos los ángulos comúnmente encontrados en el primer cuadrante del círculo unitario.

Ángulo	$0$	$\dfrac{\pi }{6}$, o 30$\mathrm{{}^\circ}$	$\dfrac{\pi }{4}$, o 45$\mathrm{{}^\circ}$	$\dfrac{\pi }{3}$, o 60$\mathrm{{}^\circ}$	$\dfrac{\pi }{2}$, o 90$\mathrm{{}^\circ}$
Coseno	1	$\dfrac{\sqrt{3} }{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{1}{2}$	0
Sine	0	$\dfrac{1}{2}$	$\dfrac{\sqrt{2} }{2}$	$\dfrac{\sqrt{3} }{2}$	1

Para cualquier ángulo dado en el primer cuadrante, habrá un ángulo en otro cuadrante con el mismo valor de seno, y otro ángulo más en otro cuadrante con el mismo valor de coseno. Dado que el valor de seno es la$y$ coordenada en el círculo unitario, el otro ángulo con el mismo seno compartirá el mismo$y$ valor, pero tendrá el$x$ valor opuesto. De igual manera, el ángulo con el mismo coseno compartirá el mismo$x$ valor, pero tendrá el$y$ valor opuesto.

Como se muestra aquí, el ángulo$\alpha$ tiene el mismo valor sinusoidal que el ángulo$\theta$; los valores coseno serían opuestos. El ángulo$\beta$ tiene el mismo valor coseno que el ángulo$\theta$; los valores sinusoidales serían opuestos.

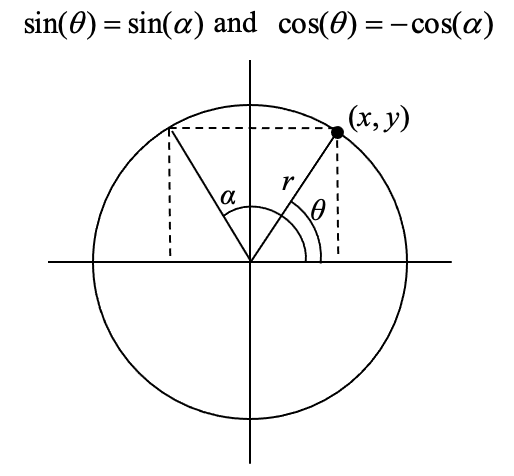
$Un círculo centrado con el origen, con una línea con longitud r en ángulo theta dibujada desde el centro hasta el punto x coma y en el círculo. Se dibuja una segunda línea en un ángulo alfa, que es una reflexión horizontal de la primera línea sobre el eje y. La segunda línea se encuentra con el círculo en un punto con el mismo valor y que la primera línea, y el valor x opuesto.$ $Un círculo centrado con el origen, con una línea con longitud r en ángulo theta dibujada desde el centro hasta el punto x coma y en el círculo. Se dibuja una segunda línea en un ángulo beta, que es una reflexión vertical de la primera línea sobre el eje x. La segunda línea se encuentra con el círculo en un punto con el mismo valor x que la primera línea, y el valor y opuesto.$

Es importante notar la relación entre los ángulos. Si, desde el ángulo, se midió el ángulo más pequeño con respecto al eje horizontal, todos tendrían la misma medida en valor absoluto. Decimos que todos estos ángulos tienen un ángulo de referencia de$\theta$.

Definición: ángulo de referencia

$Un círculo centrado en el origen, con una línea dibujada desde el origen en un ángulo de theta hasta un punto en el círculo etiquetado x coma y. Hay reflexión horizontal de esa línea en un ángulo theta en sentido horario desde el eje x negativo. Hay una reflexión vertical de la primera línea en un ángulo theta medido en sentido horario desde el eje x positivo. Hay una reflexión sobre ambos ejes en ángulo theta medido en sentido antihorario desde el eje x negativo. Todos los ángulos tienen medida theta desde el eje x hasta la línea. Las líneas discontinuas muestran las coordenadas x e y donde cada línea se encuentra con el círculo son iguales o opuestas.$ El ángulo de referencia de un ángulo es el tamaño del ángulo más pequeño con respecto al eje horizontal.

Un ángulo de referencia es siempre un ángulo entre 0 y 90 grados, o 0 y$\dfrac{\pi }{2}$ radianes.

Los ángulos comparten los mismos valores coseno y seno que sus ángulos de referencia, excepto los signos (positivos o negativos) que se pueden determinar a partir del cuadrante del ángulo.

Ejemplo$\PageIndex{5}$

Encuentra el ángulo de referencia de 150 grados. Úsalo para encontrar$\cos (150{}^\circ )$ y$\sin (150{}^\circ )$.

Solución

150 grados se ubica en el segundo cuadrante. Se encuentra a 30 grados de distancia del eje horizontal a 180 grados, por lo que el ángulo de referencia es de 30 grados.

Esto nos dice que 150 grados tiene los mismos valores de seno y coseno que 30 grados, a excepción de signo. Eso lo sabemos$\sin (30{}^\circ )=\dfrac{1}{2}$ y$\cos (30{}^\circ )=\dfrac{\sqrt{3} }{2}$. Dado que 150 grados está en el segundo cuadrante, la$x$ coordenada del punto en el círculo sería negativa, por lo que el valor del coseno será negativo. La$y$ coordenada es positiva, por lo que el valor sinusoidal será positivo.

\[\sin (150{}^\circ )=\dfrac{1}{2}\text{ and }\cos (150{}^\circ )=-\dfrac{\sqrt{3} }{2}\nonumber\]

Las coordenadas ($x$,$y$) para el punto en un círculo unitario en un ángulo de$150{}^\circ$ son$\left(\dfrac{-\sqrt{3} }{2} ,\dfrac{1}{2} \right)$.

Usando simetría y ángulos de referencia, podemos rellenar los valores de coseno y seno en el resto de los ángulos especiales en el círculo unitario. ¡Tómese el tiempo para aprender las coordenadas ($x$,$y$) de todos los ángulos principales en el primer cuadrante!

$Imagen de un círculo unitario con ángulos especiales y coordenadas de los puntos etiquetados. En el primer cuadrante, ángulo 0 en el punto 1 coma 0, ángulo 30 grados o pi sobre 6 en raíz cuadrada de 3 sobre 2 coma una mitad, ángulo 45 grados o pi sobre 4 en raíz cuadrada de 2 sobre 2 coma raíz cuadrada de 2 sobre 2, ángulo 60 grados o pi sobre 3 en una media coma raíz cuadrada de 3 sobre 2, ángulo 90 grados o pi sobre 2 a 0 coma 1. Los múltiplos de 30 grados y 45 grados en los otros cuadrantes se etiquetan con coordenadas reflejadas.$

Ejemplo$\PageIndex{6}$

Encuentra las coordenadas del punto en un círculo de radio 12 en un ángulo de$\dfrac{7\pi }{6}$.

Solución

Obsérvese que este ángulo está en el tercer cuadrante, donde tanto x como y son negativos. Tener esto en mente puede ayudarte a verificar tus signos de la función sinusoidal y coseno.

\[x=12\cos \left(\dfrac{7\pi }{6} \right)=12\left(\dfrac{-\sqrt{3} }{2} \right)=-6\sqrt{3}\nonumber \]\[y=12\sin \left(\dfrac{7\pi }{6} \right)=12\left(\dfrac{-1}{2} \right)=-6\nonumber\]

Las coordenadas del punto son$(-6\sqrt{3} ,-6)$.

Ejercicio$\PageIndex{3}$

Encuentra las coordenadas del punto en un círculo de radio 5 en un ángulo de$\dfrac{5\pi }{3}$.

Contestar: \[\left(5\cos \left(\dfrac{5\pi }{3} \right),5\sin \left(\dfrac{5\pi }{3} \right)\right)=\left(\dfrac{5}{2} ,\dfrac{-5\sqrt{3} }{2} \right)\nonumber\]

Ejemplo$\PageIndex{7}$

Ahora tenemos las herramientas para volver a la cuestión del velero planteada al inicio de esta sección.

Solución

Se envía una señal de socorro desde un velero durante una tormenta, pero la transmisión no está clara y el $Un círculo centrado en el origen, con una antena parabólica radar mostrada en el origen. Se muestra una línea en ángulo de 225 grados con una longitud de 20 millas, encontrándose con el círculo en un punto etiquetado con un velero.$ bote de rescate sentado en el puerto deportivo no puede determinar la ubicación del velero. Usando un radar de alta potencia, determinan que la señal de socorro proviene de un punto a 20 millas de distancia en un ángulo de 225 grados del puerto deportivo. ¿Cuántas millas este/oeste y norte/sur del bote de rescate hay el velero varado?

Ahora podemos responder a la pregunta encontrando las coordenadas del punto en un círculo con un radio de 20 millas en un ángulo de 225 grados.

\[x=20\cos \left(225{}^\circ \right)=20\left(\dfrac{-\sqrt{2} }{2} \right)\approx -14.142\text{ miles}\nonumber\]

\[y=20\sin \left(225{}^\circ \right)=20\left(\dfrac{-\sqrt{2} }{2} \right)\approx -14.142\text{ miles}\nonumber\]

El velero se encuentra a 14.142 millas al oeste y 14.142 millas al sur del puerto deportivo.

Los valores especiales de seno y coseno en el primer cuadrante son muy útiles de conocer, ya que conocerlos permite evaluar rápidamente el seno y el coseno de ángulos muy comunes sin necesidad de mirar una referencia o usar su calculadora. Sin embargo, sí surgen escenarios donde necesitamos conocer el seno y el coseno de otros ángulos.

Para encontrar el coseno y el seno de cualquier otro ángulo, recurrimos a una computadora o calculadora. Tenga en cuenta: la mayoría de las calculadoras se pueden establecer en modo “grado” o “radián”, que le dice a la calculadora las unidades para el valor de entrada. Cuando evalúas “cos (30)” en tu calculadora, la evaluará como el coseno de 30 grados si la calculadora está en modo grados, o el coseno de 30 radianes si la calculadora está en modo radianes. La mayoría de los programas informáticos con funciones coseno y seno solo funcionan en modo radián.

Ejemplo$\PageIndex{8}$

Evaluar el coseno de 20 grados usando una calculadora o computadora.

Solución

En una calculadora que se puede poner en modo grados, se puede evaluar esto directamente para que sea aproximadamente 0.939693.

En una computadora o calculadora sin modo de grado, primero necesitaría convertir el ángulo a radianes, o evaluar equivalentemente la expresión\[\cos \left(20 \cdot \dfrac{\pi }{180} \right)\nonumber\]

Temas Importantes de esta Sección

La función sinusoidal
La función coseno
Identidad pitagórica
Valores del círculo unitario
Ángulos de referencia
Uso de la tecnología para encontrar puntos en un círculo

Ángulo	\(0\)	\(\dfrac{\pi }{6}\), o 30\(\mathrm{{}^\circ}\)	\(\dfrac{\pi }{4}\), o 45\(\mathrm{{}^\circ}\)	\(\dfrac{\pi }{3}\), o 60\(\mathrm{{}^\circ}\)	\(\dfrac{\pi }{2}\), o 90\(\mathrm{{}^\circ}\)
Coseno	1	\(\dfrac{\sqrt{3} }{2}\)	\(\dfrac{\sqrt{2} }{2}\)	\(\dfrac{1}{2}\)	0
Sine	0	\(\dfrac{1}{2}\)	\(\dfrac{\sqrt{2} }{2}\)	\(\dfrac{\sqrt{3} }{2}\)	1

Search

Text Color

Text Size

Margin Size

Font Type