6.2: Gráficas de las Otras Funciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 116703

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, exploraremos las gráficas de las otras cuatro funciones trigonométricas. Comenzaremos con la función tangente. Recordemos que en el Capítulo 5 definimos tangente como$y$/$x$o seno/coseno, así se puede pensar en la tangente como la pendiente de una línea a través del origen haciendo el ángulo dado con el$x$ eje positivo.

En un ángulo de 0, la línea sería horizontal con una pendiente de cero. A medida que el ángulo aumenta hacia$\pi $ /2, el slo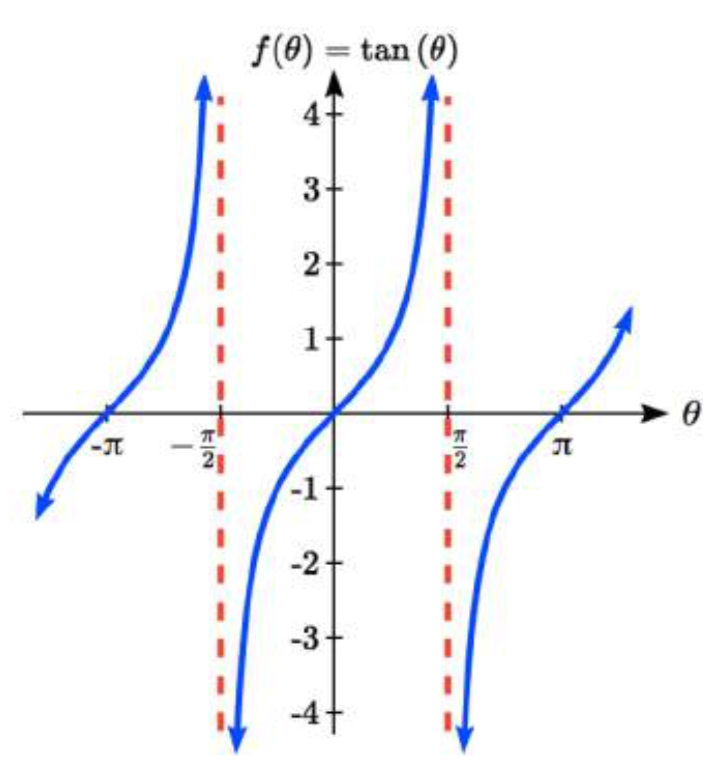 $Una gráfica de tangente de theta. Las líneas discontinuas que muestran asíntotas verticales se dibujan en theta es igual a pi negativo sobre 2 y a pi sobre 2. Entre estas asíntotas, la gráfica aumenta, cóncava hacia abajo a la izquierda del origen, y cóncava hasta la derecha del origen, acercándose al infinito a medida que theta se acerca a pi sobre 2 desde la izquierda, y acercándose al infinito negativo a medida que theta se acerca a pi negativo sobre 2 desde la derecha. Esta forma se repite a la izquierda y a la derecha, por lo que otro segmento a la derecha de pi sobre 2 pasa por pi coma 0.$ pe aumenta cada vez más. En un ángulo de$\pi $ /2, la línea sería vertical y la pendiente estaría indefinida. Inmediatamente pasado$\pi $ /2, la línea tendría una pendiente negativa pronunciada, dando un gran valor tangente negativo. Hay una ruptura en la función en$\pi $ /2, donde el valor de la tangente salta de positivo grande a negativo grande.

Podemos usar estas ideas junto con la definición de tangente para bosquejar una gráfica. Dado que tangente se define como seno/coseno, podemos determinar que tangente será cero cuando seno es cero: at -$\pi $, 0$\pi $, y así sucesivamente. De igual manera, la tangente será indefinida cuando el coseno sea cero: at -$\pi $ /2,$\pi $ /2, y así sucesivamente.

La tangente es positiva de 0 a$\pi $ /2 y$\pi $ a 3$\pi $ /2, correspondiente a los cuadrantes 1 y 3 del círculo unitario.

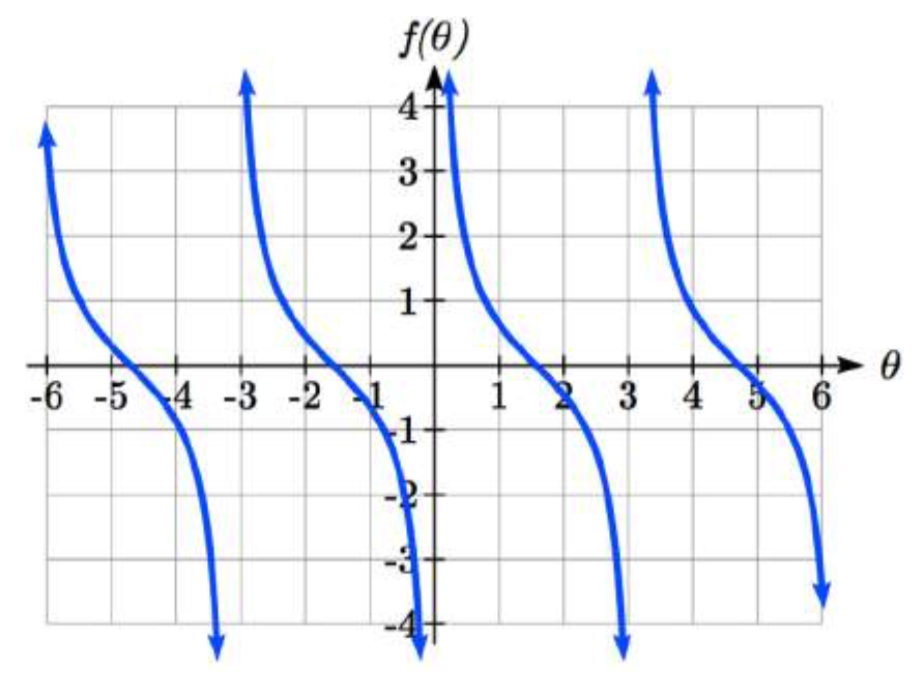
Usando la tecnología, podemos obtener una gráfica de tangente en una cuadrícula estándar.

$Una gráfica de tangente de theta sobre un eje estándar$

Observe que la gráfica parece repetirse. Para cualquier ángulo en el círculo, hay un segundo ángulo con la misma pendiente y valor tangente a la mitad del círculo, por lo que la gráfica se repite con un periodo de$\pi $; podemos ver un ciclo continuo de -$\pi $ /2 a$\pi $ /2, antes de que salte y se repita.

La gráfica tiene asíntotas verticales y la tangente no está definida dondequiera que una línea en ese ángulo sea vertical: en$\pi $ /2, 3$\pi $ /2, y así sucesivamente. Si bien el dominio de la función es limitado de esta manera, el rango de la función es todo números reales.

CARACTERÍSTICAS DEL GRÁFICO

El gráfico de la función tangente$m(\theta )=\tan (\theta )$

El periodo de la función tangente es$\pi $
El dominio de la función tangente es$\theta \ne \dfrac{\pi }{2} +k\pi$, donde$k$ es un entero
El rango de la función tangente es todos los números reales,$(-\infty ,\infty )$

Con la función tangente, al igual que las funciones seno y coseno, los estiramientos/compresiones horizontales son distintos de los estiramientos/compresiones verticales. El estiramiento horizontal normalmente se puede determinar a partir del periodo de la gráfica. Con las gráficas tangentes, a menudo es necesario determinar un estiramiento vertical usando un punto en la gráfica.

Ejemplo$\PageIndex{1}$

Encuentra una fórmula para la función graficada aquí.

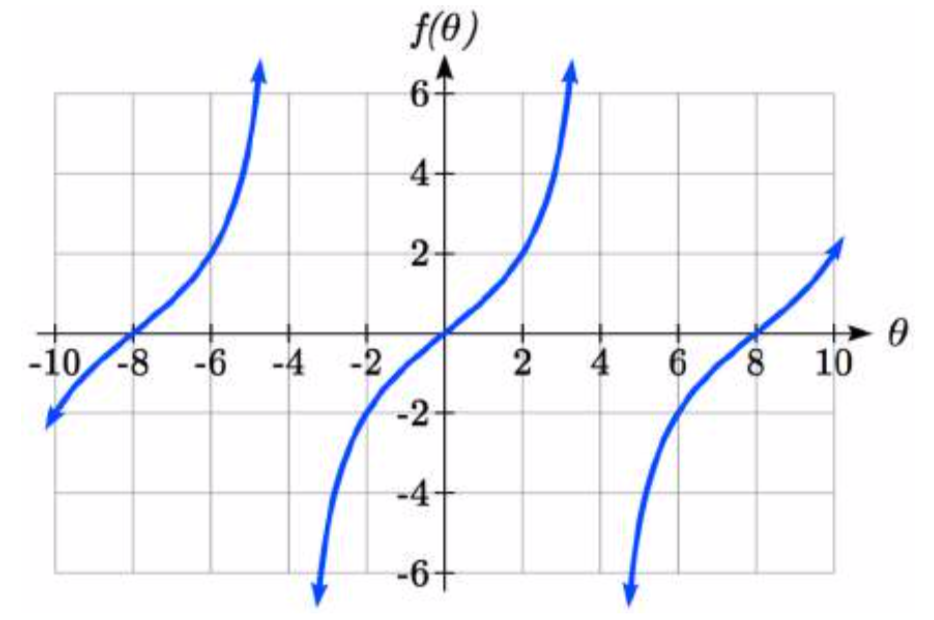
$Una gráfica que muestra tres segmentos crecientes, cada uno cóncavo hacia abajo al principio, luego cambiando a cóncavo hacia arriba. El primer segmento pasa por negativo 8 coma 0, el segundo por el origen, y el tercero a través de 8 coma 0. El segmento medio se acerca al infinito negativo a medida que theta se acerca al negativo 4 desde la derecha y se acerca al infinito a medida que theta se acerca a 4 desde la izquierda.$

Solución

La gráfica tiene la forma de una función tangente, sin embargo el periodo parece ser 8. Podemos ver un ciclo completo continuo de -4 a 4, sugiriendo un estiramiento horizontal. Para estirar$\pi $ a 8, los valores de entrada tendrían que ser multiplicados por$\dfrac{8}{\pi }$. Dado que la constante$k$ in$f(\theta )=a\tan \left(k\theta \right)$ es el recíproco del estiramiento horizontal$\dfrac{8}{\pi }$, la ecuación debe tener forma

\[f(\theta )=a\tan \left(\dfrac{\pi }{8} \theta \right).\nonumber\]

También podemos pensar en esto de la misma manera que lo hicimos con seno y coseno. El periodo de la función tangente es$\pi$ pero se ha transformado y ahora es 8; recuerda la relación del “periodo normal” al “nuevo periodo” es$\dfrac{\pi }{8}$ y así esto se convierte en el valor en el interior de la función que nos dice cómo se estiró horizontalmente.

Para encontrar el tramo vertical a, podemos usar un punto en la gráfica. Usando el punto (2, 2)

\[2=a\tan \left(\dfrac{\pi }{8} \cdot 2\right)=a\tan \left(\dfrac{\pi }{4} \right)\nonumber\]Desde\[\tan \left(\dfrac{\pi }{4} \right)=1,\quad a = 2\nonumber\]

Esta función tendría una fórmula\[f(\theta )=2\tan \left(\dfrac{\pi }{8} \theta \right)\nonumber\]

Ejercicio$\PageIndex{1}$

Dibuje una gráfica de$f(\theta )=3\tan \left(\dfrac{\pi }{6} \theta \right)$.

Responder: $Una gráfica tangente, con asimptos verticales en negativo 3 y 3. Hay segmentos crecientes entre y a cada lado de las asíntotas. El medio pasa por el origen, el siguiente pasa por 6 coma 0.$

Para la gráfica de secante, recordamos la identidad recíproca donde$\sec (\theta )=\dfrac{1}{\cos (\theta )}$. Observe que la función es indefinida cuando el coseno es 0, lo que lleva a una asíntota vertical en la gráfica en$\pi/2 $/$3\pi/2$,, etc. ya que el coseno siempre no es más de uno en valor absoluto, la secante, siendo la recíproca, siempre será no menor que uno en valor absoluto. Utilizando la tecnología, podemos generar la gráfica. La gráfica del coseno se muestra discontinua para que puedas ver la relación.

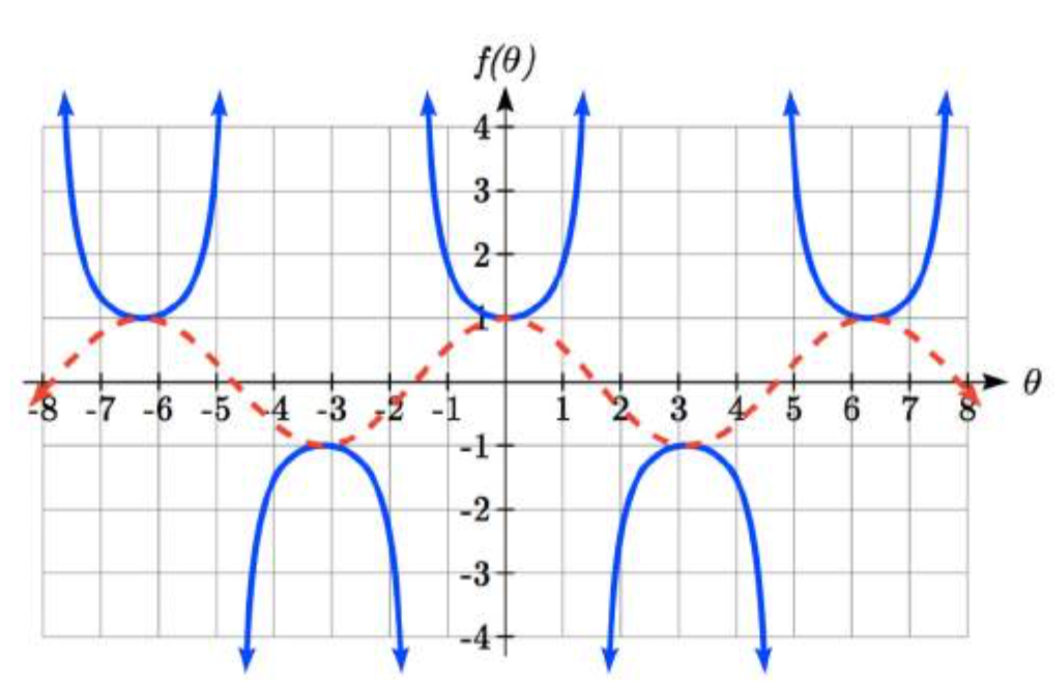
$Se muestra una gráfica de coseno discontinua. La gráfica de secante está formada por distintos segmentos en forma de U, cada uno entre asíntotas verticales ubicadas en cada valor donde el coseno es 0, incluyendo pi sobre 2 y 3 pi sobre 2. El segmento central en forma de U se abre hacia arriba, con el punto más bajo de la U tocando el pico del coseno a 0 coma 1. El siguiente segmento en forma de U se abre hacia abajo, con el punto más alto de la U invertida tocando el punto más bajo del coseno en pi coma negativo 1. Este patrón se repite, con cada segmento en forma de U tocando un pico de valle del coseno.$

\[f(\theta )=\sec (\theta )=\dfrac{1}{\cos (\theta )}\nonumber\]

La gráfica de cosecante es similar. De hecho, ya que$\sin (\theta )=\cos \left(\dfrac{\pi }{2} -\theta \right)$, se deduce que$\csc (\theta )=\sec \left(\dfrac{\pi }{2} -\theta \right)$, sugiriendo que la gráfica cosecante es un desplazamiento horizontal de la gráfica secante. Esta gráfica será indefinida donde sine es 0. Recordemos del círculo unitario que esto ocurre en 0$\pi $,, 2$\pi $, etc. La gráfica de seno se muestra discontinua junto con la gráfica del cosecante.

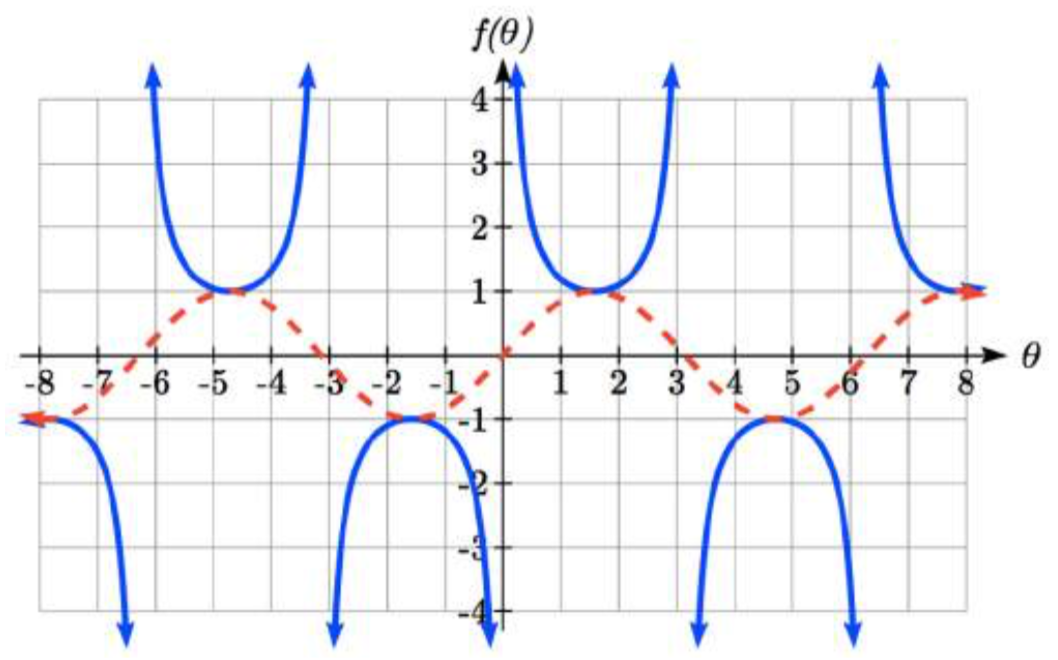
$Se muestra una gráfica de seno discontinua. La gráfica de cosecante está formada por distintos segmentos en forma de U, cada uno entre asíntotas verticales ubicadas en cada valor donde seno es 0, incluyendo 0 y pi. Un segmento en forma de U se abre hacia arriba, con el punto más bajo de la U tocando el pico del seno en pi sobre 2 coma 1. El siguiente segmento en forma de U se abre hacia abajo, con el punto más alto de la U invertida tocando el punto más bajo del seno a 3 pi sobre 2 comas negativas 1. Este patrón se repite, con cada segmento en forma de U tocando un pico de valle del seno.$

\[f(\theta )=\csc (\theta )=\dfrac{1}{\sin (\theta )}\nonumber\]

CARACTERÍSTICAS DE LA GRÁFICA DE SECANTE Y

Las gráficas secante y cosecante tienen período$2\pi $ como las funciones seno y coseno.

Secante tiene dominio$\theta \ne \dfrac{\pi }{2} +k\pi$, donde$k$ es un entero
Cosecante tiene dominio$\theta \ne k\pi$, donde$k$ es un entero
Tanto secante como cosecante tienen rango de$(-\infty ,-1]\bigcup [1,\infty )$

Ejemplo$\PageIndex{2}$

Dibuje una gráfica de$f(\theta )=2\csc \left(\dfrac{\pi }{2} \theta \right)+1$. ¿Cuál es el dominio y el rango de esta función?

Solución

La gráfica cosecante básica tiene asíntotas verticales en los múltiplos enteros de$\pi $. Debido al factor$\dfrac{\pi }{2}$ dentro del cosecante, la gráfica será comprimida por$\dfrac{2}{\pi }$, por lo que las asíntotas verticales se comprimirán a$\theta =\dfrac{2}{\pi } \cdot k\pi =2k$. En otras palabras, la gráfica tendrá asíntotas verticales en los múltiplos enteros de 2, y el dominio correspondientemente será$\theta \ne 2k$, donde$k$ es un entero.

El gráfico de seno básico tiene un rango de [-1, 1]. El estiramiento vertical en 2 estirará esto a [-2, 2], y el desplazamiento vertical hacia arriba 1 desplazará el rango de esta función a [-1, 3].

La gráfica cosecante básica tiene un rango de$(-\infty ,-1] \bigcup [1,\infty )$. El estiramiento vertical en 2 estirará esto a$(-\infty ,-2] \bigcup [2,\infty )$, y el desplazamiento vertical hacia arriba 1 desplazará el rango de esta función a$(-\infty ,-1] \bigcup [3,\infty )$.

El gráfico resultante se muestra a la derecha. 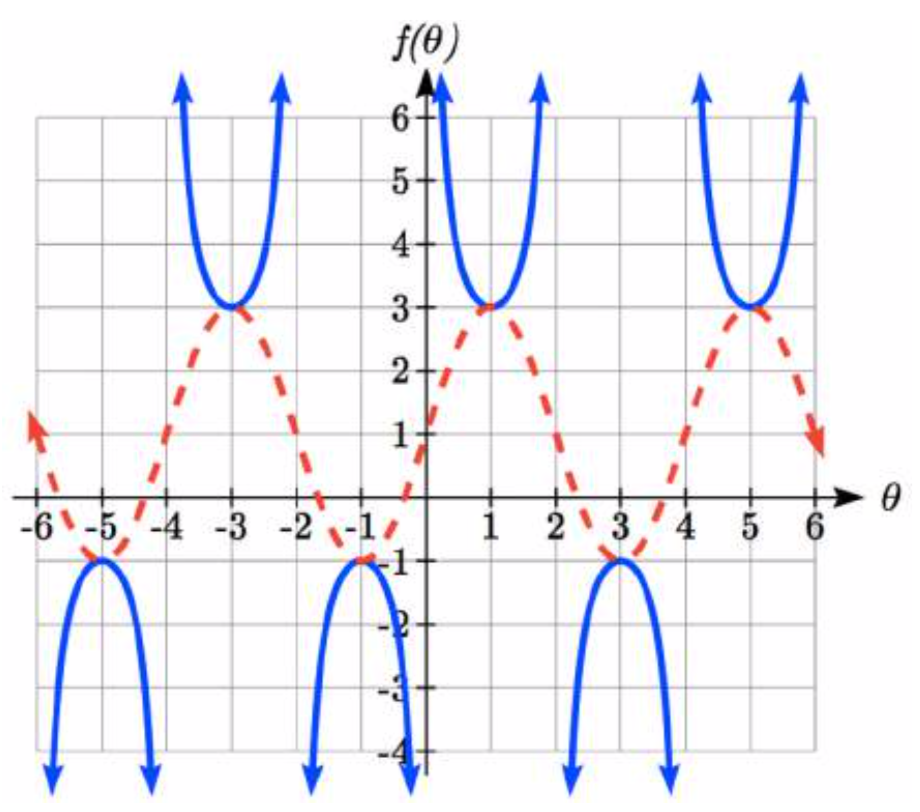$Una gráfica cosecante y sinusoidal mostrada en los mismos ejes. El gráfico sinusoidal es discontinuo, y tiene línea media en 1, amplitud 2, y un periodo de 4, alcanzando un pico en 1 coma 3 y un punto más bajo en 3 coma negativo 1, y tocando la línea media en 0 coma 1 y 2 coma 1. La gráfica cosecante tiene segmentos en forma de U. Un segmento se abre hacia arriba, tocando la gráfica sinusoidal en 1 coma 3, con asíntotas verticales a cada lado en 0 y 2. El siguiente segmento es de apertura hacia abajo, tocando la gráfica sinusoidal a 3 comas negativas 1, con asíntotas verticales a cada lado en 2 y 4.$

Observe cómo la gráfica del cosecante transformado se relaciona con la gráfica de trazos$f(\theta )=2\sin \left(\dfrac{\pi }{2} \theta \right)+1$ mostrados.

Ejercicio$\PageIndex{2}$

Dada la gráfica de que$f(\theta )=2\cos \left(\dfrac{\pi }{2} \theta \right)+1$ se muestra, bosquejar la gráfica de$g(\theta )=2\sec\left( \frac{\pi }{2}\theta \right)+1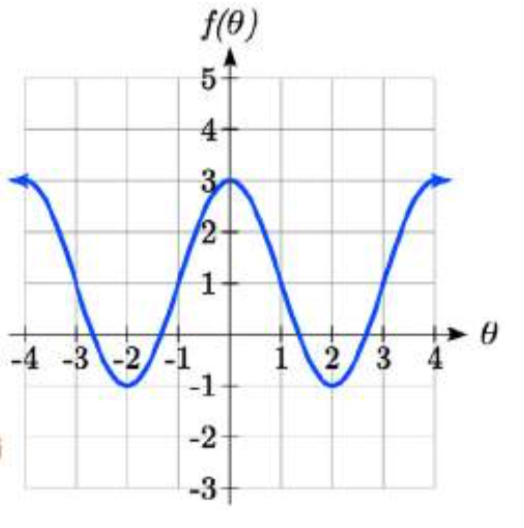$ $Una gráfica sinusoidal en forma de función coseno. Tiene un punto más bajo en negativo 2 coma negativo 2, un punto más alto en 0 coma 3, y otro punto más bajo en 2 coma negativo 1.$ en los mismos ejes.

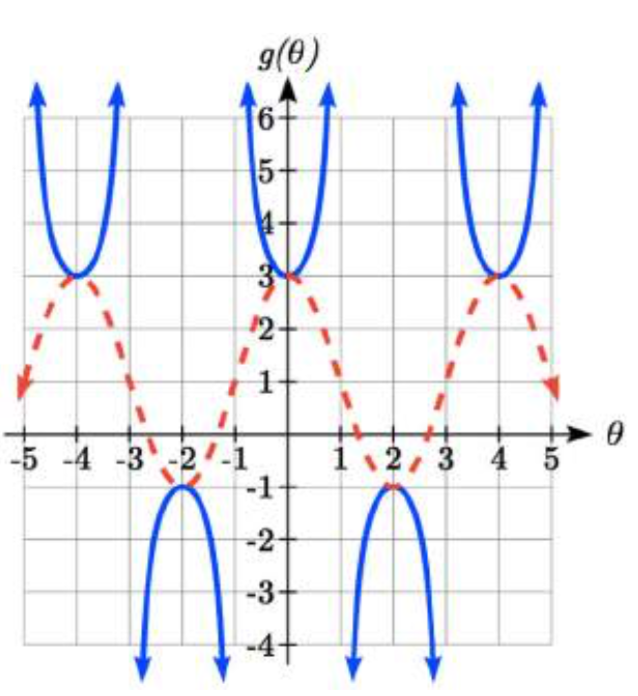
Responder: $Una gráfica secante, dibujada encima de una gráfica coseno. La gráfica secante tiene segmentos en forma de U de apertura hacia arriba con los puntos más bajos tocando la gráfica coseno a 0 coma 3 y 4 coma 3, y tiene segmentos en forma de U que se abren hacia abajo con los puntos más altos tocando la gráfica coseno en negativo 2 coma negativo 1 y 2 coma negativo 1.$

Por último, veremos la gráfica de cotangente. En base a su definición como la relación coseno a seno, quedará indefinido cuando el seno sea cero: a 0,$\pi $, 2$\pi $, etc. La gráfica resultante es similar a la de la tangente. De hecho, se trata de un flip horizontal y shift de la función tangente, como veremos en breve en el siguiente ejemplo.

$Una gráfica cotangente, similar a una gráfica tangente desplazada y invertida verticalmente. Tiene asíntotas verticales a 0, pi, 2 pi, etc, con segmentos decrecientes entre cada asíntota consecutiva. Un segmento se acerca al infinito a medida que theta se acerca a 0 desde la derecha, y disminuye cóncavo hasta pi sobre 2 coma 0, luego disminuye cóncava hacia abajo, acercándose al infinito a medida que theta se acerca a pi desde la izquierda.$

CARACTERÍSTICAS DE LA GRÁFICA DE

La gráfica cotangente tiene periodo$\pi $
Cotangente tiene dominio$\theta \ne k\pi$, donde$k$ es un entero
Cotangente tiene rango de todos los números reales,$(-\infty ,\infty )$

En la Sección 6.1, determinamos que la función sinusoidal era una función impar y el coseno era una función par al observar la gráfica y establecer las identidades de ángulo negativo para coseno y seno. Del mismo modo, puede notar en su gráfica que la función tangente parece ser impar. Podemos verificar esto usando las identidades de ángulo negativo para seno y coseno:

\[\tan \left(-\theta \right)=\dfrac{\sin \left(-\theta \right)}{\cos \left(-\theta \right)} =\dfrac{-\sin \left(\theta \right)}{\cos \left(\theta \right)} =-\tan \left(\theta \right)\nonumber\]

El secante, como el coseno en el que se basa, es una función par, mientras que el cosecante, como el seno, es una función impar.

IDENTIDADES DE ÁNGULO NEGATIVO TANGENTE, COTANGENTE, SECANTE

\[\tan \left(-\theta \right)=-\tan \left(\theta \right)\]

\[\cot \left(-\theta \right)=-\cot \left(\theta \right)\]

\[\sec \left(-\theta \right)=\sec \left(\theta \right)\]

\[\csc \left(-\theta \right)=-\csc \left(\theta \right)\]

Ejemplo$\PageIndex{3}$

$\tan \left(\theta \right)=-\cot \left(\theta -\dfrac{\pi }{2} \right)$Demuéstralo.

Solución

\[\tan \left(\theta \right)\nonumber\]Uso de la definición de tangente
\[=\dfrac{\sin \left(\theta \right)}{\cos \left(\theta \right)}\nonumber\] Uso de las identidades de cofunción
\[=\dfrac{\cos \left(\dfrac{\pi }{2} -\theta \right)}{\sin \left(\dfrac{\pi }{2} -\theta \right)}\nonumber\] Usar la definición de cotangente
\[=\cot \left(\dfrac{\pi }{2} -\theta \right)\nonumber\] Factorizar un negativo desde el interior
\[=\cot \left(-\left(\theta -\dfrac{\pi }{2} \right)\right)\nonumber\] Usar la identidad de ángulo negativo para cot
\[=-\cot \left(\theta -\dfrac{\pi }{2} \right)\nonumber\]

Temas Importantes de esta Sección

Las funciones tangente y cotangente
Periodo
Dominio
Rango
Las funciones secante y cosecante
Periodo
Dominio
Rango
Transformaciones
Identidades de ángulo negativo