6.5: Modelado con Funciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 116734

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Resolviendo triángulos rectos para ángulos

En la Sección 5.5, utilizamos trigonometría en un triángulo rectángulo para resolver los lados de un triángulo dado un lado y un ángulo adicional. Usando las funciones trigonométricas inversas, podemos resolver los ángulos de un triángulo rectángulo dados dos lados.

Ejemplo$\PageIndex{1}$

Un avión necesita volar a un aeródromo ubicado a 300 millas al este y 200 millas al norte de su ubicación actual. ¿A qué rumbo debería volar el avión? Es decir, si ignoramos la resistencia del aire o la velocidad del viento, ¿cuántos grados al norte del este debería volar el avión?

Solución

Podríamos comenzar por dibujar una imagen y etiquetar toda la información conocida.

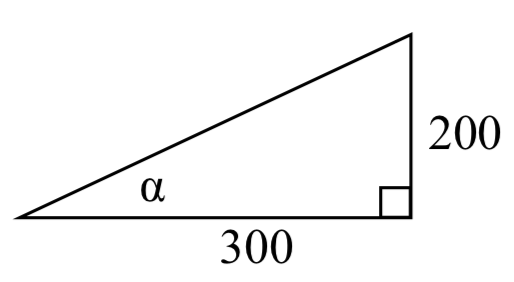
$Un triángulo rectángulo con longitud de patas 200 y 300. El ángulo entre la hipotenusa y la longitud de la pierna 300 está etiquetado como alfa.$

Dibujando un triángulo, vemos que estamos buscando el ángulo$\alpha$. En este triángulo, el lado opuesto al ángulo$\alpha$ es de 200 millas y el lado adyacente es de 300 millas. Como conocemos los valores para los lados opuestos y adyacentes, tiene sentido usar la función tangente.

\[\tan (\alpha )=\dfrac{200}{300} \nonumber\]

Usando la inversa,

\[\alpha =\tan ^{-1} \left(\dfrac{200}{300} \right)\approx 0.588 \nonumber\]

o equivalentemente alrededor de 33.7 grados.

El avión necesita volar a una dirección de 33.7 grados al norte del este.

Ejemplo$\PageIndex{2}$

Las regulaciones de seguridad de OSHA requieren que la base de una escalera se coloque a 1 pie de la pared por cada 4 pies de longitud de escalera (http://www.osha.gov/SLTC/etools/cons.../4ladders.html). Encuentra el ángulo que forma una escalera de este tipo con el suelo.

Solución

Para cualquier longitud de escalera, la base debe estar a una cuarta parte de la distancia que el pie de la escalera está lejos de la pared. Equivalentemente, si la base está a$a$ pies de la pared, la escalera puede tener$4a$ pies de largo. Dado que$a$ es el lado adyacente al ángulo y$4a$ es la hipotenusa, utilizamos la función coseno. a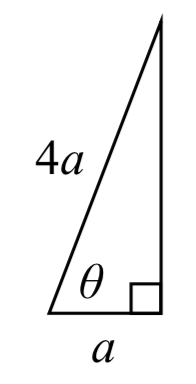 $Un triángulo rectángulo con longitud de pierna a y longitud de hipotenusa 4a y ángulo entre theta etiquetada.$

\[\cos (\theta )=\dfrac{a}{4a} =\dfrac{1}{4} \nonumber\]

Usando la inversa

\[\theta =\cos ^{-1} \left(\dfrac{1}{4} \right)\approx 75.52\, \text{degrees}\nonumber\]

La escalera forma un ángulo de 75.52 grados con el suelo.

Ejercicio$\PageIndex{1}$

Se debe reemplazar un cable que ancla el centro de la noria London Eye al suelo. El centro de la noria se encuentra a 70 metros sobre el suelo y el segundo anclaje en el suelo está a 23 metros de la base de la rueda. ¿Cuál es el ángulo desde el suelo hasta el centro de la noria y cuánto dura el cable?

Contestar: El ángulo de elevación para el cable es de 71.81 grados y el cable es de 73.68 m de largo

Ejemplo$\PageIndex{3}$

En un diseño de videojuego, un mapa muestra la ubicación de otros personajes en relación con el jugador, que se encuentra en el origen, y la dirección a la que están enfrentando. Actualmente un personaje se muestra en el mapa en las coordenadas (-3, 5). Si el jugador gira 20 grados en sentido antihorario, entonces los objetos en el mapa girarán correspondientemente 20 grados en el sentido de las agujas del reloj. Encuentra las nuevas coordenadas del personaje.

Solución

Para rotar la posición del personaje, podemos imaginarlo como un punto en un círculo, y cambiaremos el ángulo del punto 20 grados. Para ello, primero necesitamos encontrar el radio de este círculo y el ángulo original.

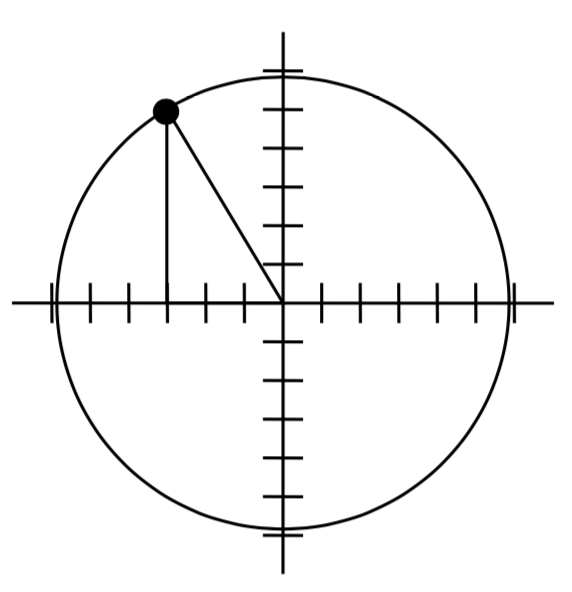
$Un círculo centrado en el origen. El punto negativo 3 coma 5 se muestra en el círculo. Se dibuja una línea desde el origen hasta el punto, y desde el punto verticalmente hacia abajo hasta el eje x.$

Dibujando un triángulo rectángulo dentro del círculo, podemos encontrar el radio usando el Teorema de Pitágoras:

\[\begin{array}{l} {\left(-3\right)^{2} +5^{2} =r^{2} } \\ {r=\sqrt{9+25} =\sqrt{34} } \end{array}\nonumber\]

Para encontrar el ángulo, tenemos que decidir primero si vamos a encontrar el ángulo agudo del triángulo, el ángulo de referencia, o si vamos a encontrar el ángulo medido en posición estándar. Si bien cualquiera de los dos enfoques funcionará, en este caso haremos lo último. Ya que para cualquier punto de un círculo sabemos$x=r\cos (\theta )$, usando nuestra información dada obtenemos

\[ \begin{align*} -3&=\sqrt{34} \cos (\theta ) \\[4pt] \dfrac{-3}{\sqrt{34} } &=\cos (\theta ) \\[4pt] \theta &=\cos ^{-1} \left(\dfrac{-3}{\sqrt{34} } \right)\approx 120.964{}^\circ \end{align*}\]

Si bien hay dos ángulos que tienen este valor coseno, el ángulo de 120.964 grados está en el segundo cuadrante como se desee, por lo que es el ángulo que buscábamos.

Girando el punto en el sentido de las agujas del reloj 20 grados, el ángulo del punto disminuirá a 100.964 grados. Luego podemos evaluar las coordenadas del punto girado

\[\begin{align*} x &= \sqrt{34} \text{cos} (100.964^{\circ}) \approx -1.109 \\[4pt] y &= \sqrt{34} \text{sin} (100.964^{\circ}) \approx 5.725 \end{align*}\]

Las coordenadas del personaje en el mapa rotado serán (-1.109, 5.725).

Modelado con funciones sinusoidales

Muchas situaciones de modelado involucran funciones que son periódicas. Anteriormente aprendimos que las funciones sinusoidales son un tipo especial de función periódica. Los problemas que involucran cantidades que oscilan a menudo pueden ser modelados por una función sinusoidal o coseno y una vez que creamos un modelo adecuado para el problema podemos usar ese modelo para responder diversas preguntas.

Ejemplo$\PageIndex{4}$

Las horas de luz diurna en Seattle oscilan de un mínimo de 8.5 horas en enero a un máximo de 16 horas en julio (www.mountaineers.org/seattle/... ylightHrs.html). ¿Cuándo debes plantar un jardín si quieres hacerlo durante un mes donde hay 14 horas de luz diurna?

Solución

Para modelar esto, primero observamos que las horas de luz diurna oscilan con un periodo de 12 meses. $B=\dfrac{2\pi }{12} =\dfrac{\pi }{6}$corresponde al tramo horizontal, encontrado utilizando la relación entre el periodo original y el nuevo periodo.

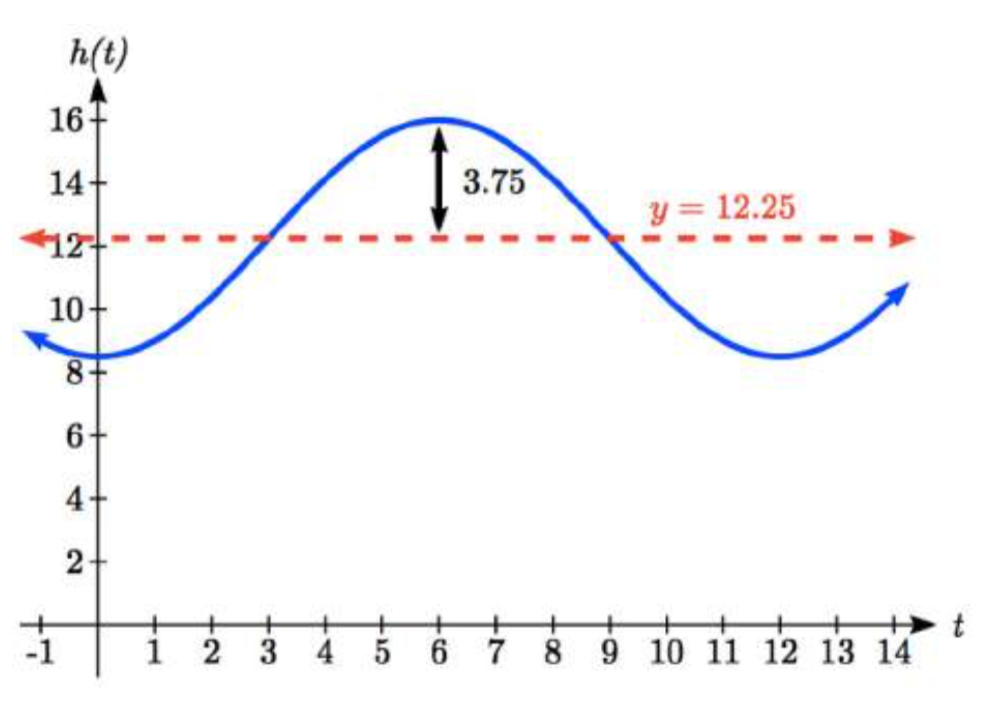
$Una función sinusoidal mostrada en una ventana de t igual a 0 a t es igual a 14. La gráfica comienza en el valor más bajo en 0 coma 8.5, luego aumenta hasta un máximo en 6 coma 16, luego disminuye a un mínimo en 12 coma 6.5 antes de aumentar nuevamente. Se dibuja una línea horizontal en la línea media en y es igual a 12.25, y la distancia desde la línea media hasta el punto más alto se etiqueta como 3.75.$

Con un mínimo de 8.5 y un máximo de 16, la línea media estará a medio camino entre estos valores, en

\[\dfrac{16+8.5}{2} =12.25.\nonumber\]

La amplitud será la mitad de la diferencia entre los valores más altos y más bajos:

\[\dfrac{16-8.5}{2} =3.75\nonumber\]

o equivalentemente la distancia desde la línea media hasta el valor alto o bajo, 16-12.25=3.75.

Dejando que enero sea$t = 0$, la gráfica comienza en el valor más bajo, por lo que se puede modelar como una gráfica de coseno volteado. Armando esto, obtenemos un modelo:

\[h(t)=-3.75\cos \left(\dfrac{\pi }{6} t\right)+12.25\nonumber\]

$h(t)$es nuestro modelo para horas de luz diurna t meses después de enero.

Para encontrar cuándo habrá 14 horas de luz diurna, resolvemos$h(t) = 14$.

\[14=-3.75\cos \left(\dfrac{\pi }{6} t\right)+12.25\nonumber\]Aislar el coseno
\[1.75=-3.75\cos \left(\dfrac{\pi }{6} t\right)\nonumber\] Restando 12.25 y dividiendo por -3.75
\[-\dfrac{1.75}{3.75} =\cos \left(\dfrac{\pi }{6} t\right)\nonumber\] Usando la
\[\dfrac{\pi }{6} t=\cos ^{-1} \left(-\dfrac{1.75}{3.75} \right)\approx 2.0563\nonumber\] multiplicación inversa por la recíproca
\[t=2.0563\cdot \dfrac{6}{\pi } =3.927\nonumber\]

$t=3.927$meses pasados enero

Habrá 14 horas de luz natural 3.927 meses en el año, o cerca de finales de abril.

Si bien habría una segunda vez en el año cuando hay 14 horas de luz del día, ya que estamos plantando un jardín, querríamos conocer la primera solución, en primavera, por lo que no necesitamos encontrar la segunda solución en este caso.

Ejercicio$\PageIndex{2}$

Aquí se muestra el uso mensual de gas del autor (en termas). Encuentra una función para modelar los datos.

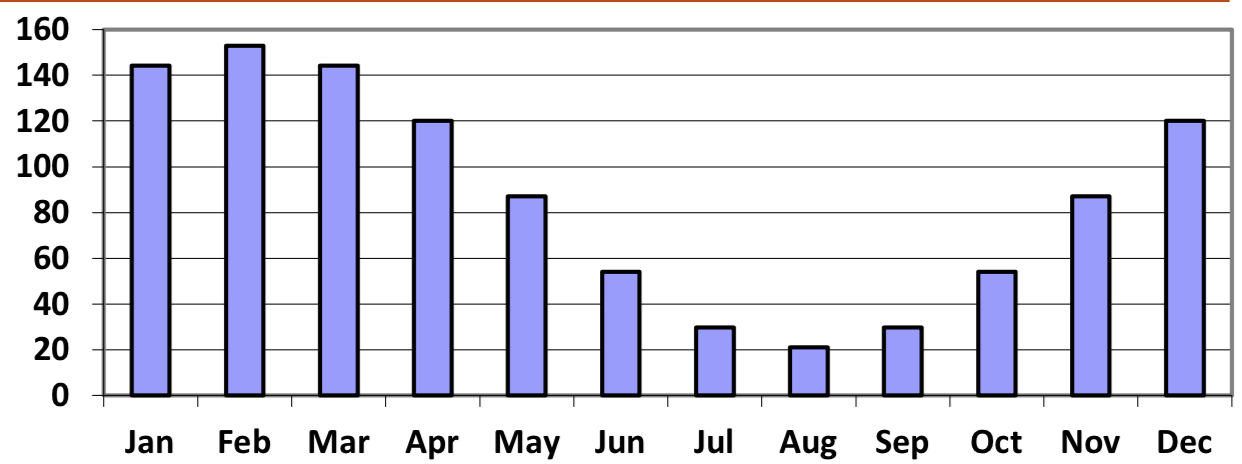
$Un gráfico de barras que muestra el uso de energía a lo largo del año, que aparece sinusoidal. El máximo de alrededor de 150 ocurre en febrero, y el mínimo de alrededor de 20 ocurre en agosto.$

Contestar: Aproximadamente\[G(t)=66\cos \left(\dfrac{\pi }{6} (t-1)\right)+87\nonumber\]

Ejemplo$\PageIndex{6}$

Un objeto se conecta a la pared con un resorte que tiene una longitud natural de 20 cm. El objeto se tira hacia atrás 8 cm más allá de la longitud natural y se libera. El objeto oscila 3 veces por segundo. Encuentra una ecuación para la posición horizontal del objeto ignorando los efectos de la fricción. ¿Cuánto tiempo durante cada ciclo está el objeto a más de 27 cm de la pared?

$Una imagen de una pared a la izquierda, un carro rodante a la derecha y un resorte horizontal que los conecta.$

Solución

Si usamos la distancia desde la pared,$x$, como salida deseada, entonces el objeto oscilará por igual a cada lado de la longitud natural del muelle de 20, poniendo la línea media de la función en 20 cm.

Si soltamos el objeto 8 cm más allá de la longitud natural, la amplitud de la oscilación será de 8 cm.

Estamos comenzando en el valor más grande y así esta función se puede modelar más fácilmente usando una función coseno.

Dado que el objeto oscila 3 veces por segundo, tiene una frecuencia de 3 y el periodo de una oscilación es 1/3 de segundo. Usando esto encontramos la compresión horizontal usando las proporciones de los periodos:$\dfrac{2\pi }{1/3} =6\pi$.

Usando todo esto, podemos construir nuestro modelo:

\[x(t)=8\cos \left(6\pi {\kern 1pt} t\right)+20 \nonumber\]

Para encontrar cuando el objeto está a 27 cm de la pared, podemos resolver$x(t) = 27$

\[27=8\cos \left(6\pi {\kern 1pt} t\right)+20\nonumber\]Aislar el coseno
\[7=8\cos \left(6\pi {\kern 1pt} t\right)\nonumber\]
\[\dfrac{7}{8} =\cos \left(6\pi {\kern 1pt} t\right)\nonumber\] usando la inversa
\[6\pi {\kern 1pt} t=\cos ^{-1} \left(\dfrac{7}{8} \right)\approx 0.505\nonumber\]
\[t=\dfrac{0.505}{6\pi } =0.0268\nonumber\]

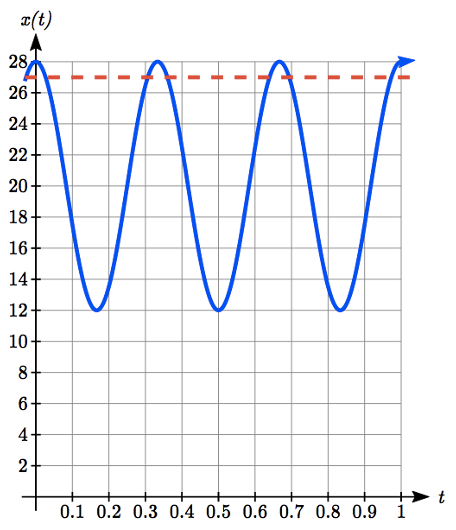
$Se dibuja un gráfico de coseno que muestra tres oscilaciones de t igual a 0 a t es igual a 1, la primera oscilación comienza en el punto más alto en 0 coma 28, disminuyendo a un mínimo en una sexta coma 12, y aumentando de nuevo a un alto en un tercio coma 28. Se dibuja una línea horizontal a 27, la cual cruza la gráfica coseno 6 veces.$

Con base en la forma de la gráfica, podemos concluir que el objeto pasará los primeros 0.0268 segundos a más de 27 cm de la pared. Con base en la simetría de la función, el objeto pasará otros 0.0268 segundos más de 27 cm de la pared al final del ciclo. En total, el objeto gasta 0.0536 segundos cada ciclo a una distancia mayor a 27 cm de la pared.

En algunos problemas, podemos usar funciones trigonométricas para modelar comportamientos más complicados que la función sinusoidal básica.

Ejemplo$\PageIndex{7}$

Una varilla rígida con longitud de 10 cm se une a un círculo de radio de 4 cm en el punto$A$ como se muestra aquí. El punto$B$ es capaz de moverse libremente a lo largo del eje horizontal, impulsando un pistón (Para una animación de esta situación, consulte www.mathdemos.org/mathdemos/s... pp/engine1.gif). Si la rueda gira en sentido antihorario a 5 revoluciones por segundo, encuentre la ubicación del punto$B$ en función del tiempo. ¿Cuándo estará el punto$B$ a 12 cm del centro del círculo?

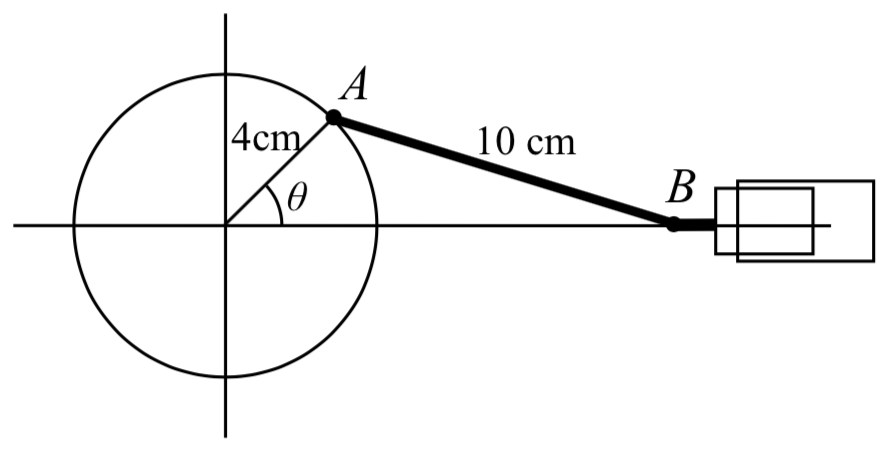
$Un círculo con radio de 4 centímetros centrado en el origen, con una línea en ángulo theta que se encuentra con el círculo en el punto A. Una línea con longitud de 10 centímetros se dibuja de A a un punto B a la derecha del círculo en el eje horizontal.$

Solución

Para encontrar la posición del punto$B$, podemos comenzar por encontrar las coordenadas del punto$A$. Ya que es un punto en un círculo con radio 4, podemos expresar sus coordenadas como$(4\cos (\theta ),4\sin (\theta ))$, donde$\theta$ se muestra el ángulo.

La velocidad angular es de 5 revoluciones por segundo, o equivalentemente 10$\pi $ radianes por segundo. Después de$t$ segundos, la rueda girará$\theta =10\pi {\kern 1pt} t$ radianes. Sustituyendo esto, podemos encontrar las coordenadas de$A$ en términos de$t$.

\[(4\cos (10\pi {\kern 1pt} t),4\sin (10\pi {\kern 1pt} t))\nonumber\]

Observe que este es el mismo valor que habríamos obtenido al observar que el periodo de la rotación es 1/5 de segundo y calculando el factor de estiramiento/compresión:

\[\dfrac{"original"}{"new"}\dfrac{2\pi}{1/5} = 10 \pi\nonumber\]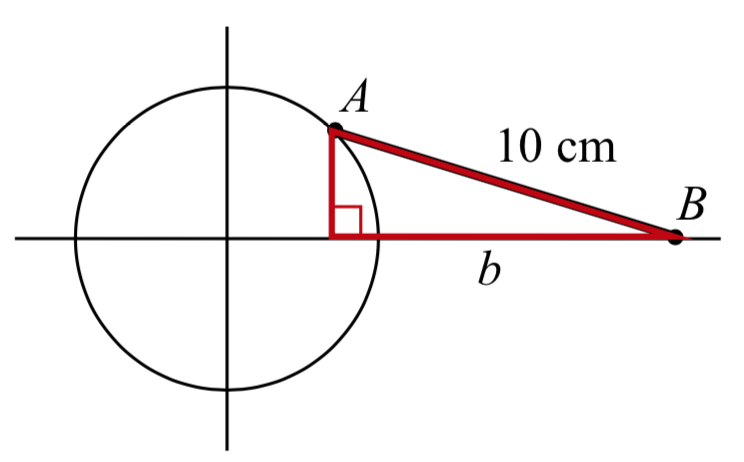 $Un círculo centrado en el origen, con un punto en el círculo etiquetado A en el primer cuadrante, y una longitud de línea 10 que conecta A a un punto B en el eje horizontal a la derecha del círculo. Se dibuja una línea vertical desde A hacia abajo hasta el eje horizontal, y una línea horizontal se dibuja desde allí hasta el punto B, con longitud etiquetada como b.$

Ahora que tenemos las coordenadas del punto$A$, podemos relacionar esto con el punto$B$. Al dibujar un segmento de línea vertical desde$A$ el eje horizontal, podemos formar un triángulo rectángulo. La altura del triángulo es la$y$ coordenada del punto$A$:\[4\sin (10\pi {\kern 1pt} t)\nonumber\]

Usando el Teorema de Pitágoras, podemos encontrar la longitud base del triángulo:

\[\left(4\sin (10\pi {\kern 1pt} t)\right)^{2} +b^{2} =10^{2}\nonumber\]
\[b^{2} =100-16\sin ^{2} (10\pi {\kern 1pt} t)\nonumber\]
\[b=\sqrt{100-16\sin ^{2} (10\pi {\kern 1pt} t)}\nonumber\]

Mirando la$x$ coordenada del punto$A$, podemos ver que el triángulo que dibujamos se desplaza a la derecha del$y$ eje por$4\cos (10\pi {\kern 1pt} t)$. Combinando este desfase con la longitud de la base del triángulo da la$x$ coordenada del punto$B$:

\[x(t)=4\cos (10\pi {\kern 1pt} t)+\sqrt{100-16\sin ^{2} (10\pi {\kern 1pt} t)}\nonumber\]

Para resolver para cuando el punto B estará a 12 cm del centro del círculo, necesitamos resolverlo$x(t) = 12$.

\[12=4\cos (10\pi {\kern 1pt} t)+\sqrt{100-16\sin ^{2} (10\pi {\kern 1pt} t)}\nonumber\]Aislar la raíz
\[12-4\cos (10\pi {\kern 1pt} t)=\sqrt{100-16\sin ^{2} (10\pi {\kern 1pt} t)}\nonumber\] cuadrada Cuadrar ambos lados
\[\left(12-4\cos (10\pi {\kern 1pt} t)\right)^{2} =100-16\sin ^{2} (10\pi {\kern 1pt} t)\nonumber\] Expandir el lado izquierdo
\[144-96\cos (10\pi {\kern 1pt} t)+16\cos ^{2} (10\pi {\kern 1pt} t)=100-16\sin ^{2} (10\pi {\kern 1pt} t)\nonumber\] Mover todos los términos a la izquierda
\[44-96\cos (10\pi {\kern 1pt} t)+16\cos ^{2} (10\pi {\kern 1pt} t)+16\sin ^{2} (10\pi {\kern 1pt} t)=0\nonumber\] Facturar hacia fuera 16
\[44-96\cos (10\pi {\kern 1pt} t)+16\left(\cos ^{2} (10\pi {\kern 1pt} t)+\sin ^{2} (10\pi {\kern 1pt} t)\right)=0\nonumber\]

En este punto, podemos utilizar la Identidad Pitagórica, que nos dice que

\[\cos ^{2} (10\pi {\kern 1pt} t)+\sin ^{2} (10\pi {\kern 1pt} t)=1\nonumber\]

Usando esta identidad, nuestra ecuación simplifica

\[44-96\cos (10\pi {\kern 1pt} t)+16=0\nonumber\]Combinar las constantes y moverse hacia el lado derecho
\[-96\cos (10\pi {\kern 1pt} t)=-60\nonumber\] Dividir
\[\cos (10\pi {\kern 1pt} t)=\dfrac{60}{96}\nonumber\] Hacer una sustitución
\[\cos (u)=\dfrac{60}{96}\nonumber\]
\[u=\cos ^{-1} \left(\dfrac{60}{96} \right)\approx 0.896\nonumber\] Por simetría podemos encontrar una segunda solución
\[u=2\pi -0.896=5.388\nonumber\] Deshaciendo la sustitución

\[10\pi {\kern 1pt} t=0.896\text{, so }t = 0.0285\nonumber\]
\[10\pi {\kern 1pt} t=5.388\text{, so }t = 0.1715\nonumber\]

El punto$B$ estará a 12 cm del centro del círculo 0.0285 segundos después de que comience el proceso, 0.1715 segundos después de que comience el proceso, y cada 1/5 de segundo después de cada uno de esos valores.

Temas Importantes de esta Sección

Modelado con ecuaciones trig
Modelado con funciones sinusoidales
Resolviendo triángulos rectos para ángulos en grados y radianes