Saltar al contenido principal
LibreTexts Español

9.1.1E: Elipses (Ejercicios)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    116779

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    ejercicios de la sección 9.1

    En los problemas 1—4, empareja cada gráfica con una de las ecuaciones A—D.
    A.\(\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1\)

    B.\(\dfrac{x^2}{9} + \dfrac{y^2}{4} = 1\)

    C.\(\dfrac{x^2}{9} + {y^2} = 1\)

    D.\({x^2} + \dfrac{y^2}{9} = 1\)

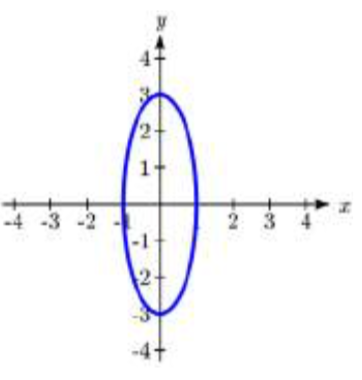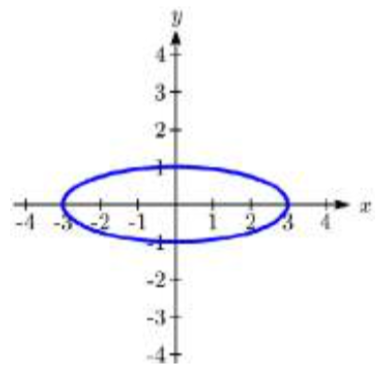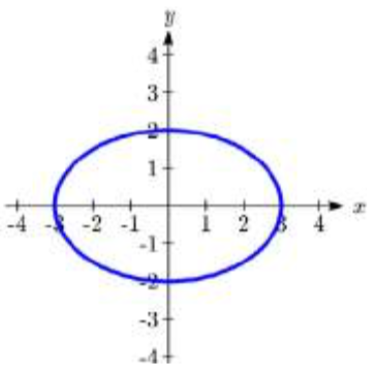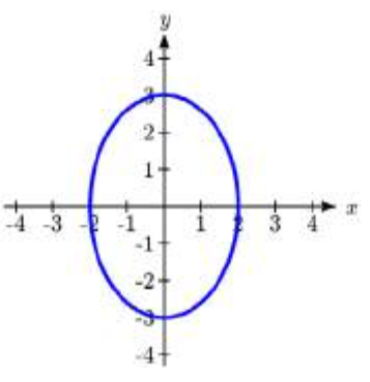
    1. 2019-07-30 12.53.34.png2. 2019-07-30 12.53.52.png3. 2019-07-30 12.54.34.png4. 2019-07-30 12.55.27.png

    En los problemas 5—14, encuentre los vértices, los extremos del eje menor, la longitud del eje mayor y la longitud del eje menor. Esbozar la gráfica. Verifique usando una utilidad gráfica.
    5. \(\dfrac{x^2}{4} + \dfrac{y^2}{25} = 1\)

    6. \(\dfrac{x^2}{16} + \dfrac{y^2}{4} = 1\)

    7. \(\dfrac{x^2}{4} + y^2 = 1\)

    8. \(x^2 + \dfrac{y^2}{25} = 1\)

    9. \(x^2+ 25y^2 = 25\)

    10. \(16x^2 + y^2 = 16\)

    11. \(16x^2 + 9y^2 = 144\)

    12. \(16x^2 + 25y^2 = 400\)

    13. \(9x^2 + y^2 = 18\)

    14. \(x^2 + 4y^2 = 12\)

    En los problemas 15—16, escriba una ecuación para la gráfica.

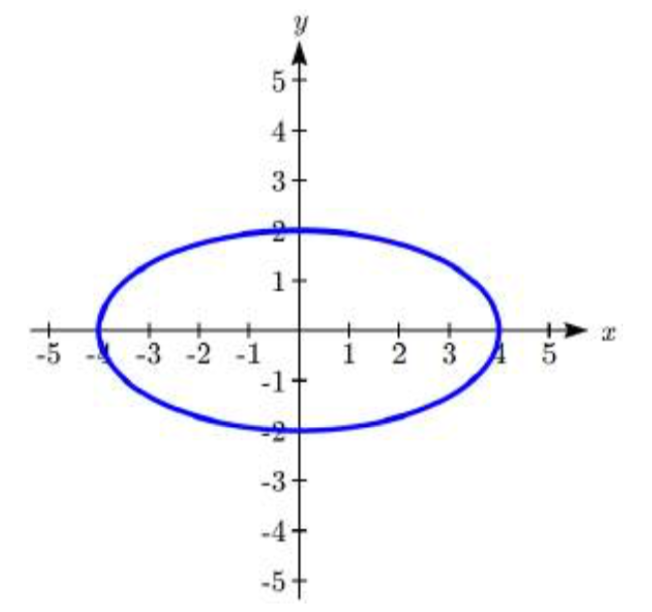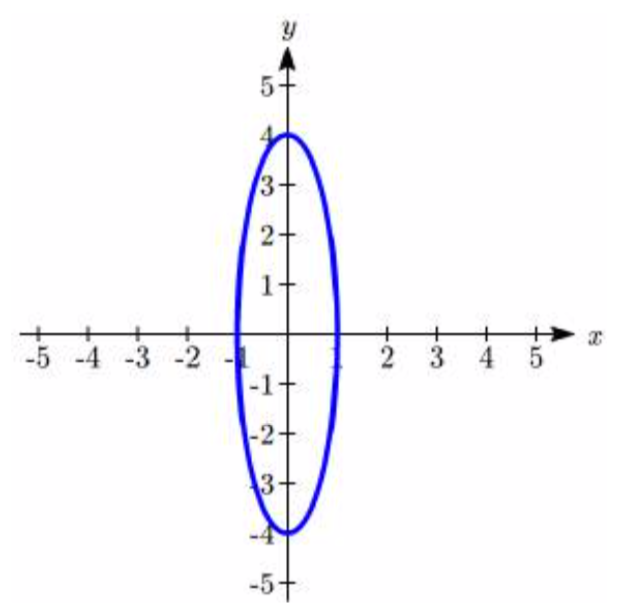
    15. 2019-07-30 12.56.57.png16. 2019-07-30 12.57.36.png

    En los problemas 17—20, encuentra la forma estándar de la ecuación para una elipse que satisface las condiciones dadas.

    17. Centro (0,0), longitud del eje mayor horizontal 64, longitud del eje menor 14

    18. Centro (0,0), longitud del eje mayor vertical 36, longitud del eje menor 18

    19. Centro (0,0), vértice (0,3),\(b = 2\)

    20. Centro (0,0), vértice (4,0),\(b = 3\)

    En los problemas 21—28, haga coincidir cada gráfica con las ecuaciones A-H.
    A.\(\dfrac{\left( {x - 2} \right)^2}{4} + \dfrac{{(y - 1)}^2}{9} = 1\)

    E.\(\dfrac{\left( {x + 2} \right)^2}{4} + \dfrac{{(y + 1)}^2}{9} = 1\)
    B.\(\dfrac{\left( {x - 2} \right)^2}{4} + \dfrac{{(y - 1)}^2}{16} = 1\)

    F.\(\dfrac{\left( {x + 2} \right)^2}{4} + \dfrac{{(y + 1)}^2}{16} = 1\)
    C.\(\dfrac{\left( {x - 2} \right)^2}{16} + \dfrac{{(y - 1)}^2}{4} = 1\)

    G.\(\dfrac{\left( {x + 2} \right)^2}{16} + \dfrac{{(y + 1)}^2}{4} = 1\)
    D.\(\dfrac{\left( {x - 2} \right)^2}{9} + \dfrac{{(y - 1)}^2}{4} = 1\)

    H.\(\dfrac{\left( {x + 2} \right)^2}{9} + \dfrac{{(y + 1)}^2}{4} = 1\)

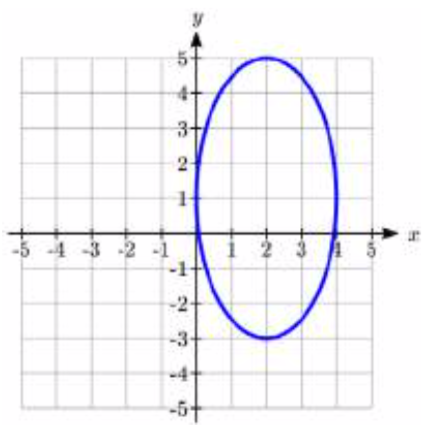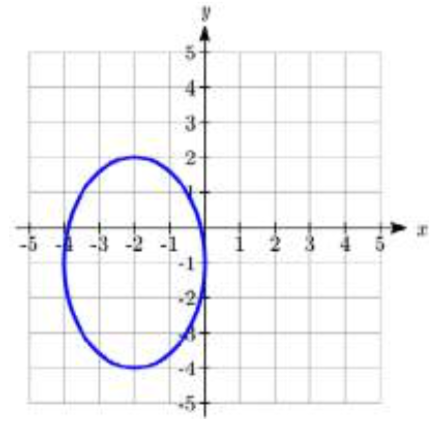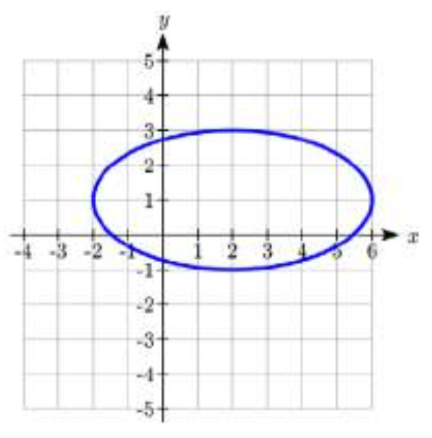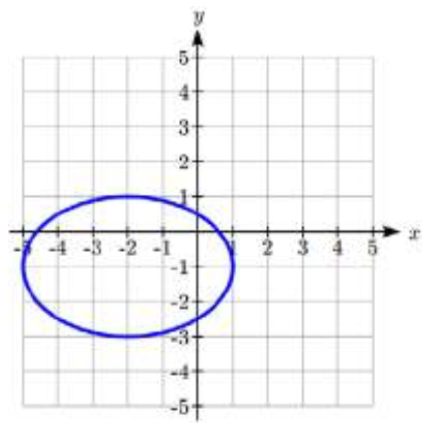
    21. 2019-07-30 12.59.57.png22. 2019-07-30 1.01.19.png23. 2019-07-30 1.02.03.png24. 2019-07-30 1.02.24.png

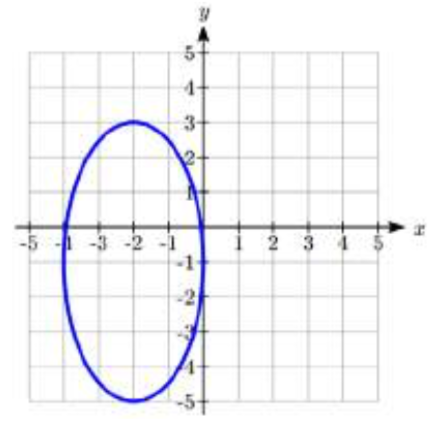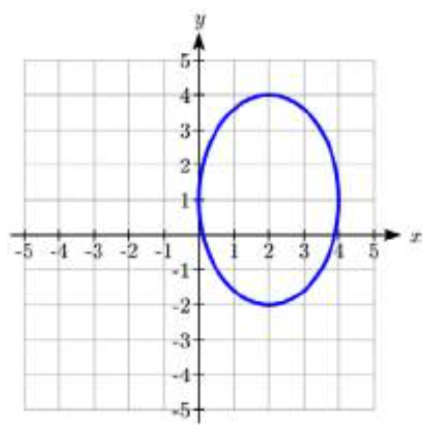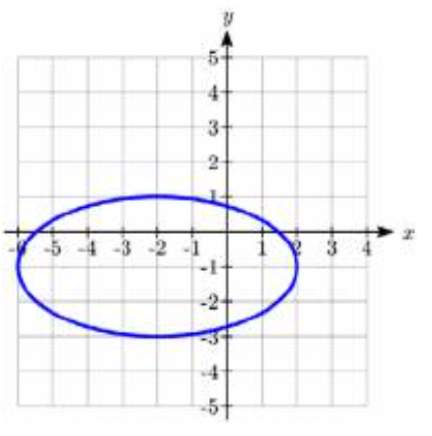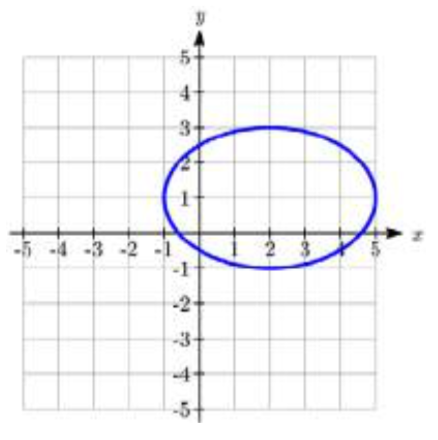
    25. 2019-07-30 1.02.44.png26. 2019-07-30 1.03.28.png27. 2019-07-30 1.04.09.png28. 2019-07-30 1.04.30.png

    En los problemas 29—38, encuentre los vértices, los extremos del eje menor, la longitud del eje mayor y la longitud del eje menor. Esbozar la gráfica. Verifique usando una utilidad gráfica.

    29. \(\dfrac{(x - 1)^2}{25} + \dfrac{(y + 2)^2}{4} = 1\)

    30. \(\dfrac{(x + 5)^2}{16} + \dfrac{(y - 3)^2}{36} = 1\)

    31. \((x + 2)^2 + \dfrac{(y - 3)^2}{25} = 1\)

    32. \(\dfrac{(x - 1)^2}{25} + (y - 6)^2 = 1\)

    33. \(4x^2 + 8x + 4 + y^2 = 16\)

    34. \(x^2 + 4y^2 + 16y + 16 = 36\)

    35. \(x^2 + 2x + 4y^2 + 16y = - 1\)

    36. \(4x^2 + 16x + y^2 - 8y = 4\)

    37. \(9x^2 - 36x + 4y^2 + 8y = 104\)

    38. \(4x^2 + 8x + 9y^2 + 36y = - 4\)

    En los problemas 39—40, escriba una ecuación para la gráfica.

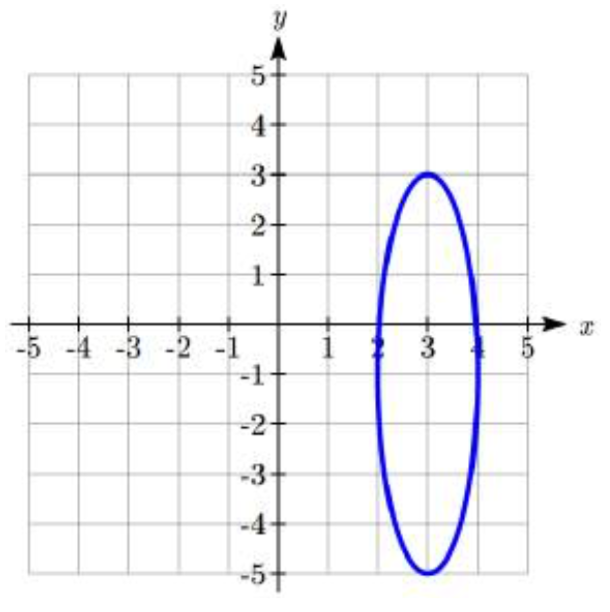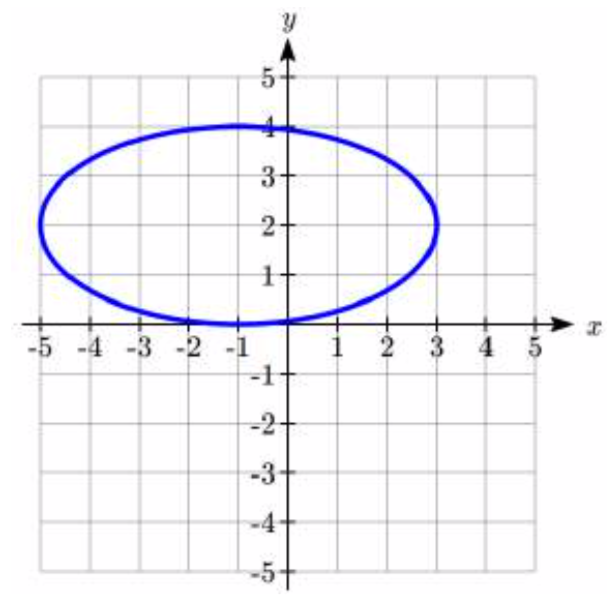
    39. 2019-07-30 1.06.55.png40. 2019-07-30 1.07.24.png

    En los problemas 41—42, encuentra la forma estándar de la ecuación para una elipse que satisface las condiciones dadas.

    41. Centro (-4, 3), vértice (-4, 8), punto en la gráfica (0, 3)

    42. Centro (1, -2), vértice (-5, -2), punto en la gráfica (1, 0)

    43. Ventana Una ventana en forma de semielipse mide 12 pies de ancho y 4 pies de alto. ¿Cuál es la altura de la ventana por encima de la base a 5 pies del centro?

    44. Ventana Una ventana en forma de semielipse tiene 16 pies de ancho y 7 pies de alto. ¿Cuál es la altura de la ventana por encima de la base a 4 pies del centro?

    45. Puente Un puente sobre un río está sostenido por un arco semielíptico. El río tiene 150 pies de ancho. En el centro, el arco se eleva a 60 pies sobre el río. La calzada está a 5 pies por encima del centro del arco. ¿Cuál es la distancia vertical entre la calzada y el arco a 45 pies del centro?

    46. Puente Un puente sobre un río está sostenido por un arco semielíptico. El río tiene 1250 pies de ancho. En el centro, el arco se eleva a 175 pies sobre el río. La calzada está a 3 pies por encima del centro del arco. ¿Cuál es la distancia vertical entre la calzada y el arco a 600 pies del centro?

    47. Pista de carreras Una pista de carreras elíptica mide 100 pies de largo y 90 pies de ancho. ¿Cuál es el ancho de la pista de carreras a 20 pies de un vértice en el eje mayor?

    48. Pista de carreras Una pista de carreras elíptica mide 250 pies de largo y 150 pies de ancho. ¿Cuál es el ancho de la pista a 25 pies de un vértice en el eje mayor?

    En los problemas 49-52, encuentra los focos.

    49. \(\dfrac{x^2}{19} + \dfrac{y^2}{3} = 1\)50. \(\dfrac{x^2}{2} + \dfrac{y^2}{38} = 1\)

    51. \((x + 6)^2 + \dfrac{(y - 1)^2}{26} + = 1\)52. \(\dfrac{(x - 3)^2}{10} + (y + 5)^2 = 1\)

    En los problemas 53-72, encuentra la forma estándar de la ecuación para una elipse que satisface las condiciones dadas.

    53. Vértices de eje mayor (\(\pm\)3,0),\(c= 2\)

    54. Vértices de eje mayor (0,\(\pm\) 7),\(c= 4\)

    55. Focos (0,\(\pm\) 5) y longitud del eje mayor 12

    56. Focos (\(\pm\)3, 0) y longitud del eje mayor 8

    57. Focos (\(\pm\)5, 0), vértices (\(\pm\)7, 0)

    58. Focos (0,\(\pm\) 2), vértices (0,\(\pm\) 3)

    59. Focos (0,\(\pm\) 4) e\(x\) -intercepciones (\(\pm\)2, 0)

    60. Focos (\(\pm\)3, 0) e\(y\) -intercepciones (0,\(\pm\) 1)

    61. Centro (0, 0), longitud del eje mayor 8, focos en el\(x\) eje, pasa a través del punto\(\left( 2,\sqrt 6 \right)\)

    62. Centro (0, 0), longitud del eje mayor 12, focos en el\(y\) eje, pasa a través del punto\(\left( \sqrt {10} ,4 \right)\)

    63. Centro (-2, 1), vértice (-2, 5), foco (-2, 3)

    64. Centro (-1, -3), vértice (-7, -3), enfoque (-4, -3)

    65. Focos (8, 2) y (-2, 2), longitud del eje mayor 12

    66. Focos (-1, 5) y (-1, -3), longitud del eje mayor 14

    67. Vértices (3, 4) y (3, -6),\(c= 2\)

    68. Vértices (2, 2) y (-4, 2),\(c= 2\)

    69. Centro (1, 3), foco (0, 3), pasa a través del punto (1, 5)

    70. Centro (-1, -2), foco (1, -2), pasa a través del punto (2, -2)

    71. Enfoque (-15, -1), vértices (-19, -1) y (15, -1)

    72. Foco (-3, 2), vértices (-3, 4) y (-3, -8)

    73. Galería Susurrante Si una galería elíptica susurrante mide 80 pies de largo y 25 pies de ancho, ¿a qué distancia del centro de la habitación debería alguien pararse en el eje mayor de la elipse para experimentar el efecto susurrante? Redondear a dos decimales.

    74. Billar Algunas mesas de billar son elípticas y tienen los focos marcados en la mesa. Si tal uno mide 8 pies de largo y 6 pies de ancho, ¿qué tan lejos están los focos del centro de la elipse? Redondear a dos decimales.

    75. Órbitas planetarias Las órbitas de los planetas alrededor del sol son aproximadamente elípticas con el sol como foco. El afelio es la mayor distancia de un planeta del sol y el perihelio es su más corto. La longitud del eje mayor es la suma del afelio y del perihelio. El afelio de la Tierra es de 94.51 millones de millas y su perihelio es de 91.40 millones de millas. Escribe una ecuación para la órbita de la Tierra.

    76. Órbitas satelitales La órbita de un satélite alrededor de la Tierra es elíptica con el centro de la Tierra como foco. La altura máxima del satélite sobre la Tierra es de 170 millas y su altura mínima sobre la Tierra es de 90 millas. Escribe una ecuación para la órbita del satélite. Supongamos que la Tierra es esférica y tiene un radio de 3960 millas.

    77. La excentricidad\(e\) de una elipse es la relación\(\dfrac{c}{a}\) donde\(c\) está la distancia de un foco desde el centro y a es la distancia de un vértice desde el centro. Escribe una ecuación para una elipse con excentricidad 0.8 y focos en (-4, 0) y (4, 0).

    78. Las elipses confocales tienen los mismos focos. Mostrar que, para\(k > 0\), todas las elipses de la forma\(\dfrac{x^2}{6 + k} + \dfrac{y^2}{k} = 1\) son confocales.

    79. El recto latus de una elipse es un segmento lineal con puntos finales en la elipse que pasa a través de un foco y es perpendicular al eje mayor. Demostrar que\(\dfrac{2b^2}{a}\) es la longitud del recto latus de\(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) donde\(a > b\).

    Contestar

    1. D

    3. B

    5. Vértices\((0, \pm 5)\), extremos del eje menor\((\pm 2, 0)\), longitud mayor = 10, longitud menor = 4

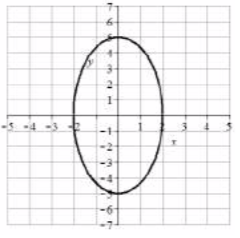
    Screen Shot 2019-10-17 en 7.58.53 AM.png

    7. Vértices\((\pm 5, 0)\), extremos del eje menor\((0, \pm 1)\), longitud mayor = 4, longitud menor = 2

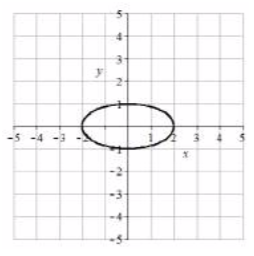
    Screen Shot 2019-10-17 a las 7.59.37 AM.png

    9. Vértices\((\pm 5, 0)\), extremos del eje menor\((0, \pm 1)\), longitud mayor = 10, longitud menor = 2

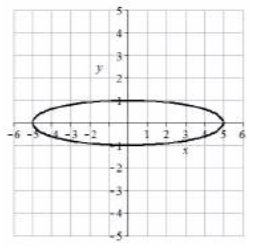
    Screen Shot 2019-10-17 a las 8.00.37 AM.png

    11. Vértices\((0, \pm 4)\), extremos del eje menor\((\pm 3, 0)\), longitud mayor = 8, longitud menor = 6

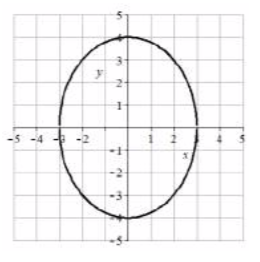
    Screen Shot 2019-10-17 a las 8.01.19 AM.png

    13. Vértices\((0, \pm 3\sqrt{2})\), extremos del eje menor\((\pm \sqrt{2}, 0)\), longitud mayor =\(6\sqrt{2}\), longitud menor =\(2\sqrt{2}\)

    Screen Shot 2019-10-17 en 8.02.06 AM.png

    15. \(\dfrac{x^2}{16} + \dfrac{y^2}{4} = 1\)

    17. \(\dfrac{x^2}{1024} + \dfrac{y^2}{49} = 1\)

    19. \(\dfrac{x^2}{4} + \dfrac{y^2}{9} = 1\)

    21. B

    23. C

    25. F

    27. G

    29. Centro (1, -2), vértices (6, -2) y (-4, -2), extremos del eje menor (1, 0) y (1, -4), longitud mayor= 10, longitud menor = 4

    Screen Shot 2019-10-17 en 8.03.50 AM.png

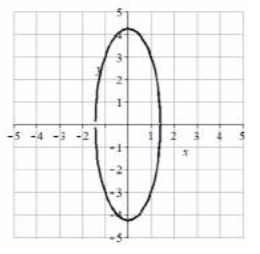
    31. Centro (-2, 3), vértices (-2, 8) y (-2, -2), extremos del eje menor (-1, 3) y (-3, 3), longitud mayor = 10, longitud menor = 2

    Screen Shot 2019-10-17 en 8.04.27 AM.png

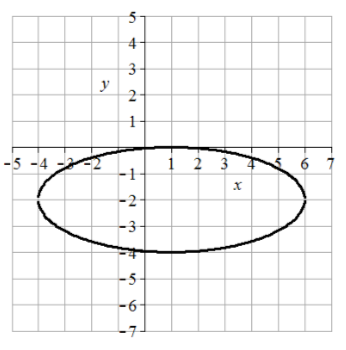
    33. Centro (-1, 0), vértices (-1, 4) y (-1, -4), extremos del eje menor (-1, 0) y (3, 0), longitud mayor = 8, longitud menor = 4

    Screen Shot 2019-10-17 en 8.05.06 AM.png

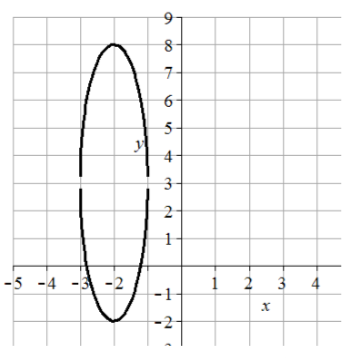
    35. Centro (-1, -2), vértices (3, -2) y (-5, -2), extremos del eje menor (-1, 0) y (-1, -4), longitud mayor = 8, longitud menor = 4

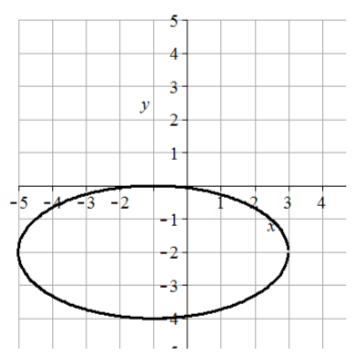
    Screen Shot 2019-10-17 en 8.05.40 AM.png

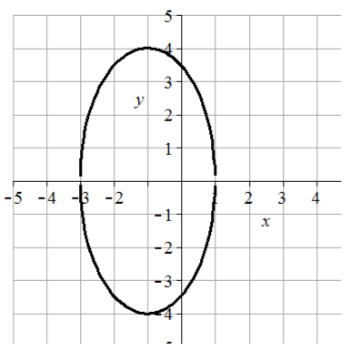
    37. Centro (2, -1), vértices (2, 5) y (2, -7), extremos de eje menor (6, -1) y (-2, -1), longitud mayor = 12, longitud menor = 8

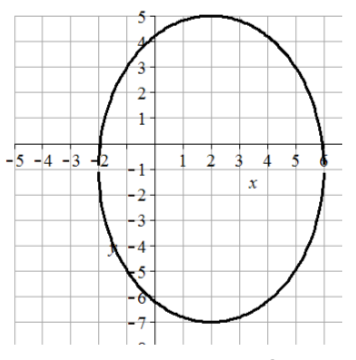
    Screen Shot 2019-10-17 a las 8.06.09 AM.png

    39. \((x - 3)^2 + \dfrac{(y + 1)^2}{16} = 1\)

    41. \(\dfrac{(x + 4)^2}{16} + \dfrac{(y - 3)^2}{25} = 1\)

    43. 2.211083 pies

    45. 17 pies

    47. 64 pies

    49. \((\pm 4, 0)\)

    51. (-6, 6) y (-6, -4)

    53. \(\dfrac{x^2}{9} + \dfrac{y^2}{5} = 1\)

    55. \(\dfrac{x^2}{11} + \dfrac{y^2}{36} = 1\)

    57. \(\dfrac{x^2}{49} + \dfrac{y^2}{24} = 1\)

    59. \(\dfrac{x^2}{4} + \dfrac{y^2}{20} = 1\)

    61. \(\dfrac{x^2}{16} + \dfrac{y^2}{8} = 1\)

    63. \(\dfrac{(x + 2)^2}{12} + \dfrac{(y - 1)^2}{16} = 1\)

    65. \(\dfrac{(x - 3)^2}{36} + \dfrac{(y - 2)^2}{11} = 1\)

    67. \(\dfrac{(x - 3)^2}{21} + \dfrac{(y + 1)^2}{25} = 1\)

    69. \(\dfrac{(x - 1)^2}{4} + \dfrac{(y - 3)^2}{5} = 1\)

    71. \(\dfrac{(x + 2)^2}{289} + \dfrac{(y + 1)^2}{120} = 1\)

    73. 31.22 pies

    75. \(\dfrac{x^2}{8640.632025} + \dfrac{y^2}{8638.214} = 1\)

    77. \(\dfrac{x^2}{25} + \dfrac{y^2}{9} = 1\)

    79. El centro está en (0, 0). Ya que\(a > b\), la elipse es horizontal. Sea (\(c\), 0) el foco en el eje x positivo. Let (\(c, h\)) ser el punto final en el Cuadrante 1 del recto latus que pasa por (\(c\),0).

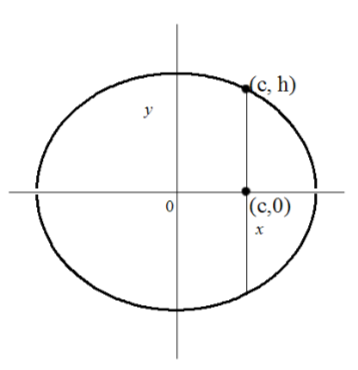
    Screen Shot 2019-10-17 a las 8.25.17 AM.png

    La distancia entre el foco y el punto final del recto latus se puede encontrar sustituyendo (\(c\),0) y\((c,h)\) en la fórmula de distancia\(h = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\) que rinde\(h = \sqrt{(c - c)^2 + (h - 0)^2} = h\). Así\(h\) es la mitad de la distancia del recto latus. Sustituir (\(c\),\(h\)) en la ecuación de elipse para encontrar\(h\) da\(\dfrac{c^2}{a^2} + \dfrac{h^2}{b^2} = 1\). Resolver por\(h\) rendimientos\(h^2 = b^2(1 - \dfrac{c^2}{a^2}) = b^2 (\dfrac{a^2}{a^2} - \dfrac{c^2}{a^2}) = b^2 (\dfrac{a^2 - c^2}{a^2}) = b^2(\dfrac{b^2}{a^2}) = \dfrac{b^4}{a^2}\). entonces\(h = \sqrt{\dfrac{b^4}{a^2}} = \dfrac{b^2}{a}\). La distancia del recto latus es\(2h = \dfrac{2b^2}{a}\).

    9.1.1E: Elipses (Ejercicios) is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.