9.2: Hipérbolas
- Page ID
- 116789
En la última sección, aprendimos que los planetas tienen órbitas aproximadamente elípticas alrededor del sol. Cuando un objeto como un cometa se mueve rápidamente, es capaz de escapar de la atracción gravitacional del sol y sigue un camino con la forma de una hipérbola. Las hipérbolas son curvas que pueden ayudarnos a encontrar la ubicación de un barco, describir la forma de las torres de enfriamiento o calibrar equipos sismológicos.
rápidamente, es capaz de escapar de la atracción gravitacional del sol y sigue un camino con la forma de una hipérbola. Las hipérbolas son curvas que pueden ayudarnos a encontrar la ubicación de un barco, describir la forma de las torres de enfriamiento o calibrar equipos sismológicos.
La hipérbola es otro tipo de sección cónica creada al intersectar un plano con un doble cono, como se muestra a continuación (Pbroks13 (Commons.wikimedia.org/wiki/F... with_plane.svg), “Secciones cónicas con plano”, recortadas para mostrar solo una hipérbola por L Michaels, CC BY 3.0).
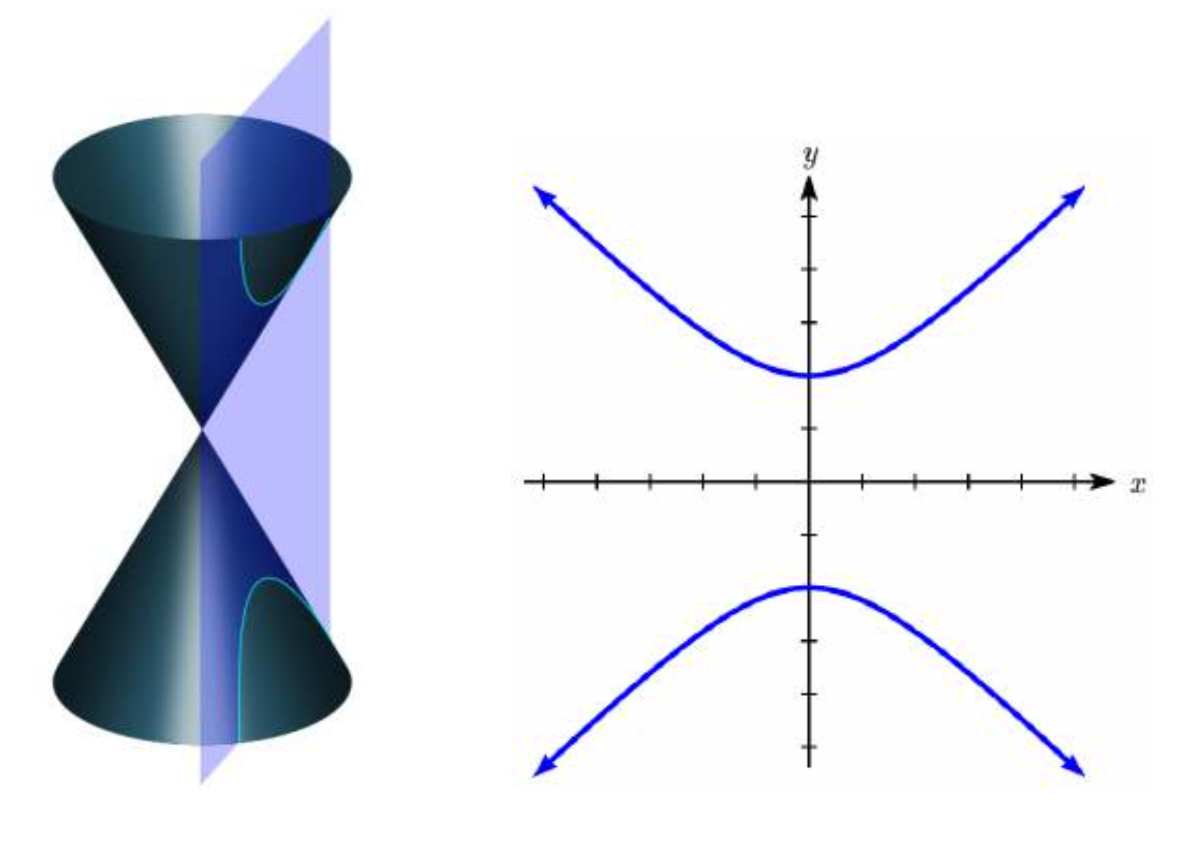
La palabra “hipérbola” deriva de una palabra griega que significa “exceso”. La palabra inglesa “hipérbole” significa exageración. Podemos pensar en una hipérbola como una elipse excesiva o exagerada, una volteada al revés.
Definimos una elipse como el conjunto de todos los puntos donde la suma de las distancias desde ese punto a dos puntos fijos es una constante. Una hipérbola es el conjunto de todos los puntos donde el valor absoluto de la diferencia de las distancias desde el punto a dos puntos fijos es una constante.
Definición: Hipérbola
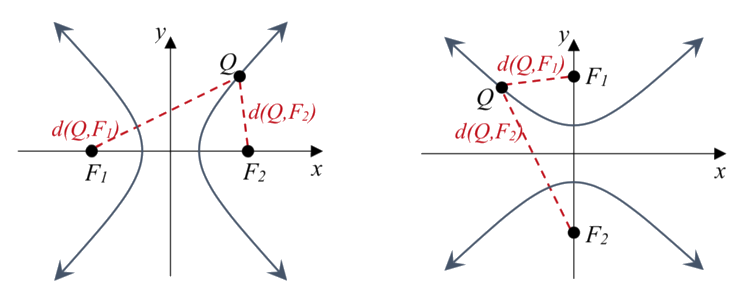
Una hipérbola es el conjunto de todos los puntos\(Q\;\left( x,y \right)\) para los cuales el valor absoluto de la diferencia de las distancias a dos puntos fijos\(F_1\left( x_1,y_1 \right)\) y\(F_2\left( x_2,y_2 \right)\) llamado los focos (plural para foco) es una constante\(k\):\[\left| {d\left( Q,F_1 \right) - d\left( Q,F_2 \right)} \right| = k\]
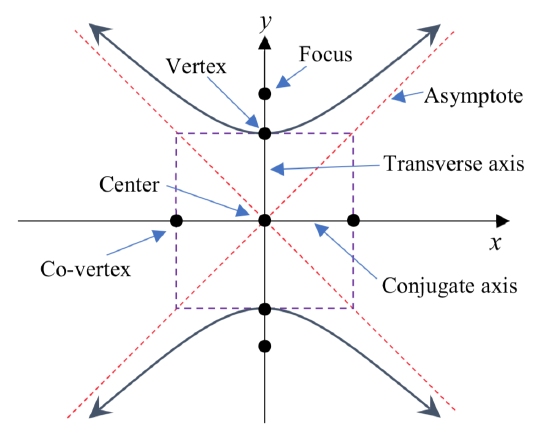
- El eje transversal es la línea que pasa por los focos.
- Los vértices son los puntos en la hipérbola que se cruzan con el eje transversal.
- La longitud del eje transversal es la longitud del segmento de línea entre los vértices.
- El centro es el punto medio entre los vértices (o el punto medio entre los focos).
- El otro eje de simetría a través del centro es el eje conjugado.
- Las dos piezas disjuntas de la curva se llaman ramas.
- Una hipérbola tiene dos asíntotas.
Qué eje es el eje transversal dependerá de la orientación de la hipérbola. Como herramienta útil para graficar hipérbolas, es común dibujar un rectángulo central como guía. Se trata de un rectángulo dibujado alrededor del centro con lados paralelos a los ejes de coordenadas que pasan por cada vértice y covértice. Las asíntotas seguirán las diagonales de este rectángulo.
Hipérbolas Centradas en el Origen
De la definición anterior podemos encontrar una ecuación de una hipérbola. Lo encontraremos para una hipérbola centrada en el origen\(C\left( 0,0 \right)\) abriendo horizontalmente con focos en
\[F_1\left( c,0 \right)\text{ and }F_2\left( - c,0 \right)\text{ where }c > 0\nonumber\]
Supongamos que\(Q\left( x,y \right)\) es un punto sobre la hipérbola. Las distancias de\(Q\) a\(F_1\) y\(Q\) a\(F_2\) son:
\[d\left( Q, F_1 \right) = \sqrt {\left( x - c \right)^2 + \left( y - 0 \right)^2} = \sqrt {\left( x - c \right)^2 + y^2} \nonumber\]
\[d\left( Q,F_2 \right) = \sqrt {\left( x - \left( - c \right) \right)^2 + \left( y - 0 \right)^2} = \sqrt {\left( x + c \right)^2 + y^2} \nonumber\]
A partir de la definición, el valor absoluto de la diferencia debe ser constante:
\[\left| d\left( Q, F_1 \right) - d\left(Q, F_2 \right) \right| = \left| \sqrt {\left( x - c \right)^2 + y^2} - \sqrt {\left( x + c \right)^2 + y^2 } \right| = k\nonumber\]
Sustituyendo en uno de los vértices\(\left( a,0 \right)\), podemos determinar\(k\) en términos de\(a\):
\[\left| \sqrt {\left( a - c \right)^2 + 0^2} - \sqrt {\left( a + c \right)^2 + 0^2 } \right| = k\nonumber\]
\[\left| \left| a - c \right| - \left| a + c \right| \right| = k\nonumber\]Dado que\(c > a\),\(\left| a - c \right| = c - a\)
\[\left| (c - a) - (a + c) \right| = k\nonumber\]
\[k = \left| - 2a \right| = \left| 2a \right|\nonumber\]
Usando\(k = 2a\) y eliminando los valores absolutos,
\[\sqrt {\left( x - c \right)^2 + y^2} - \sqrt {\left( x + c \right)^2+ y^2} = \pm 2a\nonumber\]Mover un radical
\[\sqrt {\left( x - c \right)^2 + y^2} = \pm 2a + \sqrt {\left( x + c \right)^2 + y^2} \nonumber\] Cuadrado ambos lados
\[\left( x - c \right)^2 + y^2 = 4a^2 \pm 4a\sqrt {\left( x + c \right)^2 + y^2} + \left( x + c \right)^2 + y^2\nonumber\] Expandir
\[x^2 - 2xc + c^2 + y^2 = 4a^2 \pm 4a\sqrt {\left( x + c \right)^2 + y^2} + x^2 + 2xc + c^2 + y^2\nonumber\]
Combinando términos similares hojas
\[ - 4xc = 4a^2 \pm 4a\sqrt {\left( x + c \right)^2 + y^2} \nonumber\]Dividir por 4
\[ - xc = a^2 \pm a \sqrt {\left( x + c \right)^2 + y^2} \nonumber\] Aislar el radical
\[ \pm a \sqrt {\left( x + c \right)^2 + y^2} = - a^2 - xc\nonumber\] Cuadrar ambos lados otra vez
\[a^2\left( \left( x + c \right)^2 + y^2 \right) = a^4 + 2a^2xc + x^2c^2\nonumber\] Ampliar y distribuir
\[a^2x^2 + 2a^2xc + a^2c^2 + a^2y^2 = a^4 + 2a^2xc + x^2c^2\nonumber\] Combinar términos similares
\[a^2y^2 + a^2c^2 - a^4 = x^2c^2 - a^2x^2\nonumber\] Factor términos comunes
\[a^2y^2 + a^2\left( c^2 - a^2 \right) = \left( c^2 - a^2 \right)x^2\nonumber\]
Dejar \(b^2 = c^2 - a^2\). Ya que\(c > a\),\(b > 0\). Sustitución\(b^2\) de\(c^2 - a^2\) hojas
\[a^2y^2 +a^2b^2 = b^2x^2\nonumber\] Divide ambos lados por\(a^2b^2\)
\[\dfrac{y^2}{b^2} + 1 = \dfrac{x^2}{a^2}\nonumber\] Reescritura
\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\nonumber\]
Podemos ver por las gráficas de las hipérbolas que las ramas parecen acercarse a las asíntotas a medida que\(x\) se agranda en la dirección negativa o positiva. Las ecuaciones de las asíntotas hipérbola horizontales pueden derivarse de su ecuación estándar.
\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\nonumber\]Resolver para\(y\)
\[y^2 = b^2\left( \dfrac{x^2}{a^2} - 1 \right)\nonumber\] reescribir 1 como\(\dfrac{x^2}{a^2}\dfrac{a^2}{x^2}\)
\[y^2 = b^2\left( \dfrac{x^2}{a^2} - \dfrac{x^2}{a^2}\dfrac{a^2}{x^2} \right)\nonumber\] factor de salida\(\dfrac{x^2}{a^2}\)
\[y^2 = b^2\dfrac{x^2}{a^2}\left( 1 - \dfrac{a^2}{x^2} \right)\nonumber\] Toma la raíz cuadrada
\[y = \pm \dfrac{b}{a}x\sqrt {1 - \dfrac{a^2}{x^2}} \nonumber\]
Como\(x \to \pm \infty\) la cantidad\(\dfrac{a^2}{x^2} \to 0\) y\(\sqrt {1 - \dfrac{a^2}{x^2}} \to 1\), así son las asíntotas\(y = \pm \dfrac{b}{a}x\).
De igual manera, para las hipérbolas verticales son las asíntotas\(y = \pm \dfrac{a}{b}x\).
La forma estándar de una ecuación de una hipérbola centrada en el origen C\(\left( {0,0} \right)\) depende de si se abre horizontal o verticalmente. La siguiente tabla da la ecuación estándar, vértices, focos, asíntotas, vértices de rectángulo de construcción y gráfica para cada uno.
| Abre | Horizontalmente | Verticalmente |
|---|---|---|
| Ecuación estándar | \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) | \(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\) |
| Vértices | \((-a, 0)\)y\((a, 0)\) | \((0, -a)\)y\((0, a)\) |
| Focos | \((-c, 0)\)y\((c, 0)\) donde\(b^2 = c^2 - a^2\) |
\((0, -c)\)y\((0, c)\) |
| Asíntotas | \(y = \pm \dfrac{b}{a} x\) | \(y = \pm \dfrac{a}{b} x\) |
| Construcción Rectángulo Vértices | \((a, b)\),\((-a, b)\),\((a, -b)\),\((-a, -b)\) | \((b, a)\),\((-b, a)\),\((b, -a)\),\((-b, -a)\) |
| Gráfica | 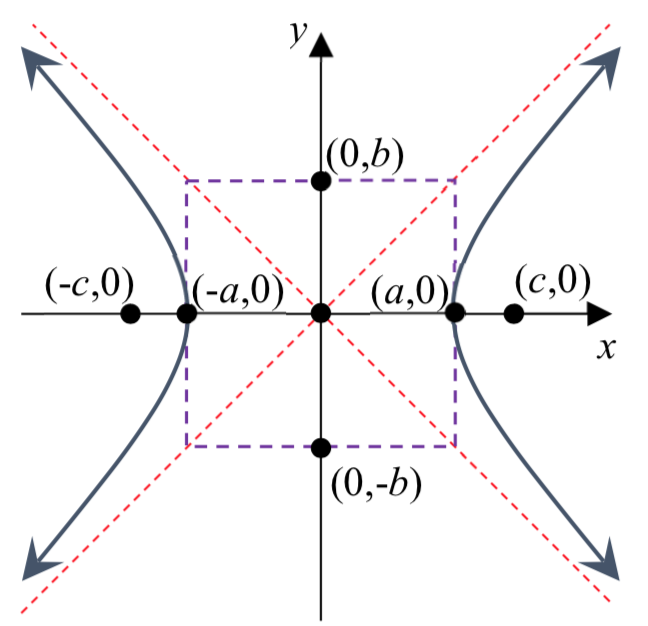 |
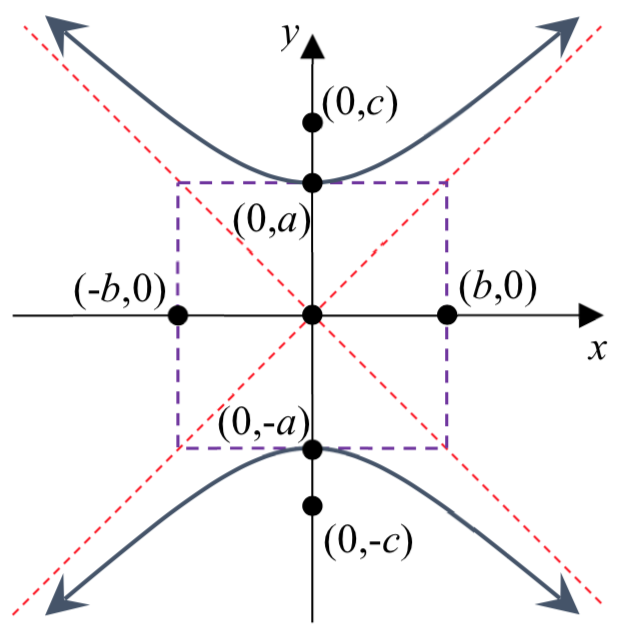 |
Ejemplo\(\PageIndex{1}\)
Poner la ecuación de la hipérbola\(y^2 - 4x^2 = 4\) en forma estándar. Encuentra los vértices, la longitud del eje transversal y las ecuaciones de las asíntotas. Esbozar la gráfica. Verifique usando una utilidad gráfica.
Solución
La ecuación se puede poner en forma estándar dividiendo\(\dfrac{y^2}{4} - \dfrac{x^2}{1} = 1\) por 4.
Comparando con la ecuación estándar general\(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\) vemos que\(a = \sqrt 4 = 2\) y\(b = \sqrt 1 = 1\).
Dado que se resta el\(x\) término, la hipérbola se abre verticalmente y los vértices se encuentran en el\(y\) eje -en (0,\(\pm a\)) = (0,\(\pm\) 2).
La longitud del eje transversal es\[2\left( a \right) = 2\left( 2 \right) = 4\nonumber\]
Las ecuaciones de las asíntotas son\[y = \pm \dfrac{a}{b}x\text{ or } = \pm 2x\nonumber\]
Para bosquejar la gráfica trazamos los vértices del rectángulo de construcción en\((\pm b, \pm a)\) o (-1, -2), (-1,2), (1, -2) y (1,2). Las asíntotas se dibujan a través de las diagonales del rectángulo y se trazan los vértices. Después dibujamos en la hipérbola, redondeados en los vértices y acercándonos a las asíntotas.
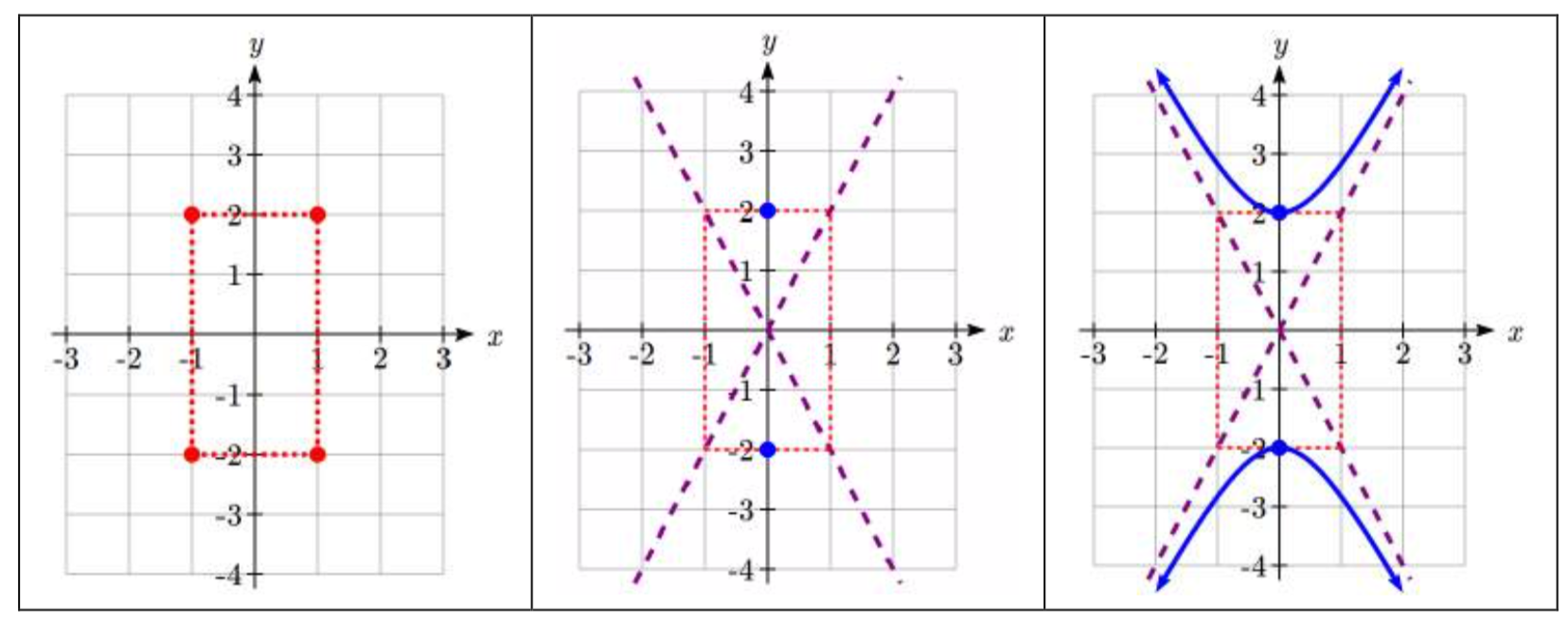
Para verificar una utilidad gráfica, debemos resolver la ecuación para\(y\). Aislar nos\(y^2\) da\(y^2 = 4\left( 1 + x^2 \right)\).
Tomando la raíz cuadrada de ambos lados nos encontramos\[y = \pm 2\sqrt {1 + x^2} \nonumber\]
Bajo Y= ingresan las dos mitades de la hipérbola y las dos asíntotas como\(y = 2\sqrt {1 + x^2} \),\(y = - 2\sqrt {1 + x^2} \),\(y = 2x\), y\(y = - 2x\). Establezca la ventana a una escala comparable al boceto con xmin = -4, xmax = 4, ymin= -3 e ymax = 3.

A veces se nos da la ecuación. A veces necesitamos encontrar la ecuación a partir de una gráfica u otra información.
Ejemplo\(\PageIndex{2}\)
Encuentra la forma estándar de la ecuación para una hipérbola con vértices en (-6,0) y (6,0) y asíntota\(y = \dfrac{4}{3}x\).
Solución
Dado que los vértices se encuentran en el\(x\) eje -con un punto medio en el origen, la hipérbola es horizontal con una ecuación de la forma\(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\). El valor de a es la distancia desde el centro hasta un vértice. La distancia de (6, 0) a (0, 0) es 6, entonces\(a\) = 6.
Las asíntotas siguen la forma\(y = \pm \dfrac{b}{a}x\). A partir de\(y = \dfrac{3}{4}x\) lo que vemos\(\dfrac{3}{4} = \dfrac{b}{a}\) y sustituyendo nos\(a = 6\) dan\(\dfrac{3}{4} = \dfrac{b}{6}\). Resolviendo rendimientos\(b = 8\).
La ecuación de la hipérbola en forma estándar es\[\dfrac{x^2}{6^2} - \dfrac{y^2}{8^2} = 1\text{ or }\dfrac{x^2}{36} - \dfrac{y^2}{64} = 1\nonumber\]
Ejercicio\(\PageIndex{2}\)
Encuentra la forma estándar de la ecuación para una hipérbola con vértices en (0, -8) y (0, 8) y asíntota\(y = 2x\)
- Contestar
-
Los vértices están en el\(y\) eje por lo que esta es una hipérbola vertical.
El centro está en el origen.
\[a = 8\nonumber\]Usando la pendiente asíntota,\(\dfrac{8}{b} = 2\), entonces\(b = 4\).
\[\dfrac{y^2}{64} - \dfrac{x^2}{16} = 1\nonumber\]
Ejemplo\(\PageIndex{3}\)
Encuentra la forma estándar de la ecuación para una hipérbola con vértices en (0, 9) y (0, -9) y pasando por el punto (8, 15).
Solución
Dado que los vértices se encuentran en el\(y\) eje -con un punto medio en el origen, la hipérbola es vertical con una ecuación de la forma\(\dfrac{y^2}{a^2} - \dfrac{x^2}{b^2} = 1\). El valor de a es la distancia desde el centro hasta un vértice. La distancia de (0, 9) a (0, 0) es 9, entonces\(a = 9\).
Sustituyendo\(a = 9\) y el punto (8, 15) da\(\dfrac{15^2}{9^2} - \dfrac{8^2}{b^2} = 1\). Resolviendo\(b\) rendimientos
\[b = \sqrt {\dfrac{9^2 \left( 8^2 \right)}{15^2 - 9^2}} = 6\nonumber\]
La ecuación estándar para la hipérbola es\[\dfrac{y^2}{9^2} - \dfrac{x^2}{6^2} = 1\text{ or}\dfrac{y^2}{81} - \dfrac{x^2}{36} = 1\nonumber\]
Hipérbolas no centradas en el origen
No todas las hipérbolas están centradas en el origen. La ecuación estándar para uno centrado en (\(h\),\(k\)) es ligeramente diferente.
EN FORMA ESTÁNDAR
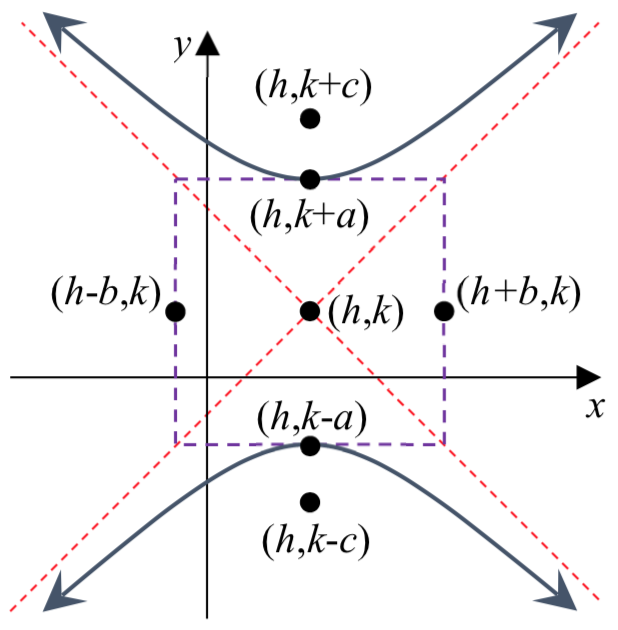
La forma estándar de una ecuación de una hipérbola centrada en\(C\left( h,k \right)\) depende de si se abre horizontal o verticalmente. La siguiente tabla da la ecuación estándar, vértices, focos, asíntotas, vértices de rectángulo de construcción y gráfica para cada uno.
| Abre | Horizontalmente | Verticalmente |
| Ecuación estándar | \(\dfrac{(x - h)^2}{a^2} - \dfrac{(y - k)^2}{b^2} = 1\) | \(\dfrac{(y - k)^2}{a^2} - \dfrac{(x - h)^2}{b^2} = 1\) |
| Vértices | \((h \pm a, k)\) | \((h, k \pm a)\) |
| Focos | \((h \pm c, k)\) donde\(b^2 = c^2 - a^2\) |
\((h, k \pm c)\) donde\(b^2 = c^2 - a^2\) |
| Asíntotas | \(y - k = \pm \dfrac{b}{a} (x - h)\) | \(y - k = \pm \dfrac{a}{b} (x - h)\) |
| Construcción Rectángulo Vértices | \((h \pm a, k \pm b)\) | \((h \pm b, k \pm a)\) |
| Gráfica | 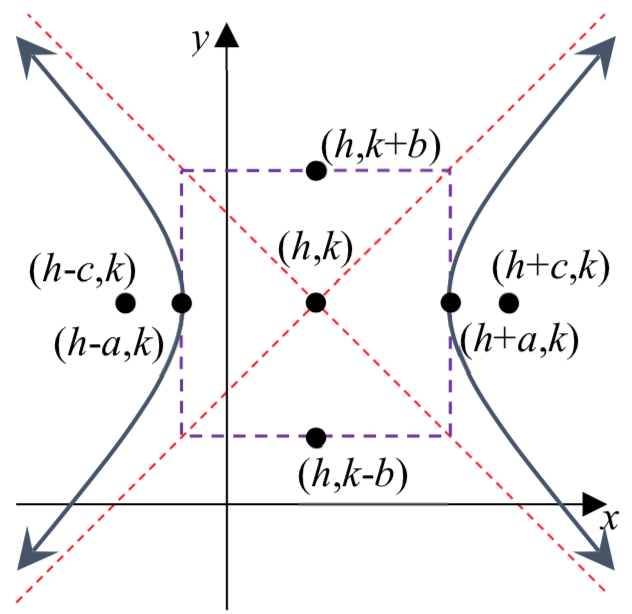 |
 |
Ejemplo\(\PageIndex{4}\)
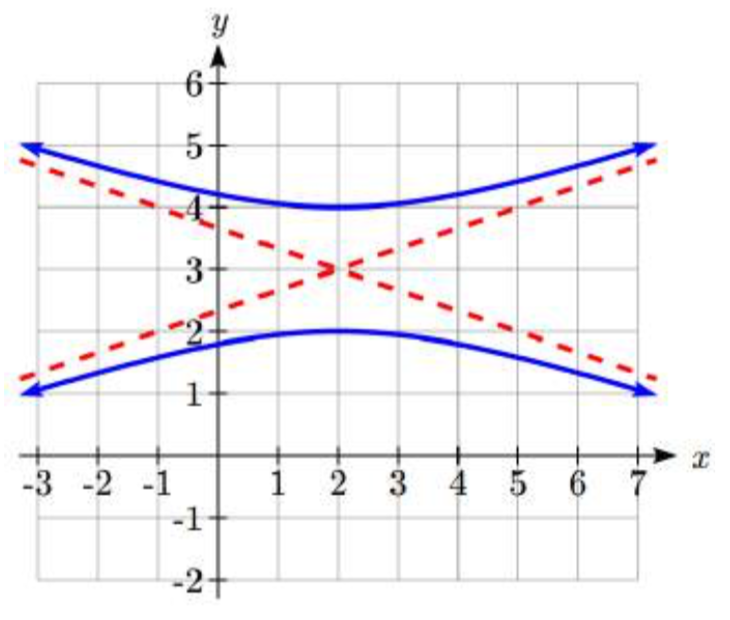
Escribe una ecuación para la hipérbola en la gráfica que se muestra.
Solución
El centro está en (2, 3), donde se cruzan las asíntotas. Se abre verticalmente, por lo que la ecuación se verá así\(\dfrac{\left( y - 3 \right)^2}{a^2} - \dfrac{\left( x - 2 \right)^2}{b^2} = 1\).
Los vértices están en (2, 2) y (2, 4). La distancia desde el centro a un vértice es\(a = 4 - 3 = 1\).
Si tuviéramos que dibujar en el rectángulo de construcción, se extendería de\(x = -1\) a\(x = 5\). La distancia desde el centro hasta el lado derecho del rectángulo da\(b = 5 - 2 = 3\).
La ecuación estándar de esta hipérbola es\[\dfrac{\left( y - 3 \right)^2}{1^2} - \dfrac{\left( x - 2 \right)^2}{3^2} = 1\text{, or }\left( y - 3 \right)^2 - \dfrac{\left( x - 2\right)^2}{9} = 1\nonumber\]
Ejemplo\(\PageIndex{5}\)
Poner la ecuación de la hipérbola\(9x^2 + 18x - 4y^2 + 16y = 43\) en forma estándar. Encuentra el centro, los vértices, la longitud del eje transversal y las ecuaciones de las asíntotas. Haga un boceto de la gráfica y, a continuación, compruebe una utilidad gráfica.
Solución
Para reescribir la ecuación, completamos el cuadrado para ambas variables para obtener
\(9\left( x^2 + 2x + 1 \right) - 4\left( y^2 - 4y + 4 \right) = 43 + 9 - 16\)
\(9\left( x + 1 \right)^2 - 4\left( y - 2 \right)^2 = 36\)
Dividir por 36 da la forma estándar de la ecuación,\[\dfrac{\left( x + 1 \right)^2}{4} - \dfrac{\left( y - 2 \right)^2}{9} = 1\nonumber\]
Comparando con la ecuación estándar general\(\dfrac{\left( x - h \right)^2}{a^2} - \dfrac{\left( h - k \right)^2}{b^2} = 1\) vemos que\[a = \sqrt 4 = 2\text{and }b = \sqrt 9 = 3\nonumber\]
Al restar el\(y\) término, la hipérbola se abre horizontalmente.
El centro está en (\(h\),\(k\)) = (-1, 2).
Los vértices están en (\(h \pm a\),\(k\)) o (-3, 2) y (1,2).
La longitud del eje transversal es\(2\left( a \right) = 2\left( 2 \right) = 4\).
Las ecuaciones de las asíntotas son\[y - k = \pm \dfrac{b}{a}\left( x - h \right)\text{ or }y - 2 = \pm \dfrac{3}{2}\left( x + 1 \right)\nonumber\]
Para bosquejar la gráfica trazamos las esquinas del rectángulo de construcción en (\(h \pm a\),\(k \pm b\)) o (1, 5), (1, -1), (-3, 5) y (-3, -1). Las asíntotas se dibujan a través de las diagonales del rectángulo y se trazan los vértices. Luego dibujamos en la hipérbola redondeada en los vértices y acercándonos a las asíntotas.
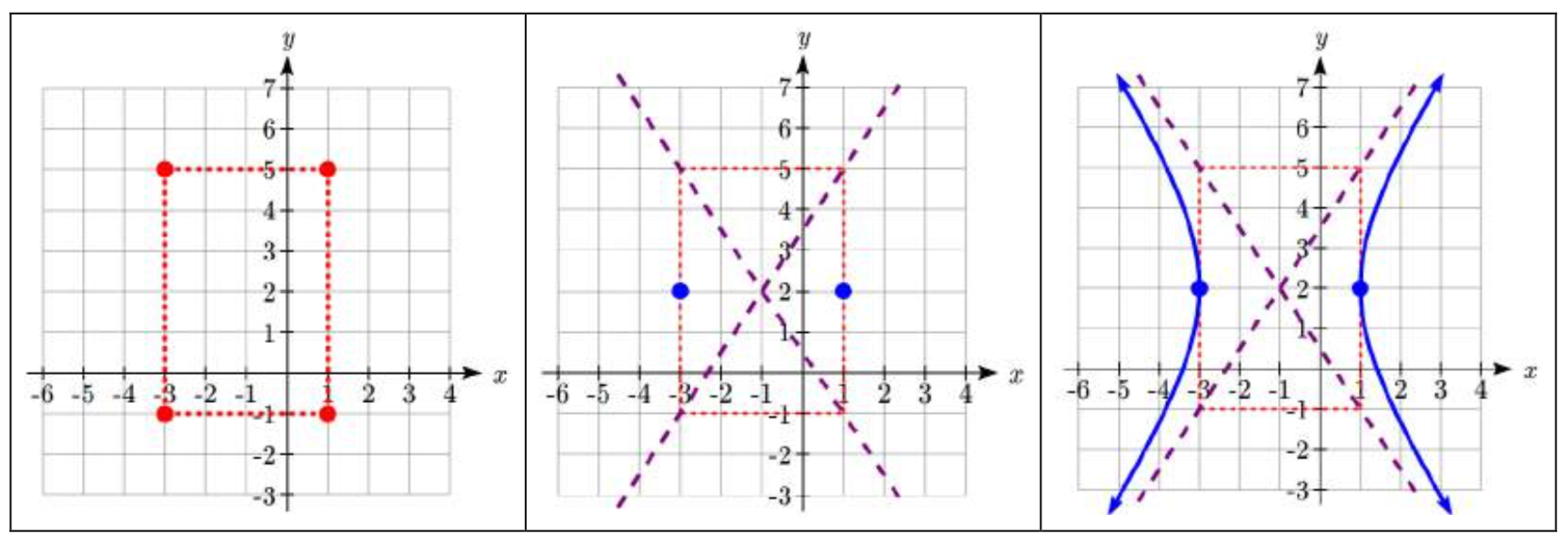
Para verificar una utilidad gráfica, debemos resolver la ecuación para\(y\).
\[y = 2 \pm \sqrt {9\left( \dfrac{\left( x + 1 \right)^2}{4} - 1 \right)} \nonumber\]
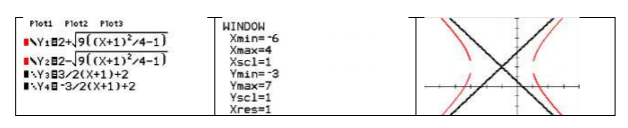
Bajo Y= ingrese las dos mitades de la hipérbola y las dos asíntotas como\[y = 2 + \sqrt {9\left( \dfrac{\left( x + 1 \right)^2}{4} - 1 \right)} \quad y = 2 - \sqrt {9\left( \dfrac{\left( x + 1 \right)^2}{4} - 1 \right)} \quad y = \dfrac{3}{2}\left( x + 1 \right) + 2\quad\text{, and }y = - \dfrac{3}{2}\left( x + 1 \right) + 2\nonumber\] Establecer la ventana a una escala comparable al boceto, luego graficar.
Tenga en cuenta que las brechas que ve en la calculadora no están realmente ahí; son una limitación de la tecnología.
Ejemplo\(\PageIndex{6}\)
Encuentra la forma estándar de la ecuación para una hipérbola con vértices en\(( - 2, - 5)\) y\(( - 2, 7)\), y asíntota\(y = \dfrac{3}{2}x + 4\).
Solución
Dado que los vértices difieren en las\(y\) coordenadas, la hipérbola se abre verticalmente con una ecuación de la forma\(\dfrac{\left( y - k \right)^2}{a^2} - \dfrac{\left( x - h\right)^2}{b^2} = 1\) y las ecuaciones de asíntota de la forma\[y - k = \pm \dfrac{a}{b}\left( x - h \right)\nonumber\]
El centro estará a medio camino entre los vértices, at\(\left( - 2,\dfrac{ - 5 + 7}{2} \right) = ( - 2,1)\).
El valor de a es la distancia desde el centro hasta un vértice. La distancia de\(( - 2,1)\) a\(( - 2, - 5)\) es de 6, entonces\(a = 6\).
Si bien nuestra asíntota no se da en la forma\(y - k = \pm \dfrac{a}{b}\left( {x - h} \right)\), observe que esta ecuación tendría pendiente\(\dfrac{a}{b}\). Podemos comparar eso con la pendiente de la ecuación de asíntota dada para encontrar b. El ajuste\(\dfrac{3}{2} = \dfrac{a}{b}\) y la sustitución nos\(a = 6\) da\(b = 4\).
La ecuación de la hipérbola en forma estándar es\[\dfrac{\left( y - 1 \right)^2}{6^2} - \dfrac{\left( x + 2 \right)^2}{4^2} = 1\text{ or }\dfrac{\left( y - 1 \right)^2}{36} - \dfrac{\left( x + 2 \right)^2}{16} = 1\nonumber\]
Ejercicio\(\PageIndex{2}\)
Encuentra el centro, vértices, longitud del eje transversal y ecuaciones de las asíntotas para la hipérbola\(\dfrac{\left( x + 5 \right)^2}{9} - \dfrac{\left( y - 2 \right)^2}{36} = 1\).
- Contestar
-
Centro (-5, 2). Se trata de una hipérbola horizontal. \(a = 3\). \(b = 6\).
longitud del eje transversal 6,
los vértices estarán en (-5\(\pm\) 3,2) = (-2, 2) y (-8, 2), la pendiente
asíntota será\(\dfrac{6}{3} = 2\). Asíntotas:\(y - 2 = \pm 2\left( x + 5 \right)\)
Focos de hipérbola
La ubicación de los focos puede jugar un papel clave en los problemas de aplicación de hipérbola. Para encontrarlos, necesitamos encontrar la longitud desde el centro hasta los focos,\(c\), usando la ecuación\(b^2 = c^2 - a^2\). Parece similar, pero no es lo mismo que, el Teorema de Pitágoras.
Compare esto con la ecuación para encontrar longitud\(c\) para elipses, que es\(b^2 = a^2 - c^2\). Si recuerdas que para que los focos estén dentro de la elipse tienen que venir antes que los vértices\((c < a)\), está claro por qué calcularíamos\(a^2\) menos\(c^2\). Para estar dentro de una hipérbola, los focos tienen que ir más allá de los vértices\((c > a)\), así podemos ver para las hipérbolas necesitamos\(c^2\) menos\(a^2\), lo contrario.
Ejemplo\(\PageIndex{7}\)
Encuentra los focos de la hipérbola\(\dfrac{\left( y + 1 \right)^2}{4} - \dfrac{\left( x - 3 \right)^2}{5} = 1\).
Solución
La hipérbola es vertical con una ecuación de la forma\[\dfrac{\left( y - k \right)^2}{a^2} - \dfrac{\left( x - h \right)^2}{b^2} = 1\nonumber\]
El centro está en (\(h\),\(k\)) = (3, -1). Los focos están en (\(h\),\(k \pm c\)).
Para encontrar la longitud c utilizamos\(b^2 = c^2 - a^2\). Sustitución da\[5 = c^2 - 4\text{ or }c = \sqrt 9 = 3\nonumber\]
La hipérbola tiene focos (3, -4) y (3, 2).
Ejemplo\(\PageIndex{8}\)
Encuentra la forma estándar de la ecuación para una hipérbola con focos (5, -8) y (-3, -8) y vértices (4, -8) y (-2, -8).
Solución
Dado que los vértices difieren en las\(x\) coordenadas, la hipérbola se abre horizontalmente con una ecuación de la forma\(\dfrac{\left( x - h \right)^2}{a^2} - \dfrac{\left( y - k \right)^2}{b^2} = 1\).
El centro está en el punto medio de los vértices\[\left( \dfrac{x_1 + x_2}{2},\dfrac{y_1 + y_2}{2} \right) = \left( \dfrac{4 + \left( - 2 \right)}{2},\dfrac{ - 8 + \left( - 8 \right)}{2} \right) = \left( 1, - 8 \right)\nonumber\]
El valor de\(a\) es la longitud horizontal desde el centro hasta un vértice, o\[a = 4 - 1 = 3\nonumber\]
El valor de\(c\) es la longitud horizontal desde el centro hasta un foco, o\[= 5 - 1 = 4\nonumber\]
Para encontrar la longitud\(b\) usamos\(b^2 = c^2 - a^2\). Sustituyendo da\[b^2 = 16 - 9 = 7\nonumber\]
La ecuación de la hipérbola en forma estándar es\[\dfrac{\left( x - 1 \right)^2}{3^2} - \dfrac{\left( y - \left( - 8 \right) \right)^2}{7} = 1\text{ or }\dfrac{\left( x - 1\right)^2}{9} - \dfrac{\left( y + 8\right)^2}{7} = 1\nonumber\]
Ejercicio\(\PageIndex{3}\)
Encuentra la forma estándar de la ecuación para una hipérbola con foco (1, 9), vértice (1, 8), centro (1, 4).
- Contestar
-
El foco, el vértice y el centro tienen el mismo\(x\) valor por lo que esta es una hipérbola vertical.
Usando el vértice y el centro,\[a = 9 – 4 = 5\nonumber\]
Usando el foco y el centro,\[c = 8 – 4 = 4\nonumber\]
\[b^2 =5^2 - 4^2\quad b = 3\nonumber\]
\[\dfrac{\left( y - 4 \right)^2}{16} - \dfrac{\left( x - 1 \right)^2}{9} = 1\nonumber\]
LORAN 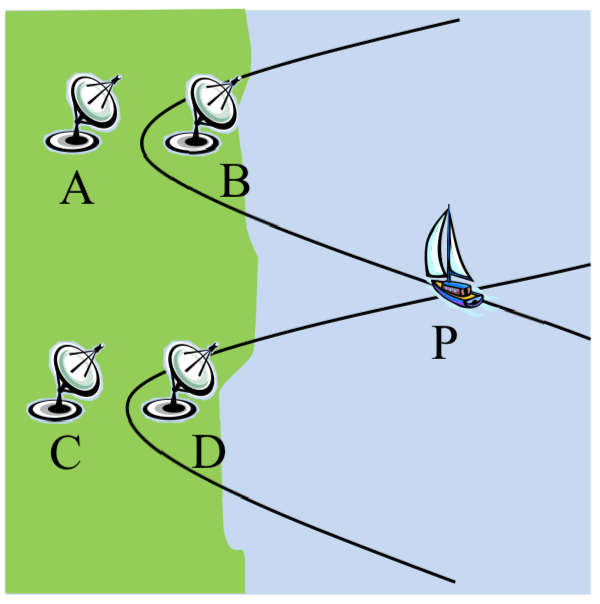
Antes del GPS, se utilizó el sistema de Navegación de Largo Alcance (LORAN) para determinar la ubicación de un barco. Dos estaciones de radio A y B enviaron simultáneamente una señal a un barco. La diferencia de tiempo que tardó en recibir la señal se computó como una distancia ubicando el barco en la hipérbola con las estaciones de radio A y B como focos. Un segundo par de estaciones de radio C y D enviaron señales simultáneas a la nave y computaron su ubicación en la hipérbola con C y D como focos. El punto P donde se cruzaron las dos hipérbolas dio la ubicación de la nave.
Ejemplo\(\PageIndex{9}\)
Las estaciones A y B están a 150 kilómetros de distancia y envían una señal de radio simultánea al barco. La señal de B llega 0.0003 segundos antes de la señal de A. Si la señal recorre 300,000 kilómetros por segundo, encuentra la ecuación de la hipérbola sobre la que se posiciona la nave.
Solución
Las estaciones A y B están en los focos, por lo que la distancia desde el centro a un foco es la mitad de la distancia entre ellas, dando\(c = \dfrac{1}{2}(150) = 75\) km.
Al dejar que el centro de la hipérbola esté en (0, 0) y colocando los focos en (\(\pm\)75,0), se puede utilizar la ecuación\(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\) para una hipérbola centrada en el origen.
La diferencia de las distancias del barco desde las dos estaciones es\(k = 300,000\dfrac{\rm{km}}{\rm{s}} \cdot (0.0003 \rm{s}) = 90 \rm{km}\). A partir de nuestra derivación de la ecuación de la hipérbola determinamos\(k = 2a\), así\[a = \dfrac{1}{2}(90) = 45\nonumber\]
Sustitución\(a\) y\(c\) en\(b^2 = c^2 - a^2\) rendimientos\[b^2 = 75^2 - 45^2 = 3600\nonumber\]
La ecuación de la hipérbola en forma estándar es\[\dfrac{x^2}{45^2} - \dfrac{y^2}{3600} = 1\text{ or }\dfrac{x^2}{2025} - \dfrac{y^2}{3600} = 1\nonumber\]
Para determinar la posición de una nave usando LORAN, necesitaríamos una ecuación para la segunda hipérbola y resolveríamos para la intersección. Exploraremos cómo hacerlo en la siguiente sección.
Temas Importantes de esta Sección
- Definición de hipérbola
- Ecuaciones de hipérbola en forma estándar
- Focos de hipérbola
- Aplicaciones de Hyperbolas
- Intersecciones de hipérbolas y otras curvas


