9.1: Elipses

Última actualización
Guardar como PDF

Page ID: 116768

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El Salón Nacional de Estatuas en Washington, D.C. es una sala de forma ovalada llamada cámara susurrante porque la forma permite que el sonido se refleje desde las paredes de una manera especial. Dos personas paradas en lugares específicos son capaces de escucharse susurrar a pesar de que están muy separadas. Para determinar dónde deben estar, necesitaremos comprender mejor las elipses.

$image1.jpeg$

Foto de Gary Palmer, Flickr, CC-BY, https://www.flickr.com/photos/gregpalmer/2157517950

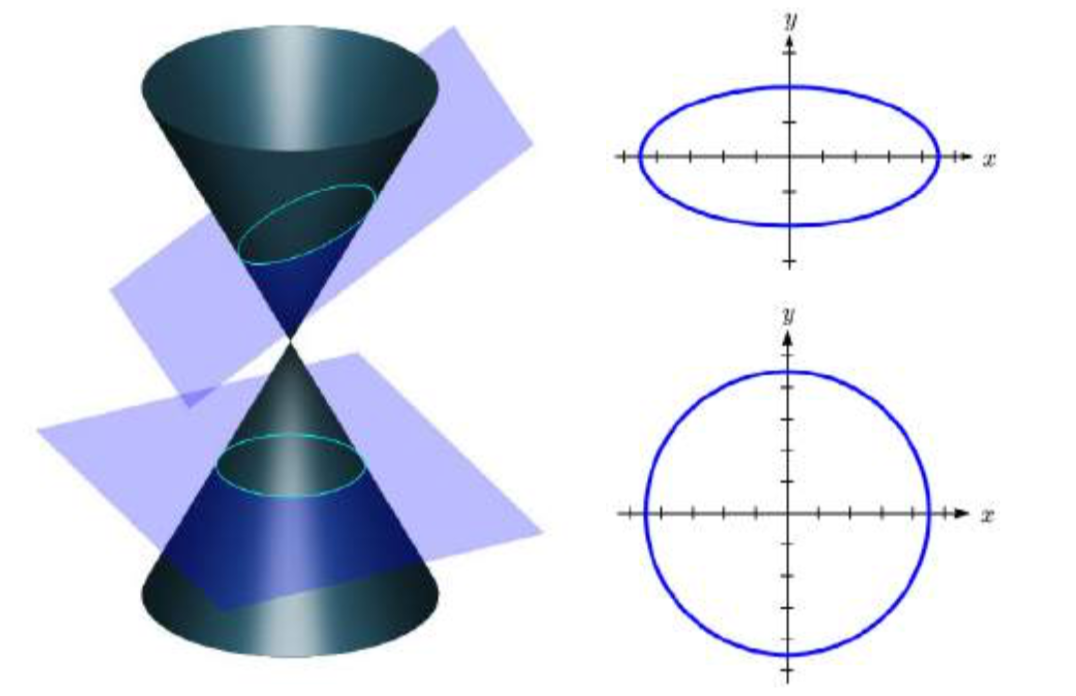
Una elipse es un tipo de sección cónica, una forma resultante de intersectar un plano con un cono y mirar la curva donde se cruzan. Fueron descubiertos por el matemático griego Menaechmus hace más de dos milenios.

La siguiente figura (Pbroks13 (Commons.wikimedia.org/wiki/F... with_plane.svg), “Secciones cónicas con plano”, recortadas para mostrar solo elipse y círculo por L Michaels, CC BY 3.0) muestra dos tipos de secciones cónicas. Cuando un plano es perpendicular al eje del cono, la forma de la intersección es un círculo. Un plano ligeramente titulado crea una sección cónica de forma ovalada llamada elipse.

$2019-07-25 5.17.14.png$

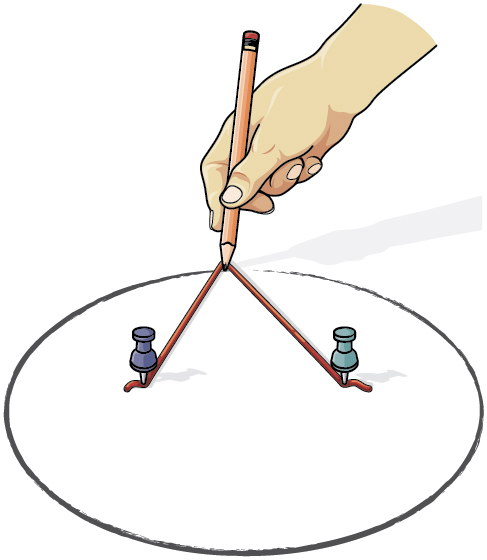
Se puede dibujar una elipse colocando dos tachuelas en un trozo de cartón y luego cortando un trozo de cuerda más largo que la distancia entre las tachuelas. Pegue cada extremo de la cuerda al cartón, y trace una curva con un lápiz sostenido enseñado contra la cuerda. Una elipse es el conjunto de todos los puntos donde la suma de las distancias desde dos puntos fijos es constante. La longitud de la cadena es la constante, y las dos chinchetas son los puntos fijos, llamados focos.

$image5.png$

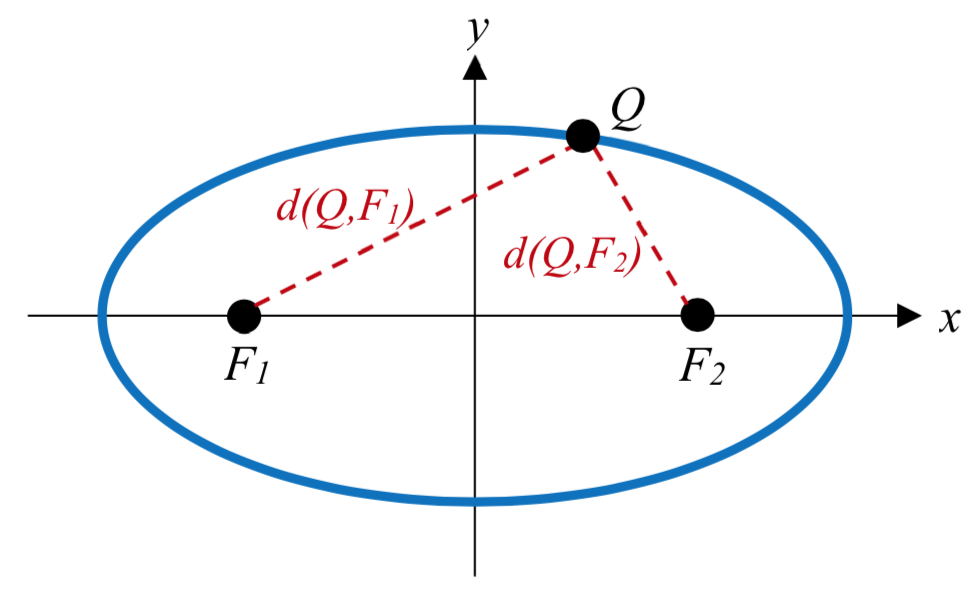
Definición: ELIPSE Definición Y Vocabulario

Una elipse es el conjunto de todos los puntos$\;Q\left( {x,y} \right)$ para los cuales la suma de la distancia a dos puntos fijos$F_1 \left( x_1,y_1 \right)$ y$F_2 \left( x_2,y_2 \right)$, llamados los focos (plural de foco), es una constante k:\[d\left( {Q,{F_1}} \right) + d\left( {Q,{F_2}} \right) = k\]

$2019-07-25 5.18.15.png$

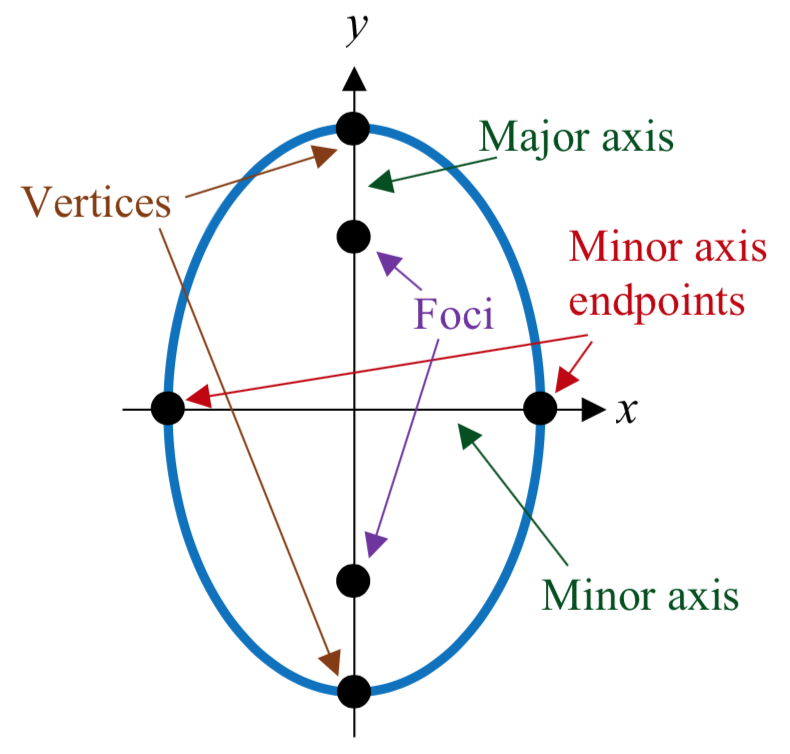
El eje mayor es la línea que pasa por los focos.
Los vértices son los puntos en la elipse que se cruzan con el eje mayor.
La longitud del eje mayor es la longitud del segmento de línea entre los vértices.
El centro es el punto medio entre los vértices (o el punto medio entre los focos).
El eje menor es la línea perpendicular al eje menor que pasa por el centro.
Los puntos finales del eje menor son los puntos de la elipse que se cruzan con el eje menor.
Los puntos finales del eje menor también se denominan a veces co-vértices.
La longitud del eje menor es la longitud del segmento de línea entre los extremos del eje menor.

Tenga en cuenta que qué eje es mayor y cuál es menor dependerá de la orientación de la elipse. En la elipse que se muestra a la derecha, los focos se encuentran sobre el$y$ eje, de manera que ese es el eje mayor, y el$x$ eje es el eje menor. Debido a esto, los vértices son los puntos finales de la elipse en el$y$ eje, y los puntos finales del eje menor (co-vértices) son los puntos finales en el$x$ eje.

$2019-07-25 5.19.51.png$

Elipses Centradas en el Origen

De la definición anterior podemos encontrar una ecuación para una elipse. Lo encontraremos por una elipse centrada en el origen$C\left( {0,0} \right)$ con focos en${F_1}\left( {c,0} \right)$ y${F_2}\left( { - c,0} \right)$ dónde$c > 0$.

Supongamos que$\;Q\left( {x,y} \right)$ hay algún punto en la elipse. La distancia de$F_1$ a$Q$ es

\[d\left( Q,{F_1} \right) = \sqrt {{{\left( {x - c} \right)}^2} + {{\left( {y - 0} \right)}^2}\;} = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}\;} \nonumber\]

Así mismo, la distancia de$F_2$ a$Q$ es

\[d\left( {Q,{F_2}} \right) = \sqrt {{\left( {x - \left( { - c} \right)} \right)}^2 + {\left( {y - 0} \right)}^2} = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}\;} \nonumber\]

A partir de la definición de elipse, la suma de estas distancias debe ser constante:

\[d\left( {Q,{F_1}} \right) + d\left( {Q,{F_2}} \right) = k\nonumber\]para que
\[\sqrt {\left( {x - c} \right)^2} + y^2; + \sqrt {{{\left( {x + c} \right)}^2} + {y^2}\;} = k\nonumber\]

Si etiquetamos uno de los vértices$\left( a,0 \right)$, debería satisfacer la ecuación anterior ya que es un punto en la elipse. Esto nos permite escribir$k$ en términos de$a$.

\[\sqrt {\left( a - c \right)^2 +0^2} + \sqrt {\left( a + c \right)^2 + 0^2} = k\nonumber\]
\[\left| {a - c} \right| + \left| {a + c} \right| = k\nonumber\]Ya que$a > c$, estos serán positivos
\[(a - c) + (a + c) = k\nonumber\]
\[2a = k\nonumber\]

Sustituyendo eso en nuestra ecuación, ahora intentaremos reescribir la ecuación de una forma más amigable.

\[\sqrt {\left( x - c \right)^2 + y^2} + \sqrt {\left( x + c \right)^2 + y^2} = 2a\nonumber\]Mover un radical
\[\sqrt {\left( x - c \right)^2 + y^2} = 2a - \sqrt {\left( x + c \right)^2 + y^2} \nonumber\] Cuadrar ambos lados
\[\left( \sqrt {\left( x - c \right)^2 + y^2 } \right)^2 = \left( 2a - \sqrt {\left( x + c \right)^2 + y^2} \right)^2\nonumber\] Ampliar
\[\left( x - c \right)^2 + y^2= 4a^2 - 4a\sqrt {\left( x + c \right)^2 + y^2} + \left( x + c \right)^2 + y^2\nonumber\] Ampliar más
\[x^2 - 2xc + c^2 + y^2 = 4a^2 - 4a\sqrt {\left( x + c \right)^2 + y^2} + x^2 + 2xc + c^2 + y^2\nonumber\]

Combinando términos similares y aislando las hojas radicales

\[4a\sqrt {\left( x + c \right)^2 + y^2} = 4a^2 + 4xc\nonumber\]Dividir por 4
\[a\sqrt {\left( x + c \right)^2 + y^2} = a^2 + xc\nonumber\] Cuadrar ambos lados otra vez
\[a^2\left( \left( x + c \right)^2 + y^2 \right) = a^4 + 2a^2xc + x^2c^2\nonumber\] Ampliar
\[a^2\left( x^2 + 2xc + c^2 + y^2 \right) = a^4 + 2a^2xc + x^2c^2\nonumber\] Distribuir
\[a^2x^2 + 2a^2xc + a^2c^2 + a^2y^2 = a^4 + 2a^2xc + x^2c^2\nonumber\] Combinar términos similares
\[a^2x^2 - x^2c^2 + a^2y^2 =a^4 - a^2c^2\nonumber\] Factor términos comunes
\[\left( a^2 - c^2 \right)x^2 + a^2y^2 = a^2\left( a^2 - c^2 \right)\nonumber\]

Vamos$b^2 = a^2 - c^2$. Ya que$a > c$, sabemos$b > 0$. Sustitución$b^2$ de$a^2 - c^2$ hojas

\[b^2x^2 + a^2y^2 = a^2b^2\nonumber\]Divide ambos lados por$a^2b^2$
\[\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\nonumber\]

Esta es la ecuación estándar para una elipse. Normalmente intercambiamos$a$ y$b$ cuando el eje mayor de la elipse es vertical.

Definición: ECUACIÓN DE UNA ELIPSE CENTRADA AL ORIGEN EN FORMA ESTÁNDAR

La forma estándar de una ecuación de una elipse centrada en el origen$C\left( 0,0 \right)$ depende de si el eje mayor es horizontal o vertical. La siguiente tabla da la ecuación estándar, los vértices, los puntos finales del eje menor, los focos y la gráfica para cada uno.

Eje Mayor	Horizontal	Vertical
Vértices	$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$	$\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1$
Ecuación estándar	(-$a$, 0) y ($a$, 0)	(0, -$a$) y (0,$a$)
Puntos finales del eje menor	(0, -$b$) y (0,$b$)	(-$b$, 0) y ($b$, 0)
Focos	(-$c$, 0) y ($c$, 0) donde$b^2 = a^2 - c^2$	(0, -$c$) y (0,$c$) donde$b^2 = a^2 - c^2$
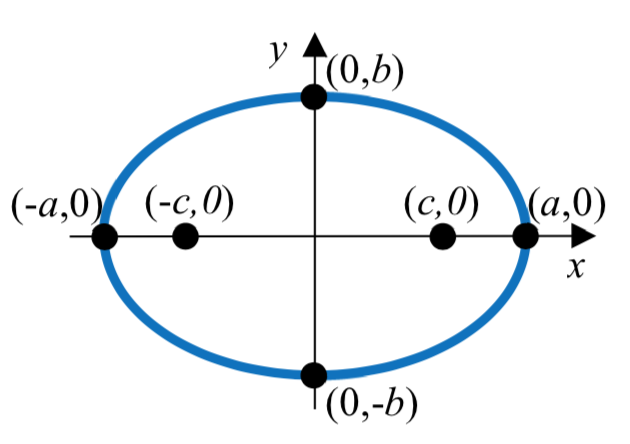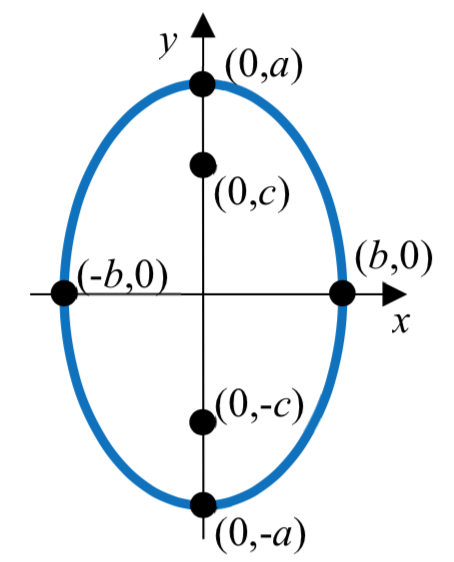Gráfica	$2019-07-25 5.44.04.png$	$2019-07-25 5.44.22.png$

Ejemplo$\PageIndex{1}$

Poner la ecuación de la elipse$9{x^2} + {y^2} = 9$ en forma estándar. Encuentra los vértices, los extremos del eje menor, la longitud del eje mayor y la longitud del eje menor. Haga un boceto de la gráfica y, a continuación, verifique con una utilidad gráfica.

Solución

La ecuación estándar tiene un 1 en el lado derecho, por lo que esta ecuación se puede poner en forma estándar dividiendo por 9:

\[\dfrac{x^2}{1} + \dfrac{y^2}{9} = 1\nonumber\]

Dado que el$y$ -denominador es mayor que el$x$ -denominador, la elipse tiene un eje mayor vertical. Comparando con la ecuación general de forma estándar$\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1$, vemos el valor de$a = \sqrt 9 = 3$ y el valor de$b = \sqrt 1 = 1$.

Los vértices se encuentran en el$y$ eje -en (0,$\pm a$) = (0,$\pm 3$).
Los extremos del eje menor se encuentran en el$x$ eje -en ($\pm b$, 0) = ($\pm 1$, 0).
La longitud del eje mayor es$2\left( a \right) = 2\left( 3 \right) = 6$.
La longitud del eje menor es$2\left( b \right) = 2\left( 1 \right) = 2$.

Para bosquejar la gráfica trazamos los vértices y los extremos del eje menor. Después esbozamos la elipse, redondeando en los vértices y los puntos finales del eje menor.

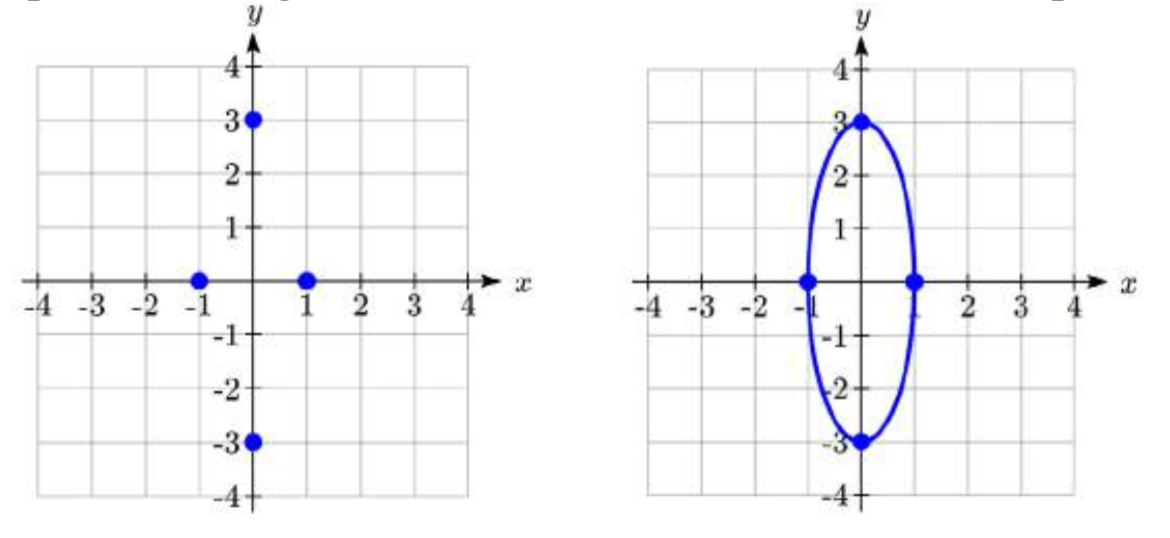
$2019-07-25 5.48.45.png$

Para verificar una utilidad gráfica, debemos resolver la ecuación para$y$. Aislar nos$y^2$ da

\[y^2 = 9\left( 1 - x^2 \right)\nonumber\]

Tomando la raíz cuadrada de ambos lados obtenemos

\[y = \pm 3\sqrt {1 - x^2} \nonumber\]

Bajo Y= en su utilidad gráfica ingrese las dos mitades de la elipse como$y = 3\sqrt {1 - x^2} $ y$y = - 3\sqrt {1 - x^2} $. Establezca la ventana a una escala comparable al boceto con xmin = -5, xmax = 5, ymin= -5 e ymax = 5.

Aquí hay un resultado de ejemplo en una calculadora TI-84:

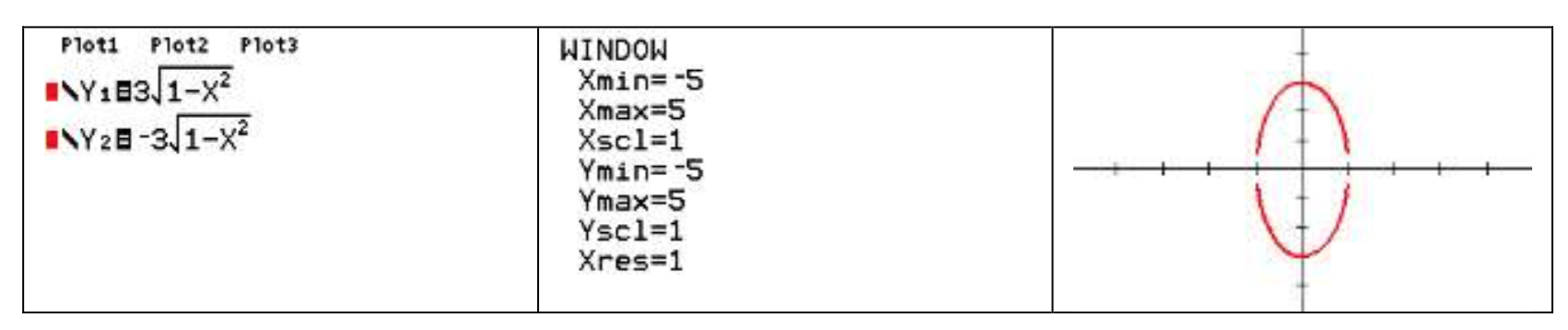
$2019-07-25 5.50.59.png$

A veces se nos da la ecuación. A veces necesitamos encontrar la ecuación a partir de una gráfica u otra información.

Ejemplo$\PageIndex{2}$

Encuentre la forma estándar de la ecuación para una elipse centrada en (0,0) con la longitud del eje mayor horizontal 28 y la longitud del eje menor 16.

Solución

Dado que el centro está en (0,0) y el eje mayor es horizontal, la ecuación de elipse tiene la forma estándar$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$. El eje mayor tiene longitud$2a = 28$ o$a = 14$. El eje menor tiene longitud$2b = 16$ o b = 8. Sustitución da\[\dfrac{x^2}{16^2} + \dfrac{y^2}{8^2} = 1\text{ or }\dfrac{x^2}{256} + \dfrac{y^2}{64.} = 1\nonumber\]

Ejercicio$\PageIndex{1}$

Encuentre la forma estándar de la ecuación para una elipse con longitud de eje mayor horizontal 20 y longitud de eje menor 6.

Contestar: $2a = 20$, entonces$a =10$. $2b = 6$, entonces$b = 3$. \[\dfrac{x^2}{100} + \dfrac{y^2}{9} = 1\nonumber\]

Ejemplo$\PageIndex{3}$

Encuentra la forma estándar de la ecuación para la elipse graficada aquí.

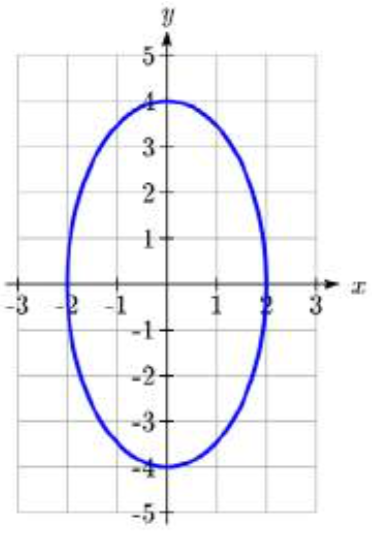
$2019-07-29 11.18.25.png$

Solución

El centro está en (0,0) y el eje mayor es vertical, por lo que la forma estándar de la ecuación será$\dfrac{x^2}{b^2} + \dfrac{y^2}{a^2} = 1$.

De la gráfica podemos ver que los vértices son (0,4) y (0, -4), dando$a = 4$.

Los extremos del eje menor son (2,0) y (-2,0), dando$b = 2$.

La ecuación será\[\dfrac{x^2}{2^2} + \dfrac{y^2}{4^2} = 1\text{ or }\dfrac{x^2}{4} + \dfrac{y^2}{16} = 1\nonumber\]

Elipses no Centradas en el Origen

No todas las elipses están centradas en el origen. La gráfica de tal elipse es un desplazamiento de la gráfica centrada en el origen, por lo que la ecuación estándar para una centrada en ($h$,$k$) es ligeramente diferente. Podemos cambiar las$h$ unidades correctas de la gráfica y subir$k$ unidades reemplazando$x$ con$x – h$ y$y$ con$y – k$, similar a lo que hicimos cuando aprendimos transformaciones.

Definición: Ecuación de una elipse centrada en$(h,k)$ IN STANDARD FORM

La forma estándar de una ecuación de una elipse centrada en el punto C$\left( {h,k} \right)$ depende de si el eje mayor es horizontal o vertical. La siguiente tabla da la ecuación estándar, los vértices, los puntos finales del eje menor, los focos y la gráfica para cada uno.

Eje Mayor	Horizontal	Vertical
Ecuación estándar	$\dfrac{(x - h)^2}{a^2} + \dfrac{(y - k)^2}{b^2} = 1$	$\dfrac{(x - h)^2}{b^2} + \dfrac{(y - k)^2}{a^2} = 1$
Vértices	$(h \pm a, k)$	$(h, k \pm a)$
Puntos finales del eje menor	$(h, k \pm b)$	$(h \pm b, k)$
Focos	$(h \pm c, k)$ donde$b^2 = a^2 - c^2$	$(h, k \pm c)$ donde$b^2 = a^2 - c^2$
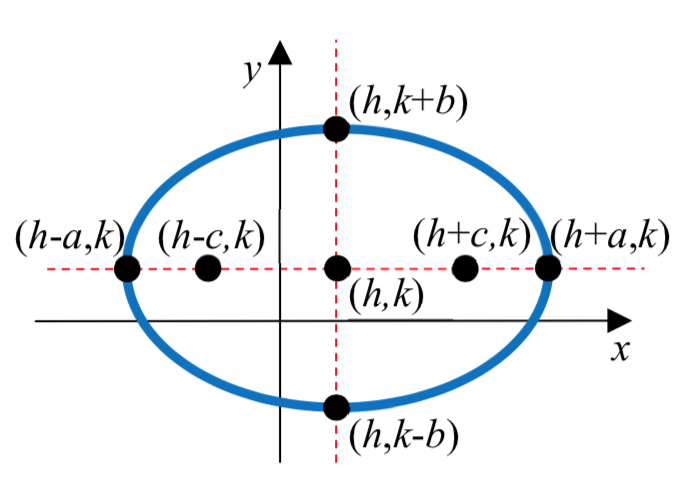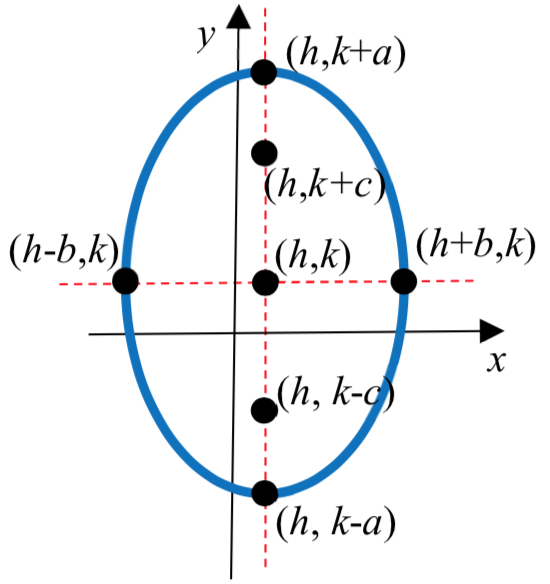Gráfica	$2019-07-29 11.25.18.png$	$2019-07-29 11.25.37.png$

Ejemplo$\PageIndex{4}$

Poner la ecuación de la elipse$x^2 + 2x + 4y^2 - 24y = - 33$ en forma estándar. Encuentra los vértices, los extremos del eje menor, la longitud del eje mayor y la longitud del eje menor. Esbozar la gráfica.

Solución

Para reescribir esto en forma estándar, necesitaremos completar el cuadrado, dos veces.

Mirando los$x$ términos,$x^2 + 2x$, nos gusta tener algo de la forma$(x + n)^2$. Observe que si tuviéramos que expandir esto, lo obtendríamos$x^2 + 2nx + n^2$, así que para que el coeficiente encendido$x$ coincida, necesitaremos$(x + 1)^2 = x^2 + 2x + 1$. Sin embargo, no tenemos$a +1$ en el lado izquierdo de la ecuación para permitir esta factorización. Para acomodar esto, agregaremos 1 a ambos lados de la ecuación, lo que luego nos permite factorizar el lado izquierdo como un cuadrado perfecto:

\[x^2 + 2x + 1 + 4y^2 - 24y = - 33 + 1\nonumber\]
\[(x + 1)^2 + 4y^2 - 24y = - 32\nonumber\]

Repitiendo el mismo enfoque con los$y$ términos, primero vamos a factorizar el 4.

\[4y^2 - 24y = 4(y^2 - 6y)\nonumber\]

Ahora queremos poder escribir$4\left( y^2 - 6y \right)$ como

\[4(y + n)^2 = 4\left( y^2 + 2ny + n^2 \right)\nonumber\]

Para que el coeficiente de$y$ igualar,$n$ tendrá que -3, dando$4(y - 3)^2 = 4\left( y^2 - 6y + 9 \right) = 4y^2 - 24y + 36$.

Para permitir esta factorización, podemos sumar 36 a ambos lados de la ecuación.

\[(x + 1)^2 + 4y^2 - 24y + 36 = - 32 + 36\nonumber\]
\[(x + 1)^2 + 4\left( y^2 - 6y + 9 \right) = 4\nonumber\]
\[(x + 1)^2 + 4\left( y - 3 \right)^2 = 4\nonumber\]

Dividir por 4 da la forma estándar de la ecuación para la elipse

\[\dfrac{\left( x + 1 \right)^2}{4} + \dfrac{\left( y - 3 \right)^2}{1} = 1\nonumber\]

Dado que el$x$ -denominador es mayor que el$y$ -denominador, la elipse tiene un eje mayor horizontal. A partir de la ecuación estándar general$\dfrac{\left( x - h \right)^2}{a^2} + \dfrac{\left( h - k \right)^2}{b^2} = 1$ vemos el valor de$a = \sqrt 4 = 2$ y el valor de$b = \sqrt 1 = 1$.

El centro está en ($h$,$k$) = (-1, 3).
Los vértices están en ($h \pm a$,$k$) o (-3, 3) y (1,3).
Los puntos finales del eje menor están en ($h$,$k \pm b$) o (-1, 2) y (-1,4).
La longitud del eje mayor es$2\left( a \right) = 2\left( 2 \right) = 4$.
La longitud del eje menor es$2\left( b \right) = 2\left( 1 \right) = 2$.

Para bosquejar la gráfica trazamos los vértices y los extremos del eje menor. Después esbozamos la elipse, redondeando en los vértices y los puntos finales del eje menor.

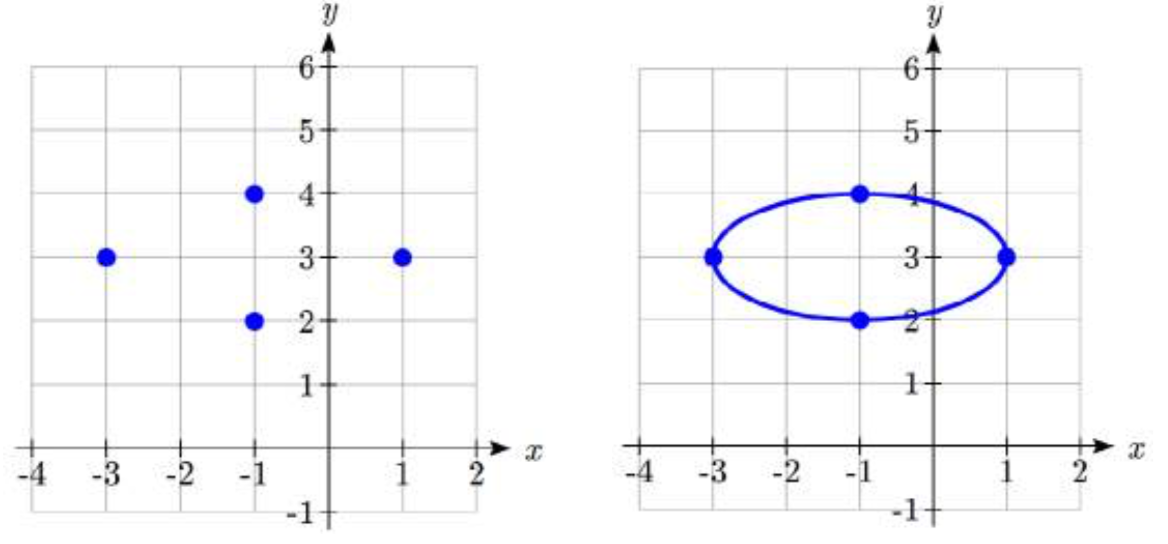
$2019-07-29 11.32.10.png$

Ejemplo$\PageIndex{5}$

Encuentra la forma estándar de la ecuación para una elipse centrada en (-2,1), un vértice en (-2,4) y pasando por el punto (0,1).

Solución

El centro en (-2,1) y el vértice en (-2,4) significan que el eje mayor es vertical ya que los valores x son los mismos. La ecuación de elipse tiene la forma estándar

\[\dfrac{\left( x - h \right)^2}{b^2} + \dfrac{\left( y - k \right)^2}{a^2} = 1\nonumber\]

El valor de$a = 4 - 1 = 3$. Sustituyendo$a = 3$,$h = -2$, y$k = 1$ da

\[\dfrac{\left( x + 2 \right)^2}{b^2} + \dfrac{\left( y - 1 \right)^2}{3^2} = 1\nonumber\]Sustituir$x$ y$y$ usar el punto (0,1) da

\[\dfrac{\left( 0 + 2 \right)^2}{b^2} + \dfrac{\left( 1 - 1 \right)^2}{3^2} = 1\nonumber\]
Resolviendo para b da$b = 2$.
La ecuación de la elipse en forma estándar es\[\dfrac{\left( x + 2 \right)^2}{2^2} + \dfrac{\left( y - 1 \right)^2}{3^2} = 1\text{ or }\dfrac{\left( x + 2 \right)^2}{4} + \dfrac{\left( y - 1 \right)^2}{9} = 1\nonumber\]

Ejercicio$\PageIndex{2}$

Encuentra el centro, los vértices, los extremos del eje menor, la longitud del eje mayor y la longitud del eje menor para la elipse$\left( x - 4 \right)^2 + \dfrac{\left( y + 2 \right)^2}{4} = 1$.

Contestar: Centro (4, -2). Elipse vertical con$a = 2$,$b = 1$.
Vértices en (4, -2$\pm$ 2) = (4, 0) y (4, -4), extremos del eje
menor en (4$\pm$ 1, -2) = (3, -2) y (5, -2), longitud del eje
mayor 4, longitud del eje menor 2

Puentes con Arcos Semielípticos

Los arcos se han utilizado para construir puentes durante siglos, como en el Puente Skerton en Inglaterra que utiliza cinco arcos semielípticos como soporte. Los arcos semielípticos pueden tener beneficios de ingeniería, como permitir tramos más largos entre soportes.

$2019-07-29 11.37.19.png$

(Maxine Armstrong (Commons.wikimedia.org/wiki/F... r, _England.JPG), “Puente de Skerton, Lancaster, Inglaterra”, CC BY-SA)

Ejemplo$\PageIndex{6}$

Un puente sobre un río está sostenido por un solo arco semielíptico. El río tiene 50 pies de ancho. En el centro, el arco se eleva a 20 pies sobre el río. La calzada está a 4 pies por encima del centro del arco. ¿Cuál es la distancia vertical entre la calzada y el arco a 15 pies del centro?

Solución

Poner el centro de la elipse en (0,0) y hacer que la envergadura del río sea el eje mayor.

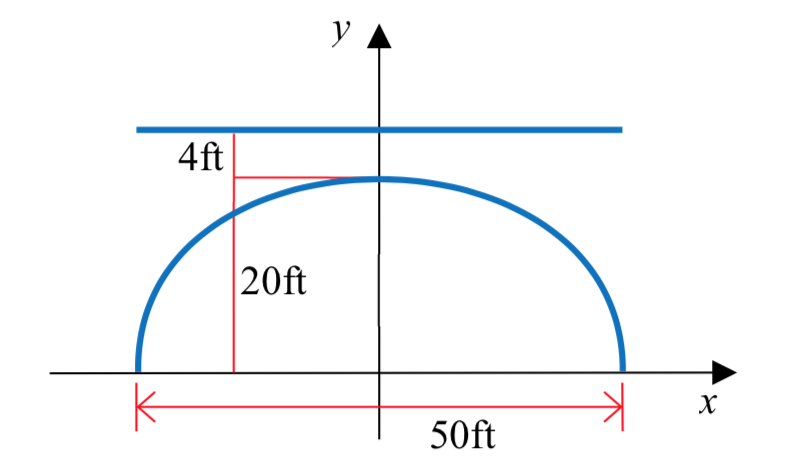
$2019-07-29 11.39.24.png$

Dado que el eje mayor es horizontal, la ecuación tiene la forma$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$.

El valor de$a = \dfrac{1}{2}(50) = 25$ y el valor de$b = 20$, dar$\dfrac{x^2}{25^2} + \dfrac{y^2}{15^2} = 1$.

Sustituyendo$x = 15$ da$\dfrac{15^2}{25^2} + \dfrac{y^2}{20^2} = 1$. Resolviendo para$y$,\[y = 20\sqrt {1 - \dfrac{225}{625}} = 16\nonumber\]

La calzada se encuentra a 20 + 4 = 24 pies sobre el río. La distancia vertical entre la calzada y el arco a 15 pies del centro es de 24 - 16 = 8 pies.

Focos de elipse

La ubicación de los focos puede jugar un papel clave en los problemas de aplicación de elipse. Pararse en un foco en una galería susurrante te permite escuchar a alguien susurrando al otro enfoque. Para encontrar los focos, necesitamos encontrar la longitud desde el centro hasta los focos,$c$, usando la ecuación${b^2} = {a^2} - {c^2}$. Parece similar, pero no es lo mismo que, el Teorema de Pitágoras.

Ejemplo$\PageIndex{7}$

La cámara susurrante del Salón Nacional de Estatuas es una sala elíptica de 46 pies de ancho y 96 pies de largo. Para escucharse susurrar, dos personas necesitan pararse ante los focos de la elipse. ¿Dónde deberían pararse?

Solución

Podríamos representar la sala con una elipse horizontal centrada en el origen. La longitud del eje mayor sería de 96 pies, así$a = \dfrac{1}{2}(96) = 48$, y la longitud del eje menor sería de 46 pies, entonces$b = \dfrac{1}{2}(46) = 23$. Para encontrar los focos, podemos usar la ecuación$b^2 = a^2 - c^2$.

\[23^2 =48^2 - c^2\nonumber\]
\[c^2 = 48^2 - 23^2\nonumber\]
\[c = \sqrt {1775} \approx \pm 42\text{ ft}\nonumber\]

Para escucharse susurrar, dos personas necesitarían pararse 2 (42) = 84 pies de distancia a lo largo del eje mayor, cada una a unos 48 — 42 = 6 pies de la pared.

Ejemplo$\PageIndex{8}$

Encuentra los focos de la elipse$\dfrac{\left( x - 2 \right)^2}{4} + \dfrac{\left( y + 3 \right)^2}{29} = 1$.

Solución

La elipse es vertical con una ecuación de la forma$\dfrac{\left( x - h \right)^2}{b^2} + \dfrac{\left( y - k \right)^2}{a^2} = 1$.
El centro está en ($h$,$k$) = (2, -3). Los focos están en ($h$,$k \pm c$).

Para encontrar la longitud$c$ utilizamos$b^2 = a^2 - c^2$.
Sustituyendo da$4 = 29 - c^2$ o$c = \sqrt {25} = 5$.

La elipse tiene focos (2, -3 ± 5), o (2, -8) y (2, 2).

Ejemplo$\PageIndex{9}$

Encuentra la forma estándar de la ecuación para una elipse con focos (-1,4) y (3,4) y longitud del eje mayor 10.

Solución

Dado que los focos difieren en las$x$ coordenadas, la elipse es horizontal con una ecuación de la forma$\dfrac{\left( x - h \right)^2}{a^2} + \dfrac{\left( h - k \right)^2}{b^2} = 1$.
El centro está en el punto medio de los focos$\left( \dfrac{x_1 + x_2}{2},\dfrac{y_1 + y_2}{2} \right) = \left( \dfrac{\left( - 1 \right) + 3}{2},\dfrac{4 + 4}{2} \right) = \left( 1,4 \right)$.
El valor de$a$ es la mitad de la longitud del eje mayor:\[a = \dfrac{1}{2}(10) = 5\nonumber\]
El valor de$c$ es la mitad de la distancia entre los focos:\[c = \dfrac{1}{2}(3 - ( - 1)) = \dfrac{1}{2}(4) = 2\nonumber\]
Para encontrar la longitud$b$ utilizamos${b^2} = {a^2} - {c^2}$. Sustituyendo a y c da$b^2 = 5^2 - 2^2$ = 21.

La ecuación de la elipse en forma estándar es\[\dfrac{\left( x - 1 \right)^2}{5^2} + \dfrac{\left( y - 4 \right)^2}{21} = 1\text{ or }\dfrac{\left( x - 1 \right)^2}{25} + \dfrac{\left( y - 4 \right)^2}{21} = 1\nonumber\]

Ejercicio$\PageIndex{3}$

Encuentra la forma estándar de la ecuación para una elipse con foco (2,4), vértice (2,6) y centro (2,1).

Contestar: El vértice, el centro y el foco tienen el mismo$x$ valor, por lo que es una elipse vertical.
Usando el vértice y el centro,\[a = 6 – 1 = 5\nonumber\]
Usando el centro y el enfoque,\[c = 4 – 1 = 3\nonumber\]
\[b^2 = 5^2 - 3^2\quad b = 4\nonumber\]
\[\dfrac{\left( x - 2 \right)^2}{16} + \dfrac{\left( y - 1 \right)^2}{25} = 1\nonumber\]

Órbitas Planetarias

Durante mucho tiempo se pensó que las órbitas planetarias alrededor del sol eran circulares. Alrededor de 1600, Johannes Kepler descubrió que eran realmente elípticos (Técnicamente, son aproximadamente elípticos. Las órbitas de los planetas no son exactamente elípticas debido a las interacciones entre sí y con otros cuerpos celestes.). Su primera ley del movimiento planetario dice que los planetas viajan alrededor del sol en una órbita elíptica con el sol como uno de los focos. La longitud del eje mayor se puede encontrar midiendo el afelio del planeta, su mayor distancia del sol, y el perihelio, su distancia más corta del sol, y sumarlos juntos.

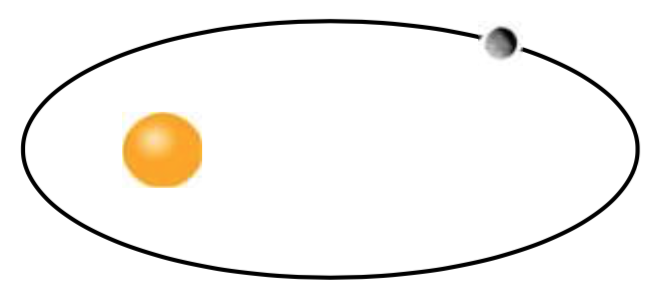
$2019-07-29 11.56.12.png$

Ejemplo$\PageIndex{10}$

El afelio de Mercurio es de 35.98 millones de millas y su perihelio es de 28.58 millones de millas. Escribe una ecuación para la órbita de Mercurio.

Solución

Deje que el centro de la elipse sea (0,0) y su eje mayor sea horizontal para que la ecuación tenga forma$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$.

La longitud del eje mayor está$2a = 35.98 + 28.58 = 64.56$ dando$a = 32.28$ y$a^2 = 1041.9984$.

Dado que el perihelio es la distancia desde el foco a un vértice, podemos encontrar la distancia entre los focos restando el doble del perihelio de la longitud del eje mayor:$2c = 64.56 - 2\left( 28.58 \right) = 7.4$ dando$c = 3.7$.
Sustitución de$a$ y$c$ en$b^2 = a^2 - c^2$ rendimientos$b^2 = 32.28^2 - 3.7^2 = 1028.3084$.

La ecuación es\[\dfrac{x^2}{1041.9984} + \dfrac{y^2}{1028.3084} = 1\nonumber\]

Temas Importantes de esta Sección

Definición de elipse
Ecuaciones de elipse en forma estándar
Focos de elipse
Aplicaciones de elipses