9.4: Cónicas en Coordenadas Polares

En las secciones anteriores, definimos cada cónica de una manera diferente, pero cada una implicaba la distancia entre un punto en la curva y el foco. En la sección anterior, la parábola se definió usando el foco y una línea llamada directrix. Resulta que todas las secciones cónicas (círculos, elipses, hipérbolas y parábolas) se pueden definir usando una sola relación.

SECCIONES CONICAS Definición GENERAL

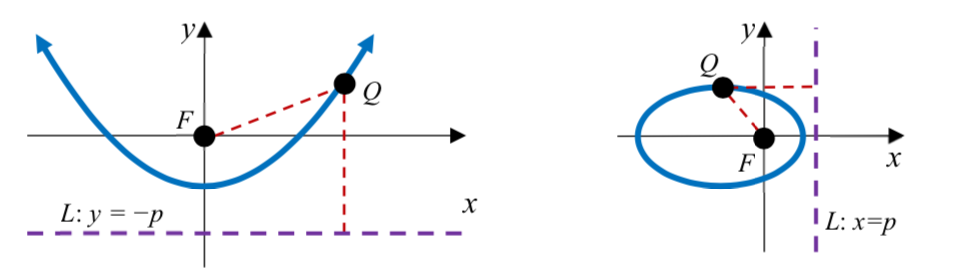
Una sección cónica se puede definir colocando un punto fijo en el origen,\(F\left( 0,0 \right)\), llamado foco, y dibujando una línea L llamada directrix en\(x = \pm p\) o\(y = \pm p\). La sección cónica es el conjunto de todos los puntos\(Q\left( x,y \right)\) para los cuales la relación de la distancia de\(Q\)\(F\) a la distancia de\(Q\) a la directrix es alguna constante positiva \(e\), llamada la excentricidad. En otras palabras,\[\dfrac{d\left( Q,F \right)}{d(Q,L)} = e\]

Advertencia: la excentricidad,\(e\), no es la constante de Euler\(e \approx 2.71828\) que estudiamos con exponenciales

La forma polar de una cónica

Para crear una ecuación general para una sección cónica usando la definición anterior, usaremos coordenadas polares. Representar\(Q\left( x,y \right)\) en coordenadas polares así\(\left( x,y \right) = \left( r\cos (\theta ), r\sin (\theta ) \right)\). Por ahora, nos centraremos en el caso de una directrix horizontal en\(y = - p\), como en la imagen de arriba a la izquierda.

La distancia desde el foco hasta el punto\(Q\) en polar es justa\(r\).
La distancia desde el punto\(Q\) a la directrix\(y = - p\) es\(r\sin (\theta ) - ( - p) = p + r\sin (\theta )\)

La relación de estos debe ser la excentricidad constante e, por lo que

\[\dfrac{d\left( Q,F \right)}{d(Q,L)} = e\nonumber\]Sustituyendo en las expresiones las distancias,
\[\dfrac{r}{p + r\sin (\theta )} = e\nonumber\]

Para tener una ecuación polar estándar, necesitamos resolver para r. Empezar por borrar la fracción.

\[r = e\left( {p + r\sin (\theta )} \right)\nonumber\]Distribuir
\[r = ep + er\sin (\theta )\nonumber\] Mover términos con\(r\) a la izquierda
\[r - er\sin (\theta ) = ep\nonumber\] Factorizar la\(r\)
\[r\left( 1 - e\sin (\theta ) \right) = ep\nonumber\] división
\[r = \dfrac{ep}{1 - e\sin (\theta )}\nonumber\]

Podríamos repetir el mismo enfoque para una directrix en\(y = p\) y para las directrices verticales para obtener las ecuaciones polares a continuación.

ECUACIÓN POLAR PARA UNA SECCIÓN CONICA

Una sección cónica con un enfoque en el origen, excentricidad\(e\) y directrix en\(x = \pm p\) o\(y = \pm p\) tendrá ecuación polar:

\[r = \dfrac{ep}{1 \pm e\sin (\theta )}\text{ when the directrix is }y = \pm p\]

\[r = \dfrac{ep}{1 \pm e\cos (\theta )}\text{ when the directrix is }x = \pm p\]

Ejemplo\(\PageIndex{1}\)

Escribe la ecuación polar para una sección cónica con excentricidad 3 y directrix en\(x = 2\).

Solución

Nos dan\(e = 3\) y\(p = 2\). Dado que la directrix es vertical y a un\(x\) valor pos itivo, utilizamos la ecuación que involucra cos con el signo positivo.

\[r = \dfrac{(3)(2)}{1 + 3\cos (\theta )} = \dfrac{6}{1 + 3\cos (\theta )}\nonumber\]

Graficar que el uso de la tecnología revela que es una ecuación para una hipérbola.

Ejercicio\(\PageIndex{1}\)

Escribe una ecuación polar para una cónica con excentricidad 1 y directrix en\(y = - 3\).

Contestar

\[r = \dfrac{(1)(3)}{1 - \sin(\theta)}\quad r = \dfrac{3}{1 - \sin (\theta)}\nonumber\]

Relacionar la ecuación polar con la forma

Probablemente no era obvio para usted que la ecuación polar en el último ejemplo daría la gráfica de una hipérbola. Para explorar la relación entre la ecuación polar y la forma, intentaremos convertir la ecuación polar en una cartesiana. Por simplicidad, consideraremos el caso donde está la directrix\(x = 1\).

\[r = \dfrac{e}{1 + e\cos (\theta )}\nonumber\]Multiplicar por el denominador
\[r\left( 1 + e\cos (\theta ) \right) = e\nonumber\] Reescribir\(\cos (\theta ) = \dfrac{x}{r}\)
\[r\left( 1 + e\dfrac{x}{r} \right) = e\nonumber\] Distribuir
\[r + ex = e\nonumber\] Aislar\(r\)
\[r = e - ex\nonumber\] Cuadrado ambos lados
\[r^2 = \left( e - ex \right)^2\nonumber\] Reescribir\(r^2 = x^2 + y^2\) y expandir
\[x^2 + y^2 = e^2 - 2e^2x + e^2x^2\nonumber\] Mover términos variables a la izquierda
\[x^2 + 2e^2x - e^2x^2 + y^2 = e^2\nonumber\] Combinar términos similares
\[x^2(1 - e^2) + 2e^2x + y^2 = e^2\nonumber\]

Podríamos continuar, completando el cuadrado con los\(x\) términos, para eventualmente reescribir esto en la forma estándar como\(\left(\frac{(1-e^{2})^{2}}{e^{2}} \right)\left(x-\frac{e^{2}}{1-e^{2}} \right)^{2}+\left(\frac{1-e^{2}}{e^{2}} \right)y^{2}=1\), pero felizmente no hay necesidad de que hagamos eso.

En la ecuación\(x^2(1 - e^2) + 2e^2x + y^2 = e^2\), podemos ver que:
Cuando\(e < 1\), los coeficientes de ambos\(x^2\) y\(y^2\) son positivos, resultando en elipse.
Cuando\(e > 1\), el coeficiente de\(x^2\) es negativo mientras que el coeficiente de\(y^2\) es positivo, resultando en una hipérbola.
Cuando\(e = 1\), el\(x^2\) caerá fuera de la ecuación, resultando en una parábola.

RELACIÓN ENTRE LA ECUACIÓN POLAR DE UNA CÓNICA Y SU FORMA

Para una sección cónica con un enfoque en el origen, excentricidad\(e\), y directrix en\(x = \pm p\) o\(y = \pm p\),

cuando\(0 < e < 1\), la gráfica es una elipse
cuando\(e = 1\), la gráfica es una parábola
cuando\(e > 1\), la gráfica es una hipérbola

Tomando un enfoque más intuitivo, fíjate que si\(e < 1\), el denominador siempre\(1 + e\cos (\theta )\) será positivo y así siempre\(r\) será positivo. Esto significa que la distancia radial\(r\) es definida y finita para cada valor de\(\theta\), incluyendo\(\dfrac{\pi }{2}\), sin roturas. La única cónica con esta característica es una elipse.

Si\(e = 1\), el denominador será positivo para todos los valores de\(\theta\), excepto\( - \pi \) donde el denominador es 0 y no\(r\) está definido. Esto encaja con una parábola, que tiene un punto en cada ángulo excepto en el ángulo que apunta a lo largo del eje de simetría lejos del vértice.

Si\(e > 1\), entonces el denominador será cero en dos ángulos distintos de\( \pm \dfrac{\pi }{2}\), y\(r\) será negativo para un conjunto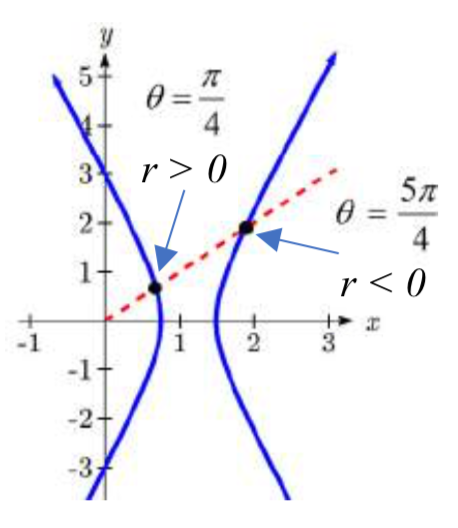 de\(\theta\) valores. Esta división de los valores de radio positivos y negativos daría como resultado dos ramas distintas de la gráfica, ajustándose con una hipérbola.

Ejemplo\(\PageIndex{2}\)

Para cada una de las siguientes cónicas con enfoque en el origen, identifique la forma, la directriz y la excentricidad.

a.\(r = \dfrac{8}{1 - 2\sin (\theta )}\)
b.\(r = \dfrac{6}{3 - 2\cos (\theta )}\)
c.\(r = \dfrac{8}{5 + 5\sin (\theta )}\)

Solución

a. Esta ecuación ya está en forma estándar\(r = \dfrac{ep}{1 \pm e\sin (\theta )}\) para una cónica con directrix horizontal en\(y = - p\).
La excentricidad es el coeficiente de\(\sin (\theta )\), entonces\(e = 2\).
Ya que\(e = 2 > 1\), la forma será una hipérbola.

Mirando el numerador,\(ep = 8\), y sustituyendo\(e = 2\) da\(p = 4\). La directrix es\(y = - 4\).

b. Esta ecuación no está en forma estándar, ya que la constante en el denominador no es 1. Para ponerlo en forma estándar, podemos multiplicar el numerador y el denominador por 1/3.

\[r = \dfrac{6}{3 - 2\cos (\theta )} \cdot \dfrac{\dfrac{1}{3}}{\dfrac{1}{3}} = \dfrac{6\left( \dfrac{1}{3} \right)}{\left( 3 - 2\cos (\theta ) \right)\left( \dfrac{1}{3} \right)} = \dfrac{2}{1 - \dfrac{2}{3}\cos (\theta )}\nonumber\]

Esta es la forma estándar para una cónica con directrix vertical\(x = - p\). La excentricidad es el coeficiente encendido\(\cos (\theta )\), entonces\(e = \dfrac{2}{3}\).
Ya que\(0 < e < 1\), la forma es una elipse.

Mirando el numerador,\(ep = 2\), entonces\(\dfrac{2}{3}p = 2\), dando\(p = 3\). La directrix es\(x = - 3\).

c. Esta ecuación tampoco está en forma estándar. Multiplicar el numerador y denominador por 1/5 lo pondrá en forma estándar.

\[r = \dfrac{8}{5 + 5\sin (\theta )} \cdot \dfrac{\dfrac{1}{5}}{\dfrac{1}{5}} = \dfrac{8\left( \dfrac{1}{5} \right)}{\left( 5 + 5\sin (\theta ) \right)\left( \dfrac{1}{5} \right)} = \dfrac{\dfrac{8}{5}}{1 + \sin (\theta )}\nonumber\]

Esta es la forma estándar para una cónica con directrix horizontal en\(y = p\).
La excentricidad es el coeficiente encendido\(\sin (\theta )\), entonces\(e = 1\). La forma será una parábola.

Mirando al numerador,\(ep = \dfrac{8}{5}\). Ya que\(e = 1\),\(p = \dfrac{8}{5}\). La directrix es\(y = \dfrac{8}{5}\).

Observe que dado que la directrix está por encima del foco en el origen, la parábola se abrirá hacia abajo.

Ejercicio\(\PageIndex{2}\)

Identificar la forma, la directrix y la excentricidad de\(r = \dfrac{9}{4 + 2\cos (\theta )}\)

Contestar

Podemos convertir a forma estándar multiplicando la parte superior e inferior por\(\dfrac{1}{4}\).
\[r = \dfrac{\dfrac{9}{4}}{1 + \dfrac{1}{2}\cos (\theta )}\nonumber\]Excentricidad =\(\dfrac{1}{2}\), por lo que la forma es una elipse.
El numerador es\[ep = \dfrac{1}{2}p = \dfrac{9}{4}\nonumber\] La directrix es\[x = \dfrac{9}{2}\nonumber\]

Graficando Cónicas desde la Forma Polar

Identificar características adicionales de una cónica en forma polar puede ser un desafío, lo que hace que la gráfica sin tecnología sea igualmente desafiante. Podemos utilizar nuestra comprensión de las formas cónicas de secciones anteriores para ayudarnos.

Ejemplo\(\PageIndex{3}\)

Esbozar una gráfica\(r = \dfrac{3}{1 - 0.5\sin (\theta )}\) y escribir su ecuación cartesiana.

Solución

Esto está en forma estándar, y podemos identificarlo\(e = 0.5\), por lo que la forma es una elipse.
Del numerador,\(ep = 3\), así\(0.5p = 3\), dando p = 6. La directrix es\(y = - 6\).

Para bosquejar una gráfica, ¿podemos comenzar evaluando la función a unos pocos convenientes? valores, y encontrar las coordenadas cartesianas correspondientes.

\[\theta = 0\quad r = \dfrac{3}{1 - 0.5\sin (0)} = \dfrac{3}{1} = 3\quad (x,y) = (3,0)\nonumber\]
\[\theta = \dfrac{\pi }{2}\quad r = \dfrac{3}{1 - 0.5\sin \left( \dfrac{\pi }{2} \right)} = \dfrac{3}{1 - 0.5} = 6\quad (x,y) = (0,6)\nonumber\]
\[\theta = \pi \quad r = \dfrac{3}{1 - 0.5\sin (\pi )} = \dfrac{3}{1} = 3\quad (x,y) = ( - 3,0)\nonumber\]
\[\theta = \dfrac{3\pi }{2}\quad r = \dfrac{3}{1 - 0.5\sin \left( \dfrac{3\pi }{2} \right)} = \dfrac{3}{1 + 0.5} = 2\quad (x,y) = (0, - 2)\nonumber\]

Trazar estos puntos y recordar el origen es uno de los focos que da una idea de la forma, en la que podríamos esbozar. Para obtener una comprensión b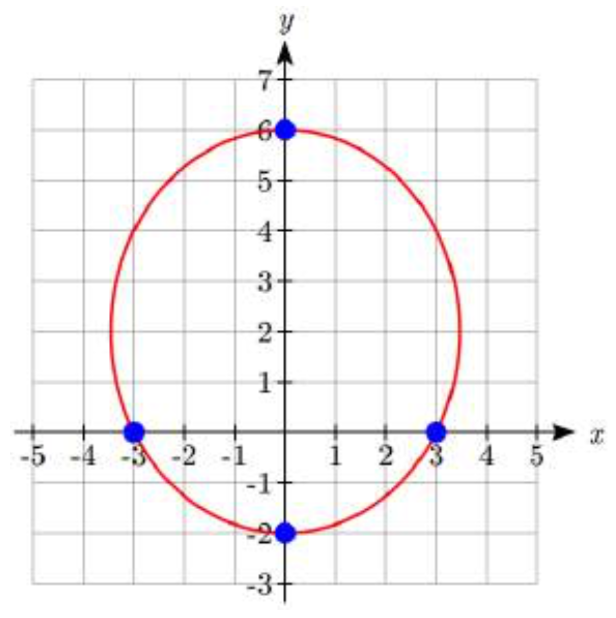 etter de la forma, podríamos usar estas características para encontrar más.

Los vértices están en (0, -2) y (0, 6), por lo que el centro debe estar a medio camino entre, at\(\left( 0,\dfrac{ - 2 + 6}{2} \right)\) = (0, 2). Dado que los vértices están a una distancia a del centro,\(a = 6 – 2 = 4\).

Un foco está en (0, 0), una distancia de 2 desde el centro, así\(c = 2\), y el otro foco debe estar 2 por encima del centro, en (0, 4).

Ahora podemos resolver para b:\(b^2 = a^2 - c^2\), entonces\(b^2 = 4^2 - 2^2 = 10\), de ahí\(b = \pm \sqrt {10} \). Los puntos finales del eje menor estarían en\(\left( - \sqrt {10} ,2 \right)\) y\(\left( \sqrt {10} ,2 \right)\).

Ahora podemos usar el centro,\(a\), y\(b\) para escribir la ecuación cartesiana para esta curva:
\[\dfrac{x^2}{10} + \dfrac{(y - 2)^2}{16} = 1\nonumber\]

Ejercicio\(\PageIndex{3}\)

Esboce una gráfica\(r = \dfrac{6}{1 + 2\cos (\theta )}\) e identifique las características importantes.

Contestar

La excentricidad es\(e = 2\), por lo que la gráfica de la ecuación es una hipérbola. La directrix es\(x = 3\). Dado que la directrix es una línea vertical y el foco está en el origen, la hipérbola es horizontal.
\[\theta = 0\quad r = \dfrac{6}{1 + 2\cos (0)} = \dfrac{6}{1 + 2} = 2\quad (x,y) = (2,0)\nonumber\]
\[\theta = \dfrac{\pi }{2}\quad r = \dfrac{6}{1 + 2\cos \left( \dfrac{\pi }{2} \right)} = \dfrac{6}{1} = 6\quad (x,y) = (0,6)\nonumber\]
\[\theta = \pi \quad r = \dfrac{6}{1 + 2\cos (\pi )} = \dfrac{6}{1 - 2} = - 6\quad (x,y) = (6,0)\nonumber\]
\[\theta = \dfrac{3\pi }{2}\quad r = \dfrac{6}{1 + 2\cos \left( \dfrac{3\pi }{2} \right)} = \dfrac{6}{1} = 6\quad (x,y) = (0, - 6)\nonumber\]

Trazando esos puntos, podemos conectar los tres de la izquierda con una curva suave para formar una rama de la hipérbola, y la 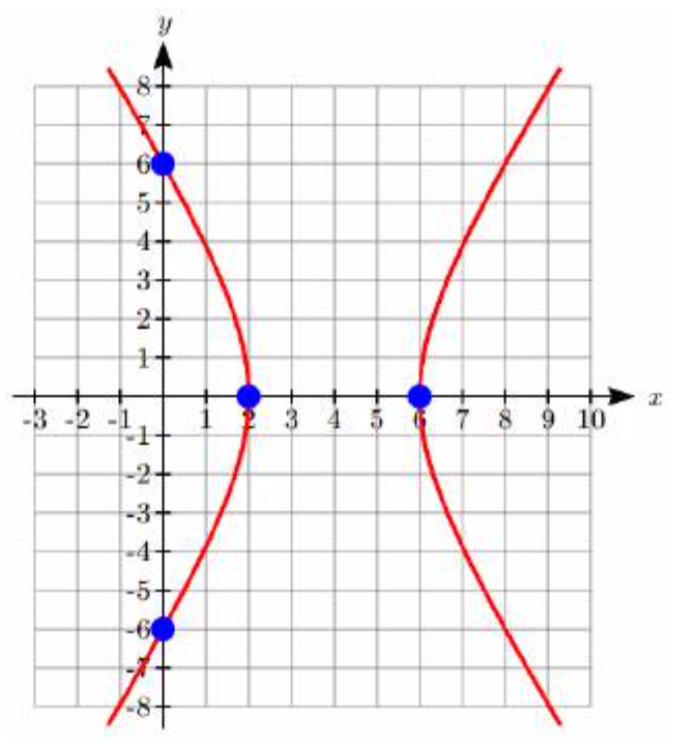otra rama será una imagen especular que pasa por el último punto.

Los vértices están en (2, 0) y (6, 0).

El centro de la hipérbola estaría en el punto medio de los vértices, en (4, 0).
Los vértices están a una\(a = 2\) distancia del centro.
El foco en el origen está a una\(c = 4\) distancia del centro.
Resolviendo para\(b\),\(b^2 = 4^2 - 2^2 = 12\). \(b = \pm \sqrt {12} = \pm 2 \sqrt 3 \).

Las asíntotas serían\(y = \pm \sqrt 3 \left( x - 4 \right)\).

La ecuación cartesiana de la hipérbola sería:
\(\dfrac{\left( x - 4 \right)^2}{4} - \dfrac{y^2}{12} = 1\)

Temas Importantes de esta Sección

• Ecuaciones polares para secciones cónicas
• Excentricidad y Directrix
• Determinar la forma de una sección cónica polar