9.4.4E: Cónicas en Coordenadas Polares (Ejercicios)

Sección 9.4 Ejercicios

En los problemas 1—8, encuentra la excentricidad y directrix, luego identifica la forma de la cónica.

1. \(r = \dfrac{12}{1 + 3\cos (\theta )}\)

2. \(r = \dfrac{4}{1 - \sin (\theta )}\)

3. \(r = \dfrac{2}{4 - 3\sin (\theta )}\)

4. \(r = \dfrac{7}{2 - \cos (\theta )}\)

5. \(r = \dfrac{1}{5 - 5\cos (\theta )}\)

6. \(r = \dfrac{6}{3 + 8\cos (\theta )}\)

7. \(r = \dfrac{4}{7 + 2\cos (\theta )}\)

8. \(r = \dfrac{16}{4 + 3\sin (\theta )}\)

En los problemas 9—14, encuentra una ecuación polar para una cónica que tenga un foco en el origen con las características dadas.

9. Directrix\(x = -4\), excentricidad\(e = 5\).

10. Directrix\(y = -2\), excentricidad\(e = 3\).

11. Directrix\(y = 3\), excentricidad\(e = \dfrac{1}{3}\).

12. Directrix\(x = 5\), excentricidad\(e = \dfrac{3}{4}\).

13. Directrix\(y = -2\), excentricidad\(e = 1\).

14. Directrix\(x = -3\), excentricidad\(e = 1\).

En los problemas 15—20, esboza una gráfica de la cónica. Usa la gráfica para ayudarte a encontrar características importantes y escribir una ecuación cartesiana para la cónica.

15. \(r = \dfrac{9}{1 - 2\cos (\theta )}\)

16. \(r = \dfrac{4}{1 + 3\sin (\theta )}\)

17. \(r = \dfrac{12}{3 + \sin (\theta )}\)

18. \(r = \dfrac{15}{3 - 2\cos (\theta )}\)

19. \(r = \dfrac{6}{1 + \cos (\theta )}\)

20. \(r = \dfrac{4}{1 - \sin (\theta )}\)

21. Al inicio del capítulo, definimos una elipse como el conjunto de todos los puntos\(Q\) para los que la suma de la distancia desde cada foco a\(Q\) es constante. Matemáticamente,\(d\left( Q, F_1 \right) + d\left( Q, F_2 \right) = k\). No es obvio que esta definición y la que se proporciona en esta sección que involucra la directrix estén relacionadas. En este ejercicio, comenzaremos con la definición de esta sección e intentaremos derivar la fórmula anterior a partir de ella.

a. Dibuja una elipse con focos en\(\left( c,0 \right)\) y\(\left( - c,0 \right)\), vértices en\(\left( a,0 \right)\) y\(\left( - a,0 \right)\), y directrices en\(x = p\) y\(x = - p\). Etiquetar los focos\(F_1\) y\(F_2\). Etiquetar las directrices\(L_1\) y\(L_2\). Etiquete algún punto\(\left( x,y \right)\) en la elipse\(Q\).
b. encontrar fórmulas para\(d\left( Q,L_1 \right)\) y\(D\left( Q, L_2 \right)\) en términos de\(x\) y\(p\).
c. De la definición de cónica en esta sección,\(\dfrac{d\left( Q,F_1 \right)}{d\left( Q,L_1 \right)} = e\). De igual manera,\(\dfrac{d\left( Q,F_2 \right)}{d\left( Q,L_2 \right)} = e\) también. Utilice estas proporciones, con sus respuestas de la parte (b) anterior, para encontrar fórmulas para\(d\left( Q, F_1 \right)\) y\(D\left( Q, F_2 \right)\) en términos de\(e\),\(x\), y\(p\).
d. Demostrar que la suma\(d\left( Q, F_1 \right) + d\left( Q, F_2 \right)\),, es constante. Esto establece que las definiciones están conectadas.
e. Que\(Q\) sea un vértice. Encuentra las distancias\(d\left( Q, F_1 \right)\) y\(D\left( Q, F_2 \right)\) en términos de\(a\) y\(c\). Luego combina esto con tu resultado de la parte (d) para encontrar una fórmula para\(p\) en términos de\(a\) y\(e\).
f. Que\(Q\) sea un vértice. Encuentra las distancias\(D\left( Q, L_2 \right)\) y\(D\left( Q, F_2 \right)\) en términos de\(a\),\(p\), y\(c\). Usa la relación\(\dfrac{d\left( Q, F_2 \right)}{d\left( Q, L_2 \right)} = e\), junto con tu resultado de la parte (e), para encontrar una fórmula para\(e\) en términos de\(a\) y\(c\).

22. Cuando miramos por primera vez las hipérbolas, las definimos como el conjunto de todos los puntos Q para los que el valor absoluto de la diferencia de las distancias a dos puntos fijos es constante. Matemáticamente,\(\left| d\left( Q, F_1 \right) - d\left( Q, F_2 \right) \right| = k\). Utilizar un enfoque similar al del último ejercicio para obtener esta fórmula a partir de la definición dada en esta sección. Encuentra una fórmula para\(e\) en términos de\(a\) y\(c\).

Contestar

1. \(e = 3\). Directrix:\(x = 4\). Hipérbola.

3. \(e = 3/4\). Directrix:\(y = -2/3\). Elipse.

5. \(e = 1\). Directrix:\(x = -1/5\). Parábola.

7. \(e = 2/7\). Directrix:\(x. = 2\). Elipse.

9. \(r = \dfrac{20}{1 - 5\cos(\theta)}\)

11. \(r = \dfrac{1}{1 + \dfrac{1}{3} \sin(\theta)}\), o\(r = \dfrac{3}{3 + \sin(\theta)}\)

13. \(r = \dfrac{2}{1 - \sin(\theta)}\)

15. Hipérbola. Los vértices en (-9, 0) y (-3, 0) Centran en (-6, 0). \(a = 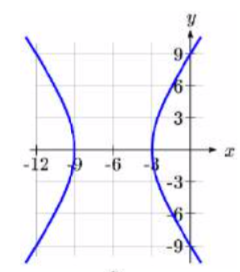3\),\(c = 6\), entonces\(b = \sqrt{27}\)

\(\dfrac{(x + 6)^2}{9} - \dfrac{y^2}{27} = 1\)

17. Elipse. Vértices en (0, 3) y (0, -6). Centro en (0, -1.5). \(a = 4.5\),\(c 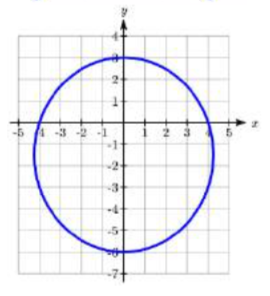= 1.5\),\(b = \sqrt{18}\).

\(\dfrac{x^2}{18} + \dfrac{(y + 1.5)^2}{20.25} = 1\)

19. Parábola. Vértice en (3, 0). \(p = 3\).

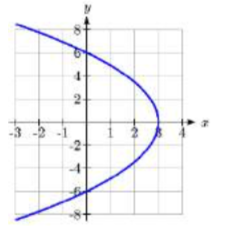
\(y^2 = 12(x - 3)\)

21. a).
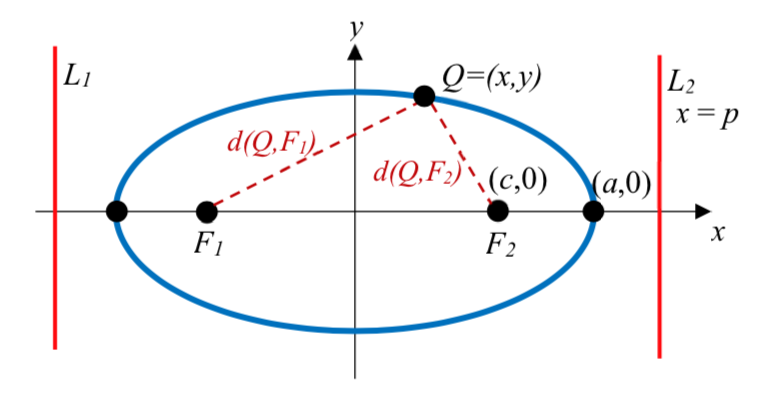
b). \(d(Q, L_1) = x -(-p) = x + p\),\(d(Q, L_2) = p - x\)
c). \(d(Q, F_1) = ed(Q, L_1) = e(x + p)\). \(d(Q, F_2) ed(Q, L_2) e(p - x)\)
d). \(d(Q, F_1) + d(Q, F_2) = e(x + p) + e(p - x) = 2ep\), una constante.
e). En\(Q = (a, 0)\),\(d(Q, F_1) = a - (-c) = a + c\), y\(d(Q, F_2) = a - c\), entonces\(d(Q, F_1) + d(Q, F_2) = (a + c) + (a - c) = 2a\).
Combinando con el resultado anterior,\(2ep = 2a\), así\(p = \dfrac{a}{e}\)
f). \(d(Q, F_2) = a - c\), y\(d(Q, L_2) = p - a\)
\(\dfrac{d(Q, F_2}{Q, L_2} =e\), entonces\(\dfrac{a - c}{p - a} = e\).
\(a - c = e (p - a)\). Utilizando el resultado de (e).
\(a - c = e(\dfrac{a}{e} - a)\)
\(a - c = a - ea\)
\(e = \dfrac{c}{a}\)