4.1: La ley de los senos

Última actualización
Guardar como PDF

Page ID: 117061

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La Ley de los senos se basa en relaciones de triángulo rectángulo que se pueden crear con la altura de un triángulo. A menudo, en este tipo de problemas, los ángulos se etiquetan con mayúsculas y sus lados correspondientes se etiquetan con letras minúsculas.

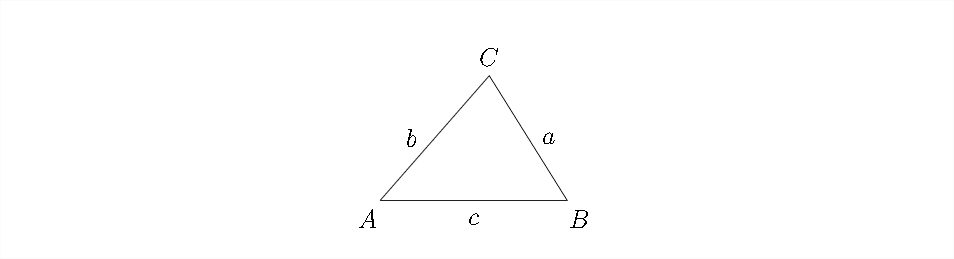
$clipboard_eac733ee8f364a15422bb0e27b3f1b8a8.png$

Si dejamos caer una perpendicular a la base del triángulo desde el punto del vértice en$\angle C$ este se crean dos triángulos rectos con los que podemos hacer uso de la trigonometría del triángulo rectángulo cubierta en el Capítulo 1. Esta perpendicular sería la altura del triángulo.

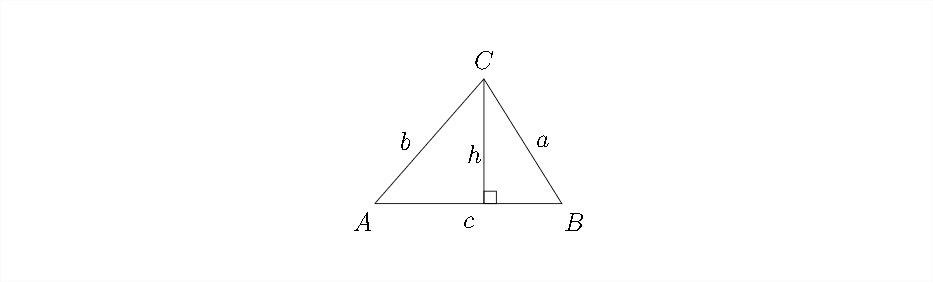
$clipboard_e7b09721a399178375fc67e4c99f94ca5.png$

La Ley de los senos se deriva de esta configuración y nos permite calcular el valor de lados y ángulos en un triángulo sin ángulo recto, a partir de información sobre lados y ángulos conocidos. Dados los triángulos rectos en el diagrama anterior, podemos ver que:
\ [ \ sin B=\ frac {h} {a}
\] y
\ [ \ sin A=\ frac {h} {b}
\]

Despejando el denominador en cada fracción, podemos ver que:
\ [ a\ sin b=h
\] y
\ [\ begin {array} {c}
b\ sin a=h\
\\ text {so}\\
a\ sin b=b\ sin A
\ end {array}
\]

Para poner esto en la forma en que normalmente se establece la Ley de los senos, podemos dividir en ambos lados de la expresión anterior por$a b$:
\ [ \ begin {array} {c}
a\ sin b=b\ sin A\
\ frac {a\ sin B} {a b} =\ frac {b\ sin A} {a b}\
\ frac {\ sin B} {b} =\ frac {\ sin A} {a}
\ end {array}
\] Un proceso similar mostrará que$\frac{\sin C}{c}$ es equivalente a$\frac{\sin B}{b}$ y$\frac{\sin A}{a} .$ El diagrama del que derivamos esto usó un triángulo agudo en el que todos los ángulos eran menores que
$90^{\circ} .$ El proceso para mostrar que esto es cierto para un triángulo obtuso (que tiene un ángulo mayor que$90^{\circ}$) es relativamente simple y se deja al lector para que lo descubra o busque en otro recurso.
La Ley de los senos
\ [ \ frac {\ sin A} {a} =\ frac {\ sin B} {b} =\ frac {\ sin C} {c}
\]

A veces es útil configurar un problema con las longitudes laterales en el numerador:
La Ley de los senos
\ [ \ frac {a} {\ sin A} =\ frac {b} {\ sin B} =\ frac {c} {\ sin C}
\]\

Resuelve el triángulo. Redondear longitudes laterales al más cercano$100^{\text {th }}$.

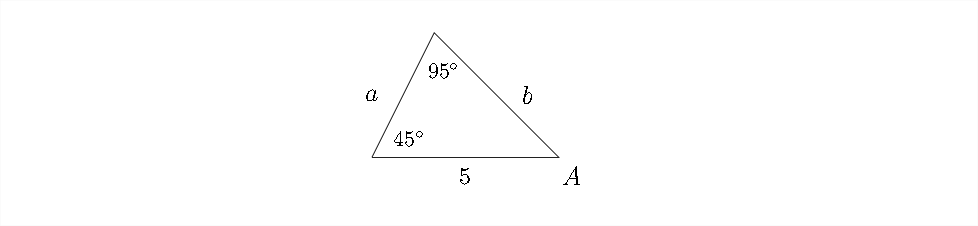
$clipboard_ecd7108ed631699e9328306b1877cc836.png$

En este problema nos dan dos ángulos y un lado. Es importante que el lado que nos dan corresponda a uno de los ángulos conocidos, de lo contrario no podríamos usar la Ley de los senos.

$clipboard_efd6162a6b041a9fc357f97e51d067642.png$

ya que conocemos dos de los ángulos, entonces el tercero solo será$180^{\circ}-\left(45^{\circ}+95^{\circ}\right)=$$180^{\circ}-140^{\circ}=40^{\circ}=\angle A .$ Para encontrar las longitudes de los lados desconocidos, usaremos la Ley de los senos. Deberíamos comenzar por elegir un par de ángulo lateral para el cual conocemos tanto el lado como el ángulo. En este caso, lo sabemos$\angle C=95^{\circ}$ y lado$c=5$
\ [ \ begin {array} {c}
\ frac {c} {\ sin C} =\ frac {b} {\ sin B}\\ sin B}
\\ frac {5} {\ sin 95^ {\ circ}} =\ frac {b} {\ sin 45^ {\ circ}}
\ end {array}
\] Si multiplicamos en ambos lados por$\sin 45^{\circ},$ entonces
\ [ \ sin 45^ {\ circ} *\ frac {5} {\ sin 95^ {\ circ}} =b
\]

Para llegar a un valor aproximado para$\sin 45^{\circ} * \frac{5}{\sin 95^{\circ}},$ podemos decir:
\ [ \ begin {array} {c}
0.7071 *\ frac {5} {0.9962}\ approx b\\
3.55\ approx b
\ end {array}
\] Para encontrar la longitud de lado$a,$ recomendaría que usemos la exacta par de ángulo lateral que se dio en el problema, en lugar de usar el valor aproximado de lado$b$ que acabamos de resolver para.

Esto hará que nuestro valor para lado sea$a$ más preciso:
\ [ \ begin {array} {c}
\ frac {c} {\ sin C} =\ frac {a} {\ sin A}\\ sin A}
\\ frac {5} {\ sin 95^ {\ circ}} =\ frac {a} {\ sin 40^ {\ circ}}
\ end {array}
\] Multiplicando en ambos lados por$\sin 40^{\circ},$ entonces
\ [ \ sin 40^ {\ circ} *\ frac {5} {\ sin 95^ {\ circ}} =a
\] Para llegar a un valor aproximado para$\sin 40^{\circ} * \frac{5}{\sin 95^{\circ}},$ podemos decir:
\ [ \ begin {array} {c}
0.6428 *\ frac {5} {0.9962}\ approx a\\
3.23\ approx a
\ end {array}
\]

\ begin {array} {lll}
\ ángulo A=40^ {\ circ} & a\ aproximadamente 3.23\\
\ ángulo B=45^ {\ circ} & b\ aprox 3.55\
\ ángulo C=95^ {\ circ} & c=5
\ end {array}

Ejemplo 2
Algunos problemas no vienen con diagramas:
Resuelve el triángulo si:$\quad \angle A=40^{\circ}, \quad \angle B=20^{\circ}, \quad a=2$
Redondear longitudes de lado al más cercano$100^{\text {th }}$.
Al igual que en el ejemplo anterior, podemos comenzar por encontrar la medida del tercer ángulo$\angle C .$ Esto sería$180^{\circ}-\left(40^{\circ}+20^{\circ}\right)=180^{\circ}-60^{\circ}=120^{\circ}=\angle C$
Para encontrar los lados faltantes, deberíamos usar el par completo de ángulos laterales que se da en el problema:$\angle A=40^{\circ}$ y$a=2$

Podemos encontrar lado$b$ primero o lado$c$ primero, no importa cual:
\ [ \ begin {array} {c}
\ frac {a} {\ sin A} =\ frac {b} {\ sin B}\\ sin B}\
\ frac {2} {\ sin 40^ {\ circ}} =\ frac {b} {\ sin 20^ {\ circ}}\\
\ sin 20^ {\ circ c} *\ frac {2} {\ sin 40^ {\ circ}} =b
\ end {array}
\] Entonces,
\ [ 0.3420 *\ frac {2} {0.6428}\ approx b
\] \ [ 1.06\ approx b
\]

Para lado$c:$
\ [ \ begin {array} {c}
\ frac {a} {\ sin A} =\ frac {c} {\ sin C}\\ sin C}
\\ frac {2} {\ sin 40^ {\ circ}} =\ frac {c} {\ sin 120^ {\ circ}}\
\ sin 120^ {\ circ} *\ frac {2} {\ sin 40^ ^ {\ circ}} =c
\ end {array}
\] Entonces,
\ [ 0.8660 *\ frac {2} {0.6428}\ aprox c
\] \ [ 2.69\ aprox c
\]

\ begin {array} {ll}
\ ángulo A=40^ {\ circ} & a=2\\
\ ángulo B=20^ {\ circ} & b\ aprox 1.06\
\ ángulo C=120^ {\ circ} & c\ aprox 2.69
\ end {array}

Ejercicios 4.1
En cada problema a continuación, resuelve el triángulo. Redondear longitudes laterales al más cercano$100^{t h}$

$clipboard_eb35eb9b7e4974af18f57af53957eaa70.png$

$clipboard_e2a41e1a1ec69a12f42d183fa5e3586eb.png$

$clipboard_eefcff0db20941dbb5f13172b2abfabe8.png$

7. $\quad \angle A=50^{\circ}, \quad \angle C=27^{\circ}, \quad a=3$
8. $\quad \angle B=70^{\circ}, \quad \angle C=10^{\circ}, \quad b=5$
9. $\quad \angle A=110^{\circ}, \quad \angle C=30^{\circ}, \quad c=3$
10. $\quad \angle A=50^{\circ}, \quad \angle B=68^{\circ}, \quad a=230$
11. $\quad \angle A=23^{\circ}, \quad \angle B=110^{\circ}, \quad c=50$
12. $\quad \angle A=22^{\circ}, \quad \angle B=95^{\circ}, \quad a=420$
13. $\quad \angle B=10^{\circ}, \quad \angle C=100^{\circ}, \quad c=11$
14. $\quad \angle A=30^{\circ}, \quad \angle C=65^{\circ}, \quad b=10$
15. $\quad \angle A=82^{\circ}, \quad \angle B=65.4^{\circ}, \quad b=36.5$
16. $\quad \angle B=28^{\circ}, \quad \angle C=78^{\circ}, \quad c=44$
17. $\quad \angle A=42^{\circ}, \quad \angle B=61^{\circ}, \quad a=12$
18. $\quad \angle A=42.5^{\circ}, \quad \angle B=71.4^{\circ}, \quad a=215$