4.2: La ley de los senos - El caso ambiguo

Última actualización
Guardar como PDF

Page ID: 117063

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En todos los ejemplos y problemas en Sección$4.1,$ notamos que siempre nos dieron dos ángulos y un lado, aunque podríamos usar la Ley de senos si nos dieran un ángulo y dos lados (siempre y cuando uno de los lados correspondiera al ángulo dado). Esto se debe a que cuando utilizamos la Ley de los senos para encontrar un ángulo, puede surgir una ambigüedad debido a que la función sinusoidal es positiva en el Cuadrante I y el Cuadrante II.

Vimos en el Capítulo 3 que surgen múltiples respuestas cuando utilizamos las funciones trigonométricas inversas. Para problemas en los que utilizamos la Ley de los senos dado un ángulo y dos lados, puede haber un posible triángulo, dos triángulos posibles o ningún triángulo posible. Hay seis escenarios diferentes relacionados con el caso ambiguo de la Ley de los senos: tres dan como resultado un triángulo, uno da como resultado dos triángulos y dos dan como resultado ningún triángulo.

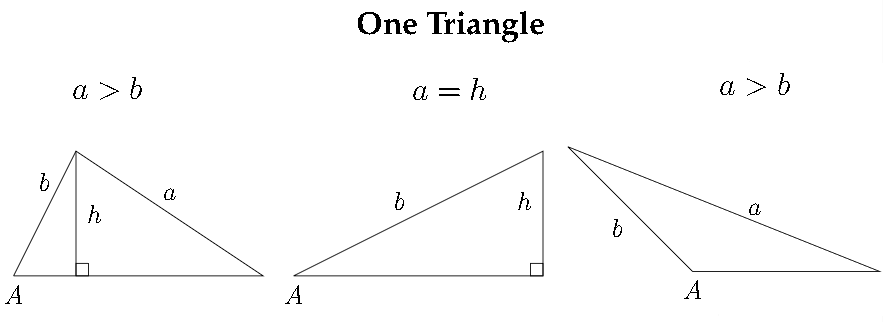
$clipboard_e484d6452533c6f71012450d87f72306e.png$

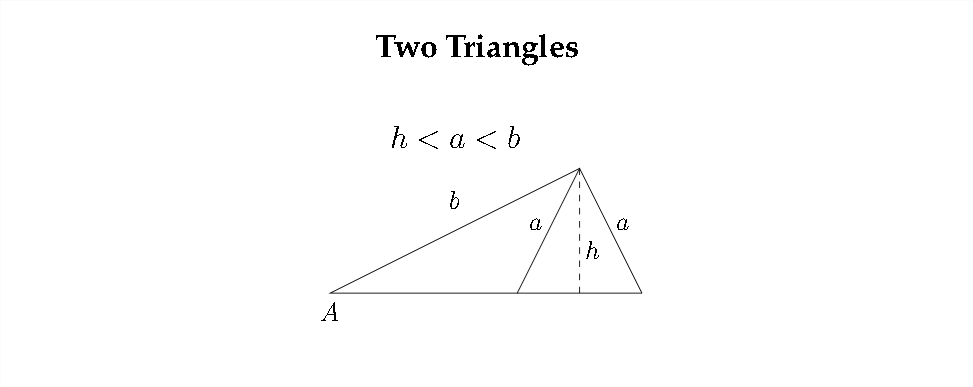
$clipboard_e96d08b746ff59d60400f67c7e7c76ef7.png$

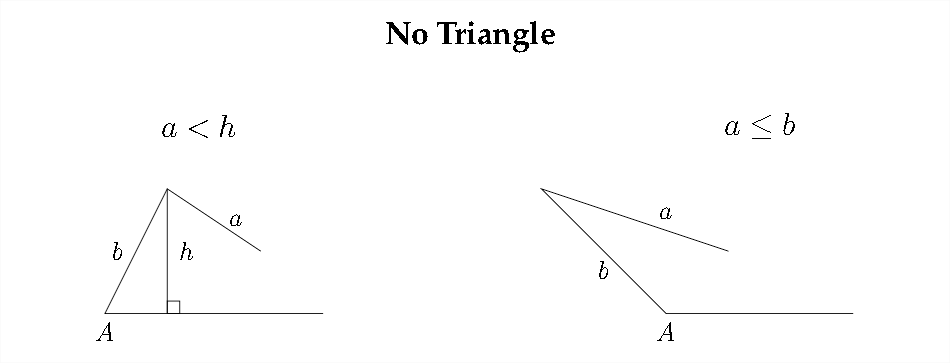
$clipboard_eca64508375b47cc3aba09765dadd6164.png$

Veremos tres ejemplos: uno para un triángulo, uno para dos triángulos y otro para ningún triángulos.

Ejemplo$\PageIndex{1}$

Resuelve el triángulo si:$\angle A=112^{\circ}, \quad a=45, \quad b=24$
Redondear los ángulos y longitudes laterales al más cercano$10^{t h}$

Solución

Usando la Ley de los senos, podemos decir que:

\ [\ begin {array} {c}
\ frac {\ sin 112^ {\ circ}} {45} =\ frac {\ sin B} {24}\
\ frac {0.9272} {45}\ approx\ frac {\ sin B} {24}\
24 *\ frac {0.9272} {45}\ approx\ sin B\
0.4945\ approx\ sin B
\ fin {matriz}
\]

Entonces, encontramos$\sin ^{-1}(0.4945) \approx 29.6^{\circ} .$ Recordar del Capítulo 3 que hay un ángulo del Cuadrante II que tiene$\sin \theta \approx 0.4945,$ con un ángulo de referencia de también$29.6^{\circ} . \mathrm{So}, \angle B$ podría ser$\approx 150.4^{\circ} .$ Sin embargo, con no$\angle A=112^{\circ},$ hay forma de que otro ángulo de$150.4^{\circ}$ encajaría dentro del mismo triángulo. Por esta razón, sabemos entonces que$\angle B$ debe ser$29.6^{\circ}$

\[ 29.6^{\circ} \approx B\]

Así que ahora

\ [\ begin {array} {c}
\ ángulo A=112^ {\ circ}\
\ ángulo B\ aprox 29.6^ {\ circ}\
\ nombre del operador {y}\ ángulo C=180^ {\ circ} -\ izquierda (112^ {\ circ} +29.6^ {\ circ}\ derecha) =180^ {\ circ} -141.6^ {\ circ} c}\ aproximadamente 38.4^ {\ circ}\\
\ ángulo C\ aproximadamente 38.4^ {\ circ}
\ final {matriz}\]

Ya lo sabemos$a=45$ y$b=24 .$ Para encontrar lado$c,$ recomendaría usar los valores más exactos posibles en el cálculo de la Ley de senos. Esto proporcionará el resultado más preciso en la búsqueda de la longitud del lado$c$

\ begin {array} {cc}
\ frac {45} {\ sin 112^ {\ circ}} =\ frac {c} {\ sin 38.4^ {\ circ}}\
\ frac {45} {0.9272}\ approx\ frac {c} {0.6211}\\
0.6211 *\ frac {45} {0.9272}\ approx c\\
30.1\ aprox c\\
\ ángulo A=112^ {\ circ} y a=45\\
\ ángulo B \ aprox 29.6^ {\ circ} & b=24\\
\ ángulo C\ aproximadamente 38.4^ {\ circ} & c\ aproximadamente 30.1
\ end {array}

Ejemplo$\PageIndex{2}$

Resuelve el triángulo si:$\angle A=38^{\circ}, \quad a=40, \quad b=52$
Redondear los ángulos y longitudes laterales al más cercano$10^{\text {th }}$.

Solución

Usando la Ley de los senos, podemos decir que:

\ [\ begin {array} {c}
\ frac {\ sin 38^ {\ circ}} {40} =\ frac {\ sin B} {52}\
\ frac {0.6157} {40}\ approx\ frac {\ sin B} {52}\
52 *\ frac {0.6157} {40}\ approx\ sin B\\
0.8004\ approx\ sin B
\ end {array}
\]

Así como en el ejemplo anterior, podemos encontrar$\sin ^{-1}(0.8004) \approx 53.2^{\circ} .$ Pero nuevamente, hay un ángulo del Cuadrante II cuyo seno tiene el mismo valor$\approx 0.8004$. El ángulo$126.8^{\circ}$ tiene un seno$\approx 0.8004$ y un ángulo de referencia de$53.2^{\circ} .$ Con$\angle A=38^{\circ},$ ambos ángulos$\left(53.2^{\circ} \text { and } 126.8^{\circ}\right)$ podrían caber potencialmente en el triángulo con ángulo$A$

Si volvemos a los diagramas que vimos anteriormente en esta sección, podemos ver cómo sucedería esto:

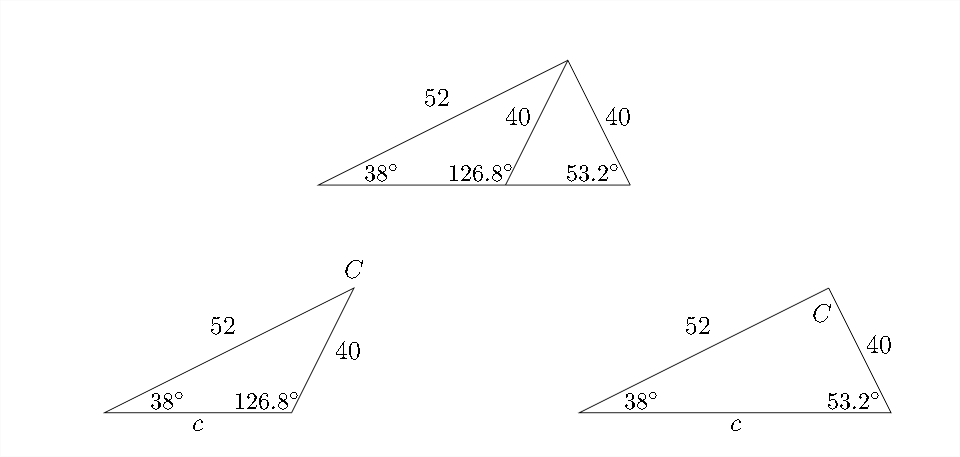
$clipboard_efd12136f6531749aa2a23d7e29cd3653.png$

En la primera posibilidad$\angle C$ estaría$\approx 15.2^{\circ}$
En la segunda posibilidad$\angle C$ sería$\approx 88.8^{\circ}$

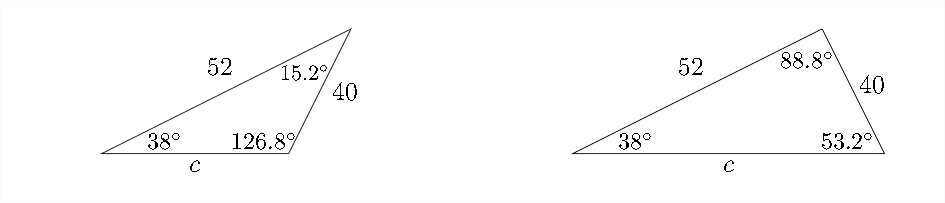
$clipboard_e790ef11af5293e522db1e3ce777d75a8.png$

Para encontrar las dos longitudes posibles para lado$c,$ necesitaremos resolver dos cálculos de Ley de senos, uno con$\angle C \approx 15.2^{\circ}$ y otro con el$\angle C \approx 88.8^{\circ}$

\ [\ begin {array} {c}
\ frac {40} {\ sin 38^ {\ circ}} =\ frac {c} {\ sin 15.2^ {\ circ}}\
\ frac {40} {0.6157}\ approx\ frac {c} {0.2622}\\
0.2622 *\ frac {40} {0.6157}\ c aprox\
17.0\ aprox c
\ final {array}
\]

Con$\angle C \approx 88.8^{\circ}$:

\ [\ frac {40} {\ sin 38^ {\ circ}} =\ frac {c} {\ sin 88.8^ {\ circ}}\\ circ}
\\ frac {40} {0.6157}\ approx\ frac {c} {0.9998}\\
0.9998 *\ frac {40} {0.6157}\ aprox c\\
65.0\ aprox c
\]

Entonces, nuestras dos posibles soluciones serían:
\ [\ begin {array} {lll}
\ angle A=38^ {\ circ} & a=40\
\ ángulo B\ approx 126.8^ {\ circ} & b=52\
\ ángulo C\ approx 15.2^ {\ circ} & c\ approx 17.0
\ end {array}
\]$\mathrm{OR}$
\ [\ ángulo A=38^ {\ circ}\ quad a=40
\]\ [\ begin {array} {lll}
\ ángulo B\ aproximadamente 53.2 ^ {\ circ} & b=52\
\ ángulo C\ aproximadamente 88.8^ {\ circ} & c\ aproximadamente 65.0
\ final {array}
\]

Ejemplo$\PageIndex{3}$

Resuelve el triángulo si:

\[\angle B=73^{\circ}, \quad b=51, \quad a=92.\]

Redondear los ángulos y longitudes de los lados al más cercano$10^{\text {th }}$.

Solución

Usando la Ley de los senos, podemos decir que:

\[ \frac{\sin 73^{\circ}}{51}=\frac{\sin A}{92}\]

\ [\ begin {array} {c}
\ frac {0.9563} {51}\ approx\ frac {\ sin A} {92}\
92 *\ frac {0.9563} {51}\ approx\ sin A\\
1.7251\ approx\ sin A
\ end {array}\]

Como vimos anteriormente, ningún ángulo de valor real tiene un seno mayor que$1 .$ Por lo tanto, ningún triángulo es posible.

Ejercicios

En cada problema, resuelve el triángulo. Redondear las longitudes de los lados al más cercano$100^{\text {th }}$ y el ángulo mide al más cercano$10^{\text {th }}$.

1. $\quad \angle A=50^{\circ}, \quad b=20, \quad a=32$
2. $\quad \angle B=40^{\circ}, \quad b=4, \quad c=3$
3. $\quad \angle A=43^{\circ}, \quad a=23, \quad b=29$
4. $\quad \angle C=20^{\circ}, \quad c=43, \quad a=55$
5. $\quad \angle B=62^{\circ}, \quad b=4, \quad a=5$
6. $\quad \angle A=75^{\circ}, \quad b=8, \quad a=3$
7. $\quad \angle B=24^{\circ}, \quad a=17, \quad b=8$
8. $\quad \angle A=40^{\circ}, \quad a=4, \quad c=5$
9. $\quad \angle A=108^{\circ}, \quad a=12, \quad b=7$
10. $\quad \angle B=117^{\circ}, \quad b=19.6, \quad c=10.5$
11. $\quad \angle A=42^{\circ}, \quad a=18, \quad c=11$
12. $\quad \angle C=27^{\circ}, \quad a=42, \quad c=37$
13. $\quad \angle C=125^{\circ}, \quad c=2.7, \quad b=5.2$
14. $\quad \angle B=115^{\circ}, \quad b=68, \quad a=92$
15. $\quad \angle A=43^{\circ}, \quad a=31, \quad b=37$
16. $\quad \angle A=28^{\circ}, \quad b=3.5, \quad a=4.3$
17. $\quad \angle C=132^{\circ}, \quad c=22, \quad b=16$
18. $\quad \angle B=114.2^{\circ}, \quad b=87.2, \quad a=12.1$
19. $\quad \angle B=52^{\circ}, \quad c=82.7, \quad b=70$
20. $\quad \angle C=65^{\circ}, \quad b=7.6, \quad c=7.1$