5.1: Graficando las Funciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 113484

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La primera función que vamos a graficar es la función seno. Describiremos una forma geométrica de crear la gráfica, utilizando el círculo unitario. Este es el círculo de radio$1 $ en el$xy$ plano -que consiste en todos los puntos$(x,y) $ que satisfacen la ecuación$x^2 + y^2 = 1 $.

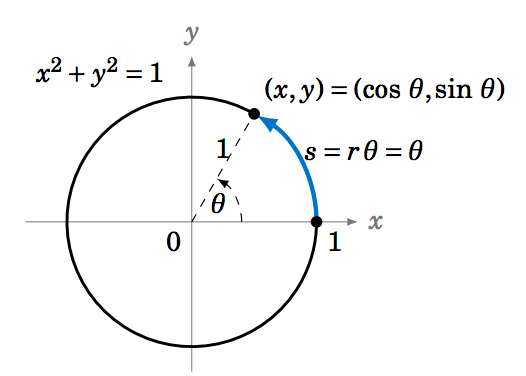
Vemos en la Figura 5.1.1 que cualquier punto del círculo unitario tiene coordenadas$(x,y)=(\cos\;\theta,\sin\;\theta) $, donde$\theta $ está el ángulo que el segmento de línea desde el origen hasta$(x,y) $ hace con el$x$ eje positivo (por definición de seno y coseno). Entonces, a medida que el punto$(x,y) $ va alrededor del círculo, su$y$ coordenada es$\sin\;\theta $.

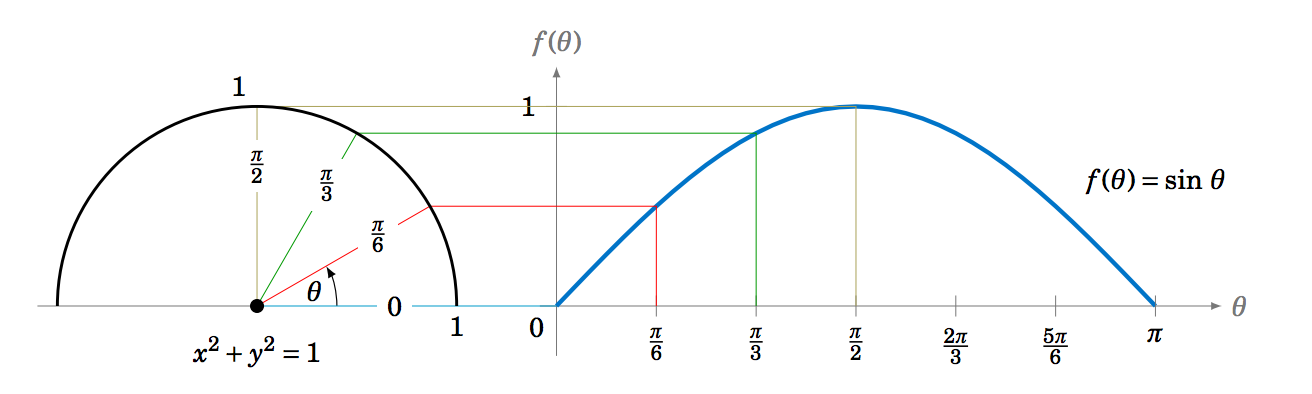
Así obtenemos una correspondencia entre las$y$ coordenadas -de puntos en el círculo unitario y los valores$f(\theta)=\sin\;\theta $, como lo muestran las líneas horizontales desde el círculo unitario hasta la gráfica de$f(\theta)=\sin\;\theta $ la Figura 5.1.2 para los ángulos$\theta = 0 $,$\tfrac{\pi}{6} $,$\tfrac{\pi}{3} $,$\tfrac{\pi}{2} $.

alt — Figura 5.1.2 Gráfico de la función sinusoidal basada en$y$ -coordenada de puntos en círculo unitario

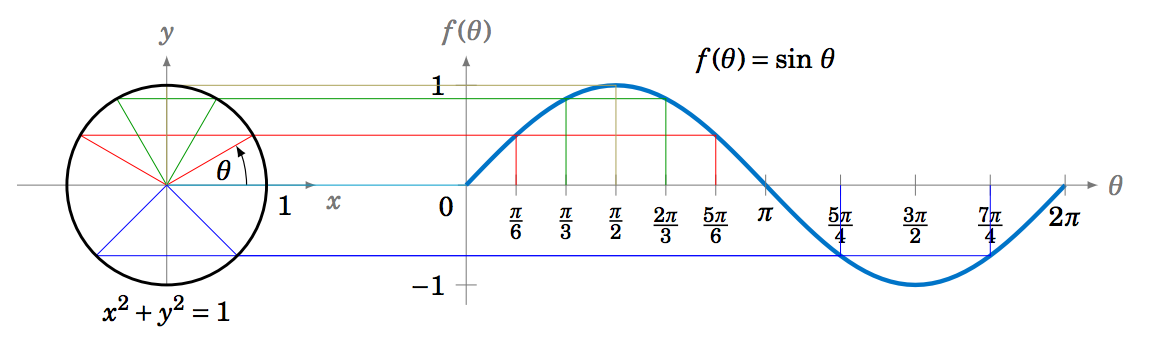
Podemos extender la imagen de arriba para incluir ángulos de$0 $ a$2\pi $ radianes, como en la Figura 5.1.3. Esto ilustra lo que a veces se llama la definición de círculo unitario de la función sinusoidal.

alt — Figura 5.1.3 Definición de círculo unitario de la función sinusoidal

Dado que las funciones trigonométricas repiten cada$2\pi $ radianes ($360^\circ$), obtenemos, por ejemplo, la siguiente gráfica de la función$y=\sin\;x $ para$x $ en el intervalo$[-2\pi , 2\pi]$:

alt — Figura 5.1.4 Gráfico de$y = \sin x$

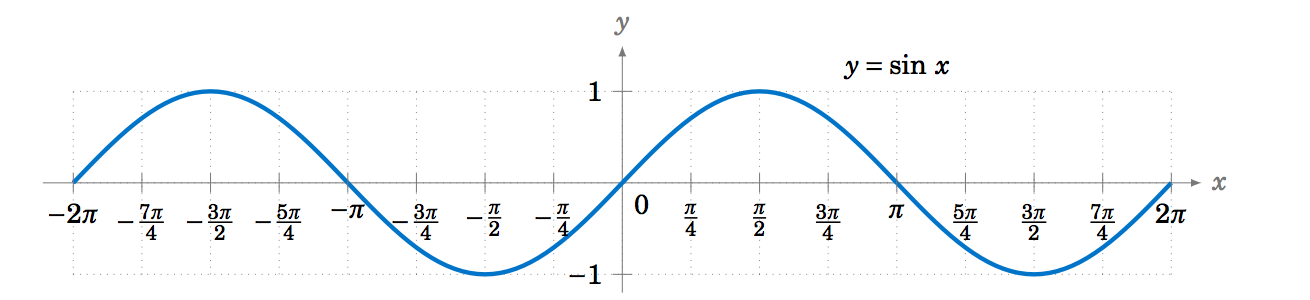
Para graficar la función coseno, podríamos volver a usar la idea de círculo unitario (usando la$x$ coordenada -de un punto que se mueve alrededor del círculo), pero hay una manera más fácil. Recordemos de la Sección 1.5 que$\cos\;x = \sin\;(x+90^\circ) $ para todos$x $. Entonces$\cos\;0^\circ $ tiene el mismo valor que$\sin\;90^\circ $,$\cos\;90^\circ $ tiene el mismo valor que$\sin\;180^\circ $,$\cos\;180^\circ $ tiene el mismo valor que$\sin\;270^\circ $, y así sucesivamente. En otras palabras, la gráfica de la función coseno es solo la gráfica de la función sinusoidal desplazada hacia la izquierda por$90^\circ = \pi/2 $ radianes, como en la Figura 5.1.5:

alt — Figura 5.1.5 Gráfico de$y = \cos x$

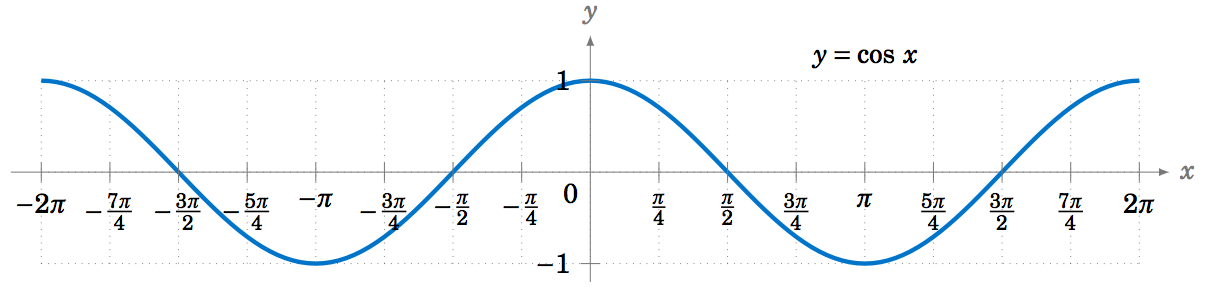
Para graficar la función tangente, utilice$\tan\;x = \frac{\sin\;x}{\cos\;x} $ para obtener la siguiente gráfica:

alt — Figura 5.1.6 Gráfico de$y = \tan x$

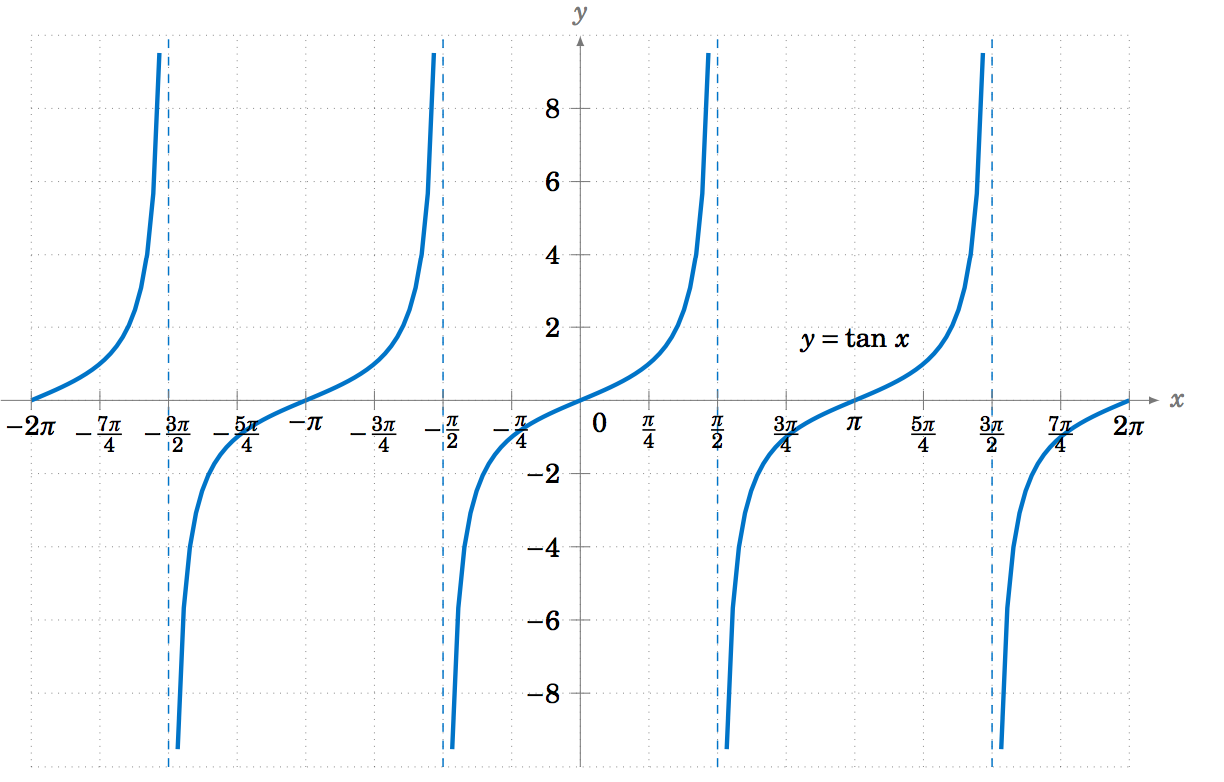
Recordemos que la tangente es positiva para los ángulos en QI y QIII, y es negativa en QII y QIV, y eso es de hecho lo que muestra la gráfica de la Figura 5.1.6. Sabemos que no$\tan\;x $ se define cuándo$\cos\;x = 0 $, es decir, en múltiplos impares de$\frac{\pi}{2}$:$x=\pm\,\frac{\pi}{2} $$\pm\,\frac{3\pi}{2} $$\pm\,\frac{5\pi}{2} $,,, etc. Podemos averiguar qué sucede cerca de esos ángulos observando las funciones seno y coseno. Por ejemplo, porque$x $ en QI cerca$\frac{\pi}{2} $,$\sin\;x $ y ambos$\cos\;x $ son positivos, con$\sin\;x $ muy cerca$1 $ y$\cos\;x $ muy cerca de$0 $, por lo que el cociente$\tan\;x = \frac{\sin\;x}{\cos\;x} $ es un número positivo que es muy grande. Y cuanto más$x $ se acerca$\frac{\pi}{2} $, más grande$\tan\;x $ se hace. Así,$x=\frac{\pi}{2} $ es una asíntota vertical de la gráfica de$y=\tan\;x $.

Así mismo, pues$x $ en la QII muy cerca$\frac{\pi}{2} $,$\sin\;x $ está muy cerca$1 $ y$\cos\;x$ es negativa y muy cercana a$0 $, por lo que el cociente$\tan\;x = \frac{\sin\;x}{\cos\;x} $ es un número negativo que es muy grande, y se hace más grande en la dirección negativa a medida que$x $ se acerca $\frac{\pi}{2} $. La gráfica muestra esto. Del mismo modo, obtenemos asíntotas verticales en$x=-\frac{\pi}{2} $,$x=\frac{3\pi}{2} $, y$x=-\frac{3\pi}{2} $, como en la Figura 5.1.6. Observe que la gráfica de la función tangente repite cada$\pi $ radianes, es decir, dos veces más rápido que las gráficas de repetición de seno y coseno.

Las gráficas de las funciones trigonométricas restantes se pueden determinar observando las gráficas de sus funciones recíprocas. Por ejemplo, usando solo$\csc\;x = \frac{1}{\sin\;x} $ podemos mirar la gráfica de$y=\sin\;x $ e invertir los valores. Obtendremos asíntotas verticales cuando$\sin\;x=0 $, es decir, en múltiplos de$\pi$:$x=0 $$\pm\,\pi $$\pm\,2\pi $,,, etc. La Figura 5.1.7 muestra la gráfica de$y=\csc\;x $, con la gráfica de$y=\sin\;x $ (la curva discontinua) para referencia.

alt — Figura 5.1.7 Gráfico de$y = \csc x$

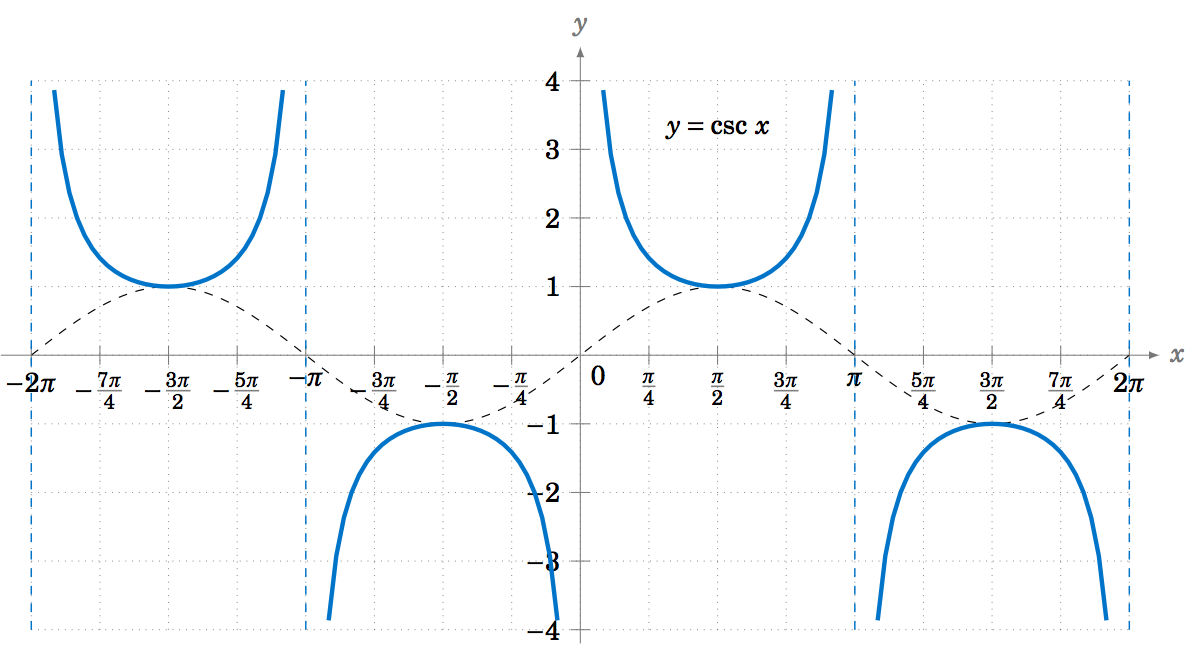
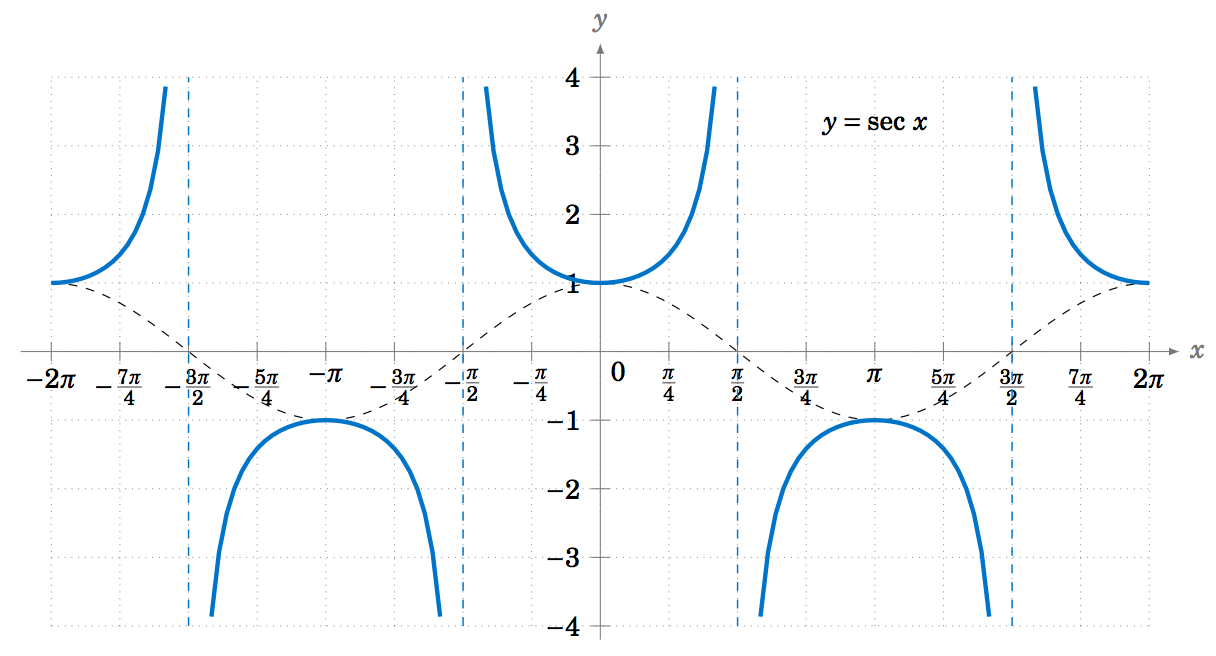
Asimismo, la Figura 5.1.8 muestra la gráfica de$y=\sec\;x $, con la gráfica de$y=\cos\;x $ (la curva discontinua) para referencia. Anote las asíntotas verticales en$x=\pm\,\frac{\pi}{2} $,$\pm\,\frac{3\pi}{2} $. Observe también que la gráfica es solo la gráfica de la función cosecante desplazada hacia la izquierda por$\frac{\pi}{2} $ radianes.

alt — Figura 5.1.8 Gráfico de$y = \sec x$

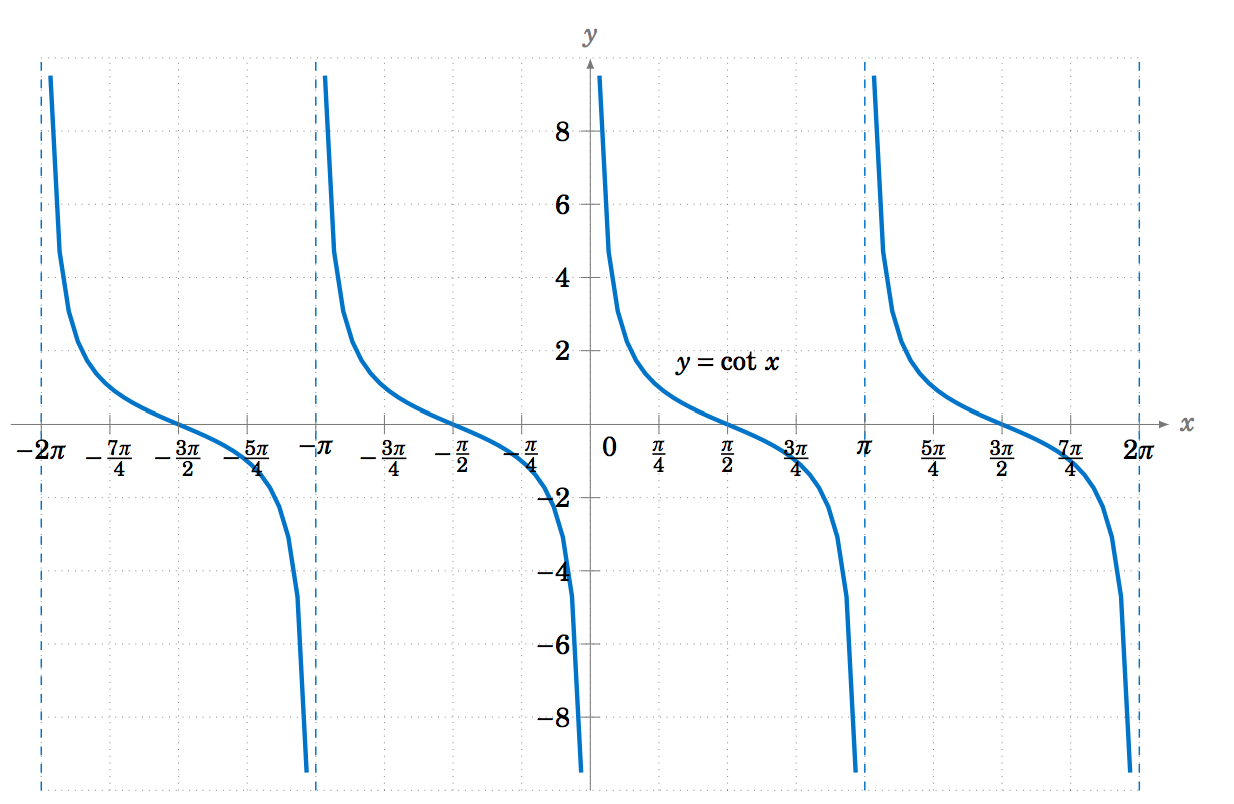
La gráfica de también$y=\cot\;x $ se puede determinar mediante el uso de$\cot\;x = \frac{1}{\tan\;x} $. Alternativamente, podemos usar la relación$\cot\;x = -\tan\;(x+90^\circ) $ de la Sección 1.5, de manera que la gráfica de la función cotangente sea solo la gráfica de la función tangente desplazada hacia la izquierda por$\frac{\pi}{2}$ radianes y luego reflejada alrededor del$x$ eje -como en la Figura 5.1.9:

alt — Figura 5.1.9 Gráfico de$y = \cot x$

Ejemplo$\PageIndex{1}$

Dibuja la gráfica de$y=-\sin\;x $ para$0 \le x \le 2\pi $.

Solución:

Multiplicar una función por$-1 $ solo refleja su gráfica alrededor del$x$ eje -eje. Por lo tanto, reflejar la gráfica de$y=\sin\;x $ alrededor del$x$ eje -nos da la gráfica de$y=-\sin\;x$:

$alt$

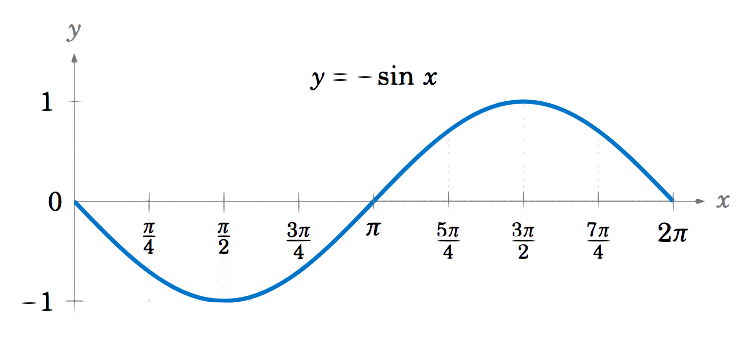
\ noindent Tenga en cuenta que esta gráfica es la misma que las gráficas de$y=\sin\;(x \pm \pi) $ y$y=\cos\;(x+\frac{\pi}{2}) $.

Vale la pena recordar las formas generales de las gráficas de las seis funciones trigonométricas, especialmente para seno, coseno y tangente. En particular, las gráficas de las funciones seno y coseno se denominan curvas sinusoidales. Muchos fenómenos en la naturaleza exhiben un comportamiento sinusoidal, por lo que es importante reconocer la forma general.

Ejemplo$\PageIndex{2}$

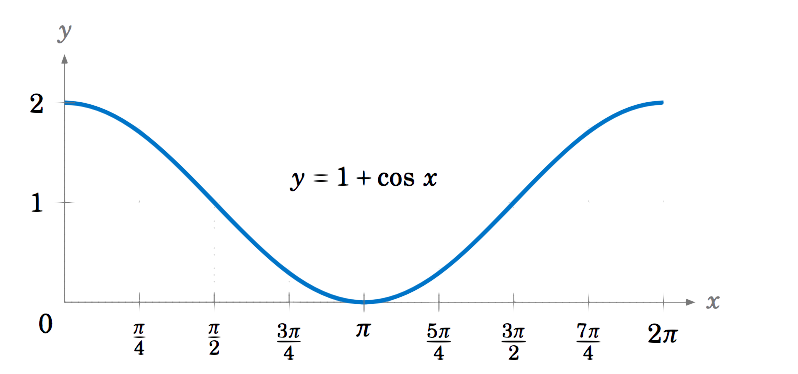
Dibuja la gráfica de$y=1+\cos\;x $ para$0 \le x \le 2\pi $.

Solución

Agregar una constante a una función simplemente mueve su gráfica hacia arriba o hacia abajo en esa cantidad, dependiendo de si la constante es positiva o negativa, respectivamente. Así que$1 $ sumar a$\cos\;x $ mueve la gráfica de$y=\cos\;x $ hacia arriba por$1 $, dándonos la gráfica de$y=1+\cos\;x$:

$alt$

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Solución