5.2: Propiedades de las Gráficas de Funciones Trigonométricas
- Page ID
- 113477
Vimos en la Sección 5.1 cómo las gráficas de las funciones trigonométricas repiten cada\(2\pi \) radianes. En esta sección discutiremos esta y otras propiedades de las gráficas, especialmente para las funciones sinusoidales (seno y coseno).
Primero, recordemos que el dominio de una función\(f(x) \) es el conjunto de todos los números\(x \) para los que se define la función. Por ejemplo, el dominio de\(f(x) = \sin\;x \) es el conjunto de todos los números reales, mientras que el dominio de\(f(x) = \tan\;x \) es el conjunto de todos los números reales excepto\(x=\pm\,\frac{\pi}{2} \),\(\pm\,\frac{3\pi}{2} \),\(\pm\,\frac{5\pi}{2} \),\(... \). El rango de una función\(f(x) \) es el conjunto de todos los valores que\(f(x) \) pueden hacerse cargo de su dominio. Por ejemplo, el rango de\(f(x)=\sin\;x \) es el conjunto de todos los números reales entre\(-1 \) y\(1 \) (es decir, el intervalo\([-1,1]\)), mientras que el rango de\(f(x) = \tan\;x \) es el conjunto de todos los números reales, como podemos ver en sus gráficas.
Una función\(f(x) \) es periódica si existe un número\(p>0 \) tal que\(x+p \) esté en el dominio de\(f(x) \) siempre que\(x \) sea, y si se mantiene la siguiente relación:
\[\label{eqn:periodic} f(x+p) ~=~ f(x) \quad\text{for all \(x\)} \]
Podría haber muchos números\(p \) que satisfagan los requisitos anteriores. Si hay un número menor\(p \), entonces llamamos a ese número el periodo de la función\(f(x) \).
Las funciones\(\sin\;x \),\(\cos\;x \),\(\csc\;x \), y\(\sec\;x \) todas tienen el mismo periodo:\(2\pi\) radianes. Vimos en la Sección 5.1 que las gráficas de\(y=\tan\;x \) y\(y=\cot\;x \) repiten cada\(2\pi \) radianes pero también repiten cada\(\pi \) radianes. Así, las funciones\(\tan\;x \) y\(\cot\;x \) tienen un periodo de\(\pi \) radianes.
¿Cuál es el periodo de\(f(x)=\sin\;2x\,\)?
Solución
La gráfica de\(y=\sin\;2x \) se muestra en la Figura\(\PageIndex{1}\), junto con la gráfica de\(y=\sin\;x \) para comparación, a lo largo del intervalo\([0,2\pi] \). Tenga en cuenta que\(\sin\;2x \) ``va el doble de rápido” que\(\sin\;x \).
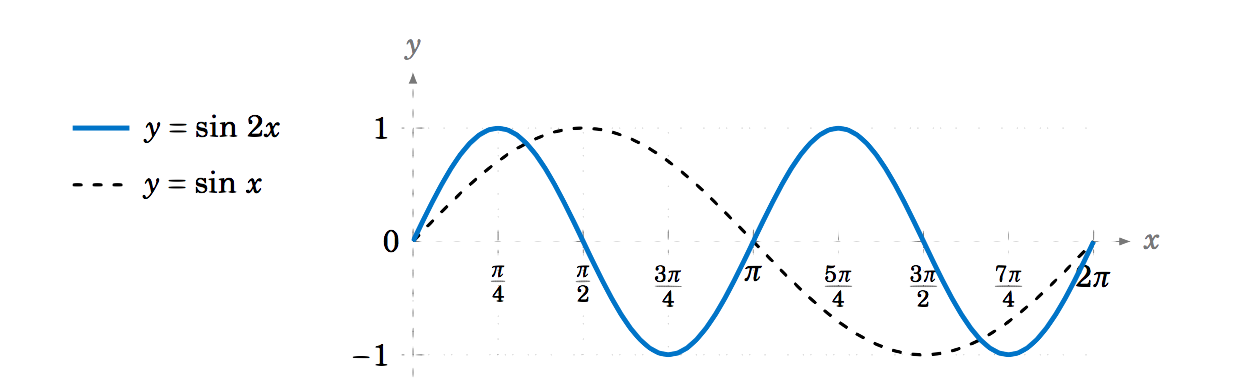
Por ejemplo, para\(x \) de\(0 \) a\(\frac{\pi}{2} \),\(\sin\;x \) va de\(0 \) a\(1 \), pero\(\sin\;2x\) es capaz de pasar de\(0 \) a\(1 \) más rápido, poco más allá del intervalo\([0,\frac{\pi}{4}] \). Si bien\(\sin\;x \) toma un\(2\pi \) radianes completo para pasar por un ciclo completo (la mayor parte de la gráfica que no se repite),\(\sin\;2x \) pasa por un ciclo completo en apenas\(\pi \) radianes. Entonces el periodo de\(\sin\;2x \) es\(\pi \) radianes.
El ejemplo anterior hizo uso de la gráfica de\(\sin\;2x \), pero el periodo se puede encontrar analíticamente. Ya que\(\sin\;x \) tiene periodo\(2\pi \), eso lo sabemos\(\sin\;(x+2\pi) = \sin\;x \) para todos\(x \). Ya que\(2x\) es un número para todos\(x \), esto significa en particular eso\(\sin\;(2x+2\pi) = \sin\;2x \) para todos\(x \). Ahora defina\(f(x)=\sin\;2x \). Entonces
\ [\ nonumber\ begin {align*}
f (x+\ pi) ~&=~\ sin\; 2\, (x+\ pi)\\\ nonumber
&=~\ sin\ ;( 2x+2\ pi)\\ nonumber
&=~\ sin\; 2x\ quad\ text {(como mostramos anteriormente)}\\ nonumber
&=~ f (x)
\ end {align*}\ nonumber\]
para todos\(x \), por lo que el periodo\(p \) de\(\sin\;2x \) es como\(\pi \) mucho, por nuestra definición de periodo. Tenemos que demostrar que no\(p>0 \) puede ser menor que\(\pi \). Para ello, usaremos una prueba por contradicción. Es decir, asumir eso\(0<p<\pi \), luego mostrar que esto lleva a alguna contradicción, y por lo tanto no puede ser cierto. Entonces supongamos\(0<p<\pi \). Entonces\(0<2p<2\pi \), y por lo tanto
\ [\ nonumber\ begin {align*}
\ sin\; 2x ~&=~ f (x)\\\ nonumber
&=~ f (x+p)\ quad\ text {(ya que\(p \) es el periodo de\(f(x)\))}\\\ nonumber
&=~\ sin\; 2 (x+p)\\\ nonumber
&=~\ sin\ ;( 2x+2p)
\ end {alinear*}\ nonumber\]
para todos\(x \). Dado que cualquier número se\(u \) puede escribir como\(2x \) para algunos\(x \) (es decir\(u = 2(u/2)\)), esto significa que\(\sin\;u = \sin\;(u+2p) \) para todos los números reales\(u \), y de ahí el periodo de\(\sin\;x \) es como más\(2p \). Esto es una contradicción. ¿Por qué? Porque el periodo de\(\sin\;x \) es\(2\pi > 2p \). De ahí que el periodo\(p \) de no\(\sin\;2x \) pueda ser menor que\(\pi \), por lo que el periodo debe ser igual\(\pi \).
Lo anterior puede parecer mucho trabajo para probar algo que era visualmente obvio a partir de la gráfica (e intuitivamente obvio por la idea de “el doble de rápido”). Por suerte, no necesitamos pasar por todo ese trabajo para cada función, ya que un argumento similar funciona cuando\(\sin\;2x \) es reemplazado por\(\sin\;\omega x \) para cualquier número real positivo\(\omega\): en lugar de dividir\(2\pi \) por\(2 \) para obtener el periodo, dividir por\(\omega \). Y el argumento funciona también para las otras funciones trigonométricas. Así, obtenemos:
Para cualquier número\(\omega >0\):
\ [\ nonumber\ begin {alignat*} {4}
\ sin\;\ omega x ~~&\ text {tiene periodo} ~~\ frac {2\ pi} {\ omega}
\ qquad\ quad&\ csc\;\ omega x ~~&\ text {tiene periodo} ~~\ frac {2\ pi} {\ omega}\\\ nonumber
\ cos\; omega x ~~&\ texto {tiene periodo} ~~\ frac {2\ pi} {\ omega}
\ qquad\ quad&\ sec\;\ omega x ~~&\ text {tiene periodo} ~~\ frac {2\ pi} {\ omega}\\ nonumber
\ tan\;\ omega x ~~&\ text {tiene periodo} ~~\ frac {\ pi} {\ omega}
\ qquad\ quad&\ cot\;\ omega x ~~&\ text {tiene periodo} ~~\ frac {\ pi} {\ omega}
\ end {alignat*}\ nonumber\]
Si\(\omega < 0 \), entonces use\(\sin\;(-A) = -\sin\;A \) y\(\cos\;(-A) = \cos\;A \) (por ejemplo\(\sin\;(-3x) = -\sin\;3x\)).
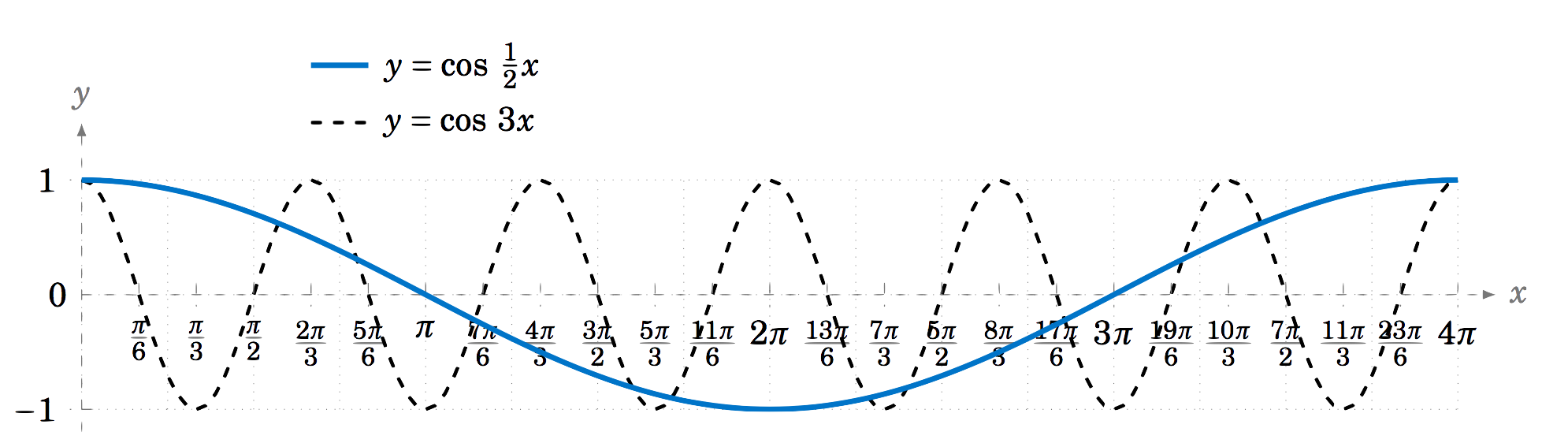
El periodo de\(y=\cos\;3x \) es\(\frac{2\pi}{3} \) y el periodo de\(y=\cos\;\frac{1}{2}x \) es\(4\pi \). Las gráficas de ambas funciones se muestran en la Figura 5.2.2:
Eso lo sabemos\(\;-1 \le \sin\;x \le 1\; \) y\(\;-1 \le \cos\;x \le 1\; \) para todos\(x \). Así, para una constante\(A \ne 0 \),
\ [-|A| ~\ le~ A\,\ sin\; x ~\ le~ |A|\ quad\ texto {y}\ cuádruple
-|A| ~\ le~ A\,\ cos\; x ~\ le~ |A|
\ nonumber\]
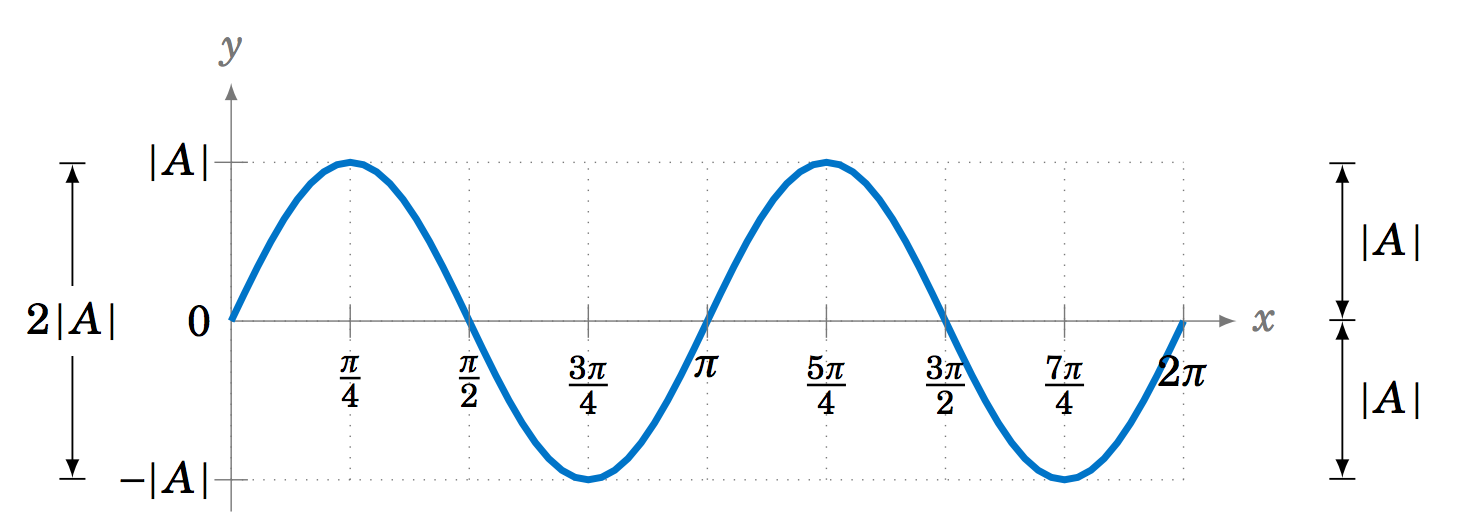
para todos\(x \). En este caso, llamamos a\(|A| \) la amplitud de las funciones\(y=A\,\sin\;x \) y\(y=A\,\cos\;x \). En general, la amplitud de una curva periódica\(f(x)\) es la mitad de la diferencia de los valores más grandes y más pequeños que\(f(x) \) pueden tomar:
\ [\ text {Amplitud de\(f(x)\)} ~=~\ frac {\ text {(máximo de\(f(x)\))} ~-~\ texto {(mínimo de\(f(x)\))}} {2}
\ nonumber\]
Es decir, la amplitud es la distancia desde la parte superior o inferior de la curva hasta la línea horizontal que divide la curva a la mitad, como en la Figura 5.2.3.
No todas las curvas periódicas tienen amplitud. Por ejemplo, no\(\tan\;x \) tiene ni un máximo ni un mínimo, por lo que su amplitud es indefinida. De igual manera\(\cot\;x \)\(\csc\;x \),, y\(\sec\;x \) no tienen una amplitud. Dado que la amplitud involucra distancias verticales, no tiene ningún efecto sobre el periodo de una función, y viceversa.
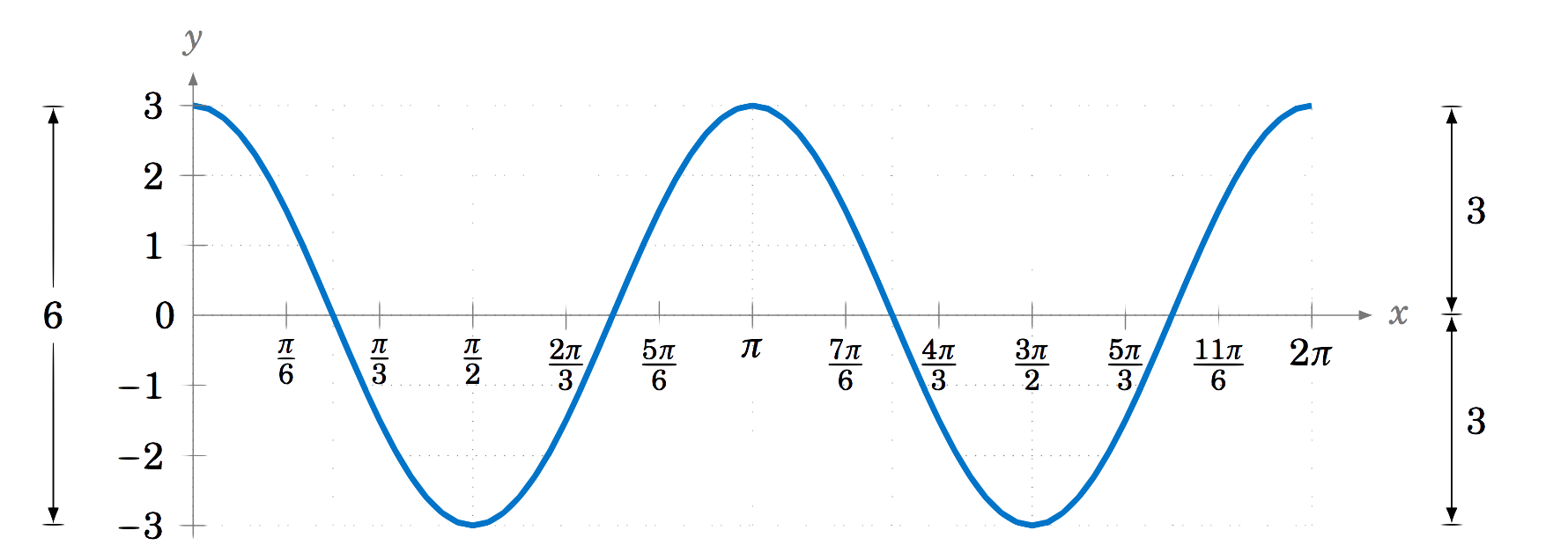
Encuentra la amplitud y periodo de\(y=3\,\cos\;2x \).
Solución
La amplitud es\(|3| = 3 \) y el periodo es\(\frac{2\pi}{2}=\pi \). El gráfico se muestra en la Figura 5.2.4:
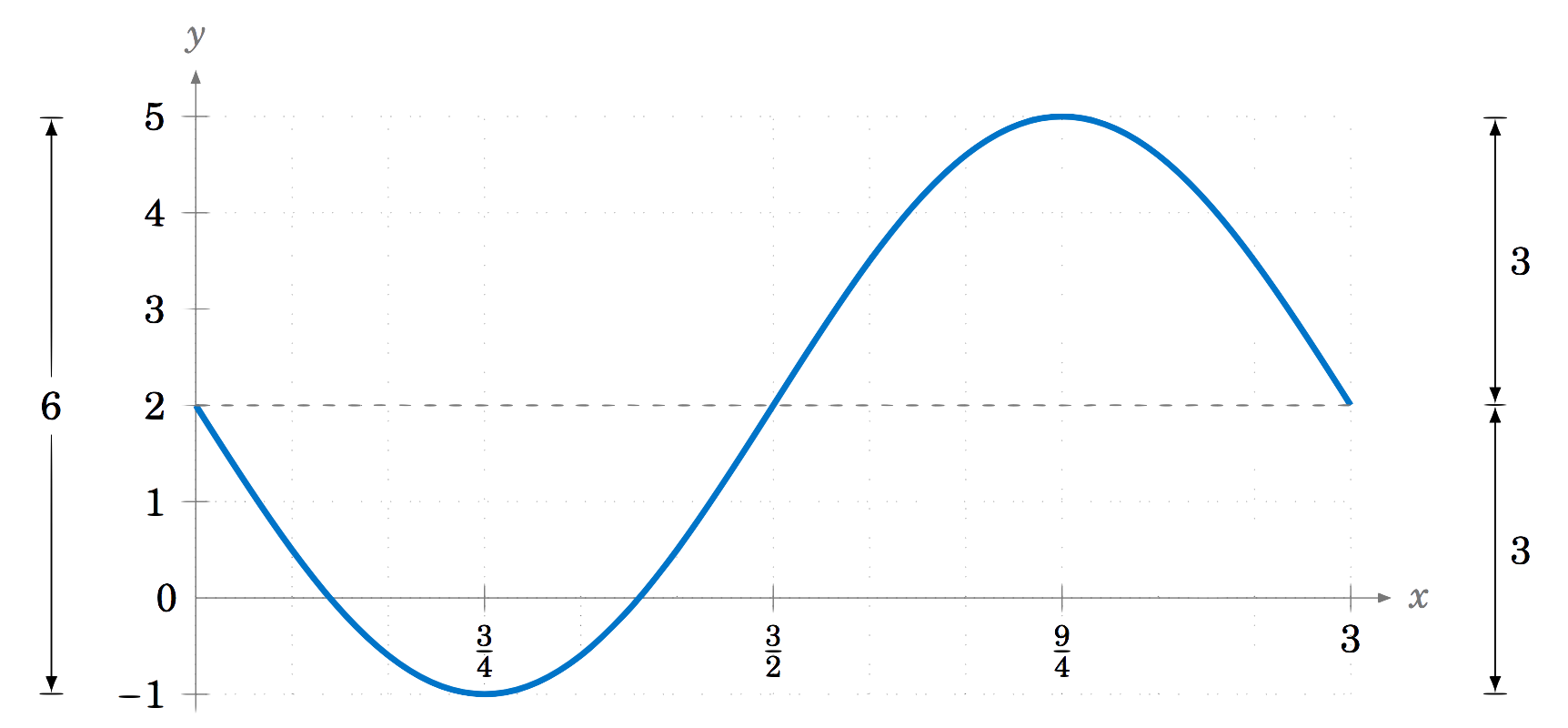
Encuentra la amplitud y periodo de\(y=2 - 3\,\sin\;\frac{2\pi}{3}x \).
Solución
La amplitud de\(-3\,\sin\;\frac{2\pi}{3}x \) es\(|-3| =3 \). Agregar\(2 \) a esa función para obtener la función\(y=2 - 3\,\sin\;\frac{2\pi}{3}x \) no cambia la amplitud, a pesar de que sí cambia el máximo y el mínimo. Simplemente desplaza toda la gráfica hacia arriba por\(2 \). Entonces en este caso, tenemos
\[\nonumber \text{Amplitude} ~=~ \frac{\text{max} ~-~ \text{min}}{2} ~=~ \frac{5 ~-~ (-1)}{2} ~=~ \frac{6}{2} ~=~ 3 ~. \nonumber \]
El periodo es\(\dfrac{2\pi}{\frac{2\pi}{3}}=3 \). El gráfico se muestra en la Figura 5.2.5:
Encuentra la amplitud y periodo de\(y=2\,\sin\;( x^2 ) \).
Solución
Esta no es una función periódica, ya que el ángulo del que estamos tomando el seno,\(x^2 \), no es una función lineal de\(x \), es decir, no es de la forma\(ax+b \) para algunas constantes\(a \) y\(b \). Recordemos cómo argumentamos que\(\sin\;2x \) era ``dos veces más rápido” que\(\sin\;x \), de manera que su periodo fue\(\pi \) en vez de\(2\pi \). ¿Podemos decir que\(\sin\;( x^2 ) \) son algunos tiempos constantes tan rápidos como\(\sin\;x\,\)? No. De hecho, vemos que la “velocidad” de la curva sigue aumentando a medida\(x \) que aumenta, ya que\(x^2 \) crece a una tasa variable, no a una tasa constante. Esto se puede ver en la gráfica de\(y=2\,\sin\;( x^2 ) \), que se muestra en la Figura 5.2.6:
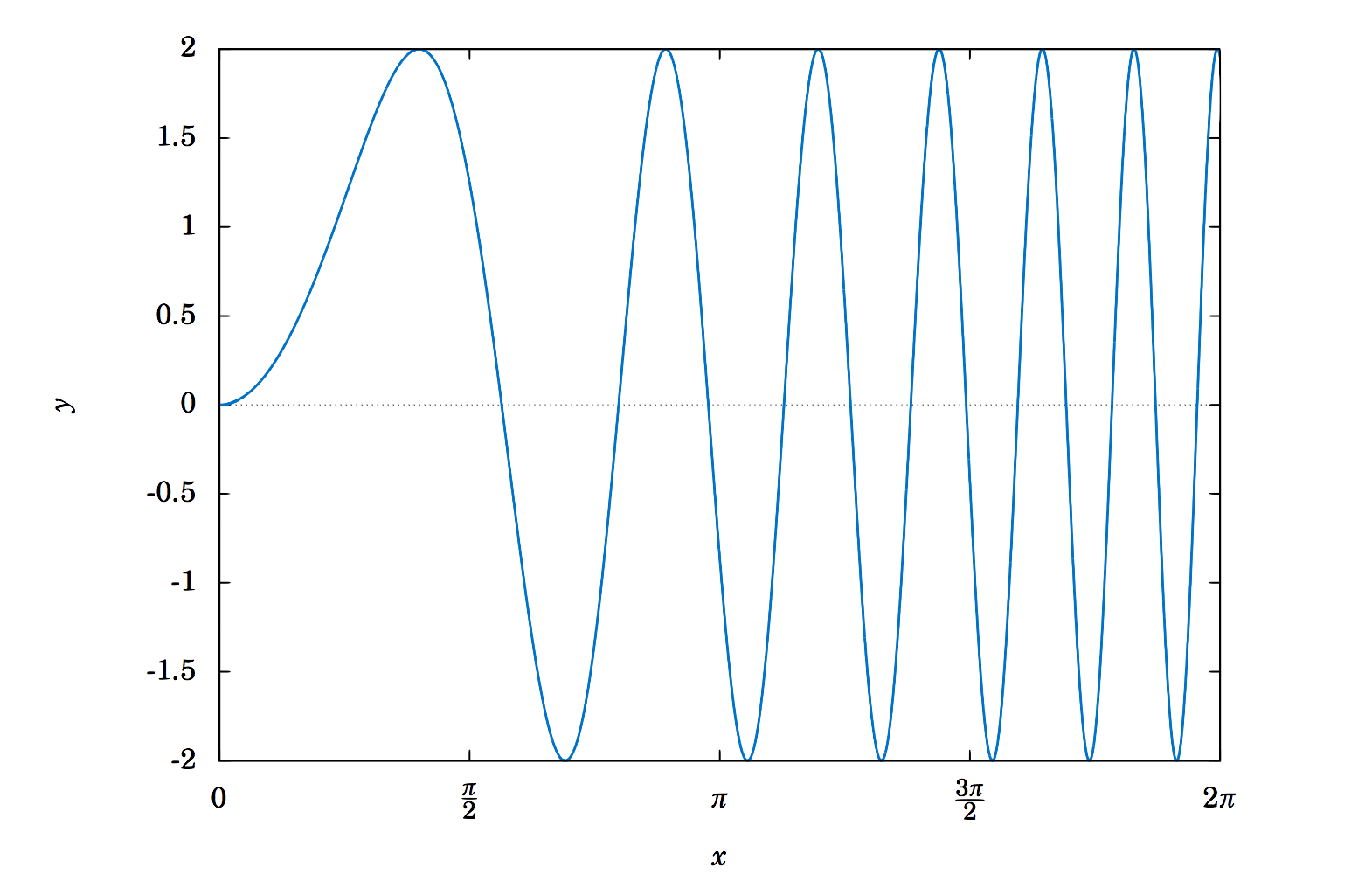
Observe cómo la curva “acelera” a medida que\(x \) se hace más grande, haciendo que las “ondas” sean cada vez más estrechas. Por lo tanto, no\(y=2\,\sin\;( x^2 ) \) tiene periodo. A pesar de ello, parece que la función sí tiene una amplitud, a saber\(2 \). Para ver por qué, tenga en cuenta que ya que\(|\sin\;\theta | \le 1 \) para todos\(\theta \), tenemos
\[| 2\,\sin\;( x^2 )| ~=~ |2| \;\cdot\; |\sin\;( x^2 )| ~\le~ 2 \;\cdot\; 1 ~=~ 2 ~. \nonumber \]
En los ejercicios se le pedirá encontrar valores de\(x \) tales que\(2\,\sin\;( x^2 ) \) alcancen el valor máximo\(2 \) y el valor mínimo\(-2 \). Así, la amplitud es efectivamente\(2 \).
Nota: Esta curva sigue siendo sinusoidal a pesar de no ser periódica, ya que la forma general sigue siendo la de una “onda sinusoidal”, aunque con ciclos variables.
Hasta el momento en nuestros ejemplos hemos podido determinar las amplitudes de las curvas sinusoidales con bastante facilidad. Este no siempre será el caso.
Encuentra la amplitud y periodo de\(y=3\,\sin\;x + 4\,\cos\;x \).
Solución
Esto a veces se denomina curva sinusoidal combinada, ya que es la suma de dos de tales curvas. El periodo sigue siendo sencillo de determinar: ya que\(\sin\;x \) y\(\cos\;x \) cada repetición cada\(2\pi \) radianes, entonces también lo hace la combinación\(3\,\sin\;x + 4\,\cos\;x \). Así,\(y=3\,\sin\;x + 4\,\cos\;x \) tiene periodo\(2\pi \). Esto lo podemos ver en la gráfica, que se muestra en la Figura 5.2.7:
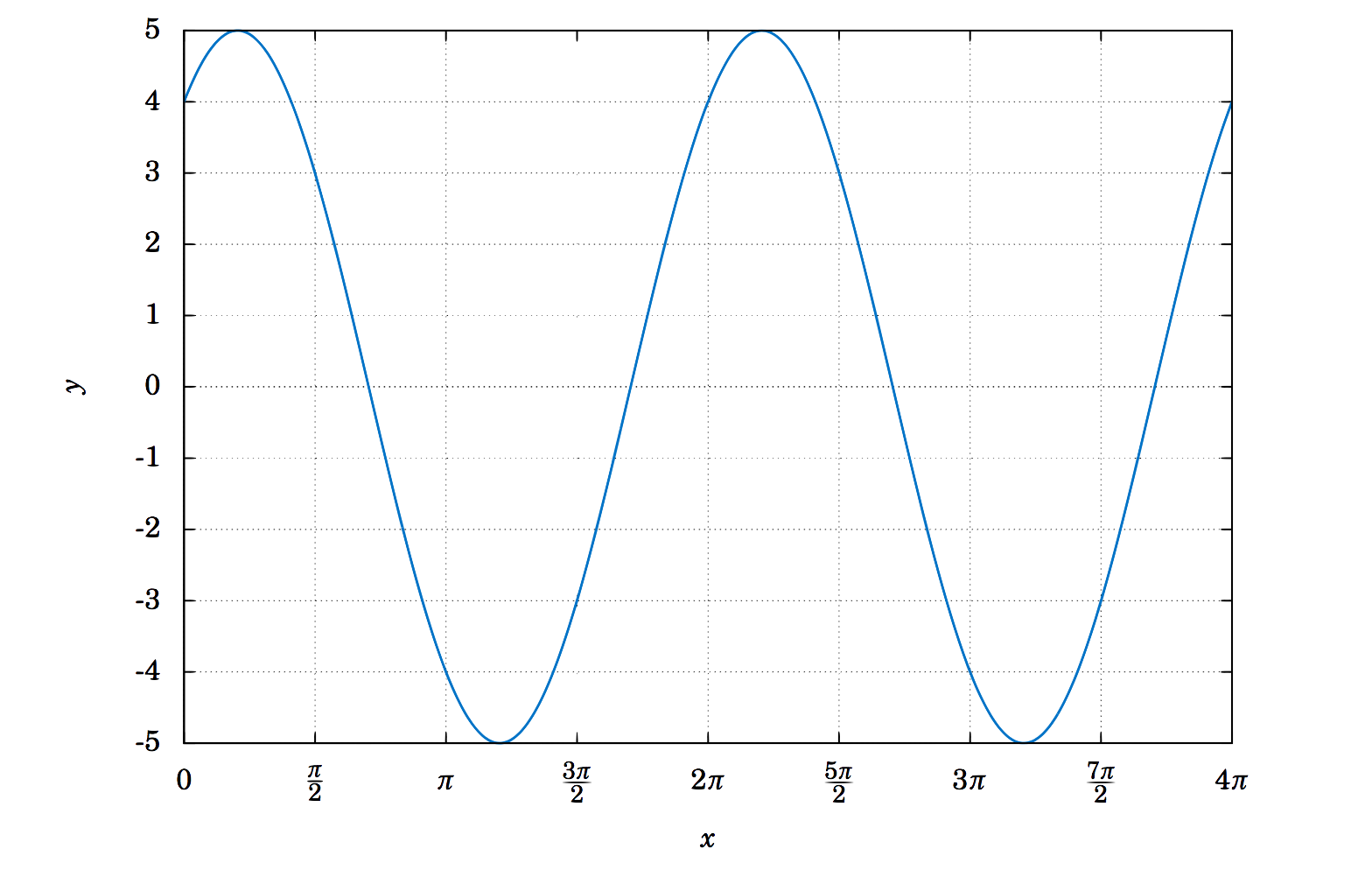
El gráfico sugiere que la amplitud es\(5 \), lo que puede no ser inmediatamente obvio con solo mirar cómo se define la función. De hecho, la definición\(y=3\,\sin\;x + 4\,\cos\;x \) puede tentarte a pensar que la amplitud es\(7 \), ya que la mayor que\(3\,\sin\;x \) podría ser es\(3 \) y la mayor que\(4\,\cos\;x \) podría ser es\(4 \), por lo que la mayor que podría ser su suma es\(3+4=7 \). Sin embargo, nunca\(3\,\sin\;x \) se puede igualar\(3 \) por lo mismo\(x \) que hace\(4\,\cos\;x \) igual a\(4 \) (¿por qué?).
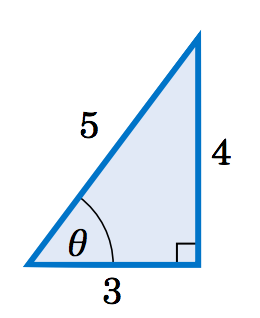
Existe una técnica útil (que discutiremos más adelante en el Capítulo 6) para mostrar que la amplitud de\(y=3\,\sin\;x + 4\,\cos\;x \) es\(5 \). Dejar\(\theta \) ser el ángulo que se muestra en el
triángulo rectángulo en la Figura 5.2.8. Entonces\(\cos\;\theta = \frac{3}{5} \) y\(\sin\;\theta = \frac{4}{5} \). Podemos usar esto de la siguiente manera:
\ [\ nonumber\ begin {align*}
y ~&=~ 3\,\ sin\; x ~+~ 4\,\ cos\; x\\ nonumber
&=~ 5\,\ izquierda (\ tfrac {3} {5}\,\ sin\; x ~+~\ tfrac {4} {5}\,\ cos\; x\ derecha)\\ nonumber
&=~ 5\, (\ cos\;\ theta\;\ sin\; x ~+~\ sin\;\ theta\;\ cos\; x)\\\ nonumber
&=~ 5\,\ sin\; (x+\ theta)\ quad\ text {(por la fórmula de suma sinusoidal)}
\ end {align*}\ nonumber\]
Así,\(|y| = |5\,\sin\;(x+\theta)| = |5|\,\cdot\,|\sin\;(x+\theta)| \le (5)(1) = 5 \), así la amplitud de\(y=3\,\sin\;x + 4\,\cos\;x \) es\(5 \).
En general, una combinación de senos y cosenos tendrá un periodo igual al múltiplo común más bajo de los periodos de los senos y cosenos que se están agregando. En el Ejemplo 5.9,\(\sin\;x \) y\(\cos\;x \) cada uno tiene punto\(2\pi \), por lo que el múltiplo común más bajo (que siempre es un múltiplo entero) es\(1 \,\cdot\, 2\pi = 2\pi \).
Encuentra el periodo de\(y=\cos\;6x + \sin\;4x \).
Solución
El periodo de\(\cos\;6x \) es\(\frac{2\pi}{6} = \frac{\pi}{3} \), y el periodo de\(\sin\;4x \) es\(\frac{2\pi}{4} = \frac{\pi}{2} \). El múltiplo común más bajo de\(\frac{\pi}{3} \) y\(\frac{\pi}{2} \) es\(\pi\):
\ [\ nonumber\ begin {alignat*} {4}
1\;\ cdot\;\ tfrac {\ pi} {3} ~&=~\ tfrac {\ pi} {3}\ quad\ cuádruple\ cuádruple
&1\; &\ cdot\;\ tfrac {\ pi} {2} ~&=~\ tfrac {\ pi}\ nonumber
2\;\ cdot\;\ tfrac {\ pi} {3} ~&=~\ tfrac {2\ pi} {3}\ quad\ quad\ quad
&2\; & \ cdot\;\ tfrac {\ pi} {2} ~&=~\ pi\\ nonúmero
3\;\ cdot\;\ tfrac {\ pi} {3} ~&=~\ pi\ quad\ quad\ quad & {} & {}\\ nonumber
\ end {alignat*}\ nonumber\]
Así, el periodo de\(y=\cos\;6x + \sin\;4x \) es\(\pi \). Esto lo podemos ver en su gráfica en la Figura 5.2.9:
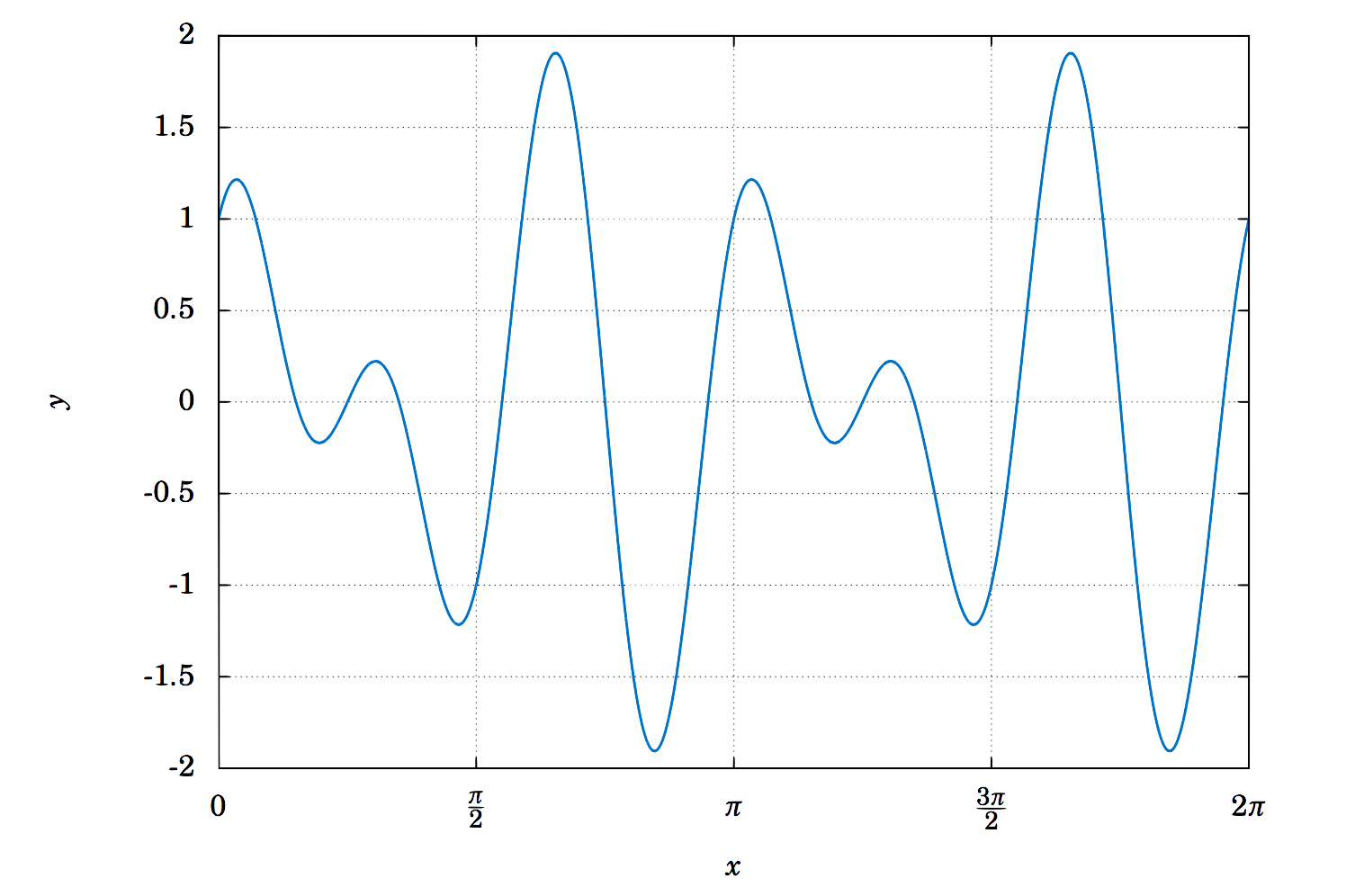
¿Qué pasa con la amplitud? Desafortunadamente no podemos usar la técnica del Ejemplo 5.9, ya que no estamos tomando el coseno y el seno del mismo ángulo; estamos tomando el coseno de\(6x \) sino el seno de\(4x \). En este caso, se desprende de la gráfica que el máximo está cerca\(2 \) y el mínimo está cerca\(-2 \). En el Capítulo 6, describiremos cómo usar un programa de cómputo numérico para mostrar que el máximo y el mínimo son\(\pm\,1.90596111871578 \), respectivamente (precisos hasta dentro\(\approx 2.2204 \times 10^{-16}\)). De ahí que la amplitud sea\(1.90596111871578 \).
Generalizando Ejemplo 5.9, una expresión de la forma\(a\,\sin\;\omega x \;+\; b\,\cos\;\omega x \) es equivalente a\(\sqrt{a^2 + b^2}\;\sin\;(x+\theta) \), donde\(\theta \) es un ángulo tal que\(\cos\;\theta = \frac{a}{\sqrt{a^2 + b^2}} \) y\(\sin\;\theta = \frac{b}{\sqrt{a^2 + b^2}} \). Así\(y=a\,\sin\;\omega x \;+\; b\,\cos\;\omega x \) tendrá amplitud\(\sqrt{a^2 + b^2} \). Tenga en cuenta que este método solo funciona cuando el ángulo\(\omega x \) es el mismo tanto en términos de seno como coseno.
Hemos visto como agregar una constante a una función desplaza verticalmente toda la gráfica. Ahora veremos cómo desplazar horizontalmente toda la gráfica de una curva periódica.
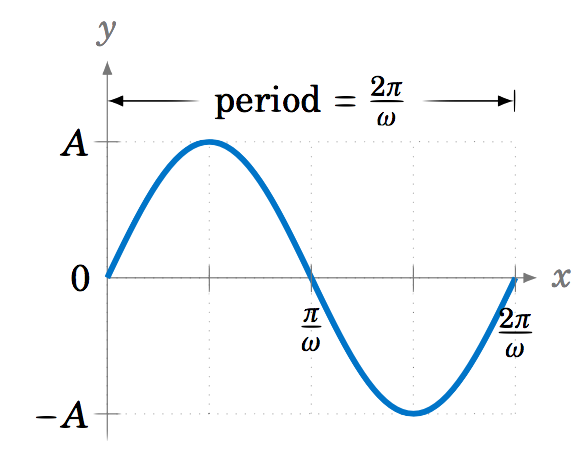
Considerar una función de la forma\(y=A\,\sin\;\omega x \), donde\(A \) y\(\omega \) son constantes distintas de cero. Por simplicidad vamos a suponer que\(A >0 \) y\(\omega > 0 \) (en general cualquiera de ellos podría ser negativo). Entonces la amplitud es\(A \) y el periodo es\(\frac{2\pi}{\omega} \). La gráfica se muestra en la Figura 5.2.10.
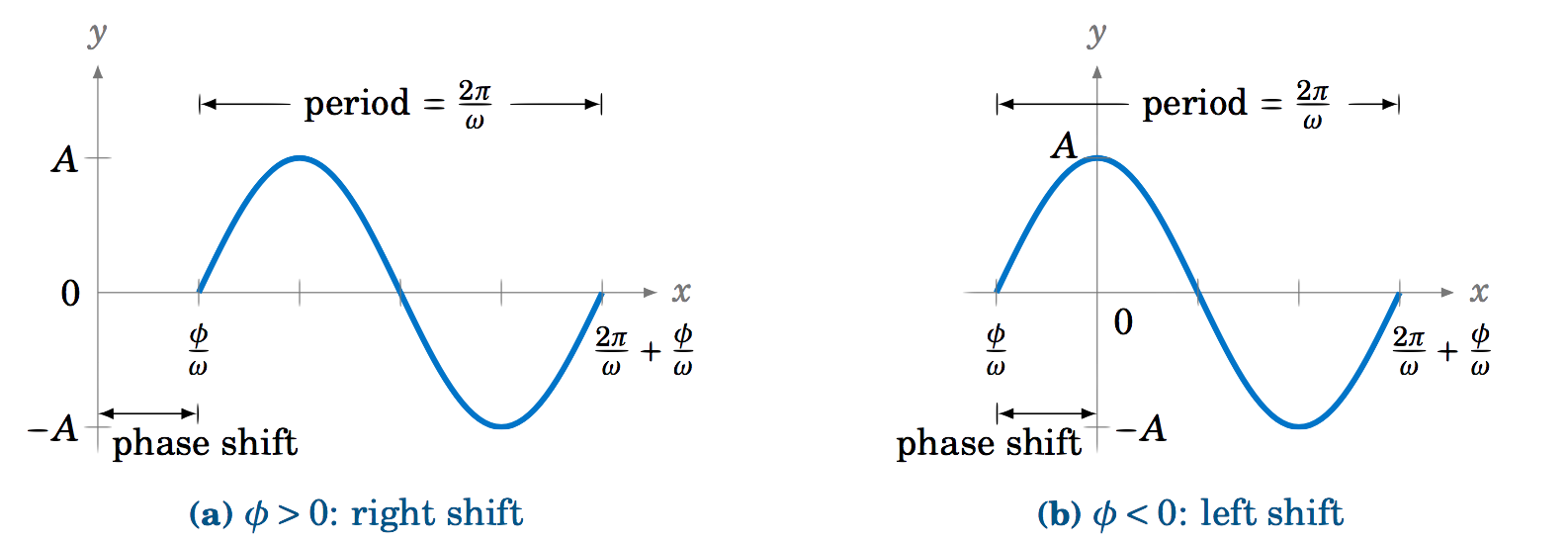
Ahora consideremos la función\(y=A\,\sin\;(\omega x - \phi) \), donde\(\phi \) hay alguna constante. La amplitud es todavía\(A \), y el periodo sigue siendo\(\frac{2\pi}{\omega} \), ya que\(\omega x - \phi \) es una función lineal de\(x \). También, sabemos que la función sinusoidal pasa por todo un ciclo cuando su ángulo va de\(0 \) a\(2\pi \). Aquí, estamos tomando el seno del ángulo\(\omega x - \phi \). Entonces como\(\omega x - \phi \) va de\(0 \) a\(2\pi \), se\(y=A\,\sin\;(\omega x - \phi) \) trazará un ciclo completo de la función. Ese ciclo comienza cuando
\[\nonumber \omega x - \phi ~=~ 0 \quad \Rightarrow\quad x ~=~ \frac{\phi}{\omega} \nonumber \]
y termina cuando
\[\nonumber \omega x - \phi ~=~ 2\pi \quad \Rightarrow\quad x ~=~ \frac{2\pi}{\omega}\;+\;\frac{\phi}{\omega}~. \nonumber \]
Así, la gráfica de\(y=A\,\sin\;(\omega x - \phi) \) es solo la gráfica de\(y=A\,\sin\;\omega x\) desplazada horizontalmente por\(\frac{\phi}{\omega} \), como en la Figura 5.2.11. La gráfica se desplaza a la derecha cuando\(\phi >0 \), y a la izquierda cuando\(\phi <0 \). La cantidad\(\frac{\phi}{\omega} \) del desplazamiento se denomina desplazamiento de fase de la gráfica.
El desplazamiento de fase se define de manera similar para las otras funciones trigonométricas.
Encuentra la amplitud, periodo, y desplazamiento de fase de\(y=3\,\cos\;(2x - \pi) \).
Solución
La amplitud es\(3 \), el periodo es\(\frac{2\pi}{2} = \pi \), y el desplazamiento de fase es\(\frac{\pi}{2} \). El gráfico se muestra en la Figura 5.2.12:
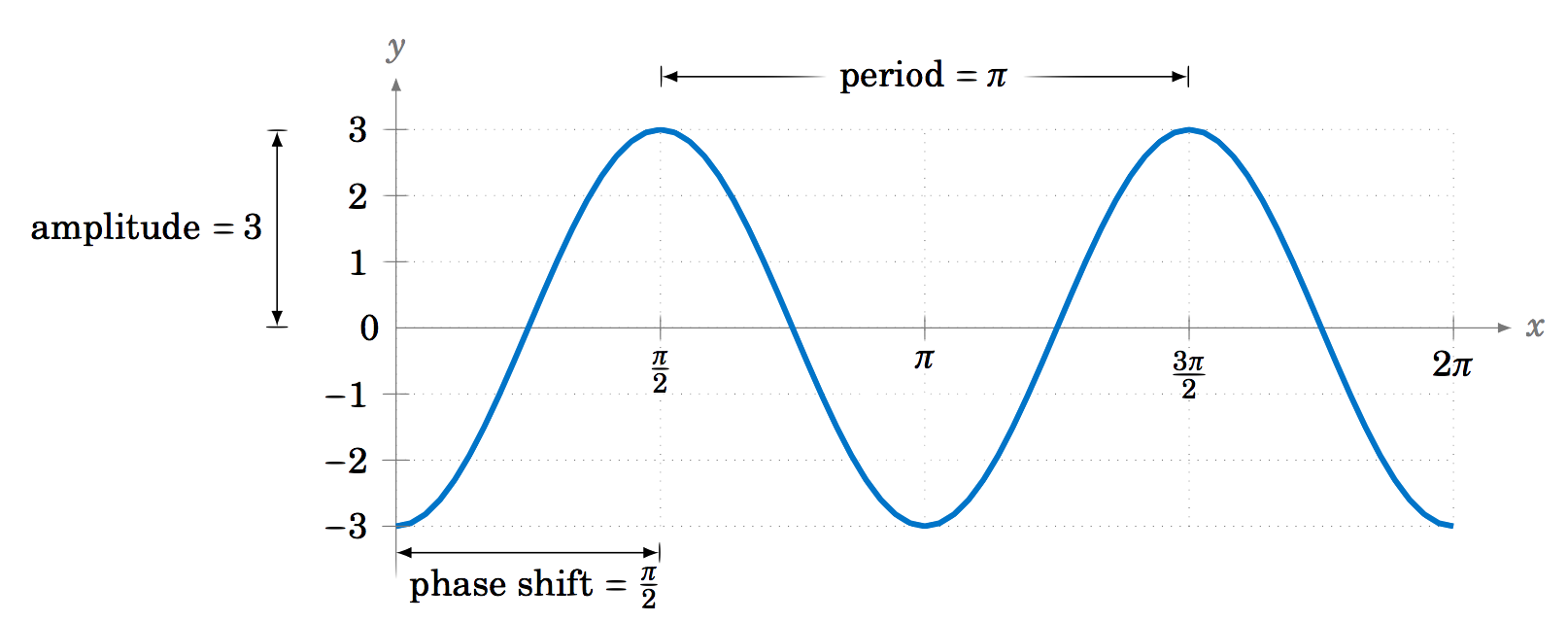
Observe que la gráfica es la misma que la gráfica de\(y=3\,\cos\;2x \) desplazada a la derecha por\(\frac{\pi}{2} \), la cantidad del desplazamiento de fase.
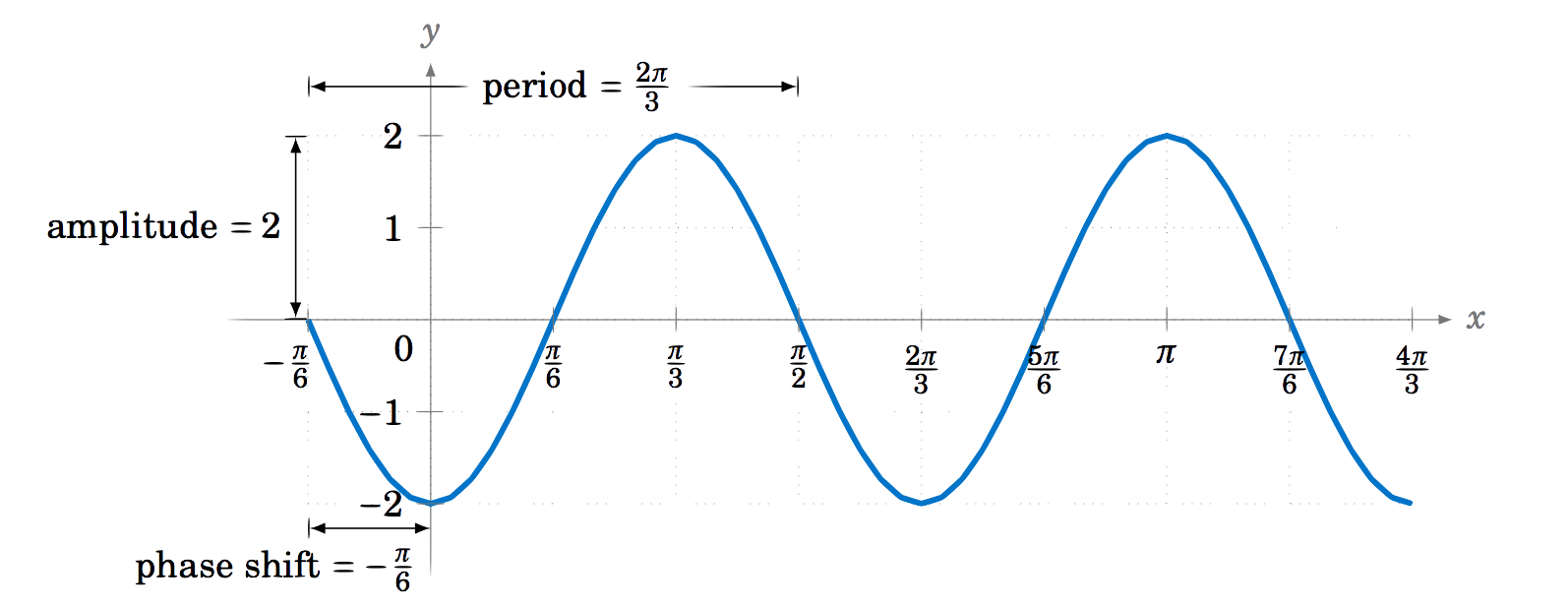
Encuentra la amplitud, periodo, y desplazamiento de fase de\(y=-2\,\sin\;\left(3x + \frac{\pi}{2}\right) \).
Solución
La amplitud es\(2 \), el periodo es\(\frac{2\pi}{3} \), y el desplazamiento de fase es\(\frac{-\frac{\pi}{2}}{3} = -\frac{\pi}{6} \). Observe el signo negativo en el desplazamiento de fase, ya que\(3x+\pi=3x-(-\pi) \) está en la forma\(\omega x - \phi \). El gráfico se muestra en la Figura 5.2.13:
En ingeniería se dice que dos funciones periódicas con el mismo periodo están desfasadas si sus desplazamientos de fase difieren. Por ejemplo,\(\sin\;\left( x - \frac{\pi}{6} \right) \) y\(\sin\;x \) serían\(\frac{\pi}{6} \) radianes (o\(30^\circ\)) fuera de fase, y se\(\sin\;x \) diría que se rezaga\(\sin\;\left( x - \frac{\pi}{6} \right) \) por\(\frac{\pi}{6} \) radianes, mientras que\(\sin\;\left( x - \frac{\pi}{6} \right) \) lleva\(\ sin\; x\) por\(\frac{\pi}{6} \) radianes. Las funciones periódicas con el mismo periodo y el mismo desplazamiento de fase están en fase.
El siguiente es un resumen de las propiedades de las gráficas trigonométricas:
Para cualquier constante\(A \ne 0 \),\(\omega \ne 0 \), y\(\phi\):
\ [\ nonumber\ begin {align*}
y = A\,\ sin\ ;(\ omega x -\ phi) ~~~&\ text {tiene amplitud\(|A| \)\(\tfrac{2\pi}{\omega} \), periodo y desplazamiento de
fase\(\tfrac{\phi}{\omega}\)}\\\ nonumber
y = A\,\ cos\ ;(\ omega x -\ phi) ~~~&\ text {tiene amplitud\(|A| \), periodo\(\tfrac{2\pi}{\omega} \), y
desplazamiento de fase\(\tfrac{\phi}{\omega}\)}\\\ nonúmero
y = A\,\ tan\ ;(\ omega x -\ phi) ~~&\ text {tiene amplitud\(\tfrac{\pi}{\omega} \), periodo y desplazamiento de
fase indefinidos\(\tfrac{\phi}{\omega}\)}\\\ nonumber
y = A\,\ csc\ ;(\ omega x -\ phi) ~~~&\ text {tiene amplitud indefinida, periodo\(\tfrac{2\pi}{\omega} \), y
desplazamiento de fase\(\tfrac{\phi}{\omega}\)}\\\ nonúmero
y = A\,\ sec\ ;(\ omega x -\ phi) ~~~&\ text {tiene amplitud\(\tfrac{2\pi}{\omega} \), periodo y desplazamiento de
fase indefinidos\(\tfrac{\phi}{\omega}\)}\\\ nonumber
y = A\,\ cot\ ;(\ omega x -\ phi) ~~~&\ text {tiene amplitud indefinida, periodo \(\tfrac{\pi}{\omega} \), y desplazamiento de
fase\(\tfrac{\phi}{\omega}\)}
\ end {align*}\ nonumber\]


