2.6: Desigualdades

Última actualización
Guardar como PDF

Page ID: 111615

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En el Capítulo 1, introdujimos los números naturales$\mathbb{N}=\{1,2,3, \ldots\}$, los números$\mathbb{W}=\{0,1,2,3, \ldots\}$ enteros y los enteros$\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\}$. Posteriormente en el capítulo, introdujimos los números racionales, los números de la forma$p/q$, donde$p$ y$q$ son enteros. Señalamos que tanto los decimales terminantes como los repetidos son números racionales. Cada uno de estos números tiene una posición única en la recta numérica (ver Figura$\PageIndex{1}$).

fig 2.6.1.png — Figura$\PageIndex{1}$: Posicionamiento de números en la recta numérica.

Los números naturales, números enteros y enteros también son números racionales, porque cada uno puede expresarse en la forma$\frac{p}{q}$, donde$p$ y$q$ son enteros. Por ejemplo,$0=\frac{0}{12}$,$4 = \frac{4}{1}$, y$-3=\frac{-12}{4}$. En efecto, los números racionales contienen todos los números que hemos estudiado hasta este momento en el curso. Sin embargo, no todos los números son números racionales. Por ejemplo, considere el número decimal$-3.10110111011110 \ldots$, que ni termina ni repite. El número$\sqrt{2}=1.414213562373095 \ldots$ también equivale a un número decimal que nunca termina y nunca se repite. Se puede hacer una declaración similar sobre el número$\pi=3.141592653589793 \dots$ Cada uno de estos números irracionales (no racionales) también tiene una posición única en la recta numérica (ver Figura$\PageIndex{2}$).

fig 2.6.2.png — Figura$\PageIndex{2}$: Posicionamiento de números en la recta numérica.

Otros dos números irracionales que puedes encontrar en tus estudios matemáticos son$e$ (la constante de Euler), que es aproximadamente igual a$e \approx 2.71828182845904 \ldots$, y$\phi$ (pronunciado “phi”), llamado la proporción áurea, que es igual$\phi= \frac{1+\sqrt{5}}{2}$. El número$e$ surge en aplicaciones que involucran interés compuesto, probabilidad y otras áreas de las matemáticas. El número$\phi$ se utiliza en los mercados financieros y también podría decirse que es la proporción de belleza en el arte y la arquitectura.

Los números reales

Si combinamos todos los números racionales e irracionales en una colección, entonces tenemos un conjunto de números que se llama el conjunto de números reales. El conjunto de números reales se denota con el símbolo$\mathbb{R}$.

Cada punto de la línea numérica está asociado con un número real único. Por el contrario, cada número real está asociado con una posición única en la recta numérica. En lugar de esta correspondencia, la línea numérica suele llamarse línea real.

Ordenar los números reales

Los números reales se ordenan en la línea real de una manera idéntica a como ordenamos los números enteros en la línea numérica en la Sección 1 del Capítulo 1.

Orden en la Línea Real

Supongamos que$a$ y$b$ son números reales posicionados en la línea real como se muestra a continuación.

$fig 2.6.a.png$

Porque$a$ miente a la “izquierda de”$b$, decimos que$a$ es “menor que”$b$, o en símbolos matemáticos,$a<b$. El símbolo de desigualdad$<$ se lee “menos que”.
Como alternativa,$b$ se encuentra a la “derecha de”$a$, por lo que también podemos decir que$b$ es “mayor que”$a$, o en símbolos matemáticos,$b>a$. El símbolo de desigualdad$>$ se lee “mayor que”.

Aquí hay dos símbolos de desigualdad más que usaremos en esta sección.

Menor o igual a

Si queremos decir que$a$ miente a la “izquierda de”$b$, o comparte la misma posición que$b$, entonces decimos que$a$ es “menor o igual a”$b$ y escribimos$a ≤ b$. El símbolo de desigualdad$≤$ se pronuncia “menor o igual a”.

Mayor o igual a

Si queremos decir que$b$ miente al “derecho de”$a$, o comparte la misma posición que$a$, entonces decimos que$b$ es “mayor o igual a”$a$ y escribimos$b≥ a$. El símbolo de desigualdad$≥$ se pronuncia “mayor o igual a”.

Notación de Set-Builder

Los matemáticos utilizan un constructo llamado notación set-builder para describir conjuntos o colecciones de números. La forma general de notación set-builder se ve de la siguiente manera:\[\{x : \text { some statement about } x\} \nonumber \] Por ejemplo, supongamos que queremos describir el conjunto de “todos los números reales que son menores que”$2$. Podríamos usar la siguiente notación:\[A=\{x : x<2\} \nonumber \]

Esto se lee en voz alta de la siguiente manera: “$A$equivale al conjunto de todos los$x$ tales que$x$ es menor que”$2$. Algunos prefieren usar una barra vertical en lugar de dos puntos. \[A=\{x \, | \, x<2\} \nonumber \]En este texto usamos los dos puntos en la notación set-builder, pero no dude en usar la barra vertical en su lugar. Significan lo mismo. Todavía se podría objetar que la notación\[\{x : x<2\} \nonumber \] es un poco vaga. Una objeción podría ser “¿A qué tipo de números$x$ se refiere? ¿Quieres los enteros que son menores de dos o quieres los números reales que son menos de dos?” Como puede ver, se trata de una objeción válida. Una forma de abordar esta objeción es escribir:\[A=\{x \in \mathbb{R} : x<2\} \quad \text { or } \quad A=\{x \in \mathbb{N} : x<2\} \nonumber \] La primera se lee “$A$es el conjunto de todos$x$ en$R$ que son menos de dos”, mientras que la segunda se lee “$A$es el conjunto de todos$x$ en$N$ que son menos de dos”.

Asunción de Set-Builder

En este texto, a menos que exista una referencia específica al conjunto de números deseados, asumiremos que la notación$\{x : x<2\}$ está pidiendo el conjunto de todos los números reales menores que$2$.

En Figura$\PageIndex {3}$, hemos sombreado el conjunto de números reales$\{x : x<2\}$. Porque

higo 2.6.3.png — Figura$\PageIndex{3}$: Sombreando los números a menos de$2$.

“menos que” es lo mismo que decir “izquierda de”, hemos sombreado (en rojo) todos los puntos de la línea real que se encuentran a la izquierda del número dos. Tenga en cuenta que hay un “círculo vacío” en el número dos. El punto que representa al número dos no está sombreado porque solo nos pidieron que sombreáramos los números que son estrictamente menores a dos.

Si bien el sombreado en Figura$\PageIndex{3}$ es perfectamente válido, gran parte de la información proporcionada en Figura$\PageIndex{3}$ es innecesaria (y quizás distrae). Solo necesitamos etiquetar el punto final y sombrear los números reales a la izquierda de dos, como hemos hecho en la construcción de la Figura$\PageIndex{4}$.

fig 2.6.4.png — Figura$\PageIndex{4}$: Solo es necesario etiquetar el punto final.

Por contraste, supongamos en cambio que se nos pide que sombreemos el conjunto de números reales$\{x : x\leq2\}$. Esto significa que debemos sombrear todos los números reales

higo 2.6.5.png — Figura$\PageIndex{5}$: Solo es necesario etiquetar el punto final.

que sean “menores o iguales a$2$” o “a la izquierda e inclusive”$2$. El conjunto resultante se sombrea en la Figura$\PageIndex{5}$.

Obsérvese la diferencia entre Figuras$\PageIndex{4}$ y$\PageIndex{45}$. En Figuras$\PageIndex{4}$ estamos sombreando el conjunto$\{x : x<2\}$, por lo que el número$2$ se deja sin sombra (un punto vacío). En Figuras$\PageIndex{5}$, estamos sombreando el conjunto$\{x : x\leq2\}$, por lo que el número$2$ es sombreado (un punto rellenado).

Ejemplo$\PageIndex{1}$

Sombra el set$\{x : x \geq-3\}$ en la línea real.

Solución

La notación$\{x : x \geq-3\}$ se pronuncia “el conjunto de todos los números reales$x$ tal que$x$ sea mayor o igual a”$-3$. Por lo tanto, necesitamos sombrear el número$-3$ y todos los números reales a la derecha de$-3$.

$Ejemplo 1.png$

Ejercicio$\PageIndex{1}$

Sombra$\{x : x \leq 4\}$ en la línea real.

Contestar: $Ejercicio 1.png$

Ejemplo$\PageIndex{2}$

Utilice la notación set-builder para describir el conjunto de números reales que están sombreados en la línea numérica a continuación.

$Ejemplo 2.png$

Solución

El número no$-1$ está sombreado. Sólo los números a la izquierda de$-1$ están sombreados. Este es el conjunto de todos los números reales$x$ tal que$x$ es “menor que”$-1$. Así, describimos este conjunto con la siguiente notación set-builder:\[\{x : x<-1\} \nonumber \]

Ejercicio$\PageIndex{2}$

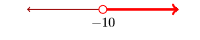
Utilice la notación set-builder para describir el siguiente conjunto de números reales:

$Ejercicio 2.png$

Contestar: $\{x : x>-10\}$

Notación de intervalos

En Ejemplos$\PageIndex{1}$ y$\PageIndex{2}$, utilizamos notación set-builder para describir el conjunto de números reales mayores o iguales a$-3$ y un segundo conjunto de números reales menores que$-1$. Existe otro simbolismo matemático, llamado notación de intervalos, que se puede utilizar para describir estos conjuntos de números reales. Considere el primer conjunto de números de Ejemplo$\PageIndex{1}$,$\{x : x \geq-3\}$.

$fig 2.6.b.png$

Barriendo nuestros ojos “de izquierda a derecha”, usamos$[-3, \infty)$ para describir este conjunto de números reales. Algunos comentarios están en orden:

El soporte en el extremo izquierdo significa que$-3$ está incluido en el conjunto.
A medida que te mueves hacia el extremo derecho de la línea real, los números crecen sin ataduras. De ahí que el$\infty$ símbolo (infinito positivo) se utilice para indicar que estamos incluyendo todos los números reales a la derecha de$-3$. No obstante, en realidad no$\infty$ es un número, así que usamos un paréntesis para indicar que estamos “no incluyendo” este punto ficticio.

El conjunto de números de Ejemplo$\PageIndex {1}$ es$\{x : x<-1\}$.

$fig 2.6.c.png$

Barriendo nuestros ojos “de izquierda a derecha”, se describe con este conjunto de números reales$(-\infty,-1)$. Nuevamente, los comentarios están en orden:

El número no$-1$ está incluido en este conjunto. Para indicar que no está incluido, utilizamos un paréntesis.
A medida que avanzas hacia el extremo izquierdo de la línea real, los números disminuyen sin límite. De ahí que el$-\infty$ símbolo (infinito negativo) se utilice para indicar que estamos incluyendo todos los números reales a la izquierda de$-1$. Nuevamente, no$-\infty$ es un número real, por lo que usamos un paréntesis para indicar que no estamos incluyendo este punto “ficticio”.

Barrer los ojos de “izquierda a derecha”

Si desea asegurarse de que usa correctamente la notación de intervalos, coloque los números en su notación de intervalo en el mismo orden en que se encuentran mientras barre los ojos de “izquierda a derecha” en la línea real.

Un buen resumen de set-builder y notación de intervalo se presenta en Tabla$\PageIndex{1}$ al final de la sección.

Desigualdades equivalentes

Al igual que las ecuaciones, dos desigualdades son equivalentes si tienen los mismos conjuntos de soluciones.

Sumando o restando la misma cantidad de ambos lados de una desigualdad

Dejar$a$ y$b$ ser números reales con\[a < b \nonumber \]
Si$c$ es cualquier número real, entonces\[a + c<b+ c \nonumber \] y Es\[a−c<b−c \nonumber \] decir, sumar o restar la misma cantidad de ambos lados de una desigualdad produce una desigualdad equivalente (no cambia la solución).

Ejemplo$\PageIndex{3}$

Resolver para$x: \quad x-2 ≤ 7$. Esboce la solución en la línea real, luego use el generador de conjuntos y la notación de intervalos para describir su solución.

Solución

Para “deshacer” restar$2$, sumamos$2$ a ambos lados de la desigualdad.

\[\begin{aligned} x-2 &\leq 7 & & \color {Red} \text { Original inequality. } \\ x-2+2 &\leq 7+2 & & \color {Red} \text { Add } 2 \text { to both sides. } \\ x &\leq 9 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Para sombrear los números reales menores o iguales a$9$, sombreamos el número$9$ y todos los números reales a la izquierda de$9$.

$fig 2.6.d.png$

Usando la notación set-builder, la solución es$\{x : x \leq 9\}$. Usando la notación de intervalos, la solución es$(-\infty, 9]$.

Ejercicio$\PageIndex{3}$

Utilice la notación de intervalos para describir la solución de:$x−7 < −8$.

Contestar: $(-\infty,-1)$

Si multiplicamos o dividimos ambos lados de una desigualdad por un número positivo, tenemos una desigualdad equivalente.

Multiplicar o dividir por un número positivo

Dejar$a$ y$b$ ser números reales con$a<b$. Si$c$ es un número positivo real, entonces\[a c<b c \nonumber \] y\[\dfrac{a}{c}<\dfrac{b}{c} \nonumber \]

Ejemplo$\PageIndex{4}$

Resuelva para$x : \quad 3 x \leq-9$ Sketch la solución en la línea real, luego use el generador de conjuntos y la notación de intervalos para describir su solución.

Solución

Para “deshacer” multiplicando por$3$, dividir ambos lados de la desigualdad por$3$. Debido a que estamos dividiendo ambos lados por un número positivo, no invertimos el signo de desigualdad.

\[\begin{aligned} 3x & \leq -9 & & \color {Red} \text { Original inequality. } \\ \dfrac{3x}{3} & \leq \dfrac{-9}{3} & & \color {Red} \text { Divide both sides by } 3. \\ x & \leq -3 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Sombra los números reales menores o iguales a$-3$.

$fig 2.6.e.png$

Usando la notación set-builder, la solución es$\{x : x \leq-3\}$. Usando la notación de intervalos, la solución es$(-\infty,-3]$.

Ejercicio$\PageIndex{4}$

Utilice la notación de intervalos para describir la solución de:\[2 x>-8 \nonumber \]

Contestar: $(-4, \infty)$

Revertir el signo de desigualdad

Hasta este punto, parece que la técnica para resolver desigualdades es prácticamente idéntica a la técnica utilizada para resolver ecuaciones. No obstante, en esta sección nos vamos a encontrar con una excepción.

Supongamos que comenzamos con la desigualdad válida$-2 < 5$, luego multiplicamos ambos lados por$2$,$3$, y$4$.

\[\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {2(-2)<2(5)} & {3(-2)<3(5)} & {4(-2)<4(5)} \\ {-4<10} & {-6<15} & {-8<20}\end{array} \nonumber \]

Obsérvese que en cada caso, la desigualdad resultante sigue siendo válida.

$\color{Red} \text {Caution! We’re about to make an error!} $

Empezar de nuevo con$−2 < 5$, pero esta vez multiplicar ambos lados por$−2$,$−3$, y$−4$.

\[\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {-2(-2)<-2(5)} & {\;-3(-2)<-3(5)} & {\;-4(-2)<-4(5)} \\ {4<-10} & {6<-15} & {8<-20}\end{array} \nonumber \]

¡En cada una de las desigualdades resultantes, el símbolo de la desigualdad señala el camino equivocado!

Cuando multiplicas ambos lados de una desigualdad por un número negativo, debes revertir el signo de desigualdad. Empezando por$−2 < 5$, multiplique ambos lados por$−2$,$−3$, y$−4$, pero invierta el símbolo de desigualdad.

Algunos lectores podrían preferir una razón más formal de por qué invertimos la desigualdad cuando multiplicamos ambos lados por un número negativo. Supongamos que$a<b$. Entonces, restar$b$ de ambos lados da el resultado$a−b<0$. Esto quiere decir que$a−b$ es un número negativo. Ahora bien, si$c$ es un número negativo, entonces el producto$(a−b)c$ es positivo. Entonces:

\[\begin{aligned}(a-b) c &>0 \\ a c-b c &>0 \\ a c-b c+b c &>0+b c \\ a c &>b c \end{aligned} \nonumber \]

Así, si empiezas con$a<b$ y$c<0$, entonces$ac > bc$.

Multiplicar o dividir por un número negativo

Dejar$a$ y$b$ ser números reales con$a<b$. Si$c$ es un número negativo real, entonces\[a c>b c \nonumber \] y Es\[\dfrac{a}{c}>\dfrac{b}{c} \nonumber \] decir, al multiplicar o dividir ambos lados de una desigualdad por un número negativo, se debe revertir el signo de desigualdad.

Ejemplo$\PageIndex{5}$

Resolver para$x: \quad −2x<4$. Esboce la solución en la línea real, luego use el generador de conjuntos y la notación de intervalos para describir su solución.

Solución

Para “deshacer” multiplicando por$−2$, dividir ambos lados por$−2$. Debido a que estamos dividiendo ambos lados por un número negativo, invertimos el signo de desigualdad.

\[\begin{aligned} -2 x&< 4 & & \color {Red} \text { Original inequality. } \\ \dfrac{-2x}{-2}&> \dfrac{4}{-2} & & \color {Red} \text { Divide both sides by }-2 \\ x&> -2 & & \color {Red} \text { Reverse the inequality sign. } \\ x&> -2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Sombra los números reales mayores que$−2$.

$fig 2.6.f.png$

Usando la notación set-builder, la solución es$\{x : x>-2\}$. Usando la notación de intervalos, la solución es$(-2, \infty)$.

Ejercicio$\PageIndex{5}$

Utilice la notación de intervalos para describir la solución de:\[−3x≥− 6 \nonumber \]

Contestar: $(-\infty, 2]$

Múltiples pasos

En ocasiones es necesario realizar una secuencia de pasos para llegar a la solución.

Ejemplo$\PageIndex{6}$

Resolver para$x: \quad 2 x +5> −7$. Esboce la solución en la línea real, luego use el generador de conjuntos y la notación de intervalos para describir su solución.

Solución

Para “deshacer” sumar$5$, restar$5$ de ambos lados de la desigualdad.

\[\begin{aligned} 2x+5&> -7 & & \color {Red} \text { Original inequality. } \\ 2x+5-5&> -7-5 & & \color {Red} \text { Subtract } 5 \text { from both sides. } \\ 2x&> -12 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Para “deshacer” multiplicando por$2$, dividir ambos lados por$2$. Debido a que estamos dividiendo ambos lados por un número positivo, no invertimos el signo de desigualdad.

\[\begin{aligned} \dfrac{2x}{2}& >\dfrac{-12}{2} & & \color {Red} \text { Divide both sides by } 2 \\ x&> -6 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Sombra los números reales mayores que$−6$.

$fig 2.6.g.png$

Usando la notación set-builder, la solución es$\{x : x>-6\}$. Usando la notación de intervalos, la solución es$(-6, \infty)$.

Ejercicio$\PageIndex{6}$

Utilice la notación de intervalos para describir la solución de:\[3x-2 ≤4 \nonumber \]

Contestar: $(-\infty, 2]$

Ejemplo$\PageIndex{7}$

Resolver para$x: \quad 3 −5x ≤ 2x + 17$. Esboce la solución en la línea real, luego use el generador de conjuntos y la notación de intervalos para describir su solución.

Solución

Necesitamos aislar términos que contengan$x$ en un lado de la desigualdad. Empezar restando$2x$ de ambos lados de la desigualdad.

\[\begin{aligned} 3-5x &\leq 2x+17 & & \color {Red} \text { Original inequality. } \\ 3-5x-2x &\leq 2x+17-2x & & \color {Red} \text { Subtract } 2x \text { from both sides. } \\ 3-7x &\leq 17 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Seguimos aislando términos que contienen$x$ en un lado de la desigualdad. Restar$3$ de ambos lados.

\[\begin{aligned} 3-7x-3 &\leq 17-3 & & \color {Red} \text { Subtract } 3 \text { from both sides. } \\ -7x &\leq 14 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Para “deshacer” multiplicando por$−7$, dividir ambos lados por$−7$. Debido a que estamos dividiendo ambos lados por un número negativo, invertimos el signo de desigualdad.

\[\begin{aligned} \dfrac{-7x}{-7} &\geq \dfrac{14}{-7} & & \color {Red} \text { Divide both sides by }-7 \\ x &\geq-2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

$fig 2.6.h.png$

Usando la notación set-builder, la solución es$\{x : x \geq-2\}$. Usando la notación de intervalos, la solución es$[-2, \infty)$.

Ejercicio$\PageIndex{7}$

Utilice la notación de intervalos para describir la solución de:\[4-x>2x +1 \nonumber \]

Contestar: $(-\infty, 1)$

Despejamos fracciones de una desigualdad de la manera habitual, multiplicando ambas partes por el mínimo denominador común.

Ejemplo$\PageIndex{8}$

Resolver para$x : \quad \quad \dfrac{3}{4}-\dfrac{x}{12}>\dfrac{1}{3}$.

Solución

Primero, despejar las fracciones de la desigualdad multiplicando ambos lados por el mínimo denominador común, que en este caso lo es$12$.

\[\begin{aligned} \dfrac{3}{4}-\dfrac{x}{12} &>\dfrac{1}{3} & & \color {Red} \text { Original inequality. } \\ 12\left[\dfrac{3}{4}-\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & & \color {Red} \text { Multiply both sides by } 12.\\ 12\left[\dfrac{3}{4}\right]-12\left[\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & & \color {Red} \text { Distribute the } 12.\\ 9-x &>4 & & \color {Red} \text { Cancel and Multiply. } \end{aligned} \nonumber \]

Para “deshacer” sumar$9$, restar$9$ de ambos lados.

\[\begin{aligned} 9-x-9 &> 4-9 & & \color {Red} \text { Subtract } 9 \text { from both sides. } \\ -x &> -5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Podríamos dividir ambos lados por$−1$, pero multiplicar ambos lados por también$−1$ hará el trabajo. Debido a que estamos multiplicando ambos lados por un número negativo, invertimos el signo de desigualdad.

\[\begin{aligned} (-1)(-x) &< (-5)(-1) & & \color {Red} \text { Multiply both sides by }-1. \text { Reverse the inequality sign. } \\ x &< 5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Sombra los números reales menos que$5$.

$fig 2.6.i.png$

Usando la notación set-builder, la solución es$\{x : x<5\}$. Usando la notación de intervalos, la solución es$(-\infty, 5)$.

Ejercicio$\PageIndex{8}$

Utilice la notación de intervalos para describir la solución de:\[\dfrac{2 x}{3}-\dfrac{3}{4} \geq-\dfrac{3}{2} \nonumber \]

Contestar: $[-\frac{9}{8}, \infty)$

Despejamos decimales de una desigualdad de la manera habitual, multiplicando ambos lados por el poder apropiado de diez.

Ejemplo$\PageIndex{9}$

Resolver para$x : \quad 3.25-1.2 x>4.6$.

Solución

Primero, despeja los decimales de la desigualdad multiplicando ambos lados por$100$, lo que mueve cada punto decimal dos lugares a la derecha.

\[\begin{aligned} 3.25-1.2 x &>4.6 & & \color {Red} \text { Original inequality. }\\ 325-120 x &>460 & & \color {Red} \text { Multiply both sides by } 100.\\ 325-120 x-325 &>460-325 & & \color {Red} \text { Subtract } 325 \text { from both sides. }\\ -120 x &>135 & & \color {Red} \text { Simplify both sides. } \\ \dfrac{-120 x}{-120} &<\dfrac{135}{-120} & & \color {Red} \text { Divide both sides by } -120. \text { Reverse the inequality sign.}\\ x &<-\dfrac{27}{24} & & \color {Red} \text {Reduce to lowest terms.} \end{aligned} \nonumber \]

Sombra los números reales menos que$−27/24$.

$fig 2.6.j.png$

Usando la notación set-builder, la solución es$\{x : x<-27 / 24\}$. Usando la notación de intervalos, la solución es$(-\infty,-27 / 24)$.

Ejercicio$\PageIndex{9}$

Utilice la notación de intervalos para describir la solución de:\[2.3 x-5.62 \geq-1.4 \nonumber \]

Contestar: $\big[\frac{211}{115}, \infty\big)$

Tabla Resumen de Set-Builder y Notación de Intervalos

Una tabla resumida del conjunto constructor y notación de intervalo se presenta en Tabla$\PageIndex{1}$.

Tabla$\PageIndex{1}$: Ejemplos de set-builder y notación de intervalos.
Sombreado en la línea real	Constructor de conjuntos	Intervalo
$fig 2.6.k.png$	$\{x : x>-5\}$	$(-5, \infty)$
$fig 2.6.l.png$	$\{x : x \geq-5\}$	$[-5, \infty)$
$higo 2.6.m.png$	$\{x : x<-5\}$	$(-\infty,-5)$
$higo 2.6.m.png$	$\{x : x \leq-5\}$	$(-\infty,-5]$

Sombreado en la línea real	Constructor de conjuntos	Intervalo
$fig 2.6.k.png$	\(\{x : x>-5\}\)	\((-5, \infty)\)
$fig 2.6.l.png$	\(\{x : x \geq-5\}\)	\([-5, \infty)\)
$higo 2.6.m.png$	\(\{x : x<-5\}\)	\((-\infty,-5)\)
$higo 2.6.m.png$	\(\{x : x \leq-5\}\)	\((-\infty,-5]\)

Search

Text Color

Text Size

Margin Size

Font Type