6.E: Funciones Periódicas (Ejercicios)

6.1: Gráficas de las funciones de seno y coseno

En el capítulo sobre Funciones trigonométricas, examinamos funciones trigonométricas como la función sinusoidal. En esta sección, interpretaremos y crearemos gráficas de funciones sinusoidales y cosenales

Verbal

1) ¿Por qué las funciones seno y coseno se denominan funciones periódicas?

Responder

Las funciones seno y coseno tienen la propiedad que$f(x+P)=f(x)$ por cierto$P$. Esto significa que los valores de la función se repiten para cada$P$ unidad en el$x$ eje.

2) ¿Cómo se$y=\sin x$ compara la gráfica con la gráfica de$y=\cos x$? Explica cómo podrías traducir horizontalmente la gráfica de$y=\sin x$ para obtener$y=\cos x$.

3) Para la ecuación$A \cos(Bx+C)+D$,¿qué constantes afectan el rango de la función y cómo afectan al rango?

Responder

El valor absoluto de la constante$A$ (amplitud) aumenta el rango total y la constante$D$ (desplazamiento vertical) desplaza la gráfica verticalmente.

4) ¿Cómo se relaciona el rango de una función sinusoidal traducida con la ecuación?$y=A \sin(Bx+C)+D$?

5) ¿Cómo se puede utilizar el círculo unitario para construir la gráfica de$f(t)=\sin t$?

Responder

En el punto donde el lado terminal de$t$ intersecta el círculo unitario, se puede determinar que$\sin t$ es igual a la$y$ coordenada -del punto.

Gráfica

Para los siguientes ejercicios, grafica dos periodos completos de cada función y establece la amplitud, el periodo y la línea media. Indicar los$y$ valores máximo y mínimo y sus correspondientes$x$ -valores en un periodo para$x>0$. Redondear las respuestas a dos decimales si es necesario.

6)$f(x)=2\sin x$

7)$f(x)=\dfrac{2}{3}\cos x$

Responder

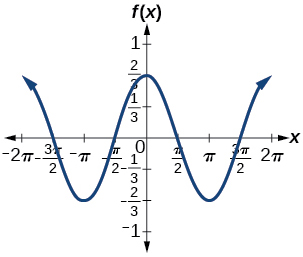
amplitud:$\dfrac{2}{3}$; periodo:$2\pi$; línea media:$y=0$; máximo:$y=\dfrac{2}{3}$ ocurre en$x=0$; mínimo:$y=-\dfrac{2}{3}$ ocurre en$x=\pi$; por un periodo, la gráfica comienza en$0$ y termina en$2\pi$.

8)$f(x)=-3\sin x$

9)$f(x)=4\sin x$

Responder

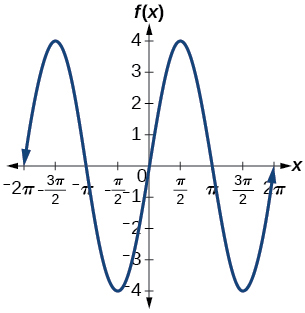
amplitud:$4$; periodo:$2\pi$; línea media:$y=0$; máximo$y=4$ ocurre en$x=\dfrac{\pi }{2}$; mínimo:$y=-4$ ocurre en$x=\dfrac{3\pi }{2}$; un período completo ocurre de$x=0$ a$x=2\pi$

10)$f(x)=2\cos x$

11)$f(x)=\cos (2x)$

Responder

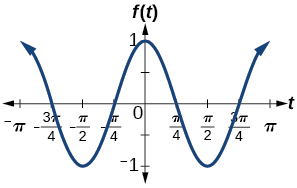
amplitud:$1$; periodo:$\pi$; línea media:$y=0$; máximo:$y=1$ ocurre en$x=\pi$; mínimo:$y=-1$ ocurre en$x=\dfrac{\pi }{2}$; un período completo se grafica de$x=0$ a$x=\pi$

 

 

 

 

 

 

 

12)$f(x)=2 \sin \left(\dfrac{1}{2}x\right)$

13)$f(x)=4 \cos(\pi x)$

Responder

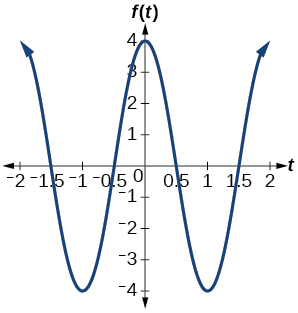
amplitud:$4$; periodo:$2$; línea media:$y=0$; máximo:$y=4$ ocurre en$x=0$; mínimo:$y=-4$ ocurre en$x=1$

14)$f(x)=3 \cos\left(\dfrac{6}{5}x\right)$

15)$y=3 \sin(8(x+4))+5$

Responder

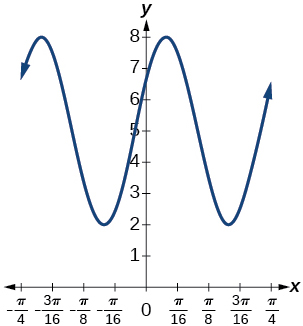
amplitud:$3$; periodo:$\dfrac{\pi}{4}$; línea media:$y=5$;
máximo:$y=8$ ocurre en$x = -4+\frac{21\pi}{16} \approx 0.123$;
mínimo:$y=2$ ocurre a$x = -4+\frac{23\pi}{16} \approx 0.516$; desplazamiento
horizontal:$-4$; traslación vertical$5$;
un periodo ocurre de$x=-4+\frac{22\pi}{16} \approx 0.320$ a$x=-4+\frac{26\pi}{16} \approx 1.105$

16)$y=2 \sin(3x-21)+4$

17)$y=5 \sin(5x+20)-2$

Responder

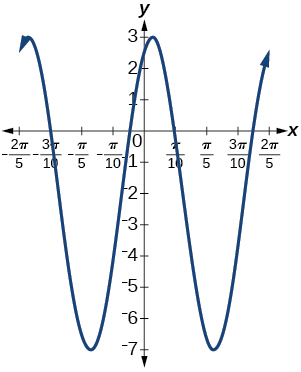
amplitud:$5$; periodo:$\dfrac{2\pi }{5}$; línea media:$y=-2$;
máximo:$y=3$ ocurre en$x= -4+\frac{13\pi}{10} \approx 0.084$;
mínimo:$y=-7$ ocurre en$x=-4+\frac{15\pi}{10} \approx 0.712$; desplazamiento de
fase:$-4$; traslación vertical:$-2$;
un periodo completo puede ser graficado$x=-4+\frac{7\pi}{5} \approx 0.398$ en$x=-4+\frac{9\pi}{5} \approx 1.655$

Para los siguientes ejercicios, grafica un periodo completo de cada función, comenzando en$x=0$.
Para cada función, indique la amplitud, el período y la línea media.
Indicar los$y$ valores máximo y mínimo y sus correspondientes$x$ -valores en un periodo para$x>0$.
Indicar el desplazamiento de fase y la traslación vertical, en su caso.
Redondear las respuestas a dos decimales si es necesario.

18)$f(t)=2\sin \left(t-\dfrac{5\pi}{6} \right)$

19)$f(t)=-\cos \left(t+\dfrac{\pi}{3} \right)+1$

Responder

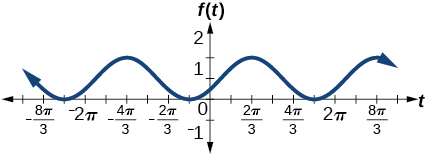
amplitud:$1$; periodo:$2\pi$; línea media:$y=1$;
máximo:$y=2$ ocurre en$t=\frac{2\pi}{3} \approx 2.094$;
mínimo:$y=0$ ocurre a$t=\frac{2\pi}{3} \approx5.24$; desplazamiento de
fase:$-\dfrac{\pi}{3}$; traslación vertical:$1$;
un periodo completo es de$t=\frac{2\pi}{3} \approx 2.094$ a$t=\frac{8\pi}{3} \approx 8.378$

20)$f(t)=4\cos \left(2\left (t+\dfrac{\pi}{4} \right ) \right)-3$

21)$f(t)=-\sin \left (\dfrac{1}{2}t+\dfrac{5\pi}{3} \right )$

Responder

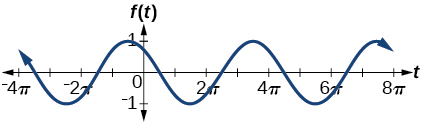amplitud:$1$; periodo:$4\pi$; línea media:$y=0$;
máximo:$y=1$ ocurre en$t=\frac{11\pi}{3} \approx 11.52$;
mínimo:$y=-1$ ocurre a$t=\frac{5\pi}{3} \approx 5.24$; desplazamiento de
fase:$-\dfrac{10\pi}{3}$; desplazamiento vertical:$0$;
un periodo completo es de $t=\frac{2\pi}{3} \approx 2.094$a$t=\frac{14\pi}{3} \approx 14.661$

22)$f(x)=4\sin \left (\dfrac{\pi}{2}(x-3) \right )+7$

23) Determinar la amplitud, línea media, punto y una ecuación que involucra la función sinusoidal para la gráfica que se muestra en la Figura siguiente.

Figura$\PageIndex{23}$

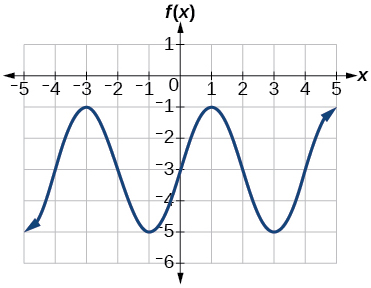
Responder

23. amplitud:$2$; línea media:$y=-3$ período:$4$; ecuación:$f(x)=2\sin \left (\dfrac{\pi}{2}x \right )-3$

24) Determinar la amplitud, línea media, punto y una ecuación que involucra la función coseno para la gráfica que se muestra en la Figura siguiente.

Figura$\PageIndex{24}$

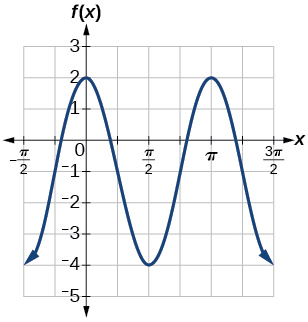
25) Determinar la amplitud, línea media, período y una ecuación que involucra la función coseno para la gráfica que se muestra en la Figura a continuación.

Figura$\PageIndex{25}$

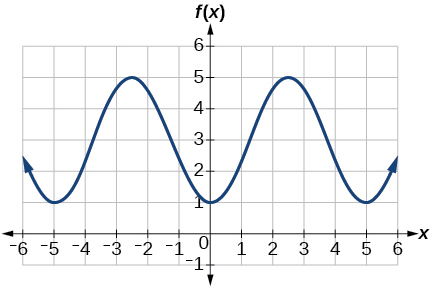
Responder

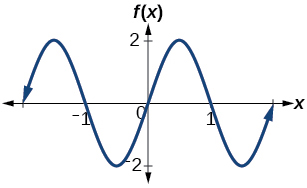
25. amplitud:$2$; periodo:$5$; línea media:$y=3$ ecuación:$f(x)=-2\cos \left (\dfrac{2\pi}{5}x \right )+3$

26) Determinar la amplitud, línea media, punto y una ecuación que involucre la función sinusoidal para la gráfica que se muestra en la Figura siguiente.

Figura$\PageIndex{26}$

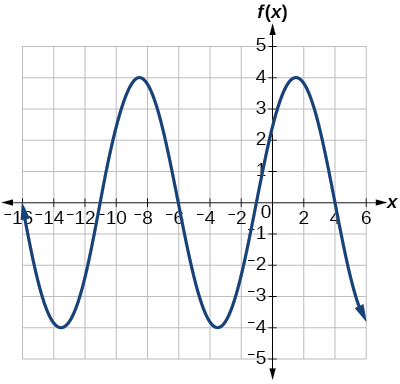
27) Determinar la amplitud, línea media, período y una ecuación que involucra la función coseno para la gráfica que se muestra en la Figura a continuación.

Figura$\PageIndex{27}$

Responder

27. amplitud:$4$; periodo:$2$; línea media:$y=0$; ecuación:$f(x)=-4\cos \left (\pi \left (x-\dfrac{\pi}{2} \right ) \right )$

28) Determinar la amplitud, línea media, punto y una ecuación que involucra la función sinusoidal para la gráfica que se muestra en la Figura a continuación.

Figura$\PageIndex{28}$

29) Determinar la amplitud, línea media, punto y una ecuación que involucra la función coseno para la gráfica que se muestra en la Figura siguiente.

Figura$\PageIndex{29}$

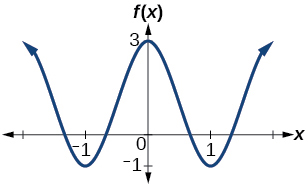
Responder

29. amplitud:$2$; periodo:$2$;$y=1$ ecuación de línea media:$f(x)=2\cos \left (\pi x \right )+1$

30) Determinar la amplitud, línea media, punto y una ecuación que involucre la función sinusoidal para la gráfica que se muestra en la Figura siguiente.

Figura$\PageIndex{30}$

Algebraico

Para los siguientes ejercicios, vamos$f(x)=\sin x$.

31) En$[0,2\pi )$,resolver$f(x)=0$.

32) En$[0,2\pi )$, resolver$f(x)=\dfrac{1}{2}$.

Responder

$\dfrac{\pi }{6}$,$\dfrac{5\pi }{6}$

 

 

 

 

 

 

 

33) Evaluar$f \left( \dfrac{\pi }{2} \right)$.

34) En$[0,2\pi)$,$f(x)=\dfrac{\sqrt{2}}{2}$. Encuentra todos los valores de$x$.

Responder

$\dfrac{\pi }{4}$,$\dfrac{3\pi }{4}$

 

 

 

35) En$[0,2\pi )$,el (los) valor (s) máximo (s) de la función ocurre (s) en qué$x$ -valor (s)?

 

 

 

36) En$[0,2\pi )$,el (los) valor (s) mínimo (s) de la función ocurre (s) en qué$x$ -valor (s)?

 

 

 

Responder

$\dfrac{3\pi }{2}$

 

 

 

37) Demostrar que$f(-x) = -f(x)$. Esto significa que$f(x)=\sin x$ es una función impar y posee simetría con respecto a ________________.

 

 

 

Para los siguientes ejercicios, vamos$f(x)=\cos x$

 

 

 

38) En$[0,2\pi )$,resolver la ecuación$f(x)=\cos x=0$

Responder

$\dfrac{\pi }{2}$,$\dfrac{3\pi }{2}$

 

 

 

39) En$[0,2\pi )$,resolver$f(x)=\dfrac{1}{2}$.

 

 

 

40) En$[0,2\pi )$,encontrar las$x$ -intercepciones de$f(x)=\cos x$.

 

 

 

Responder

$\dfrac{\pi }{2}$,$\dfrac{3\pi }{2}$

 

 

 

41) En$[0,2\pi )$,encontrar los$x$ -valores en los que la función tiene un valor máximo o mínimo.

 

 

 

42) En$[0,2\pi )$,resolver la ecuación$f(x)=\dfrac{\sqrt{3}}{2}$.

 

 

 

Responder

$\dfrac{\pi }{6}$,$\dfrac{11\pi }{6}$

 

 

 

Tecnología

 

 

 

43) Gráfica$h(x)=x+\sin x$ sobre$[0,2\pi ]$. Explique por qué la gráfica aparece como lo hace.

 

 

 

44) Gráfica$h(x)=x+\sin x$ sobre$[-100,100]$. ¿Apareció la gráfica como se predijo en el ejercicio anterior?

 

 

 

Responder

La gráfica aparece lineal. Las funciones lineales dominan la forma de la gráfica para grandes valores de$x$.

 

 

 

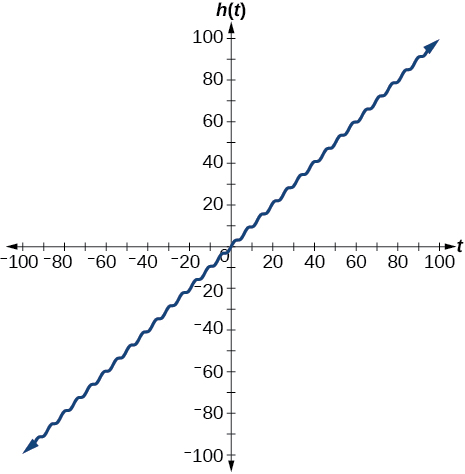
45) Graficar$f(x)=x\sin x$$[0,2\pi ]$ y verbalizar cómo varía la gráfica de la gráfica de$f(x)=x\sin x$.

 

 

 

46) Gráfica$f(x)=x\sin x$ en la ventana$[-10,10]$ y explica lo que muestra la gráfica.

 

 

 

Responder

La gráfica es simétrica con respecto al$y$ eje -y no hay amplitud porque la función no es periódica.

 

 

 

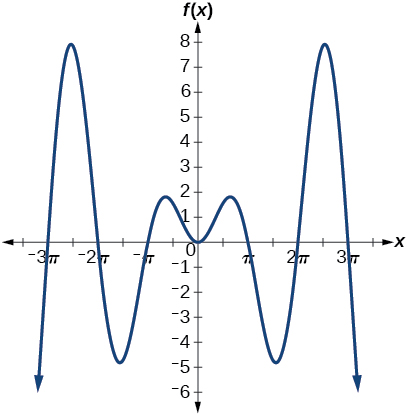
47) Gráfica$f(x)=\dfrac{\sin x}{x}$ en la ventana$[-5\pi , 5\pi ]$ y explica lo que muestra la gráfica.

 

 

 

Aplicaciones del mundo real

 

 

 

48) Una noria es de$25$ metros de diámetro y abordada desde una plataforma que se encuentra$1$ metros sobre el suelo. La posición de las seis en punto en la noria está nivelada con la plataforma de carga. La rueda completa la revolución$1$ completa en$10$ minutos. La función$h(t)$ da la altura de una persona en metros sobre el suelo$t$ minutos después de que la rueda comience a girar

 

 

 

1. Encuentra la amplitud, línea media, y periodo de$h(t)$.
2. Encuentra una fórmula para la función de altura$h(t)$.
3. ¿Qué tan alto del suelo está una persona después de$5$ minutos?

Responder

1. Amplitud:$12.5$; periodo:$10$; línea media:$y=13.5$
2. $h(t)=12.5\sin\left ( \dfrac{\pi}{5}(t-2.5) \right )+13.5$
3. $26$ft

 

 

 

6.2: Gráficas de las Otras Funciones Trigonométricas

 

 

 

Esta sección aborda la gráfica de las curvas tangente, cosecante, secante y cotangente.

 

 

 

Verbal

 

 

 

 

 

 

 

1) Explicar cómo se puede utilizar la gráfica de la función sinusoidal para graficar$y=\csc x$.

 

 

 

Responder

 

 

 

Dado que$y=\csc x$ es la función recíproca de$y=\sin x$, se puede trazar el recíproco de las coordenadas en la gráfica de$y=\sin x$ obtener las$y$ coordenadas -de$y=\csc x$. Las$x$ -intercepciones de la gráfica$y=\sin x$ son las asíntotas verticales para la gráfica de$y=\csc x$.

 

 

 

2) ¿Cómo se$y=\cos x$ puede utilizar la gráfica de para construir la gráfica de$y=\sec x$?

 

 

 

3) Explicar por qué el periodo de$y=\tan x$ es igual a$\pi$.

 

 

 

Responder

 

 

 

Las respuestas variarán. Usando el círculo unitario, se puede mostrar eso$y=\tan (x+\pi )=\tan x$.

 

 

 

4) ¿Por qué no hay intercepciones en la gráfica de$y=\csc x$?

 

 

 

5) ¿Cómo se$y=\csc x$ compara el periodo de con el periodo de$y=\sin x$?

 

 

 

Responder

 

 

 

El periodo es el mismo:$2\pi$

 

 

 

Algebraico

 

 

 

Para los ejercicios 6-9, haga coincidir cada función trigonométrica con una de las siguientes gráficas.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

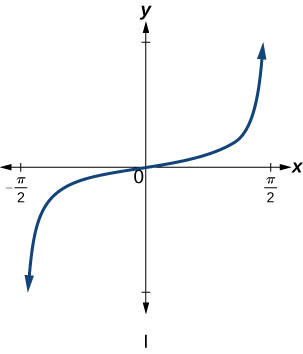
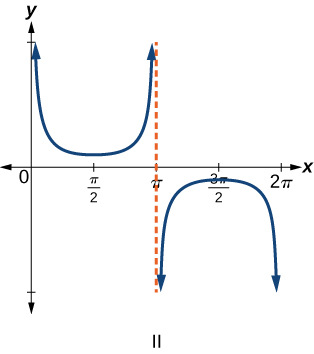
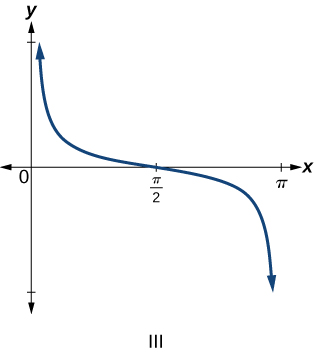
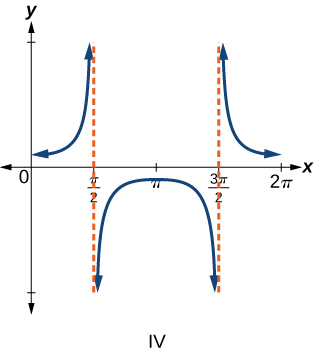
6)$f(x)=\tan x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7)$f(x)=\sec x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Responder

$\mathrm{IV}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8)$f(x)=\csc x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9)$f(x)=\cot x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Responder

$\mathrm{III}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Para los ejercicios 10-16, encuentra el periodo y el desplazamiento horizontal de cada una de las funciones.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

10)$f(x)=2\tan(4x-32)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11)$h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Responder

periodo:$8$; desplazamiento horizontal:$1$ unidad a izquierda

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12)$m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

13) Si$\tan x=-1.5$, encontrar$\tan (-x)$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Responder

$1.5$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

14) Si$\sec x=2$, encuentra$\sec (-x)$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15) Si$\csc x=-5$, encuentra$\csc (-x)$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Responder

$5$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

16) Si$x\sin x=2$, encuentra$(-x)\sin (-x)$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Para los ejercicios 17-18, reescribe cada expresión de tal manera que el argumento$x$ sea positivo.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

17)$\cot(-x)\cos(-x)+\sin(-x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

$-\cot x \cos x-\sin x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

18)$\cos(-x)+\tan(-x)\sin(-x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Gráfica

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Para los ejercicios 19-36, esbozar dos periodos de la gráfica para cada una de las siguientes funciones. Identificar el factor de estiramiento, periodo y asíntotas.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

19)$f(x)=2\tan(4x-32)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

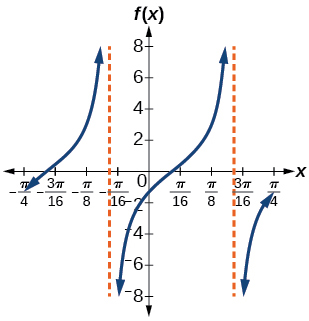
factor de estiramiento:$2$; periodo:$\dfrac{\pi }{3}$; asíntotas:$x=\dfrac{1}{4}\left(\dfrac{\pi }{2}+\pi k \right)+8$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

20)$h(x)=2\sec\left(\dfrac{\pi }{4}(x+1) \right)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

21)$m(x)=6\csc\left(\dfrac{\pi }{3}x+\pi \right)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

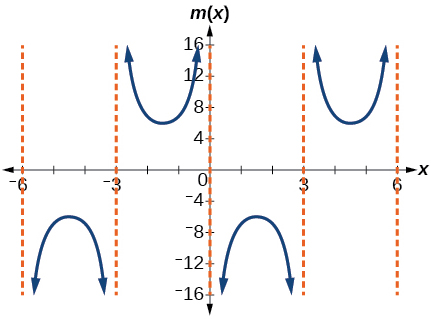
factor de estiramiento:$6$; período:$6$; asíntotas:$x=k$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

22)$j(x)=\tan \left ( \dfrac{\pi }{2}x \right )$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

23)$p(x)=\tan \left ( x-\dfrac{\pi }{2} \right )$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

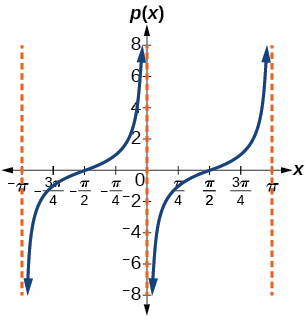
factor de estiramiento:$1$; periodo:$\pi$; asíntotas:$x=\pi k$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

24)$f(x)=4\tan (x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

25)$f(x)=\tan \left ( x+\dfrac{\pi }{4} \right )$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

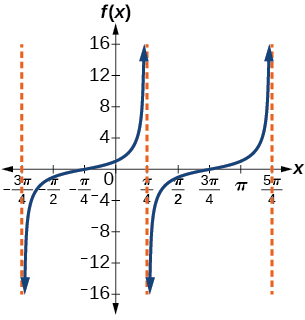
Factor de estiramiento:$1$; periodo:$\pi$; asíntotas:$x=\dfrac{\pi}{4}+\pi k$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

26)$f(x)=\pi \tan(\pi x- \pi)-\pi$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

27)$f(x)=2\csc (x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

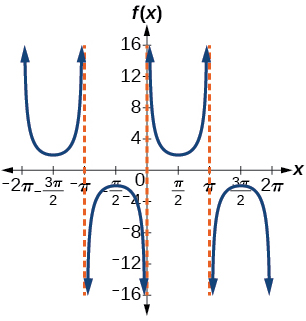
factor de estiramiento:$2$; periodo:$2\pi$; asíntotas:$x=\pi k$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

28)$f(x)=-\dfrac{1}{4}\csc(x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

29)$f(x)=4\sec(3x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

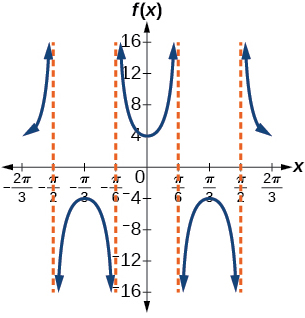
factor de estiramiento:$4$; periodo:$\dfrac{2\pi }{3}$; asíntotas:$x=\dfrac{\pi }{6}k$, donde$k$ es un entero impar

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

30)$f(x)=-3\cot(2x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

31)$f(x)=7\sec(5x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

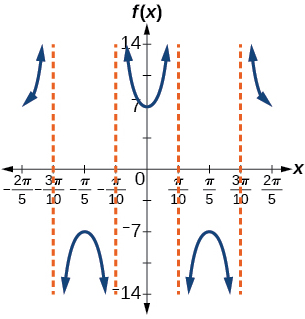
factor de estiramiento:$7$; periodo:$\dfrac{2\pi }{5}$; asíntotas:$x=\dfrac{\pi }{10}k$, donde$k$ es un entero impar

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

32)$f(x)=\dfrac{9}{10}\csc(\pi x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

33)$f(x)=2\csc \left(x+\dfrac{\pi }{4} \right)-1$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

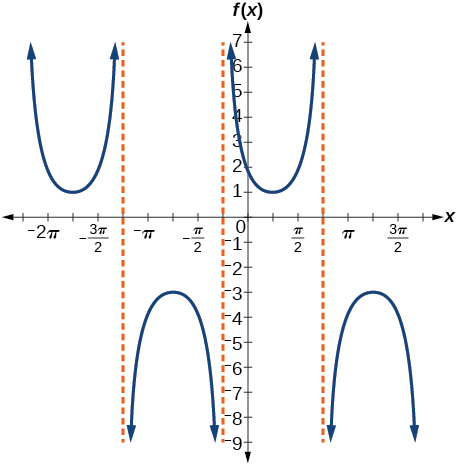
Factor de estiramiento:$2$; período:$2\pi$; asíntotas:$x=-\dfrac{\pi}{4}+\pi k$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

34)$f(x)=-\sec \left(x-\dfrac{\pi }{3} \right)-2$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

35)$f(x)=\dfrac{7}{5}\csc \left(x-\dfrac{\pi }{4} \right)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

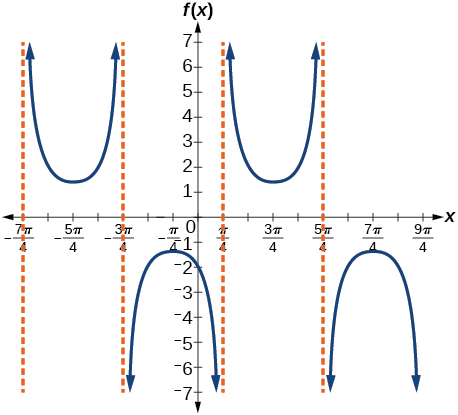
Factor de estiramiento:$\dfrac{7}{5}$; período:$2\pi$; asíntotas:$x=\dfrac{\pi}{4}+\pi k$, donde$k$ es un entero

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

36)$f(x)=5\left (\cot \left(x+\dfrac{\pi }{2} \right) -3 \right )$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

37) Una curva tangente,$A=1$, periodo de$\dfrac{\pi }{3}$; y desplazamiento de fase$(h, k)=\left ( \dfrac{\pi }{4},2 \right )$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

$y=\tan\left(3\left(x-\dfrac{\pi}{4} \right) \right)+2$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

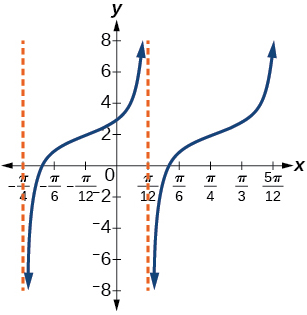
38) Una curva tangente$A=-2$, período de$\dfrac{\pi }{4}$; y desplazamiento de fase$(h, k)=\left (- \dfrac{\pi }{4},-2 \right )$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Para los ejercicios 39-45, encuentra una ecuación para la gráfica de cada función.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

39)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

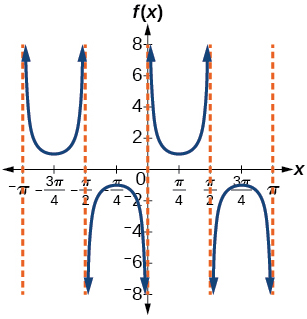
Contestar

$f(x)=\csc (2x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

40)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

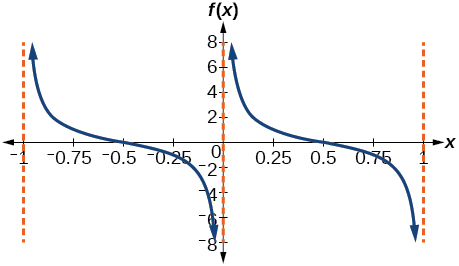
41)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

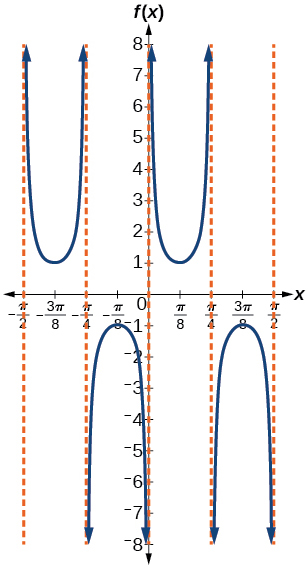
Contestar

$f(x)=\csc (4x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

42)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

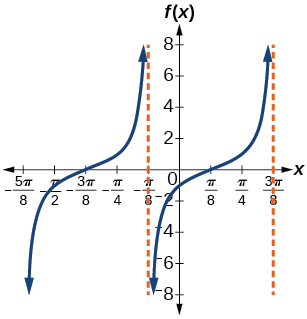
43)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

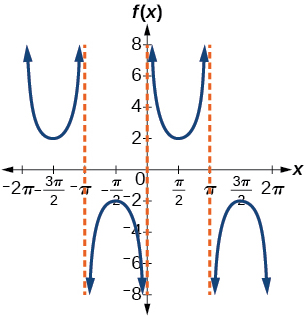
Contestar

$f(x)=2\csc x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

44)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

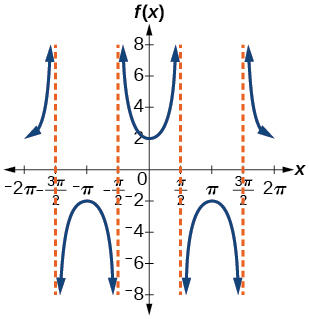
45)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

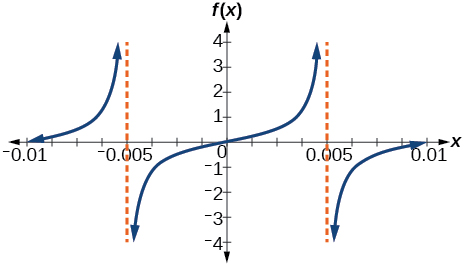
Contestar

$f(x)=\dfrac{1}{2}\tan (100\pi x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Tecnología

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Para los ejercicios 46-53, utilice una calculadora gráfica para graficar dos periodos de la función dada. Nota: la mayoría de las calculadoras gráficas no tienen un botón cosecante; por lo tanto, necesitará ingresar$\csc x$ como$\dfrac{1}{\sin x}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

46)$f(x)=| \csc (x) |$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

47)$f(x)=| \cot (x) |$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

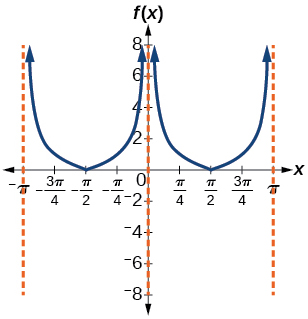
48)$f(x)=2^{\csc (x)}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

49)$f(x)=\frac{\csc (x)}{\sec (x)}$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

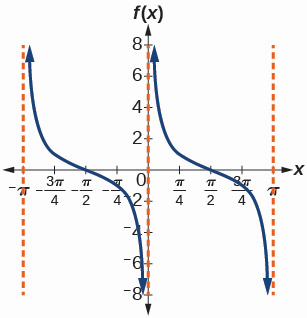
50) Gráfica$f(x)=1+\sec^2(x)-\tan^2(x)$. ¿Cuál es la función que se muestra en la gráfica?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

51)$f(x)=\sec(0.001x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

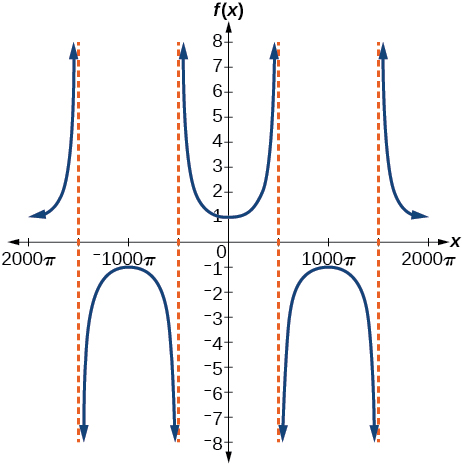
52)$f(x)=\cot(100 \pi x)$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

53)$f(x)=\sin^2x +\cos^2x$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Aplicaciones del mundo real

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

54) La función$f(x)=20\tan\left(\dfrac{\pi }{10}x\right)$ marca la distancia en el movimiento de un haz de luz desde un carro de policía a través de una pared por tiempo$x$, en segundos, y distancia$f(x)$,en pies.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Gráfica sobre el intervalo$[0,5]$
2. Encontrar e interpretar el factor de estiramiento, periodo y asíntota.
3. Evaluar$f(10)$$f(2.5)$ y discutir los valores de la función en esas entradas.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

55) De pie en la orilla de un lago, un pescador mira un barco muy lejos a su izquierda. Vamos$x$, medido en radianes, sea el ángulo formado por la línea de visión hacia el buque y una línea que va hacia el norte desde su posición. Supongamos que el norte debido$x$ es$0$ y se mide negativo a la izquierda y positivo a la derecha. (Ver Figura abajo.) El barco viaja desde el oeste hacia el este y, ignorando la curvatura de la Tierra, la distancia$d(x)$, en kilómetros, desde el pescador hasta la embarcación viene dada por la función$d(x)=1.5\sec(x)$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. ¿Para qué es un dominio razonable$d(x)$?
2. Gráfica$d(x)$ sobre este dominio.
3. Encuentra y discute el significado de cualquier asíntota vertical en la gráfica de$d(x)$.
4. Calcular e interpretar$d\left ( -\dfrac{\pi }{3} \right )$. Redondear a la segunda posición decimal.
5. Calcular e interpretar$d\left ( \dfrac{\pi }{6} \right )$. Redondear a la segunda posición decimal.
6. ¿Cuál es la distancia mínima entre el pescador y el barco? ¿Cuándo ocurre esto?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

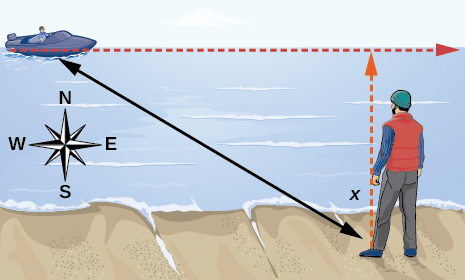
Contestar

1. $\left ( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right )$
2. 
3. $x=-\dfrac{\pi }{2}$y$x=\dfrac{\pi }{2}$; la distancia crece sin ataduras a medida que$| x |$ se acerca$\dfrac{\pi }{2}$ —es decir, en ángulo recto con la línea que representa hacia el norte, la embarcación estaría tan lejos, el pescador no la podía ver;
4. $3$; cuando$x=-\dfrac{\pi }{3}$, el barco está$3$ a km de distancia;
5. $1.73$; cuando$x=\dfrac{\pi }{6}$, el barco está$1.73$ a unos km de distancia;
6. $1.5$km; cuando$x=0$

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

56) Un telémetro láser está bloqueado en un cometa que se aproxima a la Tierra. La distancia$g(x)$, en kilómetros, del cometa después de$x$ días, pues$x$ en el intervalo$0$ a$30$ días, está dado por$g(x)=250,000\csc \left(\dfrac{\pi }{30}x \right)$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Gráfica$g(x)$ sobre el intervalo$[0,35]$.
2. Evaluar$g(5)$ e interpretar la información.
3. ¿Cuál es la distancia mínima entre el cometa y la Tierra? ¿Cuándo ocurre esto? ¿A qué constante en la ecuación corresponde esto?
4. Encontrar y discutir el significado de cualquier asíntota vertical.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

57) Una cámara de video se enfoca en un cohete en una plataforma de lanzamiento$2$ a millas de la cámara. El ángulo de elevación desde el suelo hasta el cohete después de$x$ segundos es$\dfrac{\pi }{120}x$.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Escribir una función que exprese la altitud$h(x)$, en millas, del cohete sobre el suelo después de$x$ segundos. Ignorar la curvatura de la Tierra.
2. Gráfica$h(x)$ sobre el intervalo$(0,60)$.
3. Evaluar e interpretar los valores$h(0)$ y$h(30)$.
4. ¿Qué pasa con los valores de$h(x)$ como se$x$ acerca a los$60$ segundos? Interpretar el significado de esto en términos del problema.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Contestar

1. $h(x)=2\tan \left(\dfrac{\pi }{120}x \right)$
2. 
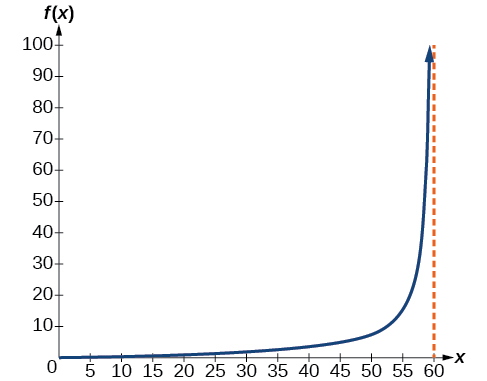
3. $h(0)=0$: después de$0$ segundos, el cohete está$0$ mi sobre el suelo;$h(30)=2$: después de$30$ segundos, los cohetes están$2$ a mi altura;
4. A medida que$x$ se acerca a los$60$ segundos, los valores de$h(x)$ crecen cada vez más. La distancia al cohete es cada vez mayor que la cámara ya no puede rastrearlo.

 

6.3: Funciones trigonométricas inversas

 

En esta sección, exploraremos las funciones trigonométricas inversas. Las funciones trigonométricas inversas “deshacen” lo que “hace” la función trigonométrica original, como ocurre con cualquier otra función y su inversa. En otras palabras, el dominio de la función inversa es el rango de la función original, y viceversa.

 

Verbal

 

1) ¿Por qué las funciones$f(x)=\sin^{-1}x$ y$g(x)=\cos^{-1}x$ tienen diferentes rangos?

 

Contestar

La función$y=\sin x$ es uno a uno en$\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]$; por lo tanto, este intervalo es el rango de la función inversa de$y=\sin x$,$f(x)=\sin^{-1}x$ La función$y=\cos x$ es uno a uno en$[0,\pi ]$; por lo tanto, este intervalo es el rango de la función inversa de$y=\cos x$,$f(x)=\cos^{-1}x$

 

2) Dado que las funciones$y=\cos x$ y$y=\cos^{-1}x$ son funciones inversas, ¿por qué es$\cos^{-1}\left (\cos \left (-\dfrac{\pi }{6} \right ) \right )$ no es igual a$-\dfrac{\pi }{6}$?

 

3) Explicar el significado de$\dfrac{\pi }{6}=\arcsin (0.5)$.

 

Contestar

$\dfrac{\pi }{6}$es la medida radianes de un ángulo entre$-\dfrac{\pi }{2}$ y$\dfrac{\pi }{2}$ cuyo seno es$0.5$.

 

4) La mayoría de las calculadoras no tienen una clave para evaluar$\sec ^{-1}(2)$. Explique cómo se puede hacer esto usando la función coseno o la función coseno inversa.

 

5) ¿Por qué debe funcionar el dominio del seno,$\sin x$, estar restringido a$\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]$ para que exista la función sinusoidal inversa?

 

Contestar

Para que cualquier función tenga un inverso, la función debe ser uno a uno y debe pasar la prueba de línea horizontal. La función sinusoidal regular no es uno a uno a menos que su dominio esté restringido de alguna manera. Los matemáticos han acordado restringir la función sinusoidal al intervalo para$\left [ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right ]$ que sea uno a uno y posea una inversa.

 

6) Discutir por qué esta afirmación es incorrecta:$\arccos(\cos x)=x$ para todos$x$.

 

7) Determina si la siguiente afirmación es verdadera o falsa y explica tu respuesta:$\arccos(-x)=\pi - \arccos x$

 

Contestar

Cierto. El ángulo,$\theta _1$ que es igual$\arccos(-x)$,$x>0$, será un segundo ángulo cuadrante con ángulo de referencia,$\theta _2$, donde$\theta _2$ es igual$\arccos x$,$x>0$. Dado que$\theta _2$ es el ángulo de referencia para$\theta _1$,$\theta _2=\pi - \theta _1$ y$\arccos(-x)=\pi - \arccos x-$

 

Algebraico

 

Para los ejercicios 8-16, evaluar las expresiones.

 

8)$\sin^{-1}\left(\dfrac{\sqrt{2}}{2}\right)$

 

9)$\sin^{-1}\left(-\dfrac{1}{2}\right)$

 

Contestar

$-\dfrac{\pi }{6}$

 

10)$\cos^{-1}\left(-\dfrac{1}{2}\right)$

 

11)$\cos^{-1}\left(-\dfrac{\sqrt{2}}{2}\right)$

 

Contestar

$\dfrac{3\pi }{4}$

 

12)$\tan^{-1}(1)$

 

13)$\tan^{-1}(-\sqrt{3})$

 

Contestar

$-\dfrac{\pi }{3}$

 

14)$\tan^{-1}(-1)$

 

15)$\tan^{-1}(\sqrt{3})$

 

Contestar

$\dfrac{\pi }{3}$

 

16)$\tan^{-1}\left(\dfrac{-1}{\sqrt{3}}\right)$

 

Para los ejercicios 17-21, utilice una calculadora para evaluar cada expresión. Expresar respuestas a la centésima más cercana.

 

17)$\cos^{-1}(-0.4)$

 

Contestar

$1.98$

 

18)$\arcsin (0.23)$

 

19)$\arccos \left(\dfrac{3}{5}\right)$

 

Contestar

$0.93$

 

20)$\cos^{-1}(-0.8)$

 

21)$\tan^{-1}(6)$

 

Contestar

$1.41$

 

Para los ejercicios 22-23, encuentra el ángulo$\theta$ en el triángulo rectángulo dado. Respuestas redondas a la centésima más cercana.

 

22)

 

 

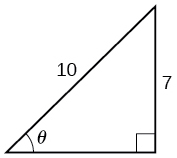
23)

 

 

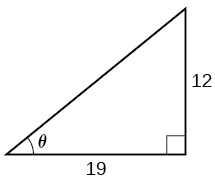
Contestar

$0.56$radianes

 

Para los ejercicios 24-36, encuentra el valor exacto, si es posible, sin calculadora. Si no es posible, explique por qué.

 

24)$\sin^{-1}(\cos(\pi))$

 

25)$\tan^{-1}(\sin(\pi))$

 

Contestar

$0$

 

26)$\cos^{-1}\left(\sin \left(\dfrac{\pi}{3} \right)\right)$

 

27)$\tan^{-1}\left(\sin \left(\dfrac{\pi}{3} \right)\right)$

 

Contestar

$0.71$

 

28)$\sin^{-1}\left(\cos \left(\dfrac{-\pi}{2} \right)\right)$

 

29)$\tan^{-1}\left(\sin \left(\dfrac{4\pi}{3} \right)\right)$

 

Contestar

$-0.71$

 

30)$\sin^{-1}\left(\sin \left(\dfrac{5\pi}{6} \right)\right)$

 

31)$\tan^{-1}\left(\sin \left(\dfrac{-5\pi}{2} \right)\right)$

 

Contestar

$-\dfrac{\pi}{4}$

 

32)$\cos \left(\sin^{-1} \left(\dfrac{4}{5} \right)\right)$

 

33)$\sin \left(\cos^{-1} \left(\dfrac{3}{5} \right)\right)$

 

Contestar

$0.8$

 

34)$\sin \left(\tan^{-1} \left(\dfrac{4}{3} \right)\right)$

 

35)$\cos \left(\tan^{-1} \left(\dfrac{12}{5} \right)\right)$

 

Contestar

$\dfrac{5}{13}$

 

36)$\cos \left(\sin^{-1} \left(\dfrac{1}{2} \right)\right)$

 

Para los ejercicios 37-41, encuentra el valor exacto de la expresión en términos de$x$ con la ayuda de un triángulo de referencia.

 

37)$\tan \left(\sin^{-1} (x-1)\right)$

 

Contestar

$\dfrac{x-1}{\sqrt{-x^2+2x}}$

 

38)$\sin \left(\sin^{-1} (1-x)\right)$

 

39)$\cos \left(\sin^{-1} \left(\dfrac{1}{x}\right)\right)$

 

Contestar

$\dfrac{\sqrt{x^2-1}}{x}$

 

40)$\cos \left(\tan^{-1} (3x-1)\right)$

 

41)$\tan \left(\sin^{-1} \left(x+\dfrac{1}{2}\right)\right)$

 

Contestar

$\dfrac{x+0.5}{\sqrt{-x^2-x+\tfrac{3}{4}}}$

 

Extensiones

 

Para el ejercicio 42, evaluar la expresión sin usar calculadora. Dar el valor exacto.

 

2)$\dfrac{\sin^{-1}\left ( \tfrac{1}{2} \right )-\cos^{-1}\left ( \tfrac{\sqrt{2}}{2} \right )+\sin^{-1}\left ( \tfrac{\sqrt{3}}{2} \right )-\cos^{-1}(1)}{\cos^{-1}\left ( \tfrac{\sqrt{3}}{2} \right )-\sin^{-1}\left ( \tfrac{\sqrt{2}}{2} \right )+\cos^{-1}\left ( \tfrac{1}{2} \right )-\sin^{-1}(0)}$

 

Para los ejercicios 43-47, encuentra la función si $\sin t = \dfrac{x}{x+1}$

 

43)$\cos t$

 

Contestar

$\dfrac{\sqrt{2x+1}}{x+1}$

 

44)$\sec t$

 

45)$\cot t$

 

Contestar

$\dfrac{\sqrt{2x+1}}{x}$

 

46)$\cos \left(\sin^{-1} \left(\dfrac{x}{x+1}\right)\right)$

 

47)$\tan^{-1} \left(\dfrac{x}{\sqrt{2x+1}}\right)$

 

Contestar

$t$

 

Gráfica

 

48) Graficar$y=\sin^{-1} x$ y declarar el dominio y rango de la función.

 

49) Gráfica$y=\arccos x$ y declarar el dominio y el rango de la función.

 

Contestar

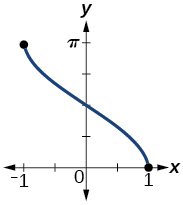
dominio$[-1,1]$; gama$[0,\pi ]$

 

50) Graficar un ciclo$y=\tan^{-1} x$ y declarar el dominio y rango de la función.

 

51) ¿Por qué valor de$x$ hace$\sin x=\sin^{-1} x$? Utilice una calculadora gráfica para aproximar la respuesta.

 

Contestar

aproximadamente$x=0.00$

 

52) ¿Por qué valor de$x$ hace$\cos x=\cos^{-1} x$? Utilice una calculadora gráfica para aproximar la respuesta.

 

Aplicaciones del mundo real

 

53) Supongamos que una escalera de$13$ pie está apoyada contra un edificio, llegando al fondo de una ventana$12$ de segundo piso por encima del suelo. ¿Qué ángulo, en radianes, hace la escalera con el edificio?

 

Contestar

 

$0.395$radianes

 

54) Supongamos que conduce$0.6$ millas en una carretera para que la distancia vertical cambie de$0$ a$150$ pies. ¿Cuál es el ángulo de elevación de la carretera?

 

55) Un triángulo isósceles tiene dos lados congruentes de$9$ pulgadas de largo. El lado restante tiene una longitud de$8$ pulgadas. Encuentra el ángulo que hace un lado de$9$ pulgadas con el lado$8$ -inch.

 

Contestar

$1.11$radianes

 

56) Sin usar una calculadora, aproximar el valor de$\arctan (10,000)$. Explica por qué tu respuesta es razonable.

 

57) Un truss para el techo de una casa se construye a partir de dos triángulos rectos idénticos. Cada uno tiene una base de$12$ pies y altura de$4$ pies. Encuentra la medida del ángulo agudo adyacente al lado$4$ -pie.

 

Contestar

$1.25$radianes

 

58) La línea$y=\dfrac{3}{5}x$ pasa por el origen en el$x,y$ plano. ¿Cuál es la medida del ángulo que hace la línea con el$x$ eje positivo?

 

59) La línea$y=\dfrac{-3}{7}x$ pasa por el origen en el$x,y$ plano. ¿Cuál es la medida del ángulo que hace la línea con el$x$ eje negativo?

 

Contestar

$0.405$radianes

 

60) ¿Qué grado porcentual debe tener una carretera si el ángulo de elevación de la carretera es de$4$ grados? (El grado porcentual se define como el cambio en la altitud de la carretera sobre una distancia horizontal de$100$ -pie. Por ejemplo, una$5\%$ pendiente significa que la carretera se eleva$5$ pies por cada$100$ pie de distancia horizontal.)

 

61) Una escalera$20$ de pie se apoya contra el costado de un edificio para que el pie de la escalera quede a$10$ pies de la base del edificio. Si las especificaciones exigen que el ángulo de elevación de la escalera esté entre$35$ y$45$ grados, ¿la colocación de esta escalera satisface las especificaciones de seguridad?

 

Contestar

No. El ángulo que hace la escalera con la horizontal es$60$ grados.

 

62) Supongamos que una escalera de$15$ pie se apoya contra el costado de una casa para que el ángulo de elevación de la escalera sea de$42$ grados. ¿A qué distancia está el pie de la escalera del costado de la casa?

 

Colaboradores y Atribuciones

 

• Template:OpenStaxPreCalc

 

 

 

Colaboradores y Atribuciones

 

• Template:OpenStaxPreCalc