6.R: Funciones Periódicas (Revisión)

Última actualización
Guardar como PDF

Page ID: 121306

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

6.1: Gráficas de las funciones de seno y coseno

Para los ejercicios 1-8, grafica las funciones durante dos periodos y determina el factor de amplitud o estiramiento, el periodo, la ecuación de la línea media y las asíntotas.

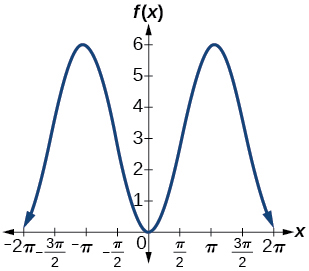
1)$f(x)=-3\cos x+3$

Contestar

amplitud:$3$; periodo:$2\pi $; línea media:$y=3$; sin asíntotas

$6R6.1.1.png$

2)$f(x)=\dfrac{1}{4}\sin x$

3)$f(x)=3\cos\left ( x+\dfrac{\pi }{6} \right )$

Contestar

amplitud:$3$; periodo:$2\pi $; línea media:$y=0$; sin asíntotas

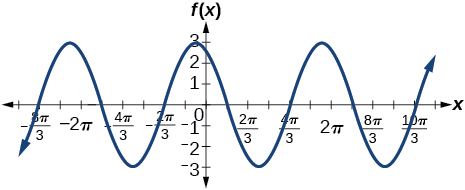
$6R6.1.3.png$

4)$f(x)=-2\sin\left ( x-\dfrac{2\pi }{3} \right )$

5)$f(x)=3\sin\left ( x-\dfrac{\pi }{4} \right )-4$

Contestar

amplitud:$3$; periodo:$2\pi $; línea media:$y=-4$; sin asíntotas

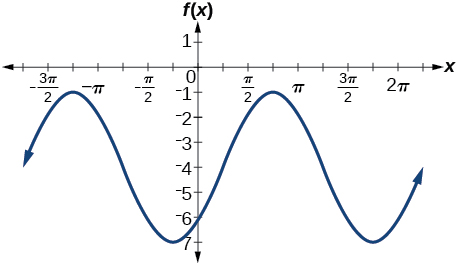
$6R6.1.5.png$

6)$f(x)=2\left (\cos\left ( x-\dfrac{4\pi }{3} \right )+1 \right )$

7)$f(x)=6\sin\left ( 3x-\dfrac{\pi }{6} \right )-1$

Contestar

amplitud:$6$; periodo:$dfrac{2\pi }{3}$; línea media:$y=-1$; sin asíntotas

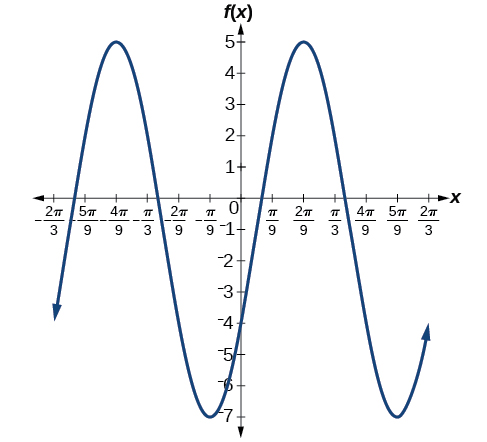
$6R6.1.7.png$

8)$f(x)=-100\sin(50x-20)$

6.2: Gráficas de las Otras Funciones Trigonométricas

Para los ejercicios 1-4, grafica las funciones durante dos periodos y determina el factor de amplitud o estiramiento, el periodo, la ecuación de la línea media y las asíntotas.

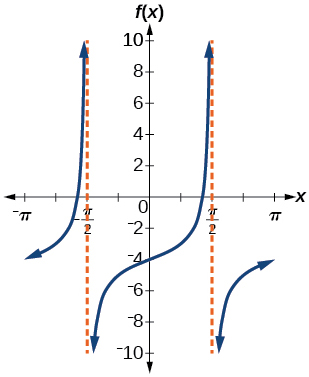
1)$f(x)=\tan x-4$

Contestar

factor de estiramiento: ninguno; periodo:$\pi $; línea media:$y=-4$; asíntotas:$x=\dfrac{\pi }{2}+\pi k$, donde$k$ es un entero

$6R6.2.1.png$

2)$f(x)=2\tan \left ( x-\dfrac{\pi }{6} \right )$

3)$f(x)=-3\tan (4x)-2$

Contestar

factor de estiramiento:$3$; período:$\dfrac{\pi }{4}$; línea media:$y=-2$; asíntotas:$x=\dfrac{\pi }{8}+\dfrac{\pi }{4}k$, donde$k$ es un entero

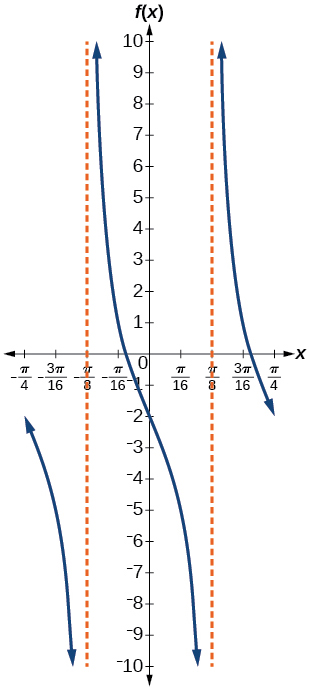
$6R6.2.3.png$

4)$f(x)=0.2\cos(0.1x)+0.3$

Para los ejercicios 5-10, grafica dos periodos completos. Identificar el periodo, el desplazamiento de fase, la amplitud y las asíntotas.

5)$f(x)=\dfrac{1}{3}\sec x$

Contestar

amplitud: ninguno; periodo:$2\pi $; sin desplazamiento de fase; asíntotas:$x=\dfrac{\pi }{2}k$, donde$k$ es un entero

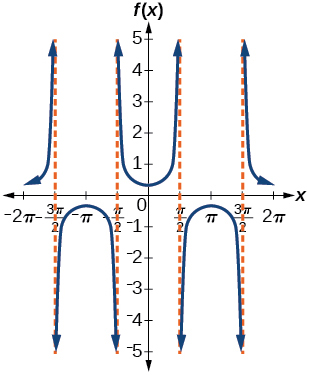
$6R6.2.5.png$

6)$f(x)=3\cot x$

7)$f(x)=4\csc (5x)$

Contestar

amplitud: ninguno; periodo:$\dfrac{2\pi }{5}$; sin desplazamiento de fase; asíntotas:$x=\dfrac{\pi }{5}k$, donde$k$ es un entero

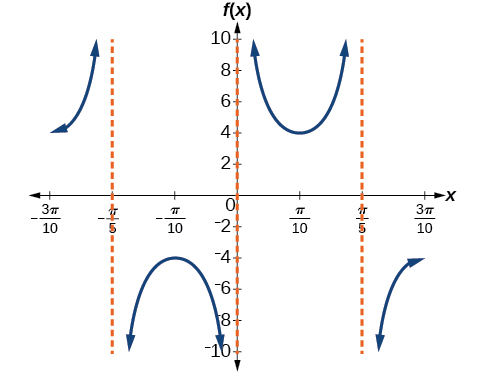
$6R6.2.7.png$

8)$f(x)=8\sec \left (\dfrac{1}{4}x \right )$

9)$f(x)=\dfrac{2}{3}\csc \left (\dfrac{1}{2}x \right )$

Contestar

amplitud: ninguno; periodo:$4\pi $; sin desplazamiento de fase; asíntotas:$x=2\pi k$, donde$k$ es un entero

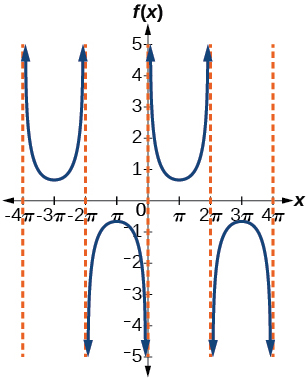
$6R6.2.9.png$

10)$f(x)=-\csc (2x+\pi)$

Para los ejercicios 11-15, utilice este escenario: La población de una ciudad ha subido y bajado en un intervalo de$20$ -año. Su población puede ser modelada por la siguiente función:$y=12,000+8,000\sin(0.628x)$, donde el dominio es los años desde 1980 y el rango es la población de la ciudad.

11) ¿Cuál es la población más grande y más pequeña que pueda tener la ciudad?

Contestar: mayor:$20,000$; más pequeño:$4,000$

12) Graficar la función en el dominio de$[0,40]$.

13) ¿Cuáles son la amplitud, el periodo y el desplazamiento de fase para la función?

Contestar: amplitud:$8,000$; periodo:$10$; desplazamiento de fase:$0$

14) Sobre este dominio, ¿cuándo llega la población$18,000$? $13,000$?

15) ¿Cuál es la población pronosticada en 2007? ¿2010?

Contestar: En 2007, la población pronosticada es$4,413$. En 2010, la población será$11,924$.

Para los ejercicios 16a-16d, supongamos que se une un peso a un resorte y se desplaza hacia arriba y hacia abajo, exhibiendo simetría.

16) Supongamos que la gráfica de la función de desplazamiento se muestra en la Figura siguiente, donde los valores en el$x$ eje -representan el tiempo en segundos y el$y$ eje -representa el desplazamiento en pulgadas.

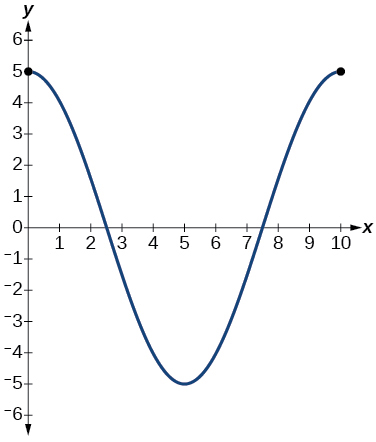
$6R6.2.16.png$

Dar la ecuación que modela el desplazamiento vertical del peso en el muelle.
En$\text{time} = 0$, ¿cuál es el desplazamiento del peso?

Contestar: $5$en.

¿En qué momento el desplazamiento desde el punto de equilibrio es igual a cero?
¿Cuál es el tiempo requerido para que el peso vuelva a su altura inicial de$5$ pulgadas? Es decir, ¿cuál es el periodo para la función de desplazamiento?

Contestar: $10$segundos

6.3: Funciones trigonométricas inversas

Para los ejercicios 1-11, encuentra el valor exacto sin la ayuda de una calculadora.

1)$\sin ^{-1}(1)$

2)$\cos ^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )$

Contestar: $\dfrac{\pi }{6}$

3)$\tan ^{-1}(-1)$

4)$\cos ^{-1}\left ( \dfrac{1}{\sqrt{2}} \right )$

Contestar: $\dfrac{\pi }{4}$

5)$\sin ^{-1}\left ( \dfrac{-\sqrt{3}}{2} \right )$

6)$\sin ^{-1}\left (\cos \left (\dfrac{\pi }{6} \right ) \right )$

Contestar: $\dfrac{\pi }{3}$

7)$\cos ^{-1}\left (\tan \left (\dfrac{3\pi }{4} \right ) \right )$

8)$\sin \left (\sec^{-1} \left (\dfrac{3}{5} \right ) \right )$

Contestar: Sin solución

9)$\cot \left (\sin^{-1} \left (\dfrac{3}{5} \right ) \right )$

10)$\tan \left (\cos^{-1} \left (\dfrac{5}{13} \right ) \right )$

Contestar: $\dfrac{12}{5}$

11)$\sin \left (\cos^{-1} \left (\dfrac{x}{x+1} \right ) \right )$

12) Gráfica$f(x)=\cos x$ y$f(x)=\sec x$ sobre el intervalo$[0,2\pi )$ y explica cualquier observación.

Contestar

Las gráficas no son simétricas con respecto a la línea$y=x$. Son simétricos con respecto al$y$ eje.

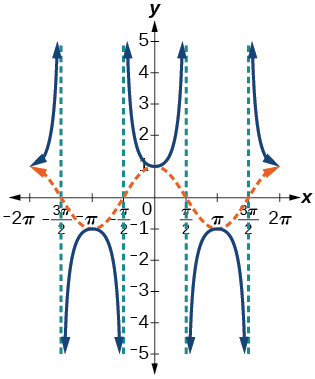
$6R6.3.12.png$

13) Graficar$f(x)=\sin x$$f(x)=\csc x$ y explicar cualquier observación.

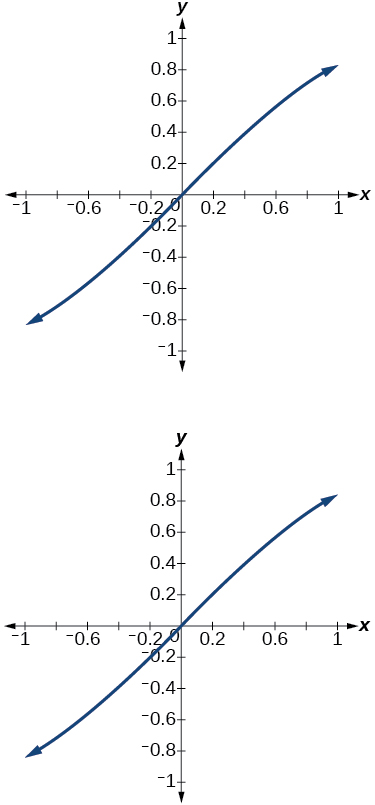
14) Graficar la función$f(x)=\dfrac{x}{1}-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}$ en el intervalo$[-1,1]$ y comparar la gráfica con la gráfica de$f(x)=\sin x$ en el mismo intervalo. Describir cualquier observación.

Contestar

Las gráficas parecen ser idénticas.

$6R6.3.14.png$

Prueba de práctica

Para los ejercicios 1-13, bosquejar la gráfica de cada función durante dos periodos completos. Determinar la amplitud, el periodo y la ecuación para la línea media.

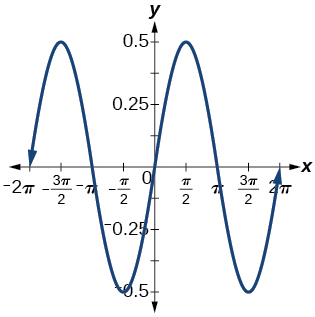
1)$f(x)=0.5\sin x$

Contestar

amplitud:$0.5$; periodo:$2\pi $; línea media$y=0$

$6RP 1.png$ $  y = 0   " role="presentation" style="background-color:transparent;border-bottom-color:rgb(85, 85, 85);border-bottom-style:none;border-bottom-width:0px;border-image-outset:0;border-image-repeat:stretch;border-image-slice:100%;border-image-source:none;border-image-width:1;border-left-color:rgb(85, 85, 85);border-left-style:none;border-left-width:0px;border-right-color:rgb(85, 85, 85);border-right-style:none;border-right-width:0px;border-top-color:rgb(85, 85, 85);border-top-style:none;border-top-width:0px;box-sizing:border-box;direction:ltr;display:inline;float:none;font-family:Helvetica Neue,Helvetica,Arial,sans-serif;font-size-adjust:none;font-style:normal;font-variant:normal;font-weight:400;letter-spacing:normal;line-height:normal;margin-bottom:0px;margin-left:0px;margin-right:0px;margin-top:0px;max-height:none;max-width:none;min-height:0px;min-width:0px;orphans:2;padding-bottom:0px;padding-left:0px;padding-right:0px;padding-top:0px;position:relative;text-align:left;text-decoration:none;text-indent:0px;text-transform:none;-webkit-text-stroke-width:0px;white-space:nowrap;word-spacing:0px;word-wrap:normal;" tabindex="0">$ y = 0 y=0 y=0

2)$f(x)=5\cos x$

3)$f(x)=5\sin x$

Contestar

amplitud:$0.5$; periodo:$2\pi $; línea media$y=0$

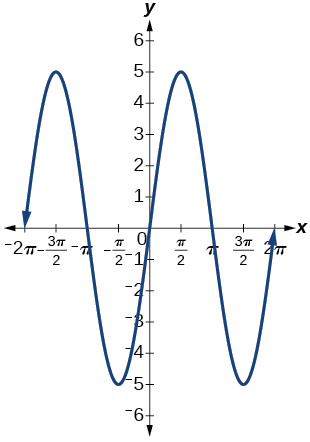
$6RP 3.png$

4)$f(x)=\sin (3x)$

5)$f(x)=-\cos \left ( x+\dfrac{\pi }{3} \right )+1$

Contestar

amplitud:$1$; periodo:$2\pi $; línea media$y=1$

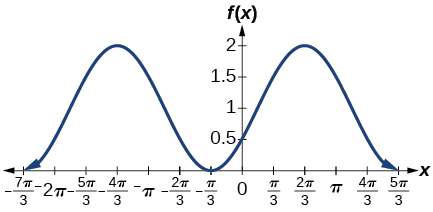
$6RP 5.png$

6)$f(x)=5\sin \left (3\left ( x-\dfrac{\pi }{6} \right ) \right )+4$

7)$f(x)=3\cos \left ( \dfrac{1}{3}x-\dfrac{5\pi }{6} \right )$

Contestar

amplitud:$3$; periodo:$6\pi $; línea media$y=0$

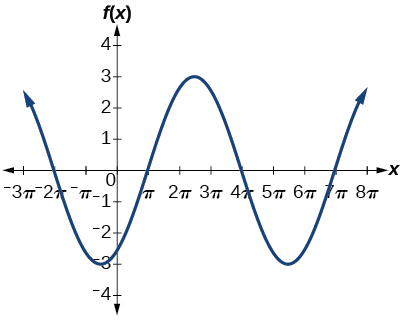
$6RP 7.png$

8)$f(x)=\tan (4x)$

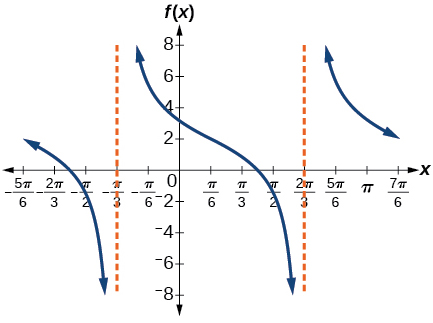
9)$f(x)=-2\tan \left ( x-\dfrac{7\pi }{6} \right )+2$

Contestar

amplitud: ninguna; periodo:$\pi $; línea media$y=0$, asíntotas:$x=\dfrac{2\pi }{3}+\pi k$,donde$k$ es un entero

$6RP 9.png$

10)$f(x)=\pi \cos(3x+\pi)$

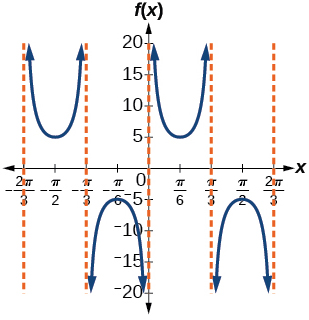
11)$f(x)=5\csc(3x)$

Contestar

amplitud: ninguna; periodo:$\dfrac{2\pi }{3}$; línea media$y=0$, asíntotas:$x=\dfrac{\pi }{3}k$,donde$k$ es un entero

$6RP 11.png$

12)$f(x)=\pi \sec \left ( \dfrac{\pi }{2}x \right )$

13)$f(x)=2\csc \left ( x+\dfrac{\pi }{4} \right )-3$

Contestar

amplitud: ninguna; periodo:$2\pi $; línea media$y=-3$

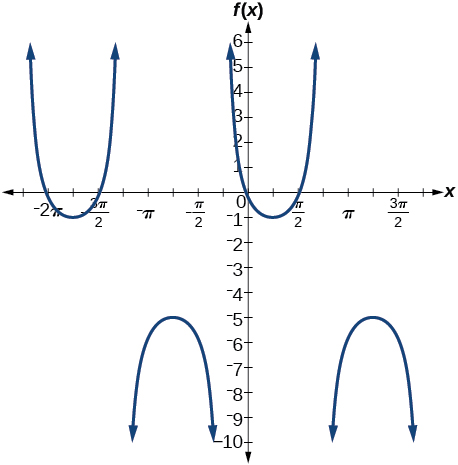
$6RP 13.png$

Para los ejercicios 14-16, determine la amplitud, el punto y la línea media de la gráfica, y luego busque una fórmula para la función.

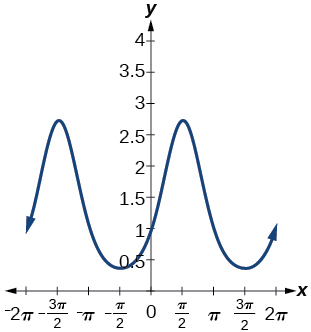
14) Dar en términos de una función sinusoidal.

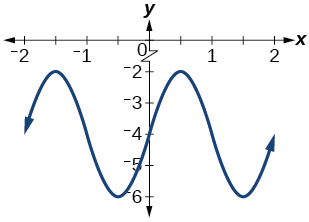
$6RP 14.png$

15) Dar en términos de una función sinusoidal.

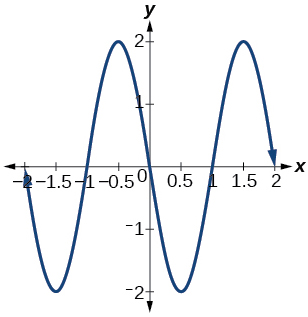
$6RP 15.png$

Contestar: amplitud:$2$; periodo:$2$; línea media:$y=0$;$f(x)=2\sin(\pi (x-1))$

16) Dar en términos de una función tangente.

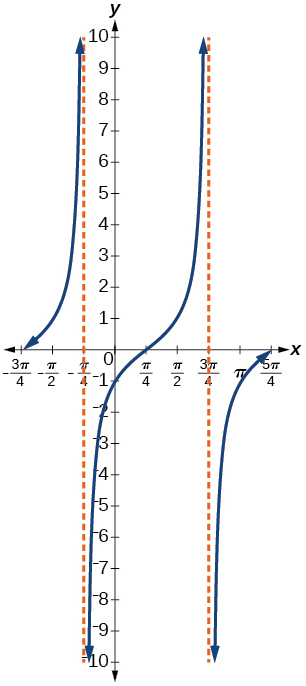
$6RP 16.png$

Para los ejercicios 17-20, encuentra la amplitud, el periodo, el desplazamiento de fase y la línea media.

17)$y=\sin\left(\dfrac{\pi}{6}x+\pi \right)-3$

Contestar: amplitud:$1$; periodo:$12$; desplazamiento de fase:$-6$; línea media:$y=-3$

18)$y=8\sin\left(\dfrac{7\pi}{6}x+\dfrac{7\pi}{2} \right)+6$

19) La temperatura exterior en el transcurso de un día se puede modelar como una función sinusoidal. Supongamos que sabe que la temperatura es$68^{\circ}$ F a medianoche y las temperaturas altas y bajas durante el día son$80^{\circ}$ F y$56^{\circ}$ F, respectivamente. Asumiendo$t$ es el número de horas desde la medianoche, encontrar una función para la temperatura$D$,, en términos de$t$.

Contestar: $D(t)=68-12\sin\left(\dfrac{\pi}{12}x \right)$

20) El agua se bombea a un contenedor de almacenamiento y se vacía de acuerdo a una tasa periódica. La profundidad del agua es$3$ pies en su punto más bajo a las 2:00 a.m. y$71$ pies en su nivel más alto, lo que ocurre cada$5$ hora. Escribe una función coseno que modele la profundidad del agua en función del tiempo, y luego grafica la función por un periodo.

Para los ejercicios 21-25, encuentra el periodo y el desplazamiento horizontal de cada función.

21)$g(x)=3\tan(6x+42)$

Contestar: periodo:$\dfrac{\pi}{6}$; desplazamiento horizontal:$-7$

22)$n(x)=4\csc \left(\dfrac{5\pi }{3}x-\dfrac{20\pi }{3} \right)$

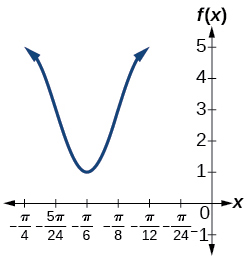
23) Escribir la ecuación para la gráfica en la Figura siguiente en términos de la función secante y dar el periodo y el desplazamiento de fase.

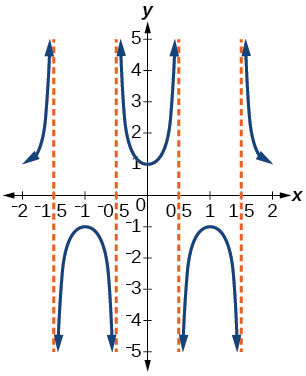
$6RP 23.png$

Contestar: $f(x)=\sec(\pi x)$; periodo:$2$; desplazamiento de fase:$0$

24) Si$\tan x=3$, encontrar$\tan (-x)$.

25) Si$\sec x=4$, encuentra$\sec (-x)$.

Contestar: $4$

Para los ejercicios 26-28, grafica las funciones en la ventana especificada y responde las preguntas.

26) Gráfica$m(x)=\sin(2x)+\cos(3x)$ en la ventana de visualización$[-10,10]$ por$[-3,3]$. Aproximar el periodo de la gráfica.

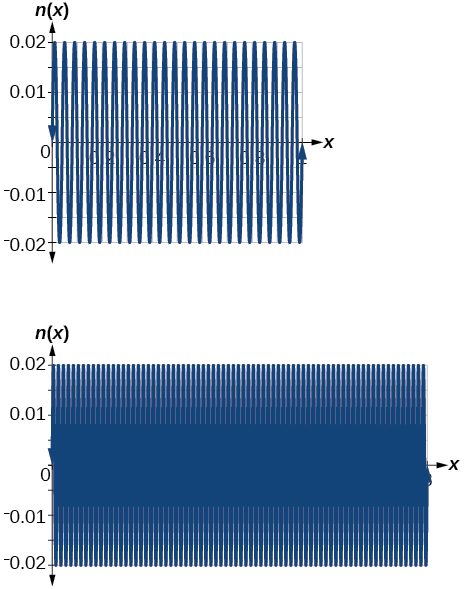
27) Gráfica$n(x)=0.02\sin(50\pi x)$ sobre los siguientes dominios en$x:[0,1]$ y$[0,3]$. Supongamos que esta función modela ondas sonoras. ¿Por qué estas vistas se verían tan diferentes?

Contestar

Las vistas son diferentes porque el periodo de la ola es$125$. Sobre un dominio más grande, habrá más ciclos de la gráfica.

$6RP 27.png$

28)$f(x)=\dfrac{\sin x}{x}$ Grafique$[-0.5,0.5]$ y explique cualquier observación.

Para los ejercicios 29-31, vamos$f(x)=\dfrac{3}{5}\cos(6x)$.

29) ¿Cuál es el mayor valor posible$f(x)$?

Contestar: $\dfrac{3}{5}$

30) ¿Cuál es el valor más pequeño posible$f(x)$?

31) ¿Dónde aumenta la función en el intervalo$[0,2\pi ]$?

Contestar: En los intervalos aproximados$(0.5,1),(1.6,2.1),(2.6,3.1),(3.7,4.2),(4.7,5.2),(5.6,6.28)$

Para los ejercicios 32-33, busque y grafique un periodo de la función periódica con la amplitud, periodo y desplazamiento de fase dados.

32) Curva sinusoidal con amplitud$3$, periodo$\dfrac{\pi }{3}$, y desplazamiento de fase$(h,k)=\left(\dfrac{\pi }{4},2\right)$

33) Curva coseno con amplitud$2$, periodo$\dfrac{\pi }{6}$, y desplazamiento de fase$(h,k)=\left(-\dfrac{\pi }{4},3\right)$

Contestar

$f(x)=2\cos\left ( 12\left ( x+\dfrac{\pi }{4} \right ) \right )+3$

$6RP 33.png$

Para los ejercicios 34-35, grafica la función. Describir la gráfica y, en su caso, cualquier comportamiento periódico, amplitud, asíntotas o puntos indefinidos.

34)$f(x)=5\cos(3x)+4\sin(2x)$

35)$f(x)=e^{(sint)}$

Contestar

Esta gráfica es periódica con un periodo de$2\pi $

$6RP 35.png$

Para los ejercicios 36-43, encuentra el valor exacto.

36)$\sin^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )$

37)$\tan^{-1}\left ( \sqrt{3} \right )$

Contestar: $\dfrac{\pi }{3}$

38)$\cos^{-1}\left ( -\dfrac{\sqrt{3}}{2} \right )$

39)$\cos^{-1}\left ( \sin(\pi) \right )$

Contestar: $\dfrac{\pi }{2}$

40)$\cos^{-1}\left ( \tan \left (\dfrac{7\pi}{4} \right ) \right )$

41)$\cos(\sin^{-1}(1-2x))$

Contestar: $\sqrt{1-(1-2x)^2}$

42)$\cos^{-1}(-0.4)$

43)$\cos \left (\tan^{-1}\left(x^2\right) \right )$

Contestar: $\dfrac{1}{\sqrt{1+x^4}}$

Para los ejercicios 44-46, supongamos$\sin t=\dfrac{x}{x+1}$. Evalúe las siguientes expresiones.

44)$\tan t$

45)$csc t$

Contestar: $\dfrac{x+1}{x}$

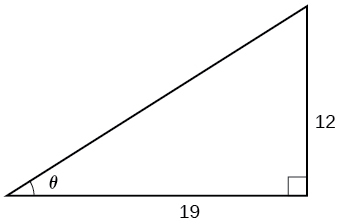
46) Dada la Figura, encontrar la medida del ángulo$\theta $ a tres decimales. Contesta en radianes.

$6RP 46.png$

Para los ejercicios 47-49, determinar si la ecuación es verdadera o falsa.

47)$\arcsin\left(\sin\left(\dfrac{5\pi }{6}\right)\right)=\dfrac{5\pi }{6}$

Contestar: Falso

48)$\arccos\left(\cos\left(\dfrac{5\pi }{6}\right)\right)=\dfrac{5\pi }{6}$

49) El grado de una carretera es$7\%$. Esto significa que por cada distancia horizontal de$100$ pies en la carretera, el ascenso vertical es$7$ pies. Encuentra el ángulo que hace la carretera con la horizontal en radianes.

Contestar: aproximadamente$0.07$ radianes

Search

Text Color

Text Size

Margin Size

Font Type

6.2: Gráficas de las Otras Funciones Trigonométricas

6.3: Funciones trigonométricas inversas

Prueba de práctica