8.2: Triángulos no rectos - Ley de Cosinos
- Page ID
- 121251
En esta sección, usted:
- Utilizar la Ley de Cosinos para resolver triángulos oblicuos.
- Resolver problemas aplicados utilizando la Ley de Cosinos.
- Usa la fórmula de Heron para encontrar el área de un triángulo.
Supongamos que una embarcación sale de puerto, recorre\(10\) millas, gira\(20\) grados y recorre otras 8 millas como se muestra en la Figura\(\PageIndex{1}\) ¿A qué distancia del puerto está la embarcación?
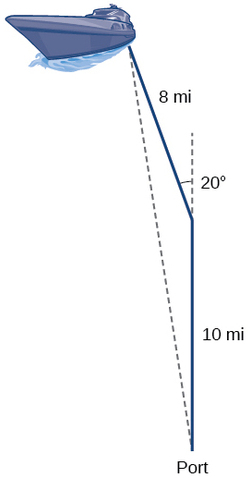
Figura\(\PageIndex{1}\)
Desafortunadamente, si bien la Ley de Sines nos permite abordar muchos casos que no son triangulares rectos, no nos ayuda con triángulos donde el ángulo conocido está entre dos lados conocidos, un triángulo SAS (lado-ángulo-lado), o cuando se conocen los tres lados, pero no se conocen ángulos, un triángulo SSS (lado-lado-lado). En esta sección, investigaremos otra herramienta para resolver triángulos oblicuos descritos por estos dos últimos casos.
Uso de la Ley de los Cosinos para Resolver Triángulos Oblicua
La herramienta que necesitamos para resolver el problema de la distancia de la embarcación al puerto es la Ley de Cosinos, que define la relación entre las medidas de ángulo y longitudes laterales en triángulos oblicuos. Tres fórmulas conforman la Ley de los Cosinos. A primera vista, las fórmulas pueden parecer complicadas porque incluyen muchas variables. Sin embargo, una vez que se entiende el patrón, la Ley de Cosinos es más fácil de trabajar que la mayoría de las fórmulas en este nivel matemático.
Comprender cómo se deriva la Ley de Cosinos será útil en el uso de las fórmulas. La derivación comienza con el Teorema Generalizado de Pitágoras, que es una extensión del Teorema de Pitágoras a triángulos no rectos. Así es como funciona: Un triángulo arbitrario no recto\(ABC\) se coloca en el plano de coordenadas con vértice\(A\) en el origen, lado\(c\) dibujado a lo largo del eje x, y vértice\(C\) ubicado\((x,y)\) en algún punto del plano, como se ilustra en la Figura\(\PageIndex{2}\). Generalmente, los triángulos existen en cualquier parte del plano, pero para esta explicación colocaremos el triángulo como se señaló.
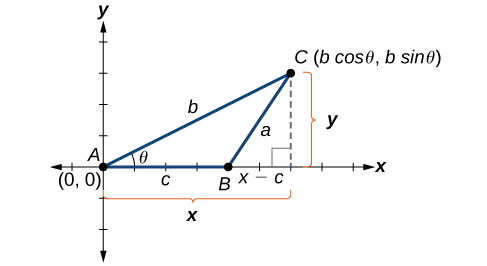
Figura\(\PageIndex{2}\)
Podemos dejar caer una\(C\) perpendicular desde el eje x (esta es la altitud o altura). Recordando las identidades trigonométricas básicas, sabemos que
\(\cos \theta=\dfrac{x(adjacent)}{b(hypotenuse)}\)y\(\sin \theta=\dfrac{y(opposite)}{b(hypotenuse)}\)
En términos de\(\theta\),\(x=b \cos \theta\) y\(y=b \sin \theta\). El\((x,y)\) punto ubicado en\(C\) tiene coordenadas\((b \cos \theta, b \sin \theta)\). Usando el lado\((x−c)\) como una pata de un triángulo rectángulo y\(y\) como el segundo tramo, podemos encontrar la longitud de la hipotenusa\(a\) usando el Teorema de Pitágoras. Así,
\ (\ begin {array} {ll} a^2= {(x−c)} ^2+y^2\\ [4pt]\;\;\;\;\;\; = {(b\ cos\ theta−c)} ^2+ {(b\ sin\ theta)} ^2 &\ text {Sustituir} (b\ cos\ theta)\ text {para} x\ texto y {} (b\ sin\ theta)\ text {for} y\\ [4pt]\;\;\;\;\;\;\; = (b^2 {\ cos} ^2\ theta−2bc\ cos\ theta+c^2) +b^2 {\ sin} ^2\ theta &\ text {Expandir el perfecto cuadrado.}\\\ [4pt]\;\;\;\; = b^2 {\ cos} ^2\ theta+b^2 {\ sin} ^2\ theta+c^2−2bc\ cos\ theta &\ text {Términos de grupo señalando que} {\ cos} ^2\ theta+ {\ sin} ^2\ theta=1\ [4pt]\;\;\;\;\; =b^2 ({\ cos} ^2\ theta+ {\ sin} ^2\ theta) +c^2−2bc\ cos\ theta &\ text {Factor de salida} b^2\\ [4pt]
a^2=b^2+c^2−2bc\ cos\ theta \ end {array}\)
La fórmula derivada es una de las tres ecuaciones de la Ley de Cosinos. Las otras ecuaciones se encuentran de manera similar.
Ten en cuenta que siempre es útil bosquejar el triángulo a la hora de resolver ángulos o lados. En un escenario del mundo real, intenta dibujar un diagrama de la situación. A medida que surja más información, el diagrama puede tener que ser alterado. Realiza esas alteraciones al diagrama y, al final, el problema será más fácil de resolver.
La Ley de Cosinos establece que el cuadrado de cualquier lado de un triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble del producto de los otros dos lados y el coseno del ángulo incluido.
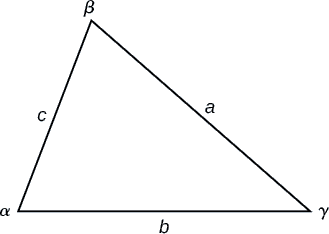
Figura\(\PageIndex{3}\)
Para los triángulos etiquetados como en la Figura\(\PageIndex{3}\)\(\alpha\), con ángulos\(\gamma\),\(\beta\) y lados correspondientes opuestos\(a\)\(b\),, y\(c\), respectivamente, la Ley de Cosinos se da como tres ecuaciones.
\[a^2=b^2+c^2−2bc \cos \alpha\]
\[b^2=a^2+c^2−2ac \cos \beta\]
\[c^2=a^2+b^2−2ab \cos \gamma\]
Para resolver una medición lateral faltante, se necesita la medida de ángulo opuesto correspondiente.
Al resolver un ángulo, se necesita la medida lateral opuesta correspondiente. Podemos usar otra versión de la Ley de Cosinos para resolver por un ángulo.
\[\cos \alpha=\dfrac{b^2+c^2−a^2}{2bc}\]
\[\cos \beta=\dfrac{a^2+c^2−b^2}{2ac}\]
\[\cos \gamma=\dfrac{a^2+b^2−c^2}{2ab}\]
- Esboza el triángulo. Identificar las medidas de los lados y ángulos conocidos. Utilizar variables para representar las medidas de los lados y ángulos desconocidos.
- Aplicar la Ley de Cosinos para encontrar la longitud del lado o ángulo desconocido.
- Aplicar la Ley de Sinos o Cosinos para encontrar la medida de un segundo ángulo.
- Calcular la medida del ángulo restante.
Encuentra el lado desconocido y los ángulos del triángulo en la Figura\(\PageIndex{4}\).
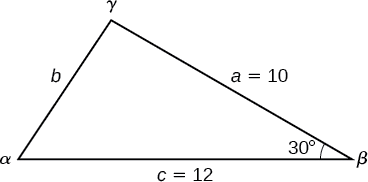
Figura\(\PageIndex{4}\)
Solución
Primero, toma nota de lo que se da: dos lados y el ángulo entre ellos. Este arreglo se clasifica como SAS y suministra los datos necesarios para aplicar la Ley de Cosinos.
Cada una de las tres leyes de los cosenos comienza con el cuadrado de un lado desconocido opuesto a un ángulo conocido. Para este ejemplo, el primer lado a resolver es lado\(b\), como conocemos la medición del ángulo opuesto\(\beta\).
\(\begin{array}{ll} b^2=a^2+c^2−2ac \cos \beta \\[4pt] b^2={10}^2+{12}^2−2(10)(12)\cos(30°) & \text{Substitute the measurements for the known quantities.} \\[4pt] b^2=100+144−240 \left(\dfrac{\sqrt{3}}{2}\right) & \text{Evaluate the cosine and begin to simplify.} \\[4pt] b^2=244−120\sqrt{3} \\[4pt] b=\sqrt{244−120\sqrt{3}} & \text{Use the square root property.} \\[4pt] b≈6.013 \end{array}\)
Debido a que estamos resolviendo para una longitud, usamos solo la raíz cuadrada positiva. Ahora que conocemos la longitud\(b\), podemos usar la Ley de los Sinos para rellenar los ángulos restantes del triángulo. Resolviendo para ángulo\(\alpha\), tenemos
\(\begin{array}{cc} \dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b} \\[4pt] \dfrac{\sin \alpha}{10}=\dfrac{\sin(30°)}{6.013} \\[4pt] \sin \alpha=\dfrac{10\sin(30°)}{6.013} & \text{Multiply both sides of the equation by }10. \\[4pt] \alpha={\sin}^{−1}\left(\dfrac{10\sin(30°)}{6.013}\right) & \text{Find the inverse sine of } \dfrac{10\sin(30°)}{6.013}. \\[4pt] \alpha≈56.3° \end{array}\)
La otra posibilidad para\(\alpha\) sería\(\alpha=180°-56.3°≈123.7°\). En el diagrama original,\(\alpha\) es adyacente al lado más largo, por lo que\(\alpha\) es un ángulo agudo y, por lo tanto,\(123.7°\) no tiene sentido. Observe que si elegimos aplicar la Ley de Cosinos, llegamos a una respuesta única. No tenemos que considerar las otras posibilidades, ya que el coseno es único para los ángulos entre\(0°\) y\(180°\). Procediendo con\(\alpha≈56.3°\), entonces podemos encontrar el tercer ángulo del triángulo.
\[\begin{align*} \gamma&= 180^{\circ}-30^{\circ}-56.3^{\circ}\\ &\approx 93.7^{\circ} \end{align*}\]
El conjunto completo de ángulos y lados es
\(\alpha≈56.3°\)\(a=10\)
\(\beta=30°\)\(b≈6.013\)
\(\gamma≈93.7°\)\(c=12\)
Encuentra el lado faltante y los ángulos del triángulo dado:\(\alpha=30°\),\(b=12\),\(c=24\).
- Responder
-
\(a≈14.9\),\(\beta≈23.8°\),\(\gamma≈126.2°\).
Encuentra el ángulo\(\alpha\) para el triángulo dado si es lado\(a=20\)\(b=25\), lado y lado\(c=18\).
Solución
Para este ejemplo, no tenemos ángulos. Podemos resolver para cualquier ángulo utilizando la Ley de Cosinos. Para resolver por ángulo\(\alpha\), tenemos
\(\begin{array}{ll} a^2=b^2+c^2−2bc \cos \alpha \\[4pt] {20}^2={25}^2+{18}^2−2(25)(18)\cos \alpha & \text{Substitute the appropriate measurements.} \\[4pt] 400=625+324−900 \cos \alpha & \text{ Simplify in each step.} \\[4pt] 400=949−900 \cos \alpha \\[4pt] −549=−900 \cos \alpha & \text{Isolate }\cos \alpha. \\[4pt] 0.61≈\cos \alpha & \text{Find the inverse cosine.} \\[4pt] \alpha≈52.4° \end{array}\)
Ver Figura\(\PageIndex{5}\).
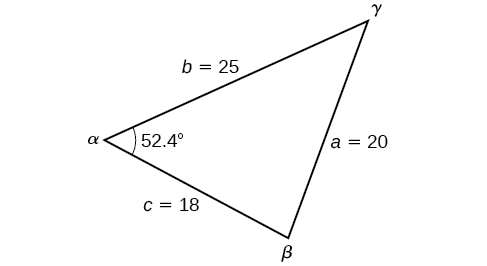
Figura\(\PageIndex{5}\)
Análisis
Debido a que el coseno inverso puede devolver cualquier ángulo entre\(0\) y\(180\) grados, no habrá ningún caso ambiguo usando este método.
Dado\(a=5\),\(b=7\), y\(c=10\), encontrar los ángulos faltantes.
- Responder
-
\(\alpha≈27.7°\),\(\beta≈40.5°\),\(\gamma≈111.8°\)
Resolviendo Problemas Aplicados Utilizando la Ley de Cosinos
Así como la Ley de Sines proporcionó las ecuaciones adecuadas para resolver una serie de aplicaciones, la Ley de Cosinos es aplicable a situaciones en las que los datos dados se ajusten a los modelos cosenales. Podemos verlas en los campos de la navegación, la topografía, la astronomía y la geometría, solo por nombrar algunos.
En muchos celulares con GPS, se puede dar una ubicación aproximada antes de recibir la señal GPS. Esto se logra a través de un proceso llamado triangulación, que funciona utilizando las distancias desde dos puntos conocidos. Supongamos que hay dos torres de telefonía celular dentro del alcance de un celular. Las dos torres se encuentran a\(6000\) pies de distancia a lo largo de una carretera recta, que corre de este a oeste, y el celular se encuentra al norte de la carretera. Con base en el retardo de la señal, se puede determinar que la señal está a\(5050\) pies de la primera torre y\(2420\) pies de la segunda torre. Determinar la posición del celular al norte y al este de la primera torre, y determinar qué tan lejos está de la carretera.
Solución
Para simplificar, comenzamos dibujando un diagrama similar a Figura\(\PageIndex{6}\) y etiquetando nuestra información dada.
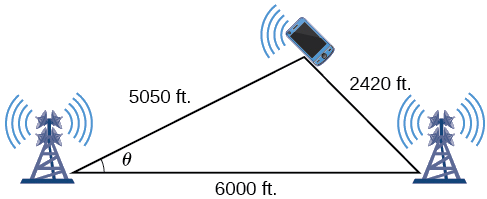
Figura\(\PageIndex{6}\)
Usando la Ley de Cosinos, podemos resolver para el ángulo\(\theta\). Recuerda que la Ley de Cosinos utiliza el cuadrado de un lado para encontrar el coseno del ángulo opuesto. Para este ejemplo, vamos\(a=2420\),\(b=5050\), y\(c=6000\). Así,\(\theta\) corresponde al lado opuesto\(a=2420\).
\[\begin{align*} a^2 & =b^2+c^2−2bc \cos \theta \\[4pt] {(2420)}^2 &={(5050)}^2+{(6000)}^2−2(5050)(6000) \cos \theta \\[4pt] \cos \theta &≈ 0.9183 \\[4pt] \theta &≈ {\cos}^{−1}(0.9183) \\[4pt] \theta &≈ 23.3° \end{align*}\]
Para responder a las preguntas sobre la posición del teléfono al norte y al este de la torre, y la distancia a la autopista, baje una perpendicular desde la posición del celular, como en la Figura\(\PageIndex{7}\). Esto forma dos triángulos rectos, aunque solo necesitamos el triángulo rectángulo que incluye la primera torre para este problema.
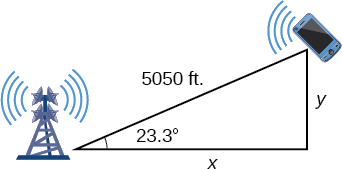
Figura\(\PageIndex{7}\)
Usando el ángulo\(\theta=23.3\)° y las identidades trigonométricas básicas, podemos encontrar las soluciones. Así
\[\begin{align*} \cos(23.3°) &= \dfrac{x}{5050} \\[4pt] x &= 5050\cos(23.3°) \\[4pt] x &≈ 4638.15\, feet\\[4pt] \sin(23.3°) &= \dfrac{y}{5050} \\[4pt] y &= 5050\sin(23.3°) \\[4pt] y &≈1997.5 \, feet \end{align*}\]
El celular está aproximadamente\(4638\) pies al este y\(1998\) pies al norte de la primera torre, y a\(1998\) pies de la carretera.
Volviendo a nuestro problema al inicio de esta sección, supongamos que una embarcación sale de puerto, recorre\(10\) millas, gira\(20\) grados y recorre otras\(8\) millas. ¿A qué distancia del puerto está el barco? El diagrama se repite aquí en la Figura\(\PageIndex{8}\).
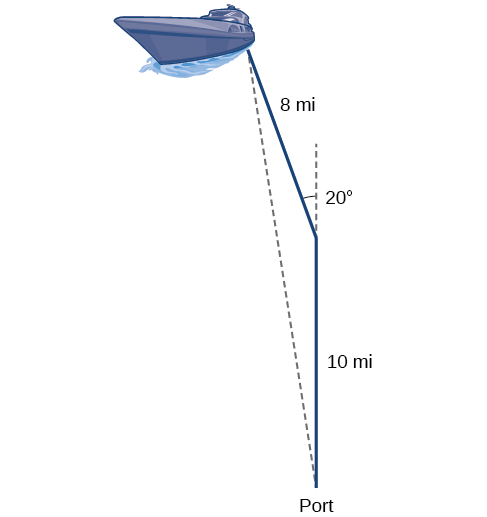
Figura\(\PageIndex{8}\)
Solución
El barco giró 20 grados, por lo que el ángulo obtuso del triángulo no recto es el ángulo suplementario,\(180°−20°=160°\). Con esto, podemos utilizar la Ley de Cosines para encontrar el lado faltante del triángulo obtuso: la distancia de la embarcación hasta el puerto.
\[\begin{align*} x^2 &= 8^2+{10}^2−2(8)(10)\cos(160°) \\[4pt] x^2 &= 314.35 \\[4pt] x &= \sqrt{314.35} \\[4pt] x&≈17.7\, miles \end{align*}\]
El barco está\(17.7\) a unos kilómetros del puerto.
Usando la fórmula de Heron para encontrar el área de un triángulo
Ya aprendimos a encontrar el área de un triángulo oblicuo cuando conocemos dos lados y un ángulo. También conocemos la fórmula para encontrar el área de un triángulo usando la base y la altura. Cuando conocemos los tres lados, sin embargo, podemos usar la fórmula de Heron en lugar de encontrar la altura. Garza de Alejandría fue un geómetro que vivió durante el siglo I d.C. Descubrió una fórmula para encontrar el área de triángulos oblicuos cuando se conocen tres lados.
La fórmula de Heron encuentra el área de triángulos oblicuos en los que\(c\) se conocen los lados\(a\)\(b\),, y.
\[Area=\sqrt{s(s−a)(s−b)(s−c)}\]
donde\(s=\dfrac{(a+b+c)}{2}\) se encuentra la mitad del perímetro del triángulo, a veces llamado el semiperímetro.
Encuentra el área del triángulo en Figura\(\PageIndex{9}\) usando la fórmula de Heron.
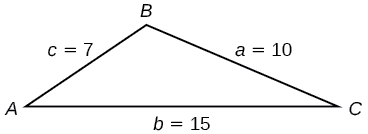
Figura\(\PageIndex{9}\)
Solución
Primero, calculamos\(s\).
\[\begin{align*} s&= \dfrac{(a+b+c)}{2}\\ s&= \dfrac{(10+15+7)}{2}\\ &= 16 \end{align*}\]
Después aplicamos la fórmula.
\[\begin{align*} Area&= \sqrt{s(s-a)(s-b)(s-c)}\\ Area&= \sqrt{16(16-10)(16-15)(16-7)}\\ Area&\approx 29.4 \end{align*}\]
El área es aproximadamente de unidades\(29.4\) cuadradas.
Usa la fórmula de Heron para encontrar el área de un triángulo con lados de longitudes\(a=29.7\)\(b=42.3\) pies, pies y\(c=38.4\) pies.
- Responder
-
Área = pies\(552\) cuadrados
Un desarrollador de la ciudad de Chicago quiere construir un edificio compuesto por lofts de artistas en un lote triangular bordeado por Rush Street, Wabash Avenue y Pearson Street. El frente a lo largo de Rush Street es de aproximadamente\(62.4\) metros, a lo largo de la avenida Wabash es de aproximadamente\(43.5\) metros, y a lo largo de la calle Pearson es aproximadamente\(34.1\) metros. ¿Cuántos metros cuadrados están disponibles para el desarrollador? Ver Figura\(\PageIndex{10}\) para una vista de la propiedad de la ciudad.
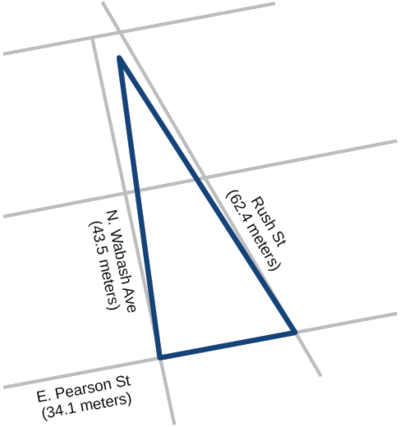
Figura\(\PageIndex{10}\)
Solución
Encuentra la medida para\(s\), que es la mitad del perímetro.
\[\begin{align*} s&= \dfrac{(62.4+43.5+34.1)}{2}\\ s&= 70\; m\\ \text {Apply Heron's formula.}\\ Area&= \sqrt{70(70-62.4)(70-43.5)(70-34.1)}\\ Area&= \sqrt{506,118.2}\\ Area&\approx 711.4 \end{align*}\]
El desarrollador cuenta con unos metros\(711.4\) cuadrados.
Encuentra el área de un triángulo dado\(a=4.38\) pies,\(b=3.79\) pies y\(c=5.22\) pies.
- Responder
-
aproximadamente pies\(8.15\) cuadrados
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con la Ley de Cosinos.
Ecuaciones Clave
| Ley de Cosinos |
\(a^2=b^2+c^2−2bc \cos \alpha\) \(b^2=a^2+c^2−2ac \cos \beta\) \(c^2=a^2+b^2−2ab \cos \gamma\) |
| Fórmula de Heron |
\(Area=\sqrt{s(s−a)(s−b)(s−c)}\) donde\(s=\dfrac{(a+b+c)}{2}\) |
Conceptos clave
- La Ley de Cosinos define la relación entre las medidas de ángulo y longitudes de lados en triángulos oblicuos.
- El Teorema Generalizado de Pitágoras es la Ley de Cosinos para dos casos de triángulos oblicuos: SAS y SSS. Al soltar una perpendicular imaginaria se divide el triángulo oblicuo en dos triángulos rectos o se forma un triángulo rectángulo, lo que permite relacionar los lados y calcular las mediciones. Ver Ejemplo\(\PageIndex{1}\) y Ejemplo\(\PageIndex{2}\).
- La Ley de Cosinos es útil para muchos tipos de problemas aplicados. El primer paso para resolver este tipo de problemas es generalmente dibujar un boceto del problema presentado. Si la información dada se ajusta a uno de los tres modelos (las tres ecuaciones), entonces aplicar la Ley de Cosinos para encontrar una solución. Ver Ejemplo\(\PageIndex{3}\) y Ejemplo\(\PageIndex{4}\).
- La fórmula de Heron permite calcular el área en triángulos oblicuos. Deben conocerse los tres lados para aplicar la fórmula de Heron. Ver Ejemplo\(\PageIndex{5}\) y Ver Ejemplo\(\PageIndex{6}\).


