8.1: Triángulos no rectos - Ley de los senos
- Page ID
- 121195
- Usa la Ley de Sines para resolver triángulos oblicuos.
- Encuentra el área de un triángulo oblicuo usando la función seno.
- Resolver problemas aplicados utilizando la Ley de Sines.
Supongamos que dos estaciones de radar ubicadas\(20\) a millas de distancia cada una detectan una aeronave entre ellas El ángulo de elevación medido por la primera estación es\(35\) grados, mientras que el ángulo de elevación medido por la segunda estación es\(15\) grados. ¿Cómo podemos determinar la altitud de la aeronave? Vemos en Figura\(\PageIndex{1}\) que el triángulo formado por la aeronave y las dos estaciones no es un triángulo rectángulo, por lo que no podemos usar lo que sabemos de los triángulos rectos. En esta sección, descubriremos cómo resolver problemas que involucran triángulos no rectos.
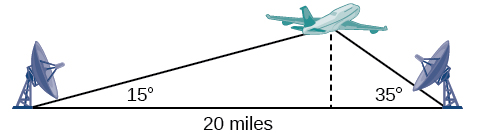
Figura\(\PageIndex{1}\)
Uso de la Ley de los Senos para Resolver Triángulos Obliques
En cualquier triángulo, podemos dibujar una altitud, una línea perpendicular desde un vértice al lado opuesto, formando dos triángulos rectos. Sería preferible, sin embargo, tener métodos que podamos aplicar directamente a triángulos no rectos sin antes tener que crear triángulos rectos.
Cualquier triángulo que no sea un triángulo rectángulo es un triángulo oblicuo. Resolver un triángulo oblicuo significa encontrar las medidas de los tres ángulos y los tres lados. Para ello, necesitamos comenzar con al menos tres de estos valores, incluyendo al menos uno de los lados. Investigaremos tres posibles situaciones problemáticas de triángulo oblicuo:
ASA (ángulo-lado-ángulo) Conocemos las medidas de dos ángulos y el lado incluido. Ver Figura\(\PageIndex{2}\).
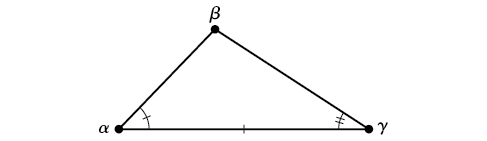
Figura\(\PageIndex{2}\)
AAS (ángulo-ángulo-lado) Conocemos las medidas de dos ángulos y un lado que no está entre los ángulos conocidos. Ver Figura\(\PageIndex{3}\).
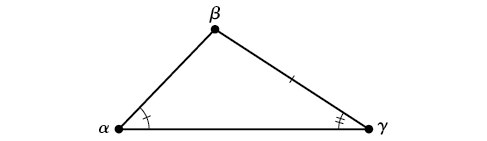
Figura\(\PageIndex{3}\)
SSA (lado-lado-ángulo) Conocemos las medidas de dos lados y un ángulo que no está entre los lados conocidos. Ver Figura\(\PageIndex{4}\).
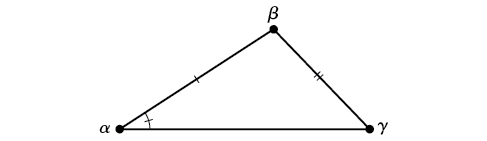
Figura\(\PageIndex{4}\)
Saber abordar cada una de estas situaciones nos permite resolver triángulos oblicuos sin tener que soltar una perpendicular para formar dos triángulos rectos. En cambio, podemos usar el hecho de que la relación de la medición de uno de los ángulos a la longitud de su lado opuesto será igual a las otras dos relaciones de medida de ángulo a lado opuesto. Veamos cómo se deriva esta afirmación al considerar el triángulo que se muestra en la Figura\(\PageIndex{5}\).
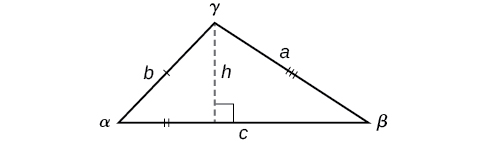
Figura\(\PageIndex{5}\)
Usando las relaciones del triángulo rectángulo, lo sabemos\(\sin \alpha=\dfrac{h}{b}\) y\(\sin \beta=\dfrac{h}{a}\). Resolver ambas ecuaciones para\(h\) da dos expresiones diferentes para\(h\).
\(h=b \sin \alpha\)y\(h=a \sin \beta\)
Luego establecemos las expresiones iguales entre sí.
\[\begin{align*} b \sin \alpha&= a \sin \beta\\ \left(\dfrac{1}{ab}\right)\left(b \sin \alpha\right)&= \left(a \sin \beta\right)\left(\dfrac{1}{ab}\right)\qquad \text{Multiply both sides by } \dfrac{1}{ab}\\ \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b} \end{align*}\]
De igual manera, podemos comparar las otras proporciones.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \gamma}{c}\)y\(\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Colectivamente, estas relaciones se llaman la Ley de los Sines.
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\)
Tenga en cuenta la forma estándar de etiquetar triángulos: ángulo\(\alpha\) (alfa) es lado opuesto\(a\); ángulo\(\beta\) (beta) es lado opuesto\(b\); y ángulo\(\gamma\) (gamma) es lado opuesto\(c\). Ver Figura\(\PageIndex{6}\).
Mientras calcula ángulos y lados, asegúrese de llevar los valores exactos a la respuesta final. Generalmente, las respuestas finales se redondean al décimo más cercano, a menos que se especifique lo contrario.
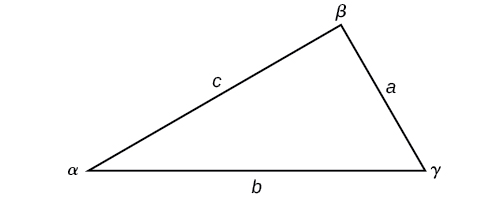
Figura\(\PageIndex{6}\)
Dado un triángulo con ángulos y lados opuestos etiquetados como en la Figura\(\PageIndex{6}\), la relación de la medición de un ángulo a la longitud de su lado opuesto será igual a las otras dos relaciones de medida de ángulo a lado opuesto. Todas las proporciones serán iguales. La Ley de los Sines se basa en proporciones y se presenta simbólicamente de dos maneras.
\[\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\]
\[\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\]
Para resolver un triángulo oblicuo, use cualquier par de proporciones aplicables.
Resuelve el triángulo que se muestra en la Figura\(\PageIndex{7}\) a la décima más cercana.
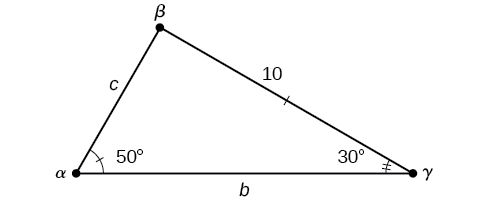
Figura\(\PageIndex{7}\)
Solución
Los tres ángulos deben sumar hasta 180 grados. A partir de esto, podemos determinar que
\[\begin{align*} \beta &= 180^{\circ} - 50^{\circ} - 30^{\circ}\\ &= 100^{\circ} \end{align*}\]
Para encontrar un lado desconocido, necesitamos conocer el ángulo correspondiente y una relación conocida. Conocemos ese ángulo\(\alpha=50°\) y su lado correspondiente\(a=10\). Podemos utilizar la siguiente proporción de la Ley de Sines para encontrar la longitud de\(c\).
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(30^{\circ})}{c}\\ c\dfrac{\sin(50^{\circ})}{10}&= \sin(30^{\circ})\qquad \text{Multiply both sides by } c\\ c&= \sin(30^{\circ})\dfrac{10}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate } c\\ c&\approx 6.5 \end{align*}\]
De igual manera, para resolver\(b\), establecemos otra proporción.
\[\begin{align*} \dfrac{\sin(50^{\circ})}{10}&= \dfrac{\sin(100^{\circ})}{b}\\ b \sin(50^{\circ})&= 10 \sin(100^{\circ})\qquad \text{Multiply both sides by } b\\ b&= \dfrac{10 \sin(100^{\circ})}{\sin(50^{\circ})}\qquad \text{Multiply by the reciprocal to isolate }b\\ b&\approx 12.9 \end{align*}\]
Por lo tanto, el conjunto completo de ángulos y lados es
\(\begin{matrix} \alpha=50^{\circ} & a=10\\ \beta=100^{\circ} & b\approx 12.9\\ \gamma=30^{\circ} & c\approx 6.5 \end{matrix}\)
Resuelve el triángulo que se muestra en la Figura\(\PageIndex{8}\) a la décima más cercana.
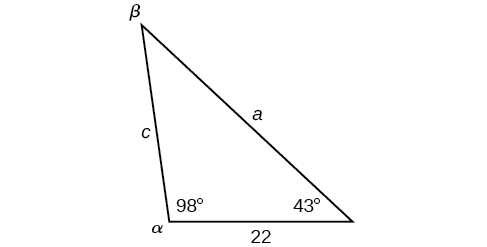
Figura\(\PageIndex{8}\)
- Contestar
-
\(\begin{matrix} \alpha=98^{\circ} & a=34.6\\ \beta=39^{\circ} & b=22\\ \gamma=43^{\circ} & c=23.8 \end{matrix}\)
Usando la ley de los senos para resolver triángulos de la SSA
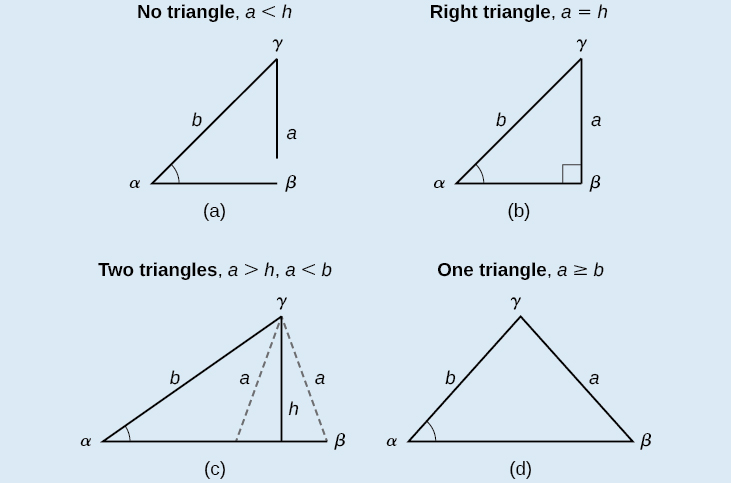
Podemos usar la Ley de los Sinos para resolver cualquier triángulo oblicuo, pero algunas soluciones pueden no ser sencillas. En algunos casos, más de un triángulo puede satisfacer los criterios dados, los cuales describimos como un caso ambiguo. Los triángulos clasificados como SSA, aquellos en los que conocemos las longitudes de dos lados y la medición del ángulo opuesto a uno de los lados dados, pueden resultar en una o dos soluciones, o incluso ninguna solución.
Los triángulos oblicuos en la categoría SSA pueden tener cuatro resultados diferentes. La figura\(\PageIndex{9}\) ilustra las soluciones con los lados conocidos\(a\)\(b\) y el ángulo conocido\(\alpha\).
Figura\(\PageIndex{9}\)
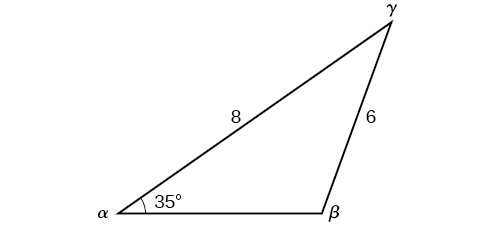
Resuelve el triángulo en la Figura\(\PageIndex{10}\) para el lado faltante y encuentra las medidas de ángulo faltantes a la décima más cercana.
Figura\(\PageIndex{10}\)
Solución
Usa la Ley de Sines para encontrar ángulo\(\beta\) y ángulo\(\gamma\), y luego lado\(c\). Resolviendo para\(\beta\), tenemos la proporción
\[\begin{align*} \dfrac{\sin \alpha}{a}&= \dfrac{\sin \beta}{b}\\ \dfrac{\sin(35^{\circ})}{6}&= \dfrac{\sin \beta}{8}\\ \dfrac{8 \sin(35^{\circ})}{6}&= \sin \beta\\ 0.7648&\approx \sin \beta\\ {\sin}^{-1}(0.7648)&\approx 49.9^{\circ}\\ \beta&\approx 49.9^{\circ} \end{align*}\]
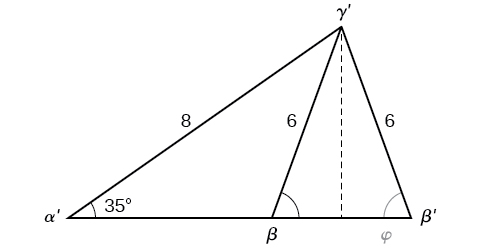
Sin embargo, en el diagrama, el ángulo\(\beta\) parece ser un ángulo obtuso y puede ser mayor que\(90°\). ¿Cómo conseguimos un ángulo agudo, y cómo encontramos la medición de\(\beta\)? Investiguemos más a fondo. Soltando una perpendicular desde\(\gamma\) y viendo el triángulo desde una perspectiva de ángulo recto, tenemos Figura\(\PageIndex{11}\). Parece que puede haber un segundo triángulo que se ajuste a los criterios dados.
Figura\(\PageIndex{11}\)
El ángulo suplementario a\(\beta\) es aproximadamente igual a\(49.9°\), lo que significa que\(\beta=180°−49.9°=130.1°\). (Recuerda que la función sinusoidal es positiva tanto en el primer como en el segundo cuadrantes.) Resolviendo para\(\gamma\), tenemos
\[\begin{align*} \gamma&= 180^{\circ}-35^{\circ}-130.1^{\circ}\\ &\approx 14.9^{\circ} \end{align*}\]
Entonces podemos usar estas medidas para resolver el otro triángulo. Ya que\(\beta′\) es complementario a\(\beta\), tenemos
\[\begin{align*} \gamma^{'}&= 180^{\circ}-35^{\circ}-49.5^{\circ}\\ &\approx 95.1^{\circ} \end{align*}\]
Ahora tenemos que encontrar\(c\) y\(c′\).
Tenemos
\[\begin{align*} \dfrac{c}{\sin(14.9^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c&= \dfrac{6 \sin(14.9^{\circ})}{\sin(35^{\circ})}\\ &\approx 2.7 \end{align*}\]
Por último,
\[\begin{align*} \dfrac{c'}{\sin(95.1^{\circ})}&= \dfrac{6}{\sin(35^{\circ})}\\ c'&= \dfrac{6 \sin(95.1^{\circ})}{\sin(35^{\circ})}\\ &\approx 10.4 \end{align*}\]
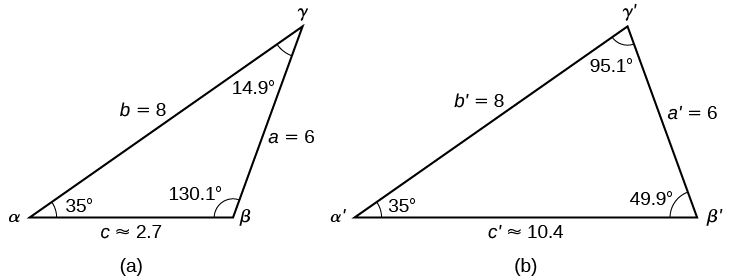
Para resumir, hay dos triángulos con un ángulo de\(35°\), un lado adyacente de 8, y un lado opuesto de 6, como se muestra en la Figura\(\PageIndex{12}\).
Figura\(\PageIndex{12}\)
No obstante, estábamos buscando los valores para el triángulo con un ángulo obtuso\(\beta\). Podemos verlas en el primer triángulo (a) en la Figura\(\PageIndex{12}\).
Dado\(\alpha=80°\),\(a=120\), y\(b=121\), encontrar el lado y los ángulos faltantes. Si hay más de una solución posible, mostrar ambas.
- Contestar
-
Solución 1
\(\begin{matrix} \alpha=80^{\circ} & a=120\\ \beta\approx 83.2^{\circ} & b=121\\ \gamma\approx 16.8^{\circ} & c\approx 35.2 \end{matrix}\)
Solución 2
\(\begin{matrix} \alpha '=80^{\circ} & a'=120\\ \beta '\approx 96.8^{\circ} & b'=121\\ \gamma '\approx 3.2^{\circ} & c'\approx 6.8 \end{matrix}\)
En el triángulo que se muestra en la Figura\(\PageIndex{13}\), resuelva para el lado y ángulos desconocidos. Redondea tus respuestas a la décima más cercana.
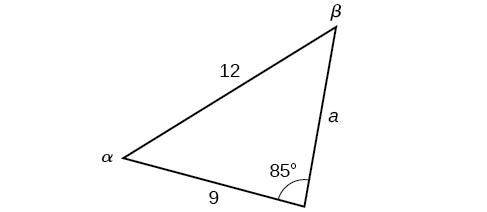
Figura\(\PageIndex{13}\)
Solución
Al elegir el par de ratios de la Ley de Sinos a utilizar, mira la información que se da. En este caso, conocemos el ángulo,\(\gamma=85°\), y su lado correspondiente\(c=12\), y sabemos lado\(b=9\). Usaremos esta proporción para resolver por\(\beta\).
\[\begin{align*} \dfrac{\sin(85^{\circ})}{12}&= \dfrac{\sin \beta}{9}\qquad \text{Isolate the unknown.}\\ \dfrac{9 \sin(85^{\circ})}{12}&= \sin \beta \end{align*}\]
Para buscar\(\beta\), aplique la función sinusoidal inversa. El seno inverso producirá un solo resultado, pero tenga en cuenta que puede haber dos valores para\(\beta\). Es importante verificar el resultado, ya que puede haber dos soluciones viables, una sola solución (el caso habitual), o ninguna solución.
\[\begin{align*} \beta&= {\sin}^{-1}\left(\dfrac{9 \sin(85^{\circ})}{12}\right)\\ \beta&\approx {\sin}^{-1} (0.7471)\\ \beta&\approx 48.3^{\circ} \end{align*}\]
En este caso, si restamos\(\beta\) de\(180°\), encontramos que puede haber una segunda solución posible. Así,\(\beta=180°−48.3°≈131.7°\). Para verificar la solución, restar ambos ángulos,\(131.7°\) y\(85°\), de\(180°\). Esto da
\[\begin{align*} \alpha&= 180^{\circ}-85^{\circ}-131.7^{\circ}\\ &\approx -36.7^{\circ} \end{align*}\]
lo cual es imposible, y así\(\beta≈48.3°\).
Para encontrar los valores faltantes restantes, calculamos\(\alpha=180°−85°−48.3°≈46.7°\). Ahora, solo\(a\) se necesita un lado. Utilizar la Ley de los Sinos para resolver\(a\) por una de las proporciones.
\[\begin{align*} \dfrac{\sin(85°)}{12}&= \dfrac{\sin(46.7^{\circ})}{a}\\ a\dfrac{\sin(85^{\circ})}{12}&= \sin(46.7^{\circ})\\ a&=\dfrac{12\sin(46.7^{\circ})}{\sin(85^{\circ})}\\ &\approx 8.8 \end{align*}\]
El conjunto completo de soluciones para el triángulo dado es
\(\begin{matrix} \alpha\approx 46.7^{\circ} & a\approx 8.8\\ \beta\approx 48.3^{\circ} & b=9\\ \gamma=85^{\circ} & c=12 \end{matrix}\)
Dado\(\alpha=80°\),\(a=100\),\(b=10\), encontrar el lado y los ángulos faltantes. Si hay más de una solución posible, mostrar ambas. Redondea tus respuestas a la décima más cercana.
- Contestar
-
\(\beta≈5.7°\),\(\gamma≈94.3°\),\(c≈101.3\)
Encuentra todos los triángulos posibles si un lado tiene longitud\(4\) opuesta a un ángulo de\(50°\), y un segundo lado tiene longitud\(10\).
Solución
Usando la información dada, podemos resolver para el ángulo opuesto al lado de la longitud\(10\). Ver Figura\(\PageIndex{14}\).
\[\begin{align*} \dfrac{\sin \alpha}{10}&= \dfrac{\sin(50^{\circ})}{4}\\ \sin \alpha&= \dfrac{10 \sin(50^{\circ})}{4}\\ \sin \alpha&\approx 1.915 \end{align*}\]
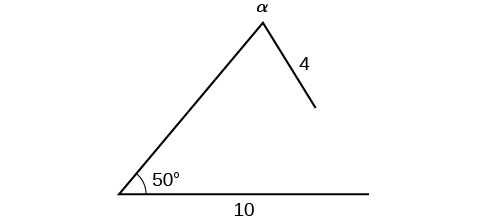
Figura\(\PageIndex{14}\)
Podemos parar aquí sin encontrar el valor de\(\alpha\). Debido a que el rango de la función sinusoidal es\([ −1,1 ]\), es imposible que el valor sinusoidal sea\(1.915\). De hecho, ingresar\({\sin}^{−1}(1.915)\) en una calculadora gráfica genera un DOMINIO DE ERROR. Por lo tanto, no se pueden dibujar triángulos con las dimensiones proporcionadas.
Determinar el número de triángulos posibles dado\(a=31\),\(b=26\),\(\beta=48°\).
- Contestar
-
dos
Encontrar el área de un triángulo oblicuo usando la función sinusoidal
Ahora que podemos resolver un triángulo para valores faltantes, podemos usar algunos de esos valores y la función seno para encontrar el área de un triángulo oblicuo. Recordemos que la fórmula de área para un triángulo se da como\(Area=\dfrac{1}{2}bh\), donde\(b\) es base y\(h\) es altura. Para los triángulos oblicuos, debemos encontrar\(h\) antes de poder usar la fórmula de área. Observando los dos triángulos en la Figura\(\PageIndex{15}\), uno agudo y otro obtuso, podemos dejar caer una perpendicular para representar la altura y luego aplicar la propiedad trigonométrica\(\sin \alpha=\dfrac{opposite}{hypotenuse}\) para escribir una ecuación para área en triángulos oblicuos. En el triángulo agudo, tenemos\(\sin \alpha=\dfrac{h}{c}\) o\(c \sin \alpha=h\). Sin embargo, en el triángulo obtuso, dejamos caer la perpendicular fuera del triángulo y extendemos la base\(b\) para formar un triángulo rectángulo. El ángulo utilizado en el cálculo es\(\alpha′\), o\(180−\alpha\).
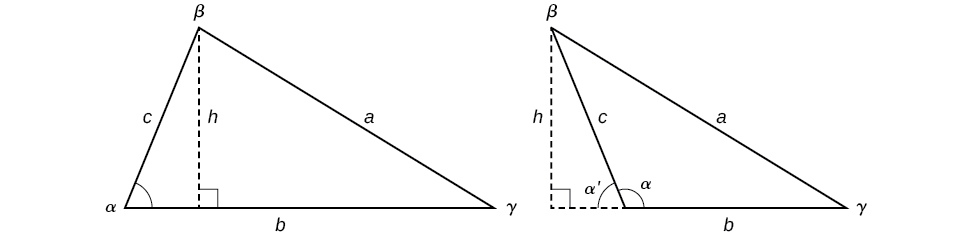
Figura\(\PageIndex{15}\)
Por lo tanto,
\(Area=\dfrac{1}{2}(base)(height)=\dfrac{1}{2}b(c \sin \alpha)\)
Del mismo modo,
\(Area=\dfrac{1}{2}a(b \sin \gamma)=\dfrac{1}{2}a(c \sin \beta)\)
La fórmula para el área de un triángulo oblicuo viene dada por
\[Area=\dfrac{1}{2}bc \sin \alpha\]
\[Area=\dfrac{1}{2}ac \sin \beta\]
\[Area=\dfrac{1}{2}ab \sin \gamma\]
Esto equivale a la mitad del producto de dos lados y el seno de su ángulo incluido.
Encuentra el área de un triángulo con lados\(a=90\),\(b=52\), y ángulo\(\gamma=102°\). Redondea el área al entero más cercano.
Solución
Usando la fórmula, tenemos
\[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\]
Encuentra el área del triángulo dado\(\beta=42°\),\(a=7.2 ft\),\(c=3.4 ft\). Redondea el área a la décima más cercana.
- Contestar
-
aproximadamente pies\(8.2\) cuadrados
Resolviendo Problemas Aplicados Usando la Ley de Sines
Cuanto más estudiamos las aplicaciones trigonométricas, más descubrimos que las aplicaciones son innumerables. Algunas son situaciones planas, de tipo diagrama, pero muchas aplicaciones en cálculo, ingeniería y física involucran tres dimensiones y movimiento.
Encuentra la altitud de la aeronave en el problema introducido al inicio de esta sección, que se muestra en la Figura\(\PageIndex{16}\). Redondea la altitud hasta la décima de milla más cercana.
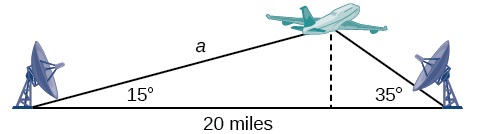
Figura\(\PageIndex{16}\)
Solución
Para encontrar la elevación de la aeronave, primero encontramos la distancia de una estación a la aeronave, como el lateral\(a\), y luego usamos relaciones de triángulo rectángulo para encontrar la altura de la aeronave,\(h\).
Debido a que los ángulos en el triángulo suman\(180\) grados, el ángulo desconocido debe ser\(180°−15°−35°=130°\). Este ángulo es opuesto al lado de la longitud\(20\), lo que nos permite establecer una relación de Ley de Sines.
\[\begin{align*} \dfrac{\sin(130^{\circ})}{20}&= \dfrac{\sin(35^{\circ})}{a}\\ a \sin(130^{\circ})&= 20 \sin(35^{\circ})\\ a&= \dfrac{20 \sin(35^{\circ})}{\sin(130^{\circ})}\\ a&\approx 14.98 \end{align*}\]
La distancia de una estación a la aeronave es de aproximadamente\(14.98\) millas.
Ahora que sabemos\(a\), podemos usar relaciones de triángulo rectángulo para resolver\(h\).
\[\begin{align*} \sin(15^{\circ})&= \dfrac{opposite}{hypotenuse}\\ \sin(15^{\circ})&= \dfrac{h}{a}\\ \sin(15^{\circ})&= \dfrac{h}{14.98}\\ h&= 14.98 \sin(15^{\circ})\\ h&\approx 3.88 \end{align*}\]
El avión se encuentra a una altitud de aproximadamente\(3.9\) millas.
El diagrama que se muestra en la Figura\(\PageIndex{17}\) representa la altura de un dirigible volando sobre un estadio de fútbol americano. Encuentra la altura del dirigible si el ángulo de elevación en la zona final sur, punto A, es\(70°\), el ángulo de elevación desde la zona final norte, punto B, es\(62°\), y la distancia entre los puntos de visión de las dos zonas finales es\(145\) yardas.
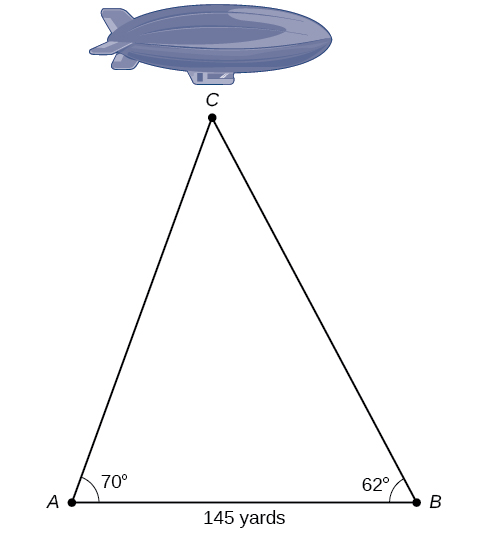
Figura\(\PageIndex{17}\)
- Contestar
-
\(161.9\)yd.
Medios
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con aplicaciones trigonométricas.
Ecuaciones Clave
| Ley de Sines |
\(\dfrac{\sin \alpha}{a}=\dfrac{\sin \beta}{b}=\dfrac{\sin \gamma}{c}\) \(\dfrac{a}{\sin \alpha}=\dfrac{b}{\sin \beta}=\dfrac{c}{\sin \gamma}\) |
| Área para triángulos oblicuos |
\(Area=\dfrac{1}{2}bc \sin \alpha\) \(=\dfrac{1}{2} ac \sin \beta\) \(=\dfrac{1}{2} ab \sin \gamma\) |
Conceptos clave
- La Ley de los Sinos puede ser utilizada para resolver triángulos oblicuos, que son triángulos no rectos.
- De acuerdo con la Ley de Sines, la relación de la medición de uno de los ángulos a la longitud de su lado opuesto equivale a las otras dos relaciones de medida de ángulo a lado opuesto.
- Hay tres casos posibles: ASA, AAS, SSA. Dependiendo de la información dada, podemos elegir la ecuación adecuada para encontrar la solución solicitada. Ver Ejemplo\(\PageIndex{1}\).
- El caso ambiguo surge cuando un triángulo oblicuo puede tener diferentes resultados.
- Hay tres casos posibles que surgen del arreglo de SSA: una sola solución, dos soluciones posibles y ninguna solución. Ver Ejemplo\(\PageIndex{2}\) y Ejemplo\(\PageIndex{3}\).
- La Ley de Sines puede ser utilizada para resolver triángulos con criterios dados. Ver Ejemplo\(\PageIndex{4}\).
- La fórmula general de área para triángulos se traduce en triángulos oblicuos al encontrar primero el valor de altura apropiado. Ver Ejemplo\(\PageIndex{5}\).
- Hay muchas aplicaciones trigonométricas. A menudo se pueden resolver dibujando primero un diagrama de la información dada y luego usando la ecuación apropiada. Ver Ejemplo\(\PageIndex{6}\).