8.3: Coordenadas polares

Objetivos de aprendizaje

• Trazar puntos usando coordenadas polares.
• Convertir de coordenadas polares a coordenadas rectangulares.
• Convertir de coordenadas rectangulares a coordenadas polares.
• Transformar ecuaciones entre formas polares y rectangulares.
• Identificar y graficar ecuaciones polares mediante la conversión a ecuaciones rectangulares.

A lo largo de\(12\) kilómetros del puerto, un velero encuentra mal tiempo y es arrastrado por un viento de\(16\) nudo (ver Figura\(\PageIndex{1}\)). ¿Cómo puede el marinero indicar su ubicación a la Guardia Costera? En esta sección, investigaremos un método de representación de la ubicación que es diferente de una cuadrícula de coordenadas estándar.

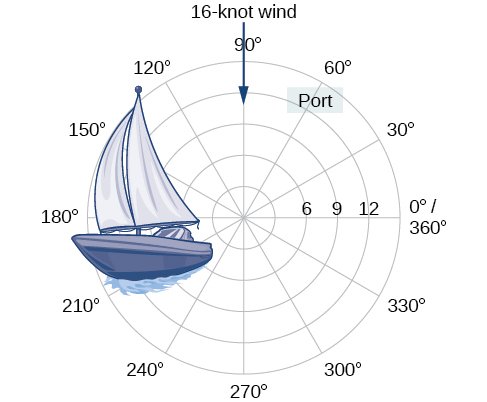
Figura\(\PageIndex{1}\)

Trazado de puntos mediante coordenadas polares

Cuando pensamos en trazar puntos en el plano, solemos pensar\((x,y)\) en coordenadas rectangulares en el plano de coordenadas cartesianas. Sin embargo, hay otras formas de escribir un par de coordenadas y otros tipos de sistemas de cuadrícula. En esta sección, introducimos las coordenadas polares, que son puntos etiquetados\((r,\theta)\) y trazados en una cuadrícula polar. La cuadrícula polar se representa como una serie de círculos concéntricos que irradian desde el polo, o el origen del plano de coordenadas.

La cuadrícula polar se escala como el círculo unitario con el eje positivo\(x\) ahora visto como el eje polar y el origen como polo. La primera coordenada\(r\) es el radio o longitud del segmento de línea dirigido desde el polo. El ángulo\(\theta\), medido en radianes, indica la dirección de\(r\). Nos movemos en sentido antihorario desde el eje polar por un ángulo de\(\theta\), y medimos un segmento de línea dirigida la longitud de\(r\) en la dirección de\(\theta\). Aunque medimos\(\theta\) primero y luego\(r\), el punto polar se escribe primero con la\(r\) coordenada -. Por ejemplo, para trazar el punto\(\left(2,\dfrac{\pi}{4}\right)\), moveríamos\(\dfrac{\pi}{4}\) unidades en sentido contrario a las agujas del reloj y luego una longitud de\(2\) desde el poste. Este punto se traza en la cuadrícula de la Figura\(\PageIndex{2}\).

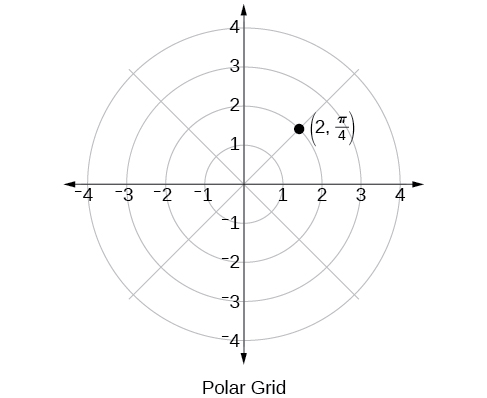
Figura\(\PageIndex{2}\)

Ejemplo\(\PageIndex{1}\): Plotting a Point on the Polar Grid

Trazar el punto\(\left(3,\dfrac{\pi}{2}\right)\) en la rejilla polar.

Solución

El ángulo\(\dfrac{\pi}{2}\) se encuentra barriendo en sentido contrario a las agujas del reloj\(90°\) desde el eje polar. El punto se ubica a una longitud de\(3\) unidades desde el poste en la\(\dfrac{\pi}{2}\) dirección, como se muestra en la Figura\(\PageIndex{3}\).

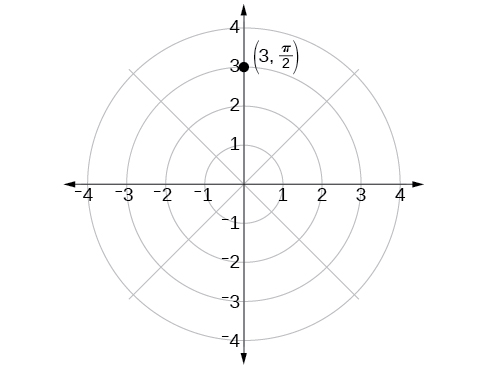
Figura\(\PageIndex{3}\)

Ejercicio\(\PageIndex{1}\)

Trazar el punto\(\left(2, \dfrac{\pi}{3}\right)\) en la rejilla polar.

Responder

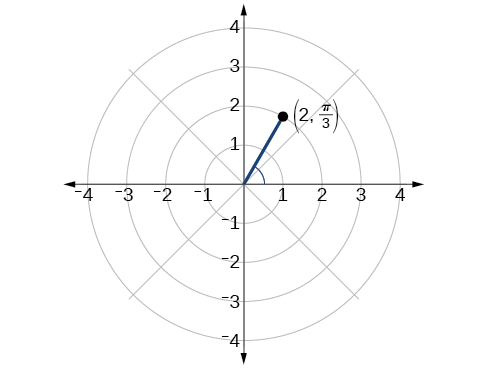
Figura\(\PageIndex{4}\)

Ejemplo\(\PageIndex{2}\): Plotting a Point in the Polar Coordinate System with a Negative Component

Trazar el punto\(\left(−2, \dfrac{\pi}{6}\right)\) en la rejilla polar.

Solución

Sabemos que\(\dfrac{\pi}{6}\) se encuentra en el primer cuadrante. Sin embargo,\(r=−2\). Podemos acercarnos a trazar un punto con un negativo\(r\) de dos maneras:

1. Trazar el punto\(\left(2,\dfrac{\pi}{6}\right)\) moviéndose\(\dfrac{\pi}{6}\) en el sentido contrario a las agujas del reloj y extendiendo una\(2\) unidad de segmento de línea dirigida hacia el primer cuadrante. Luego, vuelva a trazar el segmento de línea dirigido a través del poste y continúe\(2\) las unidades hacia el tercer cuadrante;
2. Muévase\(\dfrac{\pi}{6}\) en sentido contrario a las agujas del reloj y dibuje el segmento de línea dirigido desde\(2\) las unidades polares en dirección negativa, hacia el tercer cuadrante.

Ver Figura\(\PageIndex{5a}\). Compárelo con la gráfica de la coordenada polar\((2,π6)\) mostrada en la Figura\(\PageIndex{5b}\).

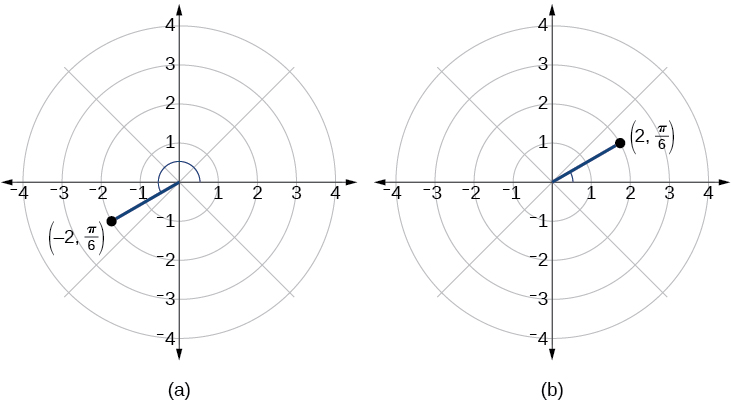
Figura\(\PageIndex{5}\)

Ejercicio\(\PageIndex{2}\)

Trazar los puntos\(\left(3,−\dfrac{\pi}{6}\right)\) y\(\left(2,\dfrac{9\pi}{4}\right)\) en la misma rejilla polar.

Responder

Figura\(\PageIndex{6}\)

Conversión de Coordenadas Polares a Coordenadas Rectangulares

Cuando se le da un conjunto de coordenadas polares, es posible que necesitemos convertirlas en coordenadas rectangulares. Para ello, podemos recordar las relaciones que existen entre las variables\(x\),\(y\),\(r\), y\(\theta\).

\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)

\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\)

Dejar caer una perpendicular desde el punto en el plano al eje x forma un triángulo rectángulo, como se ilustra en la Figura\(\PageIndex{7}\). Una manera fácil de recordar las ecuaciones anteriores es pensar en el lado adyacente sobre la hipotenusa y\(\sin \theta\) como el lado opuesto sobre la hipotenusa.\(\cos \theta\)

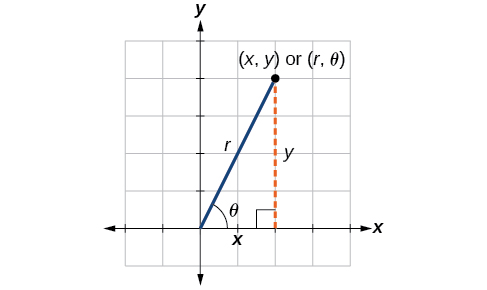
Figura\(\PageIndex{7}\)

Conversión de coordenadas polares a coordenadas rectangulares

Para convertir coordenadas polares\((r, \theta)\) en coordenadas rectangulares\((x, y)\), deje

\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]

\[\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\]

Cómo: Dadas las coordenadas polares, convertir a coordenadas rectangulares.

1. Dada la coordenada polar\((r,\theta)\), escribir\(x=r \cos \theta\) y\(y=r \sin \theta\).
2. Evaluar\(\cos \theta\) y\(\sin \theta\).
3. \(r\)Multiplique\(\cos \theta\) por para encontrar la coordenada\(x\) - de la forma rectangular.
4. \(r\)Multiplique\(\sin \theta\) por para encontrar la coordenada\(y\) - de la forma rectangular.

Ejemplo\(\PageIndex{3A}\): Writing Polar Coordinates as Rectangular Coordinates

Escribe las coordenadas polares\(\left(3,\dfrac{\pi}{2}\right)\) como coordenadas rectangulares.

Solución

Usa las relaciones equivalentes.

\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y&= 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]

Las coordenadas rectangulares son\((0,3)\). Ver Figura\(\PageIndex{8}\).

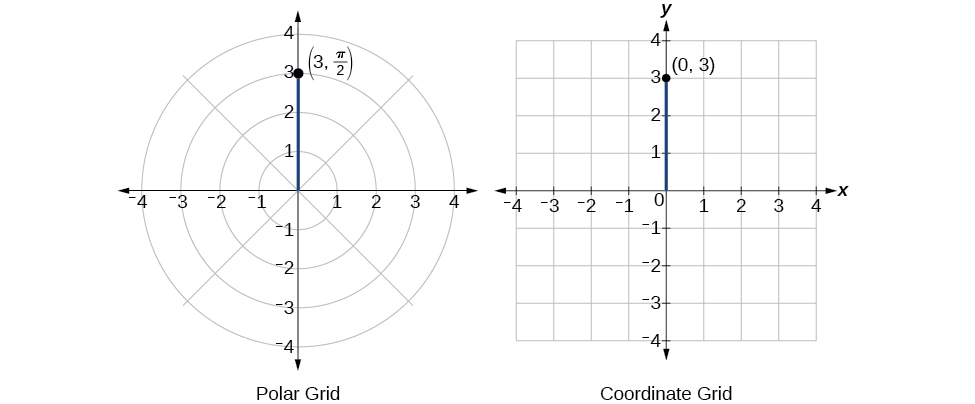
Figura\(\PageIndex{8}\)

Ejemplo\(\PageIndex{3B}\): Writing Polar Coordinates as Rectangular Coordinates

Escribe las coordenadas polares\((−2,0)\) como coordenadas rectangulares.

Solución

Ver Figura\(\PageIndex{9}\). Escribiendo las coordenadas polares como rectangulares, tenemos

\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]

Las coordenadas rectangulares también lo son\((−2,0)\).

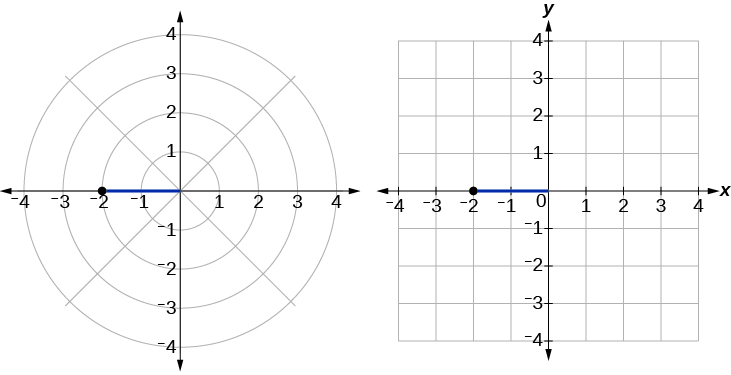
Figura\(\PageIndex{9}\)

Ejercicio\(\PageIndex{3}\)

Escribe las coordenadas polares\(\left(−1,\dfrac{2\pi}{3}\right)\) como coordenadas rectangulares.

Responder

\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)

Conversión de Coordenadas Rectangulares a Coordenadas Polares

Para convertir coordenadas rectangulares en coordenadas polares, usaremos otras dos relaciones familiares. Con esta conversión, sin embargo, necesitamos ser conscientes de que un conjunto de coordenadas rectangulares producirán más de un punto polar.

Conversión de coordenadas rectangulares a coordenadas polares

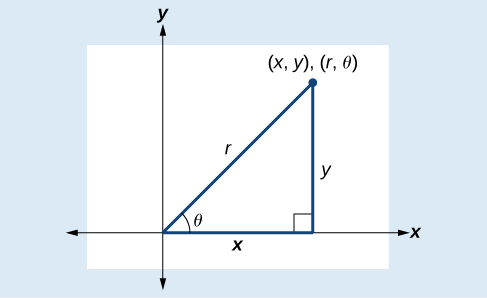
La conversión de coordenadas rectangulares a coordenadas polares requiere el uso de una o más de las relaciones ilustradas en la Figura\(\PageIndex{10}\).

\(\cos \theta=\dfrac{x}{r}\)o\(x=r \cos \theta\)

\(\sin \theta=\dfrac{y}{r}\)o\(y=r \sin \theta\)

\(r^2=x^2+y^2\)

\(\tan \theta=\dfrac{y}{x}\)

Figura\(\PageIndex{10}\)

Ejemplo\(\PageIndex{4}\): Writing Rectangular Coordinates as Polar Coordinates

Convierte las coordenadas rectangulares\((3,3)\) en coordenadas polares.

Solución

Vemos que el punto original\((3,3)\) está en el primer cuadrante. Para encontrar\(\theta\), usa la fórmula\(\tan \theta=\dfrac{y}{x}\). Esto da

\[\begin{align*} \tan \theta&= \dfrac{3}{3}\\ \tan \theta&= 1\\ {\tan}^{-1}(1)&= \dfrac{\pi}{4} \end{align*}\]

Para encontrar\(r\), sustituimos los valores por\(x\) y\(y\) en la fórmula\(r=\sqrt{x^2+y^2}\). Sabemos que\(r\) debe ser positivo, como\(\dfrac{\pi}{4}\) está en el primer cuadrante. Así

\[\begin{align*} r&= \sqrt{3^2+3^2}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]

Entonces,\(r=3\sqrt{2}\) y\(\theta=\dfrac{\pi}{4}\), dándonos el punto polar\((3\sqrt{2},\dfrac{\pi}{4})\). Ver Figura\(\PageIndex{11}\).

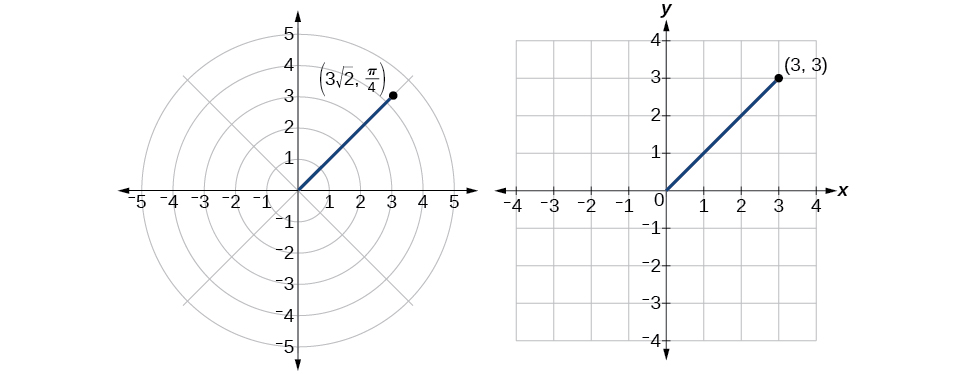
Figura\(\PageIndex{11}\)

Análisis

Hay otros conjuntos de coordenadas polares que serán las mismas que nuestra primera solución. Por ejemplo, los puntos\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) y\(\left(3\sqrt{2},−\dfrac{7\pi}{4}\right)\) coincidirán con la solución original de\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). El punto\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) indica un movimiento más en sentido antihorario por\(\pi\), que es directamente opuesto\(\dfrac{\pi}{4}\). El radio se expresa como\(−3\sqrt{2}\). Sin embargo, el ángulo\(\dfrac{5\pi}{4}\) se ubica en el tercer cuadrante y, como\(r\) es negativo, extendemos el segmento de línea dirigido en sentido contrario, hacia el primer cuadrante. Este es el mismo punto que\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). El punto\(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) es un movimiento más hacia la derecha por\(−\dfrac{7\pi}{4}\), desde\(\dfrac{\pi}{4}\). El radio,\(3\sqrt{2}\), es el mismo.

Transformación de ecuaciones entre formas polares y rectangulares

Ahora podemos convertir coordenadas entre forma polar y rectangular. Convertir ecuaciones puede ser más difícil, pero puede ser beneficioso poder convertir entre las dos formas. Dado que hay una serie de ecuaciones polares que no se pueden expresar claramente en forma cartesiana, y viceversa, podemos usar los mismos procedimientos que usamos para convertir puntos entre los sistemas de coordenadas. Entonces podemos usar una calculadora gráfica para graficar la forma rectangular o la forma polar de la ecuación.

Cómo: Dada una ecuación en forma polar, graficarla usando una calculadora gráfica

1. Cambia el MODO a POL, representando la forma polar.
2. Pulsa el botón Y= para abrir una pantalla que permita la entrada de seis ecuaciones:\(r_1\),\(r_2\),...,\(r_6\).
3. Ingresa la ecuación polar, establece igual a\(r\).
4. Presione GRAPH.

Ejemplo\(\PageIndex{5A}\): Writing a Cartesian Equation in Polar Form

Escribe la ecuación cartesiana\(x^2+y^2=9\) en forma polar.

Solución

El objetivo es eliminar\(x\) y\(y\) de la ecuación e introducir\(r\) y\(\theta\). Idealmente, escribiríamos la ecuación\(r\) en función de\(\theta\). Para obtener la forma polar, utilizaremos las relaciones entre\((x,y)\) y\((r,\theta)\). Desde\(x=r \cos \theta\) y\(y=r \sin \theta\), podemos sustituir y resolver por\(r\).

\(\begin{align*} {(r \cos \theta)}^2+{(r \sin \theta)}^2&= 9\\ r^2 {\cos}^2 \theta+r^2 {\sin}^2 \theta&= 9\\ r^2({\cos}^2 \theta+{\sin}^2 \theta)&= 9\\ r^2(1)&= 9\qquad \text {Substitute } {\cos}^2 \theta+{\sin}^2 \theta=1\\ r&= \pm 3\qquad \text {Use the square root property.} \end{align*}\)

Así,\(x^2+y^2=9\),\(r=3\), y\(r=−3\) debe generar la misma gráfica. Ver Figura\(\PageIndex{12}\).

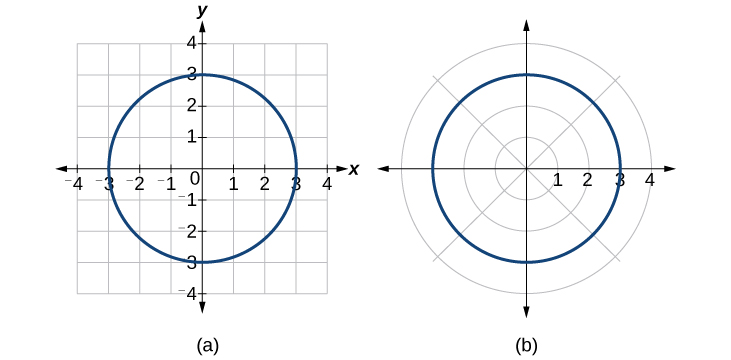
Figura\(\PageIndex{12}\): (a) Forma cartesiana\(x^2+y^2=9\) (b) Forma polar\(r=3\)

Para graficar un círculo en forma rectangular, primero debemos resolver para\(y\).

\[\begin{align*} x^2+y^2&= 9\\ y^2&= 9-x^2\\ y&= \pm \sqrt{9-x^2} \end{align*}\]

Tenga en cuenta que se trata de dos funciones separadas, ya que un círculo falla en la prueba de línea vertical. Por lo tanto, necesitamos ingresar las raíces cuadradas positivas y negativas en la calculadora por separado, como dos ecuaciones en la forma\(Y_1=\sqrt{9−x^2}\) y\(Y_2=−\sqrt{9−x^2}\). Presione GRAPH.

Ejemplo\(\PageIndex{5B}\): Rewriting a Cartesian Equation as a Polar Equation

Reescribir la ecuación cartesiana\(x^2+y^2=6y\) como una ecuación polar.

Solución

Esta ecuación parece similar al ejemplo anterior, pero requiere de diferentes pasos para convertir la ecuación.

Todavía podemos seguir los mismos procedimientos que ya aprendimos y hacer las siguientes sustituciones:

\(\begin{array}{ll} r^2=6y & \text{Use }x^2+y^2=r^2. \\ r^2=6r \sin \theta & \text{Substitute }y=r \sin \theta. \\ r^2−6r \sin \theta=0 & \text{Set equal to }0. \\ r(r−6 \sin \theta)=0 & \text{Factor and solve.} \\ r=0 & \text{We reject }r=0 \text{, as it only represents one point, }(0,0). \\ \text{or }r=6 \sin \theta \end{array}\)

Por lo tanto, las ecuaciones\(x^2+y^2=6y\) y\(r=6 \sin \theta\) deberían darnos la misma gráfica. Ver Figura\(\PageIndex{13}\).

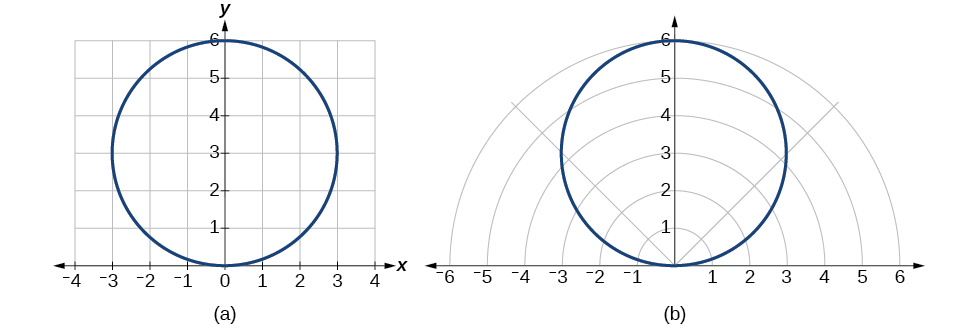
Figura\(\PageIndex{13}\): (a) Forma cartesiana\(x^2+y^2=6y\) (b) forma polar\(r=6 \sin \theta\)

La ecuación cartesiana o rectangular se traza en la cuadrícula rectangular, y la ecuación polar se traza en la cuadrícula polar. Claramente, las gráficas son idénticas.

Ejercicio\(\PageIndex{4A}\):

Reescribir una ecuación cartesiana en forma polar

Reescribir la ecuación cartesiana\(y=3x+2\) como una ecuación polar.

Responder

Vamos a utilizar las relaciones\(x=r \cos \theta\) y\(y=r \sin \theta\).

\(\begin{array}{cl} y=3x+2 \\ r \sin \theta=3r \cos \theta+2 \\ r \sin \theta−3r \cos \theta=2 \\ r(\sin \theta−3 \cos \theta)=2 & \text{Isolate }r. \\ r=2 \sin \theta−3\cos \theta & \text{Solve for }r. \end{array}\)

Ejercicio\(\PageIndex{4B}\):

Reescribir la ecuación cartesiana\(y^2=3−x^2\) en forma polar.

Responder

\(r=\sqrt{3}\)

Identificar y graficar ecuaciones polares mediante la conversión a ecuaciones rectangulares

Hemos aprendido a convertir coordenadas rectangulares en coordenadas polares, y hemos visto que los puntos son efectivamente los mismos. También hemos transformado ecuaciones polares en ecuaciones rectangulares y viceversa. Ahora demostraremos que sus gráficas, aunque dibujadas en diferentes cuadrículas, son idénticas.

Ejemplo\(\PageIndex{6A}\): Graphing a Polar Equation by Converting to a Rectangular Equation

Encubrir la ecuación polar\(r=2 \sec \theta\) a una ecuación rectangular, y dibujar su gráfica correspondiente.

Solución

La conversión es

\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \theta &=2 \\ x &=2 \end{align*}\]

Observe que la ecuación\(r=2 \sec \theta\) dibujada en la cuadrícula polar es claramente la misma que la línea vertical\(x=2\) dibujada en la cuadrícula rectangular (ver Figura\(\PageIndex{14}\)). Así como lo\(x=c\) es la forma estándar para una línea vertical en forma rectangular,\(r=c \sec \theta\) es la forma estándar para una línea vertical en forma polar.

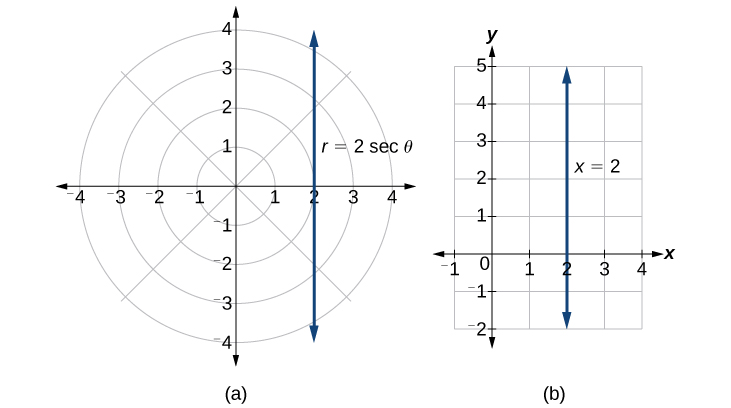
Figura\(\PageIndex{14}\): (a) Rejilla polar (b) Sistema de coordenadas rectangulares

Una discusión similar demostraría que la gráfica de la función\(r=2 \csc \theta\) será la línea horizontal\(y=2\). De hecho,\(r=c \csc \theta\) es la forma estándar para una línea horizontal en forma polar, correspondiente a la forma rectangular\(y=c\).

Ejemplo\(\PageIndex{6B}\): Rewriting a Polar Equation in Cartesian Form

Reescribir la ecuación polar\(r=\dfrac{3}{1−2 \cos \theta}\) como una ecuación cartesiana.

Solución

El objetivo es eliminar\(\theta\) y\(r\), e introducir\(x\) y\(y\). Despejamos la fracción, y luego usamos la sustitución. Para poder\(r\) sustituir por\(x\) y\(y\), debemos usar la expresión\(x^2+y^2=r^2\).

\(\begin{array} r =\dfrac{3}{1−2 \cos \theta} \\ r(1−2 \cos \theta)=3 \\ r\left(1−2\left(\dfrac{x}{r}\right)\right)=3 & \text{Use }\cos \theta=\dfrac{x}{r} \text{ to eliminate }\theta. \\ r−2x=3 \\ r=3+2x & \text{Isolate }r. \\ r^2={(3+2x)}^2 & \text{Square both sides.} \\ x^2+y^2={(3+2x)}^2 & \text{Use }x^2+y^2=r^2. \end{array}\)

La ecuación cartesiana es\(x^2+y^2={(3+2x)}^2\). Sin embargo, para graficarlo, especialmente usando una calculadora gráfica o un programa de computadora, queremos aislarlo\(y\).

\[\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\ y^2 &= {(3+2x)}^2-x^2 \\ y &= \pm {(3+2x)}^2-x^2 \end{align*}\]

Cuando toda nuestra ecuación ha sido cambiada desde\(r\) y\(\theta\) hacia\(x\) y\(y\), podemos detenernos, a menos que se le pida que resuelva\(y\) o simplifique. Ver Figura\(\PageIndex{15}\).

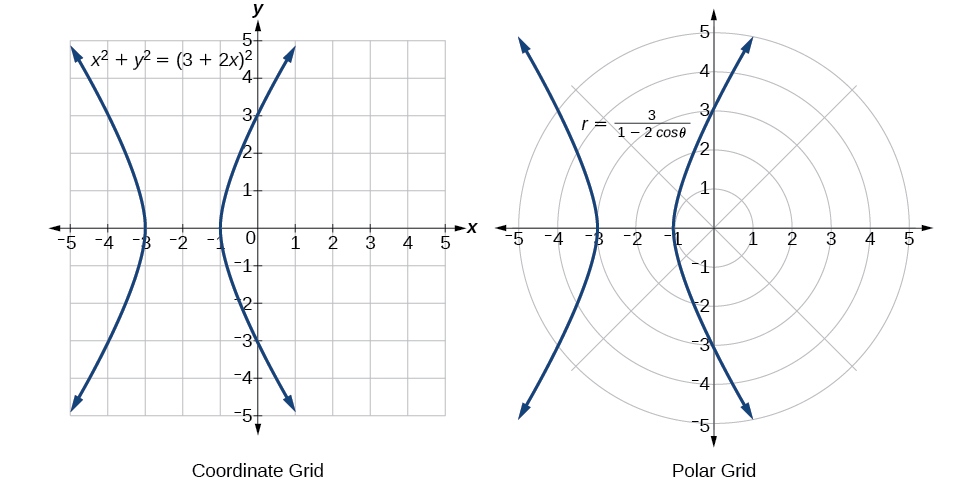
Figura\(\PageIndex{15}\)

La forma de “reloj de arena” de la gráfica se llama hipérbola. Las hipérbolas tienen muchas características y aplicaciones geométricas interesantes, que investigaremos más a fondo en Geometría Analítica.

Análisis

En este ejemplo, se puede ampliar el lado derecho de la ecuación y simplificar aún más la ecuación, como se muestra arriba. Sin embargo, la ecuación no puede escribirse como una sola función en forma cartesiana. Es posible que deseemos escribir la ecuación rectangular en la forma estándar de la hipérbola. Para ello, podemos comenzar con la ecuación inicial.

\(\begin{array}{ll} x^2+y^2={(3+2x)}^2 \\ x^2+y^2−{(3+2x)}^2=0 \\ x^2+y^2−(9+12x+4x^2)=0 \\ x^2+y^2−9−12x−4x^2=0 \\ −3x^2−12x+y^2=9 & \text{Multiply through by }−1. \\ 3x^2+12x−y^2=−9 \\ 3(x^2+4x)−y2=−9 & \text{Organize terms to complete the square for }x. \\ 3(x^2+4x+4)−y^2=−9+12 \\ 3{(x+2)}^2−y^2=3 \\ {(x+2)}^2−\dfrac{y^2}{3}=1\end{array}\)

Ejercicio\(\PageIndex{5}\)

Reescribir la ecuación polar\(r=2 \sin \theta\) en forma cartesiana.

Responder

\(x^2+y^2=2y\)o, en la forma estándar para un círculo,\(x^2+{(y−1)}^2=1\)

Ejemplo\(\PageIndex{7}\): Rewriting a Polar Equation in Cartesian Form

Reescribir la ecuación polar\(r=\sin(2\theta)\) en forma cartesiana.

Solución

\(\begin{array}{cl} r=\sin(2\theta) & \text{Use the double angle identity for sine.} \\ r=2 \sin \theta \cos \theta & \text{Use }\cos \theta=\dfrac{x}{r} \text{ and } \sin \theta=\dfrac{y}{r}. \\ r=2 \dfrac{x}{r})(\dfrac{y}{r}) & \text{ Simplify.} \\ r=\dfrac{2xy}{r^2} & \text{Multiply both sides by }r^2. \\ r^3=2xy \\ {(x^2+y^2)}^3=2xy & \text{As }x^2+y^2=r^2, r=\sqrt{x^2+y^2}. \end{array}\)

Esta ecuación también se puede escribir como

\({(x^2+y^2)}^{\frac{3}{2}}=2xy \text{ or }x^2+y^2={(2xy)}^{\frac{2}{3}}\)

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con coordenadas polares.

• Introducción a las coordenadas polares
• Comparación de coordenadas polares y rectangulares

Ecuaciones Clave

Fórmulas de conversión

\(\cos \theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\) \(\sin \theta=\dfrac{y}{r} \rightarrow y=r \sin \theta\) \(r^2=x^2+y^2\) \(\tan \theta=\dfrac{y}{x}\)

Conceptos clave

• La rejilla polar se representa como una serie de círculos concéntricos que irradian desde el polo u origen.
• Para trazar un punto en la forma\((r,\theta)\),\(\theta>0\), moverse en sentido contrario a las agujas del reloj desde el eje polar en un ángulo de\(\theta\), y luego extender un segmento de línea dirigida desde el polo la longitud de\(r\) en la dirección de\(\theta\). Si\(\theta\) es negativo, muévase en el sentido de las agujas del reloj y extienda un segmento de línea dirigido a la longitud de\(r\) en la dirección de\(\theta\). Ver Ejemplo\(\PageIndex{1}\).
• Si\(r\) es negativo, extienda el segmento de línea dirigido en la dirección opuesta a\(\theta\). Ver Ejemplo\(\PageIndex{2}\).
• Para convertir de coordenadas polares a coordenadas rectangulares, utilice las fórmulas\(x=r \cos \theta\) y\(y=r \sin \theta\). Ver Ejemplo\(\PageIndex{3}\) y Ejemplo\(\PageIndex{4}\).
• Para convertir de coordenadas rectangulares a coordenadas polares, utilice una o más de las fórmulas:\(\cos \theta=\dfrac{x}{r}\)\(\sin \theta=\dfrac{y}{r}\),\(\tan \theta=\dfrac{y}{x}\), y\(r=\sqrt{x^2+y^2}\). Ver Ejemplo\(\PageIndex{5}\).
• Transformar ecuaciones entre formas polares y rectangulares significa realizar las sustituciones apropiadas basadas en las fórmulas disponibles, junto con manipulaciones algebraicas. Ver Ejemplo\(\PageIndex{6}\)\(\PageIndex{7}\), Ejemplo y Ejemplo\(\PageIndex{8}\).
• El uso de las sustituciones adecuadas permite reescribir una ecuación polar como una ecuación rectangular, y luego graficarla en el plano rectangular. Ver Ejemplo\(\PageIndex{9}\)\(\PageIndex{10}\), Ejemplo y Ejemplo\(\PageIndex{11}\).