8.8: Vectores
- Page ID
- 121269
- Ver vectores geométricamente.
- Encuentra magnitud y dirección.
- Realizar adición de vectores y multiplicación escalar.
- Encuentra la forma componente de un vector.
- Encuentra el vector de unidad en la dirección de\(v\).
- Realizar operaciones con vectores en términos de\(i\) y\(j\).
- Encuentra el producto punto de dos vectores.
Un avión vuela a una velocidad aérea de\(200\) millas por hora con rumbo SE de\(140°\). Un viento del norte (de norte a sur) sopla a\(16.2\) millas por hora, como se muestra en la Figura\(\PageIndex{1}\). ¿Cuál es la velocidad de avance y el rodamiento real del avión?
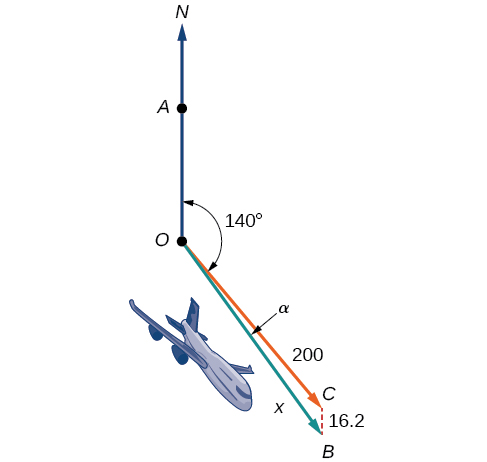
Figura\(\PageIndex{1}\)
La velocidad de avance se refiere a la velocidad de un avión con respecto al suelo. La velocidad aérea se refiere a la velocidad que un avión puede viajar en relación con su masa de aire circundante. Estas dos cantidades no son las mismas por el efecto del viento. En una sección anterior, utilizamos triángulos para resolver un problema similar que involucra el movimiento de embarcaciones. Posteriormente en esta sección, encontraremos la velocidad de avance y rumbo del avión, mientras investigamos otra aproximación a problemas de este tipo. Primero, sin embargo, examinemos los fundamentos de los vectores.
Una vista geométrica de vectores
Un vector es una cantidad específica dibujada como un segmento de línea con una punta de flecha en un extremo. Tiene un punto inicial, donde comienza, y un punto terminal, donde termina. Un vector se define por su magnitud, o la longitud de la línea, y su dirección, indicada por una punta de flecha en el punto terminal. Así, un vector es un segmento de línea dirigido. Hay varios símbolos que distinguen a los vectores de otras cantidades:
- Tipo minúsculas, negritas, con o sin una flecha en la parte superior como \(u\),\(w\),\(\overrightarrow{v}\),\(\overrightarrow{u}\),\(\overrightarrow{w}\).
- Dado el punto inicial\(P\) y el punto terminal\(Q\), un vector se puede representar como\(\overrightarrow{PQ}\). La punta de flecha en la parte superior es lo que indica que no es solo una línea, sino un segmento de línea dirigido.
- Dado un punto inicial de\((0,0)\) y un punto terminal\((a,b)\), un vector puede representarse como\(⟨a,b⟩\).
Este último símbolo\(⟨a,b⟩\) tiene un significado especial. Se llama la posición estándar. El vector de posición tiene un punto inicial\((0,0)\) y un punto terminal\(⟨a,b⟩\). Para cambiar cualquier vector al vector de posición, pensamos en el cambio en las coordenadas x y el cambio en las coordenadas y. Así, si el punto inicial de un vector\(\overrightarrow{CD}\) es\(C(x_1,y_1)\) y el punto terminal es\(D(x_2,y_2)\), entonces el vector de posición se encuentra calculando
\[\begin{align*} \overrightarrow{AB} &= ⟨x_2−x_1,y_2−y_1⟩ \\[4pt] &= ⟨a,b⟩ \end{align*}\]
En la Figura\(\PageIndex{2}\), vemos el vector original\(\overrightarrow{CD}\) y el vector de posición\(\overrightarrow{AB}\).
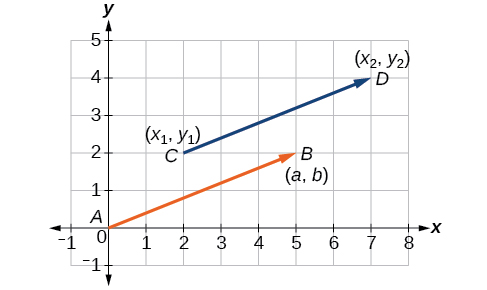
Figura\(\PageIndex{2}\)
Un vector es un segmento de línea dirigido con un punto inicial y un punto terminal. Los vectores se identifican por la magnitud, o la longitud de la línea, y la dirección, representados por la punta de flecha que apunta hacia el punto terminal. El vector de posición tiene un punto inicial en\((0,0)\) y es identificado por su punto terminal\(⟨a,b⟩\).
Considera el vector cuyo punto inicial es\(P(2,3)\) y el punto terminal es\(Q(6,4)\). Encuentra el vector de posición.
Solución
El vector de posición se encuentra restando una\(x\) coordenada de la otra\(x\) coordenada y una\(y\) coordenada de la otra\(y\) coordenada. Así
\[\begin{align*} v &= ⟨6−2,4−3⟩ \\[4pt] &=⟨4,1⟩ \end{align*}\]
El vector de posición comienza en\((0,0)\) y termina en\((4,1)\). Las gráficas de ambos vectores se muestran en la Figura\(\PageIndex{3}\).
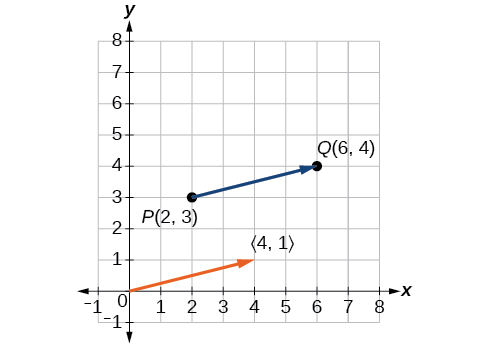
Figura\(\PageIndex{3}\)
Vemos que el vector de posición es\(⟨4,1⟩\).
Encuentra el vector de posición dado que el vector\(v\) tiene un punto inicial en\((−3,2)\) y un punto terminal en\((4,5)\), luego grafica ambos vectores en el mismo plano.
Solución
El vector de posición se encuentra utilizando el siguiente cálculo:
\[\begin{align*} v &= ⟨4−(−3),5−2⟩ \\[4pt] &= ⟨7,3⟩ \end{align*}\]
Así, el vector de posición comienza en\((0,0)\) y termina en\((7,3)\). Ver Figura\(\PageIndex{4}\).
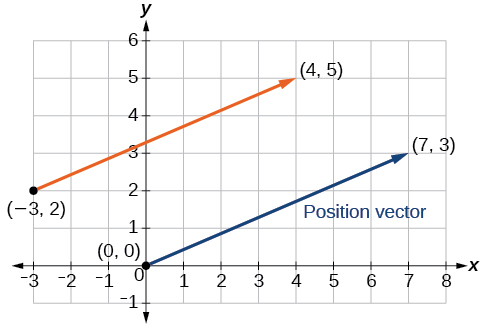
Figura\(\PageIndex{4}\)
Dibuja un vector\(\vec{v}\) que conecte desde el origen hasta el punto\((3,5)\).
- Contestar
-
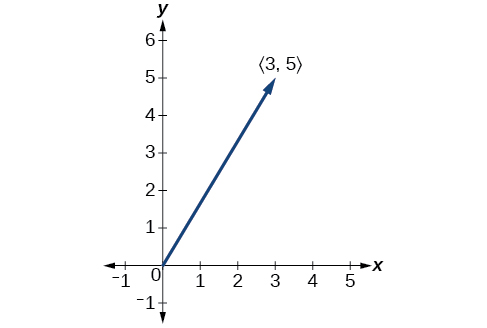
Figura\(\PageIndex{5}\)
Encontrar magnitud y dirección
Para trabajar con un vector, necesitamos poder encontrar su magnitud y su dirección. Encontramos su magnitud usando el Teorema de Pitágoras o la fórmula de distancia, y encontramos su dirección usando la función tangente inversa.
Dado un vector de posición\(\vec{v}=⟨a,b⟩\), la magnitud se encuentra por\(| v |=\sqrt{a^2+b^2}\) .La dirección es igual al ángulo formado con el\(x\) eje -o con el\(y\) eje -eje, dependiendo de la aplicación. Para un vector de posición, la dirección se encuentra por\(\tan \theta=\left(\dfrac{b}{a}\right)⇒\theta={\tan}^{−1}\left(\dfrac{b}{a}\right)\), como se ilustra en la Figura\(\PageIndex{6}\).
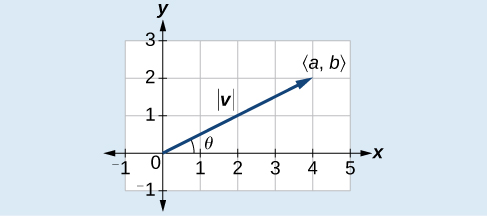
Figura\(\PageIndex{6}\)
Dos vectores\(\vec{v}\) y\(\vec{u}\) se consideran iguales si tienen la misma magnitud y la misma dirección. Adicionalmente, si ambos vectores tienen el mismo vector de posición, son iguales.
Encuentra la magnitud y dirección del vector con punto inicial\(P(−8,1)\) y punto\(Q(−2,−5)\) terminal.Dibuja el vector.
Solución
Primero, encuentra el vector de posición.
\[\begin{align*} u &= ⟨−2,−(−8),−5−1⟩ \\[4pt] &= ⟨6,−6⟩ \end{align*}\]
Utilizamos el Teorema de Pitágoras para encontrar la magnitud.
\[\begin{align*} |u| &= \sqrt{{(6)}^2+{(−6)}^2} \\[4pt] &= \sqrt{72} \\[4pt] &=\sqrt{62} \end{align*}\]
La dirección se da como
\[\begin{align*} \tan \theta & =\dfrac{−6}{6}=−1\rightarrow \theta={\tan}^{−1}(−1) \\[4pt] &= −45° \end{align*}\]
No obstante, el ángulo termina en el cuarto cuadrante, por lo que sumamos\(360°\) para obtener un ángulo positivo. Por lo tanto,\(−45°+360°=315°\). Ver Figura\(\PageIndex{7}\).
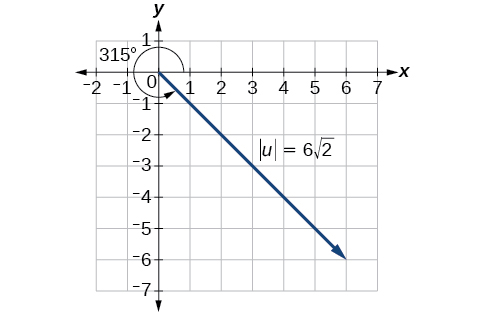
Figura\(\PageIndex{7}\)
Mostrar que el vector\(\vec{v}\) con punto inicial en\((5,−3)\) y punto terminal en\((−1,2)\) es igual al vector\(\vec{u}\) con punto inicial en\((−1,−3)\) y punto terminal en\((−7,2)\). Dibuja el vector de posición en la misma cuadrícula que\(\vec{v}\) y\(\vec{u}\). A continuación, encuentra la magnitud y dirección de cada vector.
Solución
Como se muestra en la Figura\(\PageIndex{8}\), dibuje el vector\(\vec{v}\) comenzando en el punto inicial\((5,−3)\) y terminal\((−1,2)\). Dibuja el vector\(\vec{u}\) con punto inicial\((−1,−3)\) y punto terminal\((−7,2)\). Encuentra la posición estándar para cada uno.
A continuación, busque y dibuje el vector de posición para\(\vec{v}\) y\(\vec{u}\). Tenemos
\[\begin{align*} v &= ⟨−1−5,2−(−3)⟩ \\[4pt] &= ⟨−6,5⟩u \\[4pt] &= ⟨−7−(−1),2−(−3)⟩ \\[4pt] & =⟨−6,5⟩ \end{align*}\]
Ya que los vectores de posición son los mismos,\(\vec{v}\) y\(\vec{u}\) son los mismos.
Una forma alternativa de verificar la igualdad de vectores es mostrar que la magnitud y la dirección son las mismas para ambos vectores. Para demostrar que las magnitudes son iguales, usa el Teorema de Pitágoras.
\[\begin{align*} |v| &= \sqrt{{(−1−5)}^2+{(2−(−3))}^2} \\[4pt] &= \sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \\[4pt] |u| &= \sqrt{{(−7−(−1))}^2+{(2−(−3))}^2} \\[4pt] &=\sqrt{{(−6)}^2+{(5)}^2} \\[4pt] &= \sqrt{36+25} \\[4pt] &= \sqrt{61} \end{align*}\]
Como las magnitudes son iguales, ahora necesitamos verificar la dirección. El uso de la función tangente con el vector de posición da
\[\begin{align*} \tan \theta &= −\dfrac{5}{6}⇒\theta={\tan}^{−1}\left(−\dfrac{5}{6}\right) \\[4pt] & = −39.8° \end{align*}\]
No obstante, podemos ver que el vector de posición termina en el segundo cuadrante, por lo que sumamos\(180°\). Así, la dirección es\(−39.8°+180°=140.2°\).
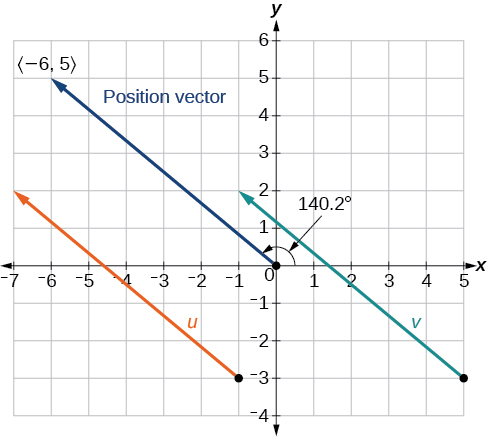
Figura\(\PageIndex{8}\)
Realización de Adición de Vectores y Multiplicación Escalar
Ahora que entendemos las propiedades de los vectores, podemos realizar operaciones que los involucren. Si bien es conveniente pensar en el vector\(u=⟨x,y⟩\) como una flecha o segmento de línea dirigida desde el origen hasta el punto\((x,y)\), los vectores pueden estar situados en cualquier parte del plano. La suma de dos vectores\(\vec{u}\) y\(\vec{v}\), o adición de vector, produce un tercer vector\(\overrightarrow{u+ v}\), el vector resultante.
Para encontrar\(\overrightarrow{u + v}\), primero dibujamos el vector\(\vec{u}\), y desde el extremo terminal de\(\vec{u}\), dibujamos el vector\(\vec{v}\). En otras palabras, tenemos el punto inicial de\(\vec{v}\) cumplir con el final terminal de\(\vec{u}\). Esta posición corresponde a la noción de que nos movemos a lo largo del primer vector y luego, desde su punto terminal, nos movemos a lo largo del segundo vector. La suma\(\overrightarrow{u + v}\) es el vector resultante porque resulta de la suma o resta de dos vectores. El vector resultante viaja directamente desde el principio\(\vec{u}\) hasta el final de\(\vec{v}\) en una trayectoria recta, como se muestra en la Figura\(\PageIndex{9}\).
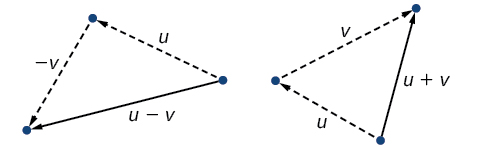
Figura\(\PageIndex{9}\)
La resta de vectores es similar a la suma de vectores. Para encontrar\(\overrightarrow{u − v}\), verlo como\(\overrightarrow{u + (−v)}\). Agregar\(\overrightarrow{−v}\) es invertir la dirección de\(\vec{v}\) y agregarlo al final de\(\vec{u}\). El nuevo vector comienza al inicio\(\vec{u}\) y se detiene en el punto final de\(\overrightarrow{−v}\). Consulte la Figura\(\PageIndex{10}\) para una imagen que compara la suma vectorial y la resta vectorial usando paralelogramos.
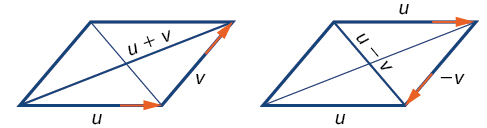
Figura\(\PageIndex{10}\)
Dado\(u=⟨3,−2⟩\) y\(v=⟨−1,4⟩\), encontrar dos nuevos vectores\(\overrightarrow{u + v}\), y\(\overrightarrow{u − v}\).
Solución
Para encontrar la suma de dos vectores, agregamos los componentes. Por lo tanto,
\[ \begin{align*} u+v &= ⟨3,−2⟩+⟨−1,4⟩ \\[4pt] &= ⟨3+(−1),−2+4⟩ \\[4pt] &=⟨2,2⟩ \end{align*}\]
Ver Figura\(\PageIndex{11a}\).
Para encontrar la diferencia de dos vectores, agregue los componentes negativos de\(\vec{v}\) a\(\vec{u}\). Por lo tanto,
\[\begin{align*}u+(−v) &=⟨3,−2⟩+⟨1,−4⟩ \\[4pt] &= ⟨3+1,−2+(−4)⟩ \\[4pt] &= ⟨4,−6⟩ \end{align*}\]
Ver Figura\(\PageIndex{11b}\).
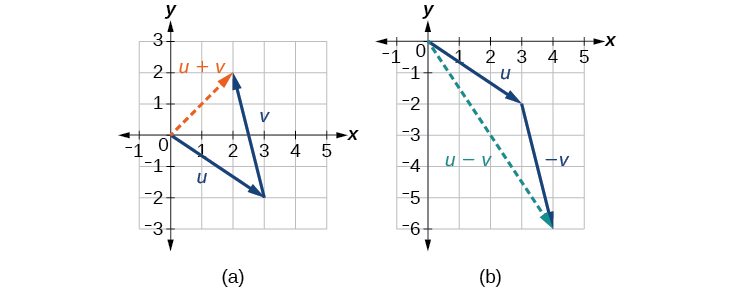
Figura\(\PageIndex{11}\): (a) Suma de dos vectores (b) Diferencia de dos vectores
Multiplicar por un escalar
Si bien sumar y restar vectores nos da un nuevo vector con una magnitud y dirección diferentes, el proceso de multiplicar un vector por un escalar, una constante, cambia solo la magnitud del vector o la longitud de la línea. La multiplicación escalar no tiene ningún efecto en la dirección a menos que el escalar sea negativo, en cuyo caso la dirección del vector resultante es opuesta a la dirección del vector original.
La multiplicación escalar implica el producto de un vector y un escalar. Cada componente del vector se multiplica por el escalar. Así, para multiplicar\(v=⟨a,b⟩\) por\(k\), tenemos
\(kv=⟨ka,kb⟩\)
Solo cambia la magnitud, a menos que\(k\) sea negativa, y luego el vector invierte la dirección.
Dado vector \(\vec{v}=⟨3,1⟩\), encontrar\(3\vec{v}\),\(\dfrac{1}{2}\), y\(\vec{−v}\).
Solución
Ver Figura\(\PageIndex{12}\) para una interpretación geométrica. Si\(\vec{v}=⟨3,1⟩\), entonces
\[\begin{align*} 3v &= ⟨3⋅3,3⋅1⟩ \\[4pt] &= ⟨9,3⟩ \\[4pt] \dfrac{1}{2}v &= ⟨\dfrac{1}{2}⋅3,\dfrac{1}{2}⋅1⟩ \\[4pt] &=⟨\dfrac{3}{2},\dfrac{1}{2}⟩ \\[4pt] −v &=⟨−3,−1⟩ \end{align*}\]
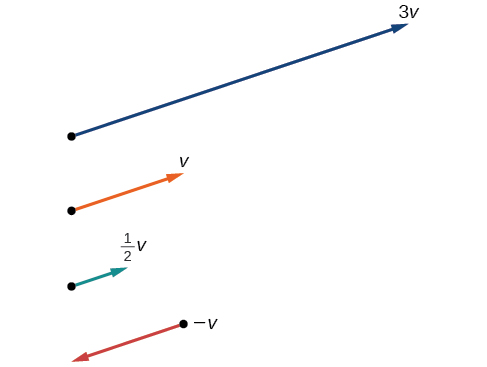
Figura\(\PageIndex{12}\)
Análisis
Observe que el vector\(3\vec{v}\) es tres veces la longitud de\(\vec{v}\),\(\dfrac{1}{2}\vec{v}\) es la mitad de la longitud de\(\vec{v}\), y\(\overrightarrow{–v}\) es la misma longitud de\(\vec{v}\), pero en la dirección opuesta.
Encuentra el múltiplo escalar\(3u\) dado\(\vec{u}=⟨5,4⟩\).
- Contestar
-
\(3u=⟨15,12⟩\)
Encuentra una ecuación lineal para resolver para las siguientes cantidades desconocidas: Un número excede a otro número por\(17\) y su suma es\(31\). Encuentra los dos números.
Solución
Primero, debemos multiplicar cada vector por el escalar.
\[\begin{align*} 3u &= 3⟨3,−2⟩ \\[4pt] &= ⟨9,−6⟩ \\[4pt] 2v &= 2⟨−1,4⟩ \\[4pt] &= ⟨−2,8⟩ \end{align*}\]
Después, sumar los dos juntos.
\[\begin{align*} w &= 3u+2v \\[4pt] &=⟨9,−6⟩+⟨−2,8⟩ \\[4pt] &= ⟨9−2,−6+8⟩ \\[4pt] &= ⟨7,2⟩ \end{align*}\]
Entonces,\(w=⟨7,2⟩\).
Búsqueda de formulario de componente
En algunas aplicaciones que involucran vectores, es útil para nosotros poder descomponer un vector en sus componentes. Los vectores están compuestos por dos componentes: el componente horizontal es la\(x\) dirección y el componente vertical es la\(y\) dirección. Por ejemplo, podemos ver en la gráfica de la Figura\(\PageIndex{13}\) que el vector de posición\(⟨2,3⟩\) proviene de sumar los vectores\(v_1\) y\(v_2\). Tenemos\(v_2\) con punto inicial\((0,0)\) y punto terminal\((2,0)\).
\[\begin{align*} v_1 &= ⟨2−0,0−0⟩ \\[4pt] &= ⟨2,0⟩ \end{align*}\]
También tenemos\(v_2\) con punto inicial\((0,0)\) y punto terminal\((0, 3)\).
\[\begin{align*} v_2 &= ⟨0−0,3−0⟩ \\[4pt] &= ⟨0,3⟩ \end{align*}\]
Por lo tanto, el vector de posición es
\[\begin{align*} v &= ⟨2+0,3+0⟩ \\[4pt] &= ⟨2,3⟩ \end{align*}\]
Usando el Teorema de Pitágoras, la magnitud de\(v_1\) es\(2\), y la magnitud de\(v_2\) es\(3\). Para encontrar la magnitud de\(v\), use la fórmula con el vector de posición.
\[\begin{align*} |v| &= \sqrt{{|v_1|}^2+{|v_2|}^2} \\[4pt] &= \sqrt{2^2+3^2} \\[4pt] &= \sqrt{13} \end{align*}\]
La magnitud de\(v\) es\(\sqrt{13}\). Para encontrar la dirección, utilizamos la función tangente\(\tan \theta=\dfrac{y}{x}\).
\[\begin{align*} \tan \theta &= \dfrac{v_2}{v_1} \\[4pt] \tan \theta &= \dfrac{3}{2} \\[4pt] \theta &={\tan}^{−1}\left(\dfrac{3}{2}\right)=56.3° \end{align*}\]
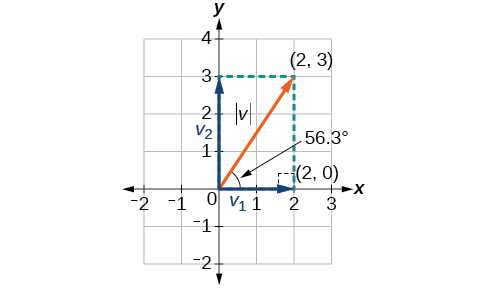
Figura\(\PageIndex{13}\)
Así, la magnitud de\(\vec{v}\) es\(\sqrt{13}\) y la dirección está\(56.3^{\circ}\) fuera de la horizontal.
Encuentra los componentes del vector \(\vec{v}\)con punto inicial\((3,2)\) y punto terminal\((7,4)\).
Solución
Primero encuentra la posición estándar.
\[\begin{align*} v &= ⟨7−3,4−2⟩ \\[4pt] &= ⟨4,2⟩ \end{align*}\]
Ver la ilustración en la Figura\(\PageIndex{14}\).
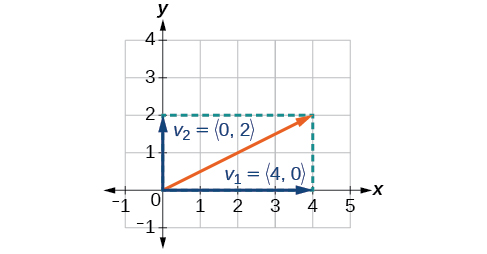
Figura\(\PageIndex{14}\)
El componente horizontal es\(\vec{v_1}=⟨4,0⟩\) y el componente vertical es\(\vec{v_2}=⟨0,2⟩\).
Encontrar el vector de unidad en la dirección de\(v\)
Además de encontrar los componentes de un vector, también es útil para resolver problemas encontrar un vector en la misma dirección que el vector dado, pero de magnitud\(1\). Llamamos a un vector con una magnitud de\(1\) un vector unitario. Entonces podemos preservar la dirección del vector original mientras simplificamos los cálculos.
Los vectores unitarios se definen en términos de componentes. El vector unitario horizontal se escribe como\(\vec{i}=⟨1,0⟩\) y se dirige a lo largo del eje horizontal positivo. El vector de unidad vertical se escribe como\(\vec{j}=⟨0,1⟩\) y se dirige a lo largo del eje vertical positivo. Ver Figura\(\PageIndex{15}\).
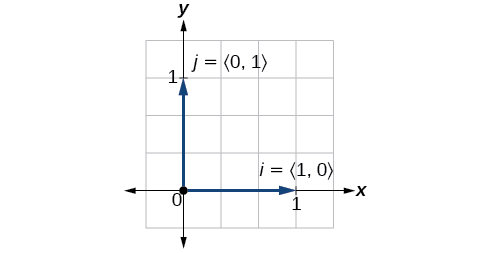
Figura\(\PageIndex{15}\)
Si \(\vec{v}\)es un vector distinto de cero, entonces\(\dfrac{v}{| v |}\) es un vector unitario en la dirección de \(v\). Cualquier vector dividido por su magnitud es un vector unitario. Observe que la magnitud es siempre un escalar, y dividir por un escalar es lo mismo que multiplicar por el recíproco del escalar.
Encuentra un vector de unidad en la misma dirección que\(v=⟨−5,12⟩\).
Solución
Primero, encontraremos la magnitud.
\[\begin{align*} |v| &= \sqrt{{(−5)}^2+{(12)}^2} \\[4pt] &= \sqrt{25+144} \\[4pt] &=\sqrt{169} \\[4pt] &= 13 \end{align*}\]
Luego dividimos cada componente por\(| v |\), lo que da un vector unitario en la misma dirección que\(\vec{v}\):
\(\dfrac{v}{| v |} = −\dfrac{5}{13}i+\dfrac{12}{13}j \)
o, en forma de componente
\(\dfrac{v}{| v |}= \left \langle -\dfrac{5}{13},\dfrac{12}{13} \right \rangle\)
Ver Figura\(\PageIndex{16}\).
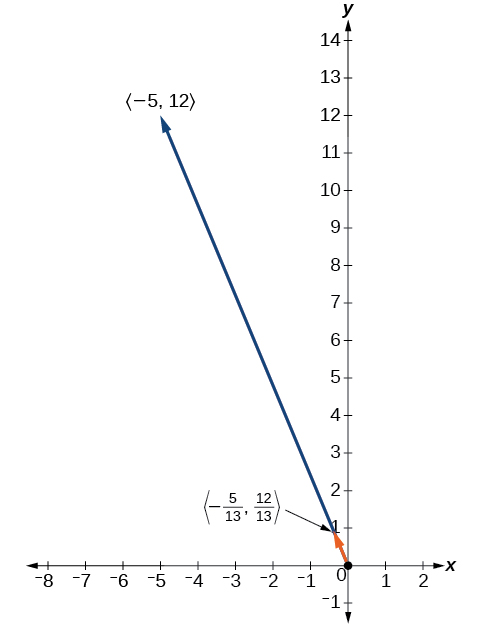
Figura\(\PageIndex{16}\)
Verificar que la magnitud del vector unitario sea igual\(1\). La magnitud de\(−\dfrac{5}{13}i+\dfrac{12}{13}j\) se da como
\[\begin{align*} \sqrt{ {\left(−\dfrac{5}{13}\right)}^2+{ \left(\dfrac{12}{13}\right) }^2 } &= \sqrt{\dfrac{25}{169}+\dfrac{144}{169}} \\[4pt] &= \sqrt{\dfrac{169}{169}}\\ &=1 \end{align*}\]
El vector\(u=\dfrac{5}{13}i+\dfrac{12}{13}j\) es el vector unitario en la misma dirección que\(v=⟨−5,12⟩\).
Realización de Operaciones con Vectores en términos de\(i\) y\(j\)
Hasta el momento, hemos investigado los fundamentos de los vectores: magnitud y dirección, suma y resta de vectores, multiplicación escalar, los componentes de los vectores y la representación de vectores geométricamente. Ahora que estamos familiarizados con las estrategias generales utilizadas para trabajar con vectores, representaremos vectores en coordenadas rectangulares en términos de\(i\) y\(j\).
Dado un vector\(\vec{v}\) con punto inicial\(P=(x_1,y_1)\) y punto terminal\(Q=(x_2,y_2)\),\(\vec{v}\) se escribe como
\[v=(x_2−x_1)i+(y_1−y_2)j\]
El vector de posición desde\((0,0)\) hasta\((a,b)\), donde\((x_2−x_1)=a\) y\((y_2−y_1)=b\), se escribe como\(\vec{v} = \vec{ai}+ \vec{bj}\). Esta suma vectorial se denomina una combinación lineal de los vectores\(\vec{i}\) y\(\vec{j}\).
La magnitud de\(\vec{v} = \overrightarrow{ai} + \overrightarrow{bj}\) se da como\(| v |=\sqrt{a^2+b^2}\). Ver Figura\(\PageIndex{17}\).
.jpg)
Figura\(\PageIndex{17}\)
Dado un vector\(\vec{v}\) con punto inicial\(P=(2,−6)\) y punto terminal\(Q=(−6,6)\), escriba el vector en términos de\(\vec{i}\) y\(\vec{j}\).
Solución
Comience por escribir la forma general del vector. Luego reemplace las coordenadas con los valores dados.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] &=(−6−2)i+(6−(−6))j \\[4pt] &= −8i+12j \end{align*}\]
Dado el punto inicial\(P_1=(−1,3)\) y el punto terminal\(P_2=(2,7)\), escriba el vector\(\vec{v}\) en términos de\(\vec{i}\) y\(\vec{j}\).
Solución
Comience por escribir la forma general del vector. Luego reemplace las coordenadas con los valores dados.
\[\begin{align*} v &= (x_2−x_1)i+(y_2−y_1)j \\[4pt] v &= (2−(−1))i+(7−3)j \\[4pt] &= 3i+4j \end{align*}\]
Escribe el vector\(\vec{u}\) con punto inicial\(P=(−1,6)\) y punto terminal\(Q=(7,−5)\) en términos de\(\vec{i}\) y\(\vec{j}\).
- Contestar
-
\(u=8i−11j\)
Realización de Operaciones en Vectores en términos de\(i\) y\(j\)
Cuando los vectores se escriben en términos de\(i\) y\(j\), podemos llevar a cabo suma, resta y multiplicación escalar realizando operaciones en los componentes correspondientes.
Dado\(v = ai + bj\) y\(u = ci + dj\), entonces
\[\begin{align*} v+u &= (a+c)i+(b+d)j \\[4pt] v−u &= (a−c)i+(b−d)j \end{align*}\]
Encuentra la suma de\(v_1=2i−3j\) y\(v_2=4i+5j\).
Solución
\[\begin{align*} v_1+v_2 &= (2+4)i+(−3+5)j \\[4pt] &= 6i+2j \end{align*}\]
Cálculo de la Forma Componente de un Vector: Dirección
Hemos visto cómo dibujar vectores de acuerdo a sus puntos inicial y terminal y cómo encontrar el vector de posición. También hemos examinado la notación para vectores dibujados específicamente en el plano de coordenadas cartesianas usando\(i\) y\(j\). Para cualquiera de estos vectores, podemos calcular la magnitud. Ahora, queremos combinar los puntos clave, y mirar más a fondo las ideas de magnitud y dirección.
El cálculo de la dirección sigue el mismo proceso sencillo que usamos para las coordenadas polares. Encontramos la dirección del vector al encontrar el ángulo con respecto a la horizontal. Esto lo hacemos usando las identidades trigonométricas básicas, pero con el\(| v |\) reemplazo\(r\).
Dado un vector de posición\(v=⟨x,y⟩\) y un ángulo de dirección\(\theta\),
\[ \begin{align*} \cos \theta &= \dfrac{x}{|v|} \text{ and } \sin \theta=y|v| \\[4pt] x &= |v| \cos \theta \\[4pt] y &= |v| \sin \theta \end{align*}\]
Así,\(v=xi+yj=| v | \cos \theta i+| v | \sin \theta j\), y la magnitud se expresa como\(| v |=\sqrt{x^2+y^2}\).
Escribe un vector con longitud\(7\) en un ángulo del\(135°\) eje x positivo en términos de magnitud y dirección.
Solución
Usando las fórmulas de conversión\(x=| v | \cos \theta i\) y\(y=| v | \sin \theta j\), encontramos que
\[ \begin{align*} x &= 7\cos(135°)i \\[4pt] &= −\dfrac{7\sqrt{2}}{2} \\[4pt] y &=7 \sin(135°)j \\[4pt] &= \dfrac{7\sqrt{2}}{2} \end{align*}\]
Este vector puede escribirse\(v=7\cos(135°)i+7\sin(135°)j\) o simplificarse como
\(v=−\dfrac{7\sqrt{2}}{2}i+\dfrac{7\sqrt{2}}{2}j\)
Un vector viaja desde el origen hasta el punto\((3,5)\). Escribe el vector en términos de magnitud y dirección.
- Contestar
-
\(v=\sqrt{34}\cos(59°)i+\sqrt{34}\sin(59°)j\)
Magnitud =\(34\)
\(\theta={\tan}^{−1}\left(\dfrac{5}{3}\right)=59.04°\)
Encontrar el producto de punto de dos vectores
Como comentamos anteriormente en la sección, la multiplicación escalar implica multiplicar un vector por un escalar, y el resultado es un vector. Como hemos visto, multiplicar un vector por un número se llama multiplicación escalar. Si multiplicamos un vector por un vector, hay dos posibilidades: el producto punto y el producto cruzado. Aquí solo examinaremos el producto punto; puede encontrar el producto cruzado en cursos de matemáticas más avanzados.
El producto punto de dos vectores implica multiplicar dos vectores juntos, y el resultado es un escalar.
El punto producto de dos vectores\(v=⟨a,b⟩\) y\(u=⟨c,d⟩\) es la suma del producto de los componentes horizontales y el producto de los componentes verticales.
\[v⋅u=ac+bd\]
Para encontrar el ángulo entre los dos vectores, usa la siguiente fórmula.
\[\cos \theta=\dfrac{v}{| v |}⋅\dfrac{u}{| u |}\]
Encuentra el producto punto de\(v=⟨5,12⟩\) y\(u=⟨−3,4⟩\).
Solución
Usando la fórmula, tenemos
\[\begin{align*} v⋅u &= ⟨5,12⟩⋅⟨−3,4⟩ \\[4pt] &= 5⋅(−3)+12⋅4 \\[4pt] &= −15+48 \\[4pt] &= 33 \end{align*}\]
Encuentra el producto punto de\(v_1 = 5i + 2j\) y\(v_2 = 3i + 7j\). Después, encuentra el ángulo entre los dos vectores.
Solución
Al encontrar el producto punto, multiplicamos los componentes correspondientes.
\[ \begin{align*} v_1⋅v_2 &= ⟨5,2⟩⋅⟨3,7⟩ \\[4pt] &= 5⋅3+2⋅7 \\[4pt] &= 15+14 \\[4pt] &= 29 \end{align*}\]
Para encontrar el ángulo entre ellos, usamos la fórmula\(\cos \theta=\dfrac{v}{|v|}⋅\dfrac{u}{|u|}\).
\[\begin{align*} \dfrac{v}{|v|}\cdot \dfrac{u}{|u|} &= \left \langle \dfrac{5}{\sqrt{29}}+\dfrac{2}{\sqrt{29}} \right \rangle \cdot \left \langle \dfrac{3}{\sqrt{58}}+\dfrac{7}{\sqrt{58}} \right \rangle \\[4pt] &=\dfrac{5}{\sqrt{29}}\cdot \dfrac{3}{\sqrt{58}}+\dfrac{2}{\sqrt{29}}\cdot \dfrac{7}{\sqrt{58}} \\[4pt] &= \dfrac{15}{\sqrt{1682}}+\dfrac{14}{\sqrt{1682}}\\ &=\dfrac{29}{\sqrt{1682}} \\[4pt] &= 0.707107 \\[4pt] {\cos}^{-1}(0.707107) &= 45° \end{align*}\]
Ver Figura\(\PageIndex{18}\).
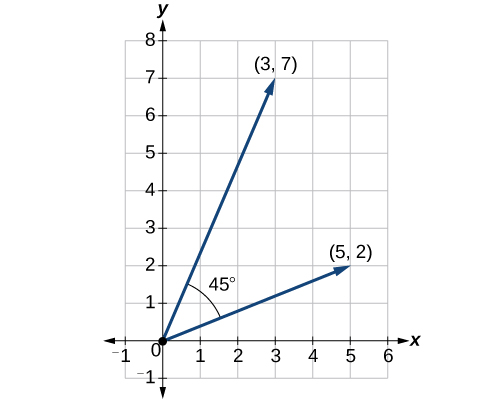
Figura\(\PageIndex{18}\)
Encuentra el ángulo entre\(u=⟨−3,4⟩\) y\(v=⟨5,12⟩\).
Solución
Usando la fórmula, tenemos
\[\begin{align*} \theta &= {\cos}^{−1}\left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) \\[4pt] \left(\dfrac{u}{|u|}⋅\dfrac{v}{|v|}\right) &= \dfrac{−3i+4j}{5}⋅\dfrac{5i+12j}{13} \\[4pt] &= \left(− \dfrac{3}{5}⋅ \dfrac{5}{13}\right)+\left(\dfrac{4}{5}⋅ \dfrac{12}{13}\right) \\[4pt] &= −\dfrac{15}{65}+\dfrac{48}{65} \\[4pt] &= \dfrac{33}{65} \\[4pt] \theta &= {\cos}^{−1}\left(\dfrac{33}{65}\right) \\[4pt] &= 59.5^{\circ} \end{align*}\]
Ver Figura\(\PageIndex{19}\).
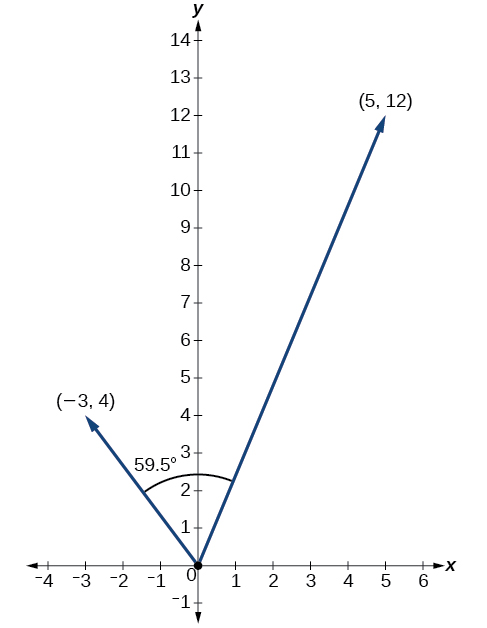
Figura\(\PageIndex{19}\)
Ahora tenemos las herramientas para resolver el problema que introdujimos en la apertura de la sección.
Un avión vuela a una velocidad aérea de\(200\) millas por hora con rumbo SE de\(140°\). Un viento del norte (de norte a sur) sopla a\(16.2\) millas por hora. ¿Cuál es la velocidad de avance y el rodamiento real del avión? Ver Figura\(\PageIndex{20}\).
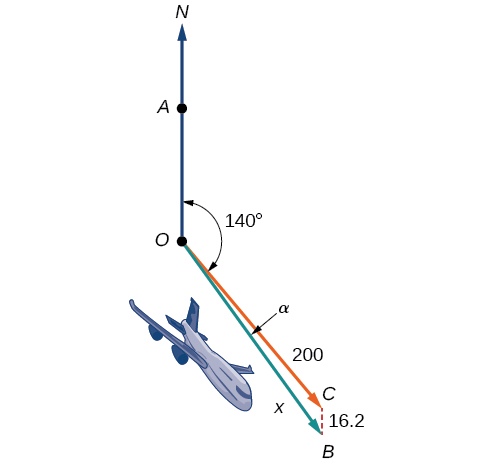
Figura\(\PageIndex{20}\)
Solución
La velocidad de avance está representada por\(x\) en el diagrama, y necesitamos encontrar el ángulo\(\alpha\) para poder calcular el rodamiento ajustado, que será\(140°+\alpha\).
Observe en la Figura\(\PageIndex{20}\), que el ángulo\(\angle BCO\) debe ser igual al ángulo\(\angle AOC\) por la regla de alternar ángulos interiores, por lo que el ángulo\(\angle BCO\) es 140°. Podemos encontrar\(x\) por la Ley de Cosinos:
\[\begin{align*} x^2 &= {(16.2)}^2+{(200)}^2−2(16.2)(200) \cos(140°) \\[4pt] x^2 &= 45,226.41 \\[4pt] x &= \sqrt{45,226.41} \\[4pt] x &= 212.7 \end{align*}\]
La velocidad sobre el suelo es de aproximadamente\(213\) millas por hora. Ahora podemos calcular el rodamiento usando la Ley de Sines.
\[\begin{align*} \dfrac{\sin \alpha}{16.2} &= \dfrac{\sin(140°)}{212.7} \\[4pt] \sin \alpha &= \dfrac{16.2 \sin(140°)}{212.7} \\[4pt] &=0.04896 \\[4pt] {\sin}^{−1}(0.04896) &= 2.8° \end{align*}\]
Por lo tanto, el avión tiene un rodamiento SE de\(140°+2.8°=142.8°\). La velocidad del suelo es de\(212.7\) millas por hora.
Conceptos clave
- El vector de posición tiene su punto inicial en el origen. Ver Ejemplo\(\PageIndex{1}\).
- Si el vector de posición es el mismo para dos vectores, son iguales. Ver Ejemplo\(\PageIndex{2}\).
- Los vectores se definen por su magnitud y dirección. Ver Ejemplo\(\PageIndex{3}\).
- Si dos vectores tienen la misma magnitud y dirección, son iguales. Ver Ejemplo\(\PageIndex{4}\).
- La suma y resta de vectores dan como resultado un nuevo vector que se encuentra sumando o restando los elementos correspondientes. Ver Ejemplo\(\PageIndex{5}\).
- La multiplicación escalar es multiplicar un vector por una constante. Sólo cambia la magnitud; la dirección permanece igual. Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
- Los vectores están compuestos por dos componentes: el componente horizontal a lo largo del\(x\) eje positivo y el componente vertical a lo largo del\(y\) eje positivo. Ver Ejemplo\(\PageIndex{8}\).
- El vector unitario en la misma dirección que cualquier vector distinto de cero se encuentra dividiendo el vector por su magnitud.
- La magnitud de un vector en el sistema de coordenadas rectangulares es\(| v |=\sqrt{a^2+b^2}\). Ver Ejemplo\(\PageIndex{9}\).
- En el sistema de coordenadas rectangulares, los vectores unitarios pueden representarse en términos de\(ii\) y\(jj\) donde\(i\) representa el componente horizontal y\(j\) representa el componente vertical. Entonces,\(v = ai + bj\) es un múltiplo escalar de\(v\) por números reales\(a\) y\(b\). Ver Ejemplo\(\PageIndex{10}\) y Ejemplo\(\PageIndex{11}\).
- Sumar y restar vectores en términos de\(i\) y\(j\) consiste en sumar o restar los coeficientes correspondientes de\(i\) y los coeficientes correspondientes de\(j\). Ver Ejemplo\(\PageIndex{12}\).
- Un vector\(v = ai + bj\) se escribe en términos de magnitud y dirección como\(v=| v |\cos \theta i+| v |\sin \theta j\). Ver Ejemplo\(\PageIndex{13}\).
- El producto punto de dos vectores es el producto de los\(i\) términos más el producto de los\(j\) términos. Ver Ejemplo\(\PageIndex{14}\).
- Podemos usar el producto punto para encontrar el ángulo entre dos vectores. Ejemplo\(\PageIndex{15}\) y Ejemplo\(\PageIndex{16}\).
- Los productos Dot son útiles para muchos tipos de aplicaciones de física. Ver Ejemplo\(\PageIndex{17}\).


