10.E: Geometría Analítica (Ejercicios)

10.1: La elipse

En esta sección, investigaremos la forma de esta sala y sus aplicaciones en el mundo real, incluyendo hasta qué punto de distancia pueden pararse dos personas en el Salón de Estatuas y aún se escuchan susurrar.

Verbal

1) Definir una elipse en términos de sus focos.

Responder

Una elipse es el conjunto de todos los puntos en el plano cuya suma de distancias desde dos puntos fijos, llamados los focos, es una constante.

2) ¿Dónde deben estar los focos de una elipse?

3) ¿Qué caso especial de elipse tenemos cuando los ejes mayor y menor son de la misma longitud?

Responder

Este caso especial sería un círculo.

4) Para el caso especial antes mencionado, ¿qué sería cierto de los focos de esa elipse?

5) ¿Qué se puede decir de la simetría de la gráfica de una elipse con centro en el origen y focos a lo largo del$y$ eje?

Responder

Es simétrico alrededor del$x$ eje -eje,$y$ -eje, y el origen.

Algebraico

Para los ejercicios 6-10, determinar si las ecuaciones dadas representan elipses. En caso afirmativo, escriba en forma estándar.

6)$2x^2 +y=4$

7)$4x^2 + 9y^2=36$

Responder

sí;$\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1$

8)$4x^2 - y^2=4$

9)$4x^2 + 9y^2=1$

Responder

sí;$\dfrac{x^2}{\left (\tfrac{1}{2} \right )^2}+\dfrac{y^2}{\left (\tfrac{1}{2} \right )^2}=1$

10)$4x^2-8x+9y^2-72y+112=0$

Para los ejercicios 11-26, escribir la ecuación de una elipse en forma estándar, e identificar los puntos finales de los ejes mayor y menor así como los focos.

11)$\dfrac{x^2}{4}+\dfrac{y^2}{49}=1$

Responder

$\dfrac{x^2}{2^2}+\dfrac{y^2}{7^2}=1$; Puntos finales del eje mayor$(0,7)$ y$(0,-7)$. Puntos finales de eje menor$(2,0)$ y$(-2,0)$. Focos en$(0, 3\sqrt{5})$,$(0, -3\sqrt{5})$.

12)$\dfrac{x^2}{100}+\dfrac{y^2}{64}=1$

13)$x^2 + 9y^2 = 1$

Responder

$\dfrac{x^2}{(1)^2}+\dfrac{y^2}{\left (\tfrac{1}{3} \right )^2}=1$; Puntos finales del eje mayor$(1,0)$ y$(-1,0)$. Puntos finales del eje menor$\left (0, \dfrac{1}{3} \right )$,$\left (0, -\dfrac{1}{3} \right )$. Focos en$\left (\dfrac{2\sqrt{2}}{3}, 0 \right )$,$\left (-\dfrac{2\sqrt{2}}{3}, 0 \right )$.

14)$4x^2 + 16y^2 = 1$

15)$\dfrac{(x-2)^2}{49}+\dfrac{(y-4)^2}{25}=1$

Responder

$\dfrac{(x-2)^2}{7^2}+\dfrac{(y-4)^2}{5^2}=1$; Puntos finales del eje mayor$(9,4)$,$(-5,4)$. Puntos finales del eje menor$(2,9)$,$(2,-1)$. Focos en$(2+2\sqrt{6}, 4)$,$(2-2\sqrt{6}, 4)$

16)$\dfrac{(x-2)^2}{81}+\dfrac{(y+1)^2}{16}=1$

17)$\dfrac{(x+5)^2}{4}+\dfrac{(y-7)^2}{9}=1$

Responder

$\dfrac{(x+5)^2}{2^2}+\dfrac{(y-7)^2}{3^2}=1$; Puntos finales del eje mayor$(-5,10)$,$(-5,4)$. Puntos finales del eje menor$(-3,7)$,$(-7,7)$. Focos en$(-5, 7+\sqrt{5})$,$(-5, 7-\sqrt{5})$

18)$\dfrac{(x-7)^2}{49}+\dfrac{(y-7)^2}{49}=1$

19)$4x^2-8x+9y^2-72y+112=0$

Responder

$\dfrac{(x-1)^2}{3^2}+\dfrac{(y-4)^2}{2^2}=1$; Puntos finales del eje mayor$(4,4)$,$(-2,4)$. Puntos finales del eje menor$(1,6)$,$(1,2)$. Focos en$(1+\sqrt{5}, 4)$,$(1-\sqrt{5}, 4)$

20)$9x^2-54x+9y^2-54y+81=0$

21)$4x^2-24x+36y^2-360y+864=0$

Responder

$\dfrac{(x-3)^2}{(3\sqrt{2})^2}+\dfrac{(y-5)^2}{\sqrt{2}^2}=1$; Puntos finales del eje mayor$(3+3\sqrt{2}, 5)$,$(3-3\sqrt{2}, 5)$. Puntos finales del eje menor$(3, 5+\sqrt{2})$,$(3, 5-\sqrt{2})$. Focos en$(7,5)$,$(-1,5)$

22)$4x^2+24x+16y^2-128y+228=0$

23)$4x^2+40x+25y^2-100y+100=0$

Responder

$\dfrac{(x+5)^2}{(5)^2}+\dfrac{(y-2)^2}{(2)^2}=1$; Puntos finales del eje mayor$(0,2)$,$(-10,2)$. Puntos finales del eje menor$(-5,4)$,$(-5,0)$. Focos en$(-5+\sqrt{21}, 2)$,$(-5-\sqrt{21}, 2)$

24)$x^2+2x+100y^2-1000y+2401=0$

25)$4x^2+24x+25y^2+200y+336=0$

Responder

$\dfrac{(x+3)^2}{(5)^2}+\dfrac{(y+4)^2}{(2)^2}=1$; Puntos finales del eje mayor$(2,-4)$,$(-8,-4)$. Puntos finales del eje menor$(-3,-2)$,$(-3,-6)$. Focos en$(-3+\sqrt{21}, -4)$,$(-3-\sqrt{21}, -4)$

26)$9x^2+72x+16y^2+16y+4=0$

Para los ejercicios 27-31, encuentra los focos para las elipses dadas.

27)$\dfrac{(x+3)^2}{25}+\dfrac{(y+1)^2}{36}=1$

Responder

Focos$(-3, -1+\sqrt{11})$,$(-3, -1-\sqrt{11})$

28)$\dfrac{(x+1)^2}{100}+\dfrac{(y-2)^2}{4}=1$

29)$x^2+y^2=1$

Responder

Enfoque$(0,0)$

30)$x^2+4y^2+4x+8y=1$

31)$10x^2+y^2+200x=0$

Responder

Focos$(-10,30)$,$(-10,-30)$

Gráfica

Para los ejercicios 32-45, grafica las elipses dadas, señalando el centro, los vértices y los focos.

32)$\dfrac{x^2}{25}+\dfrac{y^2}{36}=1$

33)$\dfrac{x^2}{16}+\dfrac{y^2}{9}=1$

Responder

Centro$(0,0)$, Vértices$(4,0)$,$(-4,0)$,$(0,3)$,$(0,-3)$. Focos$(\sqrt{7},0)$,$(-\sqrt{7},0)$

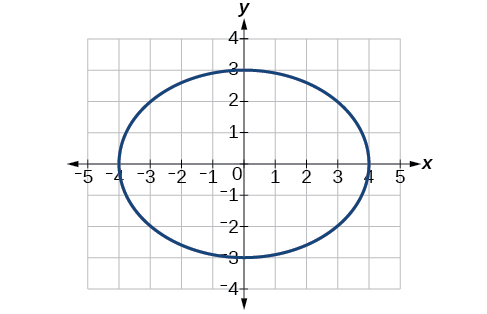
34)$4x^2+9y^2=1$

35)$81x^2+49y^2=1$

Responder

Centro$(0,0)$, Vértices$\left ( \dfrac{1}{9}, 0 \right )$,$\left ( -\dfrac{1}{9}, 0 \right )$,$\left ( 0, \dfrac{1}{7} \right )$,$\left ( 0, \dfrac{1}{7} \right )$. Focos$\left ( 0, \dfrac{4\sqrt{2}}{63} \right )$,$\left ( 0, -\dfrac{4\sqrt{2}}{63} \right )$

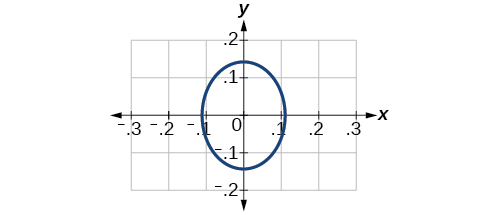
36)$\dfrac{(x-2)^2}{64}+\dfrac{(y-4)^2}{16}=1$

37)$\dfrac{(x+3)^2}{9}+\dfrac{(y-3)^2}{9}=1$

Responder

Centro$(-3,3)$, Vértices$(0,3)$,$(-6,3)$,$(-3,0)$,$(-3,6)$. Enfoque$(-3,3)$

Tenga en cuenta que esta elipse es un círculo. El círculo tiene un solo foco, que coincide con el centro.

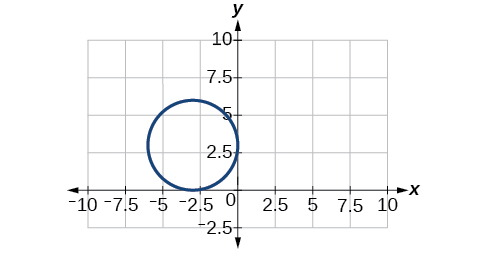
38)$\dfrac{x^2}{2}+\dfrac{(y+1)^2}{5}=1$

39)$4x^2-8x+16y^2-32y-44=0$

Responder

Centro$(1,1)$, Vértices$(5,1)$,$(-3,1)$,$(1,3)$,$(1,-1)$. Focos$(1,1+4\sqrt{3})$,$(1,1-4\sqrt{3})$

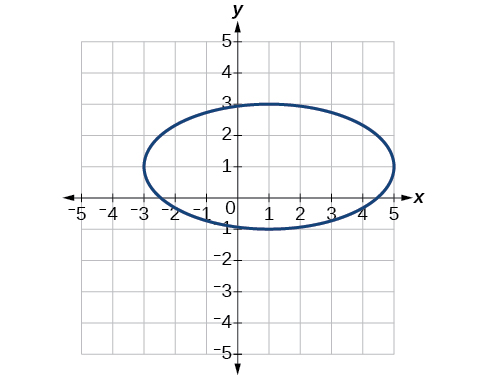
40)$x^2-8x+25y^2-100y+91=0$

41)$x^2+8x+4y^2-40y+112=0$

Responder

Centro$(-4,5)$, Vértices$(-2,5)$,$(-6,4)$,$(-4,6)$,$(-4,4)$. Focos$(-4+\sqrt{3}, 5)$,$(-4-4\sqrt{3}, 5)$

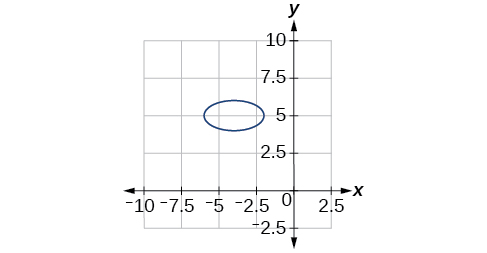
42)$64x^2+128x+9y^2-72y-368=0$

43)$16x^2+64x+4y^2-8y+4=0$

Responder

Centro$(-2,1)$, Vértices$(0,1)$,$(-4,1)$,$(-2,5)$,$(-2,-3)$. Focos$(-2,1+2\sqrt{3})$,$(-2,1-2\sqrt{3})$

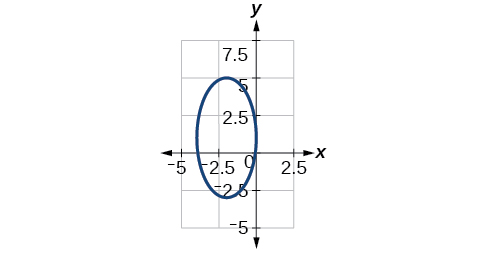
44)$100x^2+1000x+y^2-10y+2425=0$

45)$4x^2+16x+4y^2+16y+16=0$

Responder

Centro$(-2,2)$, Vértices$(0,-2)$,$(-4,-2)$,$(-2,0)$,$(-2,-4)$. Enfoque$(-2,-2)$

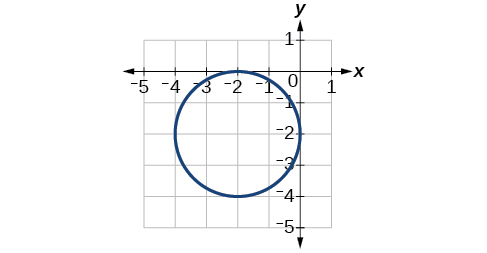
Para los ejercicios 46-51, utilice la información dada sobre la gráfica de cada elipse para determinar su ecuación.

46) Centrar en el origen, simétrico con respecto a los ejes$x$ - y$y$ -ejes, enfoque$(4,0)$ y punto sobre la gráfica$(0,3)$.

47) Centrar en el origen, simétrico con respecto a los ejes$x$ - y$y$ -ejes, enfoque$(0,-2)$ y punto sobre la gráfica$(5,0)$.

Responder

$\dfrac{x^2}{25}+\dfrac{y^2}{29}=1$

48) Centrar en el origen, simétrico con respecto a los ejes$x$ - y$y$ -ejes, enfoque en$(3,0)$, y eje mayor es dos veces más largo que el eje menor.

49) Centro$(4,2)$; vértice$(9,2)$; un foco:$(4+2\sqrt{6}, 2)$

Responder

$\dfrac{(x-4)^2}{25}+\dfrac{(y-2)^2}{1}=1$

50) Centro$(3,5)$; vértice$(3,11)$; un foco:$(3, 5+4\sqrt{2})$

51) Centro$(-3,4)$; vértice$(1,4)$; un foco:$(-3+2\sqrt{3}, 4)$

Responder

$\dfrac{(x+3)^2}{16}+\dfrac{(y-4)^2}{4}=1$

Para los ejercicios 52-56, dada la gráfica de la elipse, determinar su ecuación.

52)

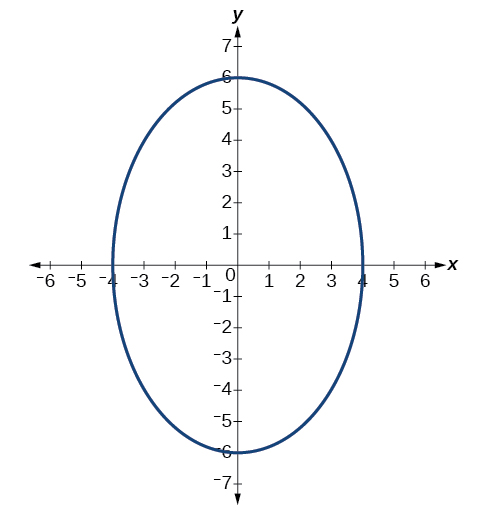
53)

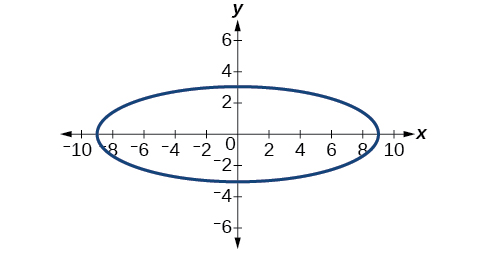
Responder

$\dfrac{x^2}{81}+\dfrac{y^2}{9}=1$

54)

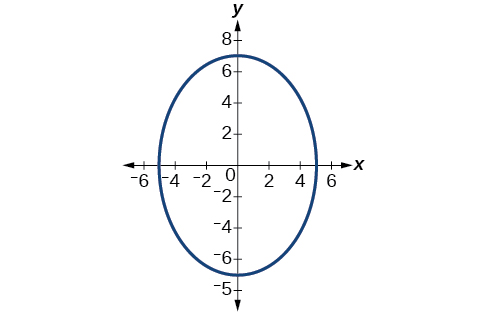
55)

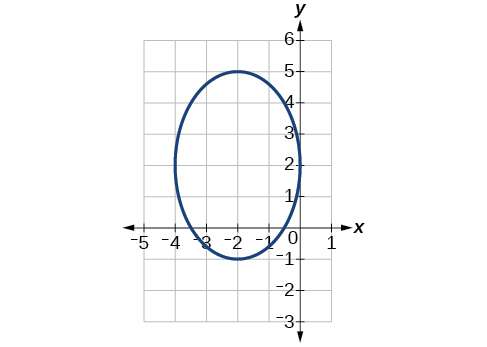
Responder

$\dfrac{(x+2)^2}{4}+\dfrac{(y-2)^2}{9}=1$

56)

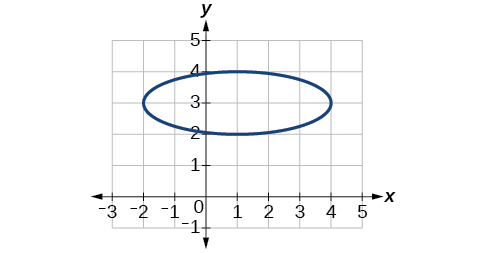
Extensiones

Para los ejercicios 57-61, encuentra el área de la elipse. El área de una elipse viene dada por la fórmula$\text {Area}=a\cdot b\cdot \pi$

57)$\dfrac{(x-3)^2}{9}+\dfrac{(y-3)^2}{16}=1$

Responder

$\text {Area} = 12\pi$unidades cuadradas

58)$\dfrac{(x+6)^2}{16}+\dfrac{(y-6)^2}{36}=1$

59)$\dfrac{(x+1)^2}{4}+\dfrac{(y-2)^2}{5}=1$

Responder

$\text {Area} = 2\sqrt{5} \pi$unidades cuadradas

60)$4x^2-8x+9y^2-72y+112=0$

61)$9x^2-54x+9y^2-54y+81=0$

Responder

$\text {Area} = 9\pi$unidades cuadradas

Aplicaciones del mundo real

62) Encuentra la ecuación de la elipse que solo cabrá dentro de una caja que sea$8$ unidades de ancho y$4$ unidades de alto.

63) Encuentra la ecuación de la elipse que solo cabrá dentro de una caja que es cuatro veces más ancha que alta. Expresar en términos de$h$, la altura.

Responder

$\dfrac{x^2}{4h^2}+\dfrac{y^2}{\tfrac{1}{4}h^2}=1$

64) Un arco tiene la forma de una semielipse (la mitad superior de una elipse). El arco tiene una altura de$8$ pies y un lapso de$20$ pies. Encuentra una ecuación para la elipse, y úsala para encontrar la altura al$0.01$ pie más cercano del arco a una distancia de$4$ pies del centro.

65) Un arco tiene la forma de una semielipse. El arco tiene una altura de$12$ pies y un lapso de$40$ pies. Encuentra una ecuación para la elipse, y úsala para encontrar la distancia desde el centro hasta un punto en el que la altura es$6$ pies. Redondear a la centésima más cercana.

Responder

$\dfrac{x^2}{400}+\dfrac{y^2}{144}=1$. Distancia =$17.32$ pies

66) Un puente se va a construir en forma de arco semielíptico y debe tener un tramo de$120$ pies. La altura del arco a una distancia de$40$ pies del centro es ser$8$ pies. Encuentra la altura del arco en su centro.

67) Una persona en una galería susurrante de pie en un foco de la elipse puede susurrar y ser escuchada por una persona parada en el otro foco porque todas las ondas sonoras que llegan al techo se reflejan a la otra persona. Si una galería susurrante tiene una longitud de$120$ pies, y los focos están ubicados a$30$ pies del centro, encuentra la altura del techo en el centro.

Responder

Aproximadamente$51.96$ pies

68) Una persona se encuentra a$8$ pies de la pared más cercana en una galería susurrante. Si esa persona está en un foco, y el otro enfoque está a$80$ pies de distancia, ¿cuál es la longitud y la altura en el centro de la galería?

10.2: La hipérbola

En geometría analítica, una hipérbola es una sección cónica formada por la intersección de un cono circular recto con un plano en un ángulo tal que ambas mitades del cono se intersectan. Esta intersección produce dos curvas independientes y no delimitadas que son imágenes especulares entre sí.

Verbal

1) Definir una hipérbola en términos de sus focos.

Responder

Una hipérbola es el conjunto de puntos en un plano cuya diferencia de distancias desde dos puntos fijos (focos) es una constante positiva.

2) ¿Qué podemos concluir sobre una hipérbola si sus asíntotas se cruzan en el origen?

3) ¿Qué debe ser cierto de los focos de una hipérbola?

Responder

Los focos deben estar en el eje transversal y estar en el interior de la hipérbola.

4) Si el eje transversal de una hipérbola es vertical, ¿qué sabemos de la gráfica?

5) ¿Dónde debe ser el centro de la hipérbola relativo a sus focos?

Responder

El centro debe ser el punto medio del segmento lineal que une los focos.

Algebraico

Para los ejercicios 6-10, determinar si las siguientes ecuaciones representan hipérbolas. Si es así, escriba en forma estándar.

6)$3y^2 + 2x = 6$

7)$\dfrac{x^2}{36}-\dfrac{y^2}{9}=1$

Responder

si$\dfrac{x^2}{6^2}-\dfrac{y^2}{3^2}=1$

8)$5y^2 + 4x^2 = 6x$

9)$25x^2 - 16y^2 = 400$

Responder

si$\dfrac{x^2}{4^2}-\dfrac{y^2}{5^2}=1$

10)$-9x^2+18x+y^2+4y-14=0$

Para los ejercicios 11-25, escribir la ecuación para la hipérbola en forma estándar si no es ya, e identificar los vértices y focos, y escribir ecuaciones de asíntotas.

11)$\dfrac{x^2}{25}-\dfrac{y^2}{36}=1$

Responder

$\dfrac{x^2}{5^2}-\dfrac{y^2}{6^2}=1$; vértices:$(5,0)$,$(-5,0)$; focos:$(\sqrt{61},0)$,$(-\sqrt{61},0)$; asíntotas:$y=\dfrac{6}{5}x$,$y=-\dfrac{6}{5}x$

12)$\dfrac{x^2}{100}-\dfrac{y^2}{9}=1$

13)$\dfrac{y^2}{4}-\dfrac{x^2}{81}=1$

Responder

$\dfrac{y^2}{2^2}-\dfrac{x^2}{9^2}=1$; vértices:$(0,2)$,$(0,-2)$; focos:$(0,\sqrt{85})$,$(0,-\sqrt{85})$; asíntotas:$y=\dfrac{2}{9}x$,$y=-\dfrac{2}{9}x$

14)$9y^2 - 4x^2 = 1$

15)$\dfrac{(x-1)^2}{9}-\dfrac{(y-2)^2}{16}=1$

Responder

$\dfrac{(x-1)^2}{3^2}-\dfrac{(y-2)^2}{4^2}=1$; vértices:$(4,2)$,$(-2,2)$; focos:$(6,2)$,$(-4,2)$; asíntotas:$y=\dfrac{4}{3}(x-1)+2$,$y=-\dfrac{4}{3}(x-1)+2$

16)$\dfrac{(y-6)^2}{36}-\dfrac{(x+1)^2}{16}=1$

17)$\dfrac{(x-2)^2}{49}-\dfrac{(y+7)^2}{49}=1$

Responder

$\dfrac{(x-2)^2}{7^2}-\dfrac{(y+7)^2}{7^2}=1$; vértices:$(9,-7)$,$(-5,-7)$; focos:$(2+7\sqrt{2},-7)$,$(2-7\sqrt{2},-7)$; asíntotas:$y=x-9$,$y=-x-5$

18)$4x^2-8x-9y^2-72y+112=0$

19)$-9x^2-54x+9y^2-54y+81=0$

Responder

$\dfrac{(x+3)^2}{3^2}-\dfrac{(y-3)^2}{3^2}=1$; vértices:$(0,3)$,$(-6,3)$; focos:$(-3+3\sqrt{2},1)$,$(-3-3\sqrt{2},1)$; asíntotas:$y=x+6$,$y=-x$

20)$4x^2-24x-36y^2-360y+864=0$

21)$-4x^2+24x+16y^2-128y+156=0$

Responder

$\dfrac{(y-4)^2}{2^2}-\dfrac{(x-3)^2}{4^2}=1$; vértices:$(3,6)$,$(3,2)$; focos:$(3,4+2\sqrt{5})$,$(3,4-2\sqrt{5})$; asíntotas:$y=\dfrac{1}{2}(x-3)+4$,$y=-\dfrac{1}{2}(x-3)+4$

22)$-4x^2+40x+25y^2-100y+100=0$

23)$x^2+2x-100y^2-1000y+2401=0$

Responder

$\dfrac{(y+5)^2}{7^2}-\dfrac{(x+1)^2}{70^2}=1$; vértices:$(-1,2)$,$(-1,-12)$; focos:$(-1,-5+7\sqrt{101})$,$(-1,-5-7\sqrt{101})$; asíntotas:$y=\dfrac{1}{10}(x+1)-5$,$y=-\dfrac{1}{10}(x+1)-5$

24)$-9x^2+72x+16y^2+16y+4=0$

25)$4x^2+24x-25y^2+200y-464=0$

Responder

$\dfrac{(x+3)^2}{5^2}-\dfrac{(y-4)^2}{2^2}=1$; vértices:$(2,4)$,$(-8,4)$; focos:$(-3+\sqrt{29},4)$,$(-3-\sqrt{29},4)$; asíntotas:$y=\dfrac{2}{5}(x+3)+4$,$y=-\dfrac{2}{5}(x+3)+4$

Para los ejercicios 26-30, encuentra las ecuaciones de las asíntotas para cada hipérbola.

26)$\dfrac{y^2}{3^2}-\dfrac{x^2}{3^2}=1$

27)$\dfrac{(x-3)^2}{5^2}-\dfrac{(y+4)^2}{2^2}=1$

Responder

$y=\dfrac{2}{5}(x-3)-4$,$y=-\dfrac{2}{5}(x-3)-4$

28)$\dfrac{(y-3)^2}{3^2}-\dfrac{(x+5)^2}{6^2}=1$

29)$9x^2-18x-16y^2+32y-151=0$

Responder

$y=\dfrac{3}{4}(x-1)+1$,$y=-\dfrac{3}{4}(x-1)+1$

30)$16y^2+96y-4x^2+16x+112=0$

Gráfica

Para los ejercicios 31-44, esbozar una gráfica de la hipérbola, etiquetando vértices y focos.

31)$\dfrac{x^2}{49}-\dfrac{y^2}{16}=1$

Responder

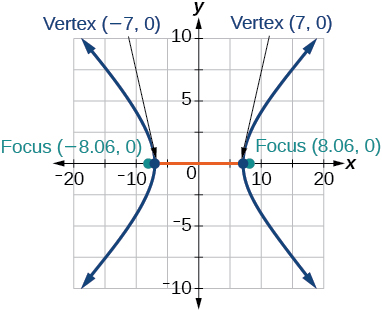
32)$\dfrac{x^2}{64}-\dfrac{y^2}{4}=1$

33)$\dfrac{y^2}{9}-\dfrac{x^2}{25}=1$

Responder

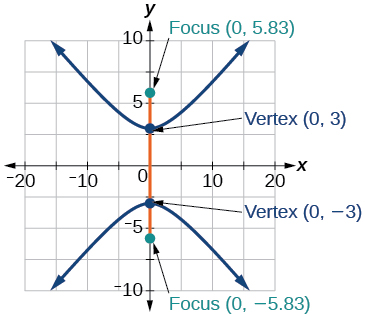
34)$81x^2-9y^2=1$

35)$\dfrac{(y+5)^2}{9}-\dfrac{(x-4)^2}{25}=1$

Responder

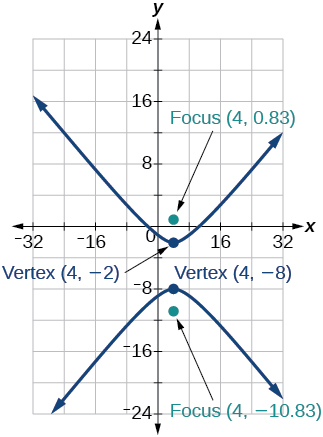
36)$\dfrac{(x-2)^2}{8}-\dfrac{(y+3)^2}{27}=1$

37)$\dfrac{(y-3)^2}{9}-\dfrac{(x-3)^2}{9}=1$

Responder

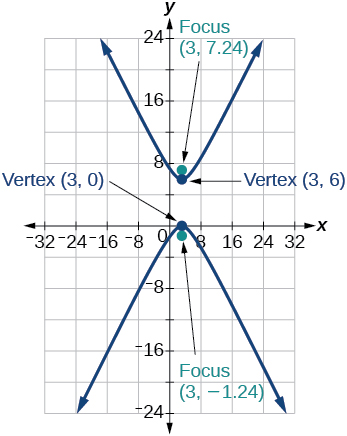
38)$-4x^2-8x+16y^2-32y-52=0$

39)$x^2-8x-25y^2-100y-109=0$

Responder

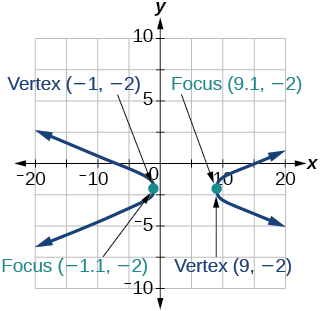
40)$-x^2+8x+4y^2-40y+88=0$

41)$64x^2+128x-9y^2-72y-656=0$

Responder

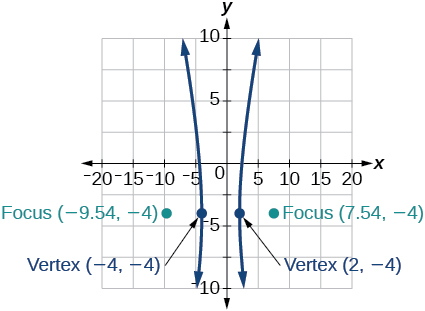
42)$16x^2+64x-4y^2-8y-4=0$

43)$-100x^2+1000x+y^2-10y-2575=0$

Responder

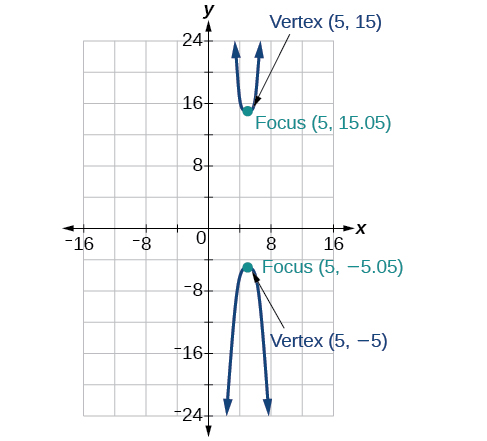
44)$4x^2+16x-4y^2+16y+16=0$

Para los ejercicios 45-50, dada información sobre la gráfica de la hipérbola, encuentra su ecuación.

45) Vértices en$(3,0)$ y$(-3,0)$ y un enfoque en$(5,0)$.

Responder

$\dfrac{x^2}{9}-\dfrac{y^2}{16}=1$

46) Vértices en$(0,6)$ y$(0,-6)$ y un enfoque en$(0,-8)$.

47) Vértices en$(1,1)$ y$(11,1)$ y un enfoque en$(12,1)$.

Responder

$\dfrac{(x-6)^2}{25}-\dfrac{(y-1)^2}{11}=1$

48) Centro:$(0,0)$; vértice:$(0,-13)$;un enfoque:$(0,\sqrt{313})$.

49) Centro:$(4,2)$; vértice:$(9,2)$;un enfoque:$(4+\sqrt{26},2)$.

Responder

$\dfrac{(x-4)^2}{25}-\dfrac{(y-2)^2}{1}=1$

50) Centro:$(3,5)$; vértice:$(3,11)$; un foco:$(3,5+2\sqrt{10})$.

Para los ejercicios 51-,55 dada la gráfica de la hipérbola, encuentra su ecuación.

51)

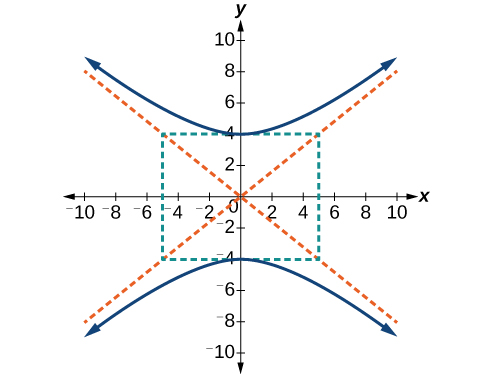
Responder

$\dfrac{y^2}{16}-\dfrac{x^2}{25}=1$

52)

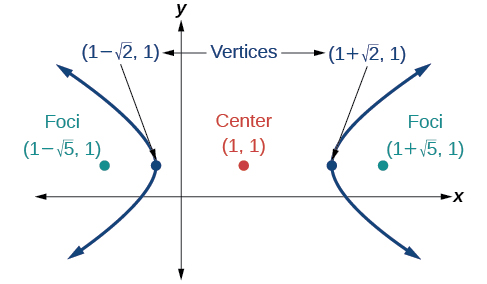
53)

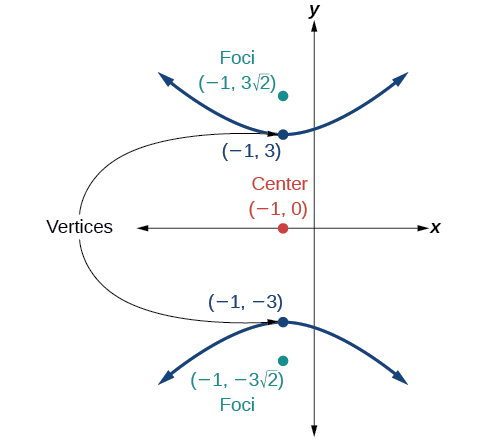
Responder

$\dfrac{y^2}{9}-\dfrac{(x+1)^2}{9}=1$

54)

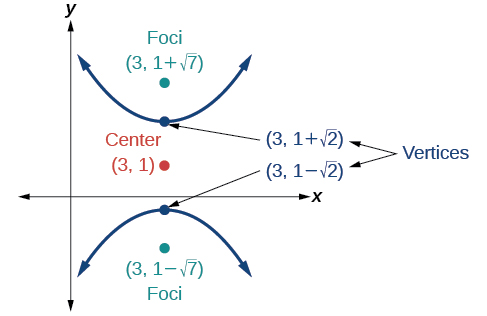
55)

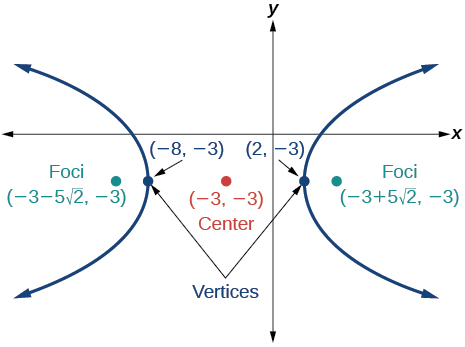
Responder

$\dfrac{(x+3)^2}{25}-\dfrac{(y+3)^2}{25}=1$

Extensiones

Para los ejercicios 56-60, expresar la ecuación para la hipérbola como dos funciones, con$y$ como una función de$x$. Exprese de la manera más sencilla posible. Utilice una calculadora gráfica para bosquejar la gráfica de las dos funciones en los mismos ejes.

56)$\dfrac{x^2}{4}-\dfrac{y^2}{9}=1$

57)$\dfrac{y^2}{9}-\dfrac{x^2}{1}=1$

Responder

$y(x)=3\sqrt{x^2 +1}$,$y(x)=-3\sqrt{x^2 +1}$

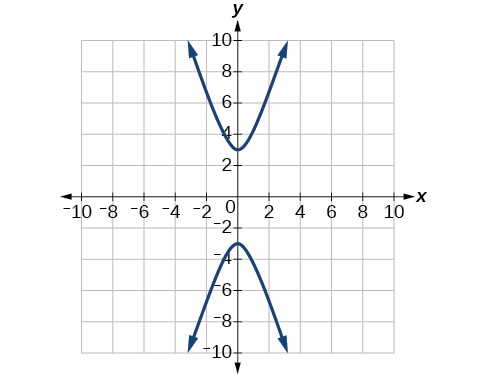
58)$\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{25}=1$

59)$-4x^2-16x+y^2-2y-19=0$

Responder

$y(x)=1+2\sqrt{x^2 +4x+5}$,$y(x)=1-2\sqrt{x^2 +4x+5}$

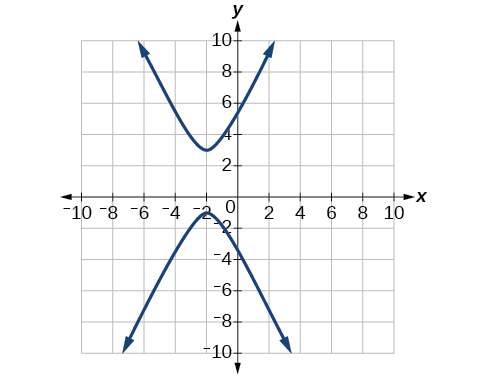
60)$4x^2-24x-y^2-4y+16=0$

Aplicaciones del mundo real

Para los ejercicios 61-65, se va a construir un seto en forma de hipérbola cerca de una fuente en el centro del patio. Encuentra la ecuación de la hipérbola y dibuja la gráfica.

61) El seto seguirá a las asíntotas$y=x$ y$y=-x$, y su distancia más cercana a la fuente central es de$5$ yardas.

Responder

$\dfrac{x^2}{25}-\dfrac{y^2}{25}=1$

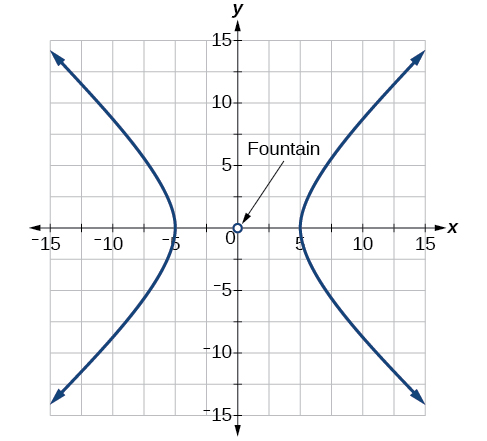
62) El seto seguirá a las asíntotas$y=2x$ y$y=-2x$, y su distancia más cercana a la fuente central es de$6$ yardas.

63) El seto seguirá a las asíntotas$y=\dfrac{1}{2}x$ y$y=-\dfrac{1}{2}x$, y su distancia más cercana a la fuente central es de$10$ yardas.

Responder

$\dfrac{x^2}{100}-\dfrac{y^2}{25}=1$

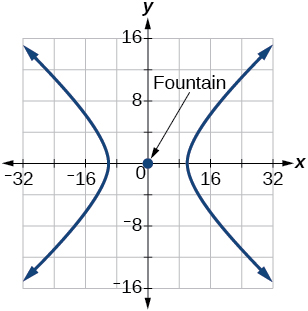
64) El seto seguirá a las asíntotas$y=\dfrac{2}{3}x$ y$y=-\dfrac{2}{3}x$, y su distancia más cercana a la fuente central es de$12$ yardas.

65) El seto seguirá a las asíntotas$y=\dfrac{3}{4}x$ y$y=-\dfrac{3}{4}x$, y su distancia más cercana a la fuente central es de$20$ yardas.

Responder

$\dfrac{x^2}{400}-\dfrac{y^2}{225}=1$

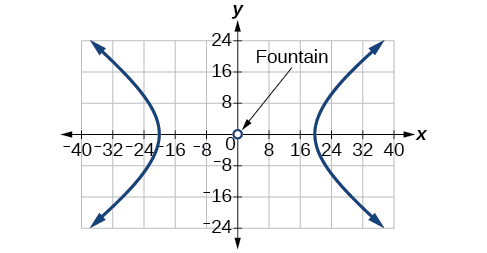
Para los ejercicios 66-70, supongamos que un objeto entra en nuestro sistema solar y queremos graficar su trayectoria en un sistema de coordenadas con el sol en el origen y el$x$ eje -eje como eje de simetría para la trayectoria del objeto. Dar la ecuación de la trayectoria de vuelo de cada objeto utilizando la información dada.

66) El objeto entra por un camino aproximado por la línea$y=x-2$ y pasa dentro de$1$ au (unidad astronómica) del sol en su aproximación más cercana, de manera que el sol es uno de los focos de la hipérbola. Luego sale del sistema solar a lo largo de un camino aproximado por la línea$y=−x+2$.

67) El objeto entra por un camino aproximado por la línea$y=2x-2$ y pasa dentro de$0.5$ au del sol en su aproximación más cercana, por lo que el sol es uno de los focos de la hipérbola. Luego sale del sistema solar a lo largo de un camino aproximado por la línea$y=-2x+2$.

Responder

$\dfrac{(x-1)^2}{0.25}-\dfrac{y^2}{0.75}=1$

68) El objeto entra por un camino aproximado por la línea$y=0.5x+2$ y pasa dentro de$1$ au del sol en su aproximación más cercana, por lo que el sol es uno de los focos de la hipérbola. Luego sale del sistema solar a lo largo de un camino aproximado por la línea$y=−0.5x−2$.

69) El objeto entra por un camino aproximado por la línea$y=\dfrac{1}{3}x-1$ y pasa dentro de$1$ au del sol en su aproximación más cercana, por lo que el sol es uno de los focos de la hipérbola. Luego sale del sistema solar a lo largo de un camino aproximado por la línea$y=-\dfrac{1}{3}x+1$.

Responder

$(x-3)^2 - 9y^2 = 4$

70) El objeto entra por un camino aproximado por la línea$y=3x-9$ y pasa dentro de$1$ au del sol en su aproximación más cercana, por lo que el sol es uno de los focos de la hipérbola. Luego sale del sistema solar a lo largo de un camino aproximado por la línea$y=−3x+9$.

10.3: La Parábola

Al igual que la elipse y la hipérbola, la parábola también se puede definir por un conjunto de puntos en el plano de coordenadas. Una parábola es el conjunto de todos los puntos en un plano que están a la misma distancia de una línea fija, llamada directrix, y un punto fijo (el foco) no en la directrix.

Verbal

1) Definir una parábola en términos de su enfoque y directrix.

Responder

Una parábola es el conjunto de puntos en el plano que se encuentran equidistantes de un punto fijo, el foco, y una línea fija, la directriz.

2) Si la ecuación de una parábola está escrita en forma estándar y$p$ es positiva y la directrix es una línea vertical, entonces ¿qué podemos concluir sobre su gráfica?

3) Si la ecuación de una parábola está escrita en forma estándar y$p$ es negativa y la directrix es una línea horizontal, entonces ¿qué podemos concluir sobre su gráfica?

Responder

El gráfico se abrirá hacia abajo.

4) ¿Cuál es el efecto en la gráfica de una parábola si su ecuación en forma estándar tiene valores crecientes de$p$?

5) A medida que se ensancha la gráfica de una parábola, ¿qué pasará con la distancia entre el foco y la directriz?

Responder

La distancia entre el foco y la directrix aumentará.

Algebraico

Para los ejercicios 6-10, determinar si la ecuación dada es una parábola. Si es así, reescriba la ecuación en forma estándar.

6)$y^2=4-x^2$

7)$y=4x^2$

Responder

si$y=4(1)x^2$

8)$3x^2-6y^2=12$

9)$(y-3)^2=8(x-2)$

Responder

si$(y-3)^2=4(2)(x-2)$

10)$y^2+12x-6y-51=0$

Para los ejercicios 11-30, reescriba la ecuación dada en forma estándar, y luego determine el vértice$(V)$$(F)$, enfoque y directrix$(d)$ de la parábola.

11)$x=8y^2$

Responder

$y^2=\dfrac{1}{8}x$,$V:(0,0)$,$F:\left (\dfrac{1}{32},0 \right )$,$d:x=-\dfrac{1}{32}$

12)$y=\dfrac{1}{4}x^2$

13)$y=-4x^2$

Responder

$x^2=-\dfrac{1}{4}y$,$V:(0,0)$,$F:\left (0,-\dfrac{1}{16} \right )$,$d:y=-\dfrac{1}{16}$

14)$x=\dfrac{1}{8}y^2$

15)$x=36y^2$

Responder

$y^2=\dfrac{1}{36}x$,$V:(0,0)$,$F:\left (\dfrac{1}{144},0 \right )$,$d:x=-\dfrac{1}{144}$

16)$x=\dfrac{1}{36}y^2$

17)$(x-1)^2=4(y-1)$

Responder

$(x-1)^2=4(y-1)$,$V:(1,1)$,$F:(1,2)$,$d:y=0$

18)$(y-2)^2=\dfrac{4}{5}(x+4)$

19)$(y-4)^2=2(x+3)$

Responder

$(y-4)^2=2(x+3)$,$V:(-3,4)$,$F:\left (-\dfrac{5}{2},4 \right )$,$d:x=-\dfrac{7}{2}$

20)$(x+1)^2=2(y+4)$

21)$(x+4)^2=24(y+1)$

Responder

$(x+4)^2=24(y+1)$,$V:(-4,-1)$,$F:(-4,5)$,$d:y=-7$

22)$(y+4)^2=16(x+4)$

23)$y^2+12x-6y+21=0$

Responder

$(y-3)^2=-12(x+1)$,$V:(-1,3)$,$F:(-4,3)$,$d:x=2$

24)$x^2-4x-24y+28=0$

25)$5x^2-50x-4y+113=0$

Responder

$(x-5)^2=\dfrac{4}{5}(y+3)$,$V:(5,-3)$,$F:\left (5,-\dfrac{14}{5} \right )$,$d:y=-\dfrac{16}{5}$

26)$y^2-24x+4y-68=0$

27)$x^2-4x+2y-6=0$

Responder

$(x-2)^2=-2(y-5)$,$V:(2,5)$,$F:\left (2,\dfrac{9}{2} \right )$,$d:y=\dfrac{11}{2}$

28)$y^2-6y+12x-3=0$

29)$3y^2-4x-6y+23=0$

Responder

$(y-1)^2=\dfrac{4}{3}(x-5)$,$V:(5,1)$,$F:\left (\dfrac{16}{3},1 \right )$,$d:x=\dfrac{14}{3}$

30)$x^2+4x+8y-4=0$

Gráfica

Para los ejercicios 31-44, grafica la parábola, etiquetando el foco y la directriz.

31)$x=\dfrac{1}{8}y^2$

Responder

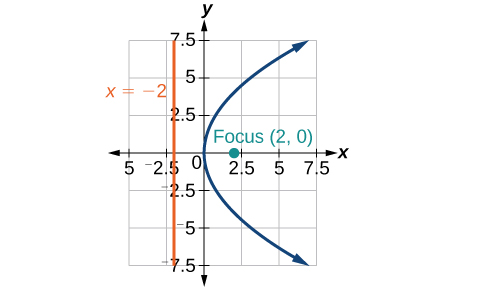
32)$y=36x^2$

33)$y=\dfrac{1}{36}x^2$

Responder

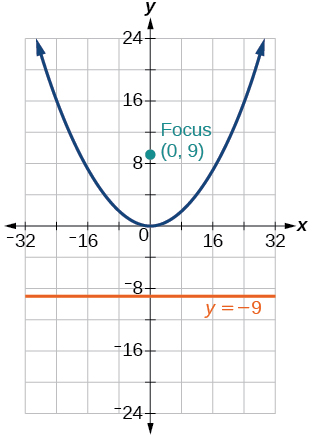
34)$y=-9x^2$

35)$(y-2)^2=-\dfrac{4}{3}(x+2)$

Responder

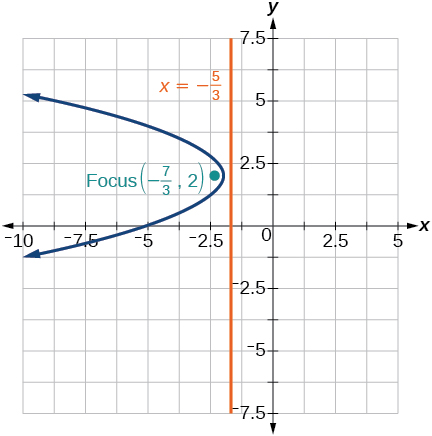
36)$-5(x+5)^2=4(y+5)$

37)$-6(y+5)^2=4(x-4)$

Responder

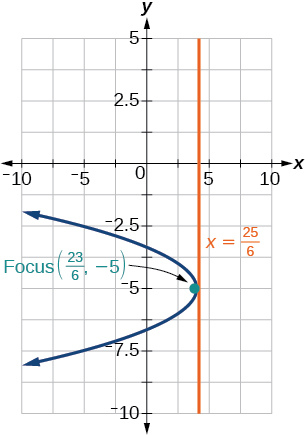
38)$y^2-6y-8x+1=0$

39)$x^2+8x+4y+20=0$

Responder

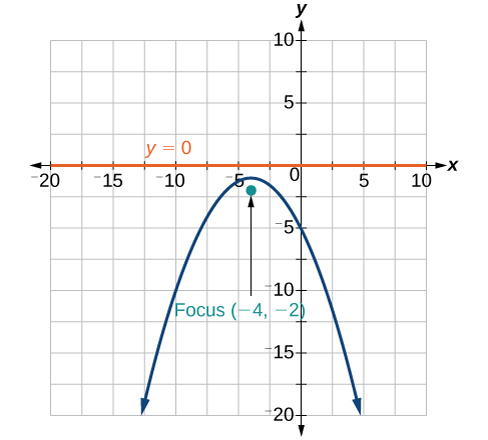
40)$3x^2+30x-4y+95=0$

41)$y^2-8x+10y+9=0$

Responder

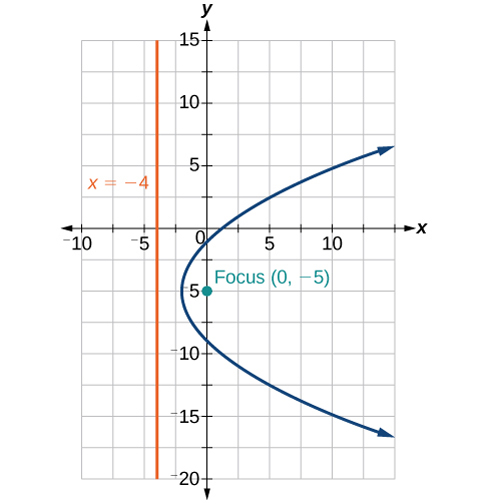
42)$x^2+4x+2y+2=0$

43)$y^2+2y-12x+61=0$

Responder

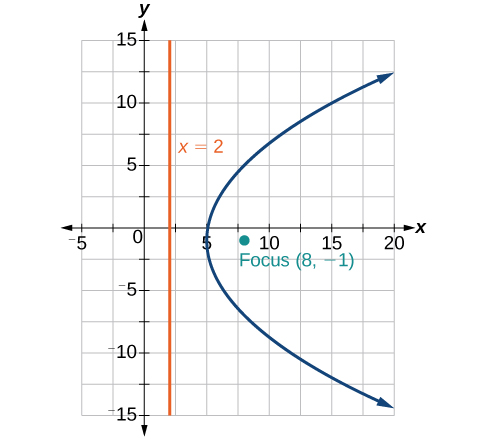
44)$-2x^2+8x-4y-24=0$

Para los ejercicios 45-50, encuentra la ecuación de la parábola dada información sobre su gráfica.

45) El vértice es$(0,0)$; directrix es$y=4$, el foco es$(0,-4)$.

Responder

$x^2=-16y$

46) El vértice es$(0,0)$; directrix es$x=4$, el foco es$(-4,0)$.

47) El vértice es$(2,2)$; directrix es el$x=2-\sqrt{2}$, foco es$(2+\sqrt{2},2)$.

Responder

$(y-2)^2 = 4\sqrt{2}(x-2)$

48) El vértice es$(-2,3)$; directrix es$x=-\dfrac{7}{2}$, el foco es$\left(-\dfrac{1}{2},3 \right)$.

49) El vértice es$(\sqrt{2},-\sqrt{3})$; directrix es$x=2\sqrt{2}$, el foco es$(0,-\sqrt{3})$.

Responder

$(y+\sqrt{3})^2 = -4\sqrt{2}(x-\sqrt{2})$

50) El vértice es$(-,21)$; directrix es$y=\dfrac{11}{3}$, el foco es$\left(1,\dfrac{1}{3} \right)$.

Para los ejercicios 51-55, determinar la ecuación para la parábola a partir de su gráfica.

51)

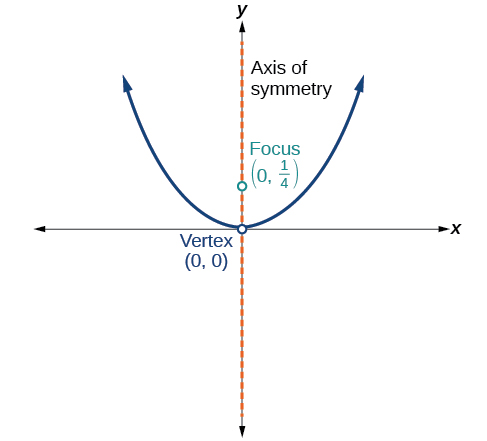
Responder

$x^2=y$

52)

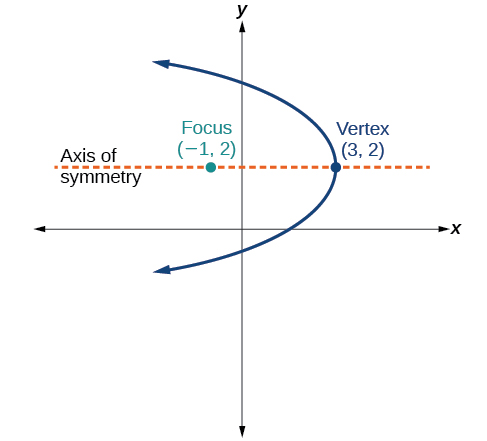
53)

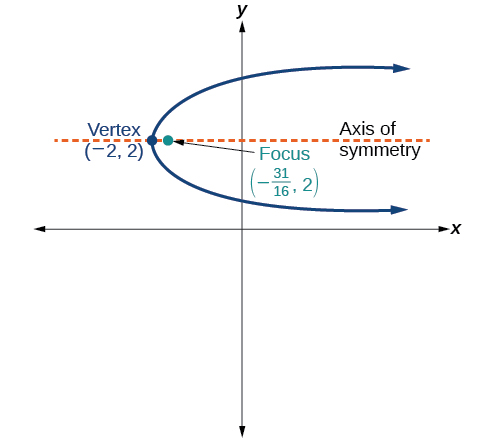
Responder

$(y-2)^2 = \dfrac{1}{4}(x+2)$

54)

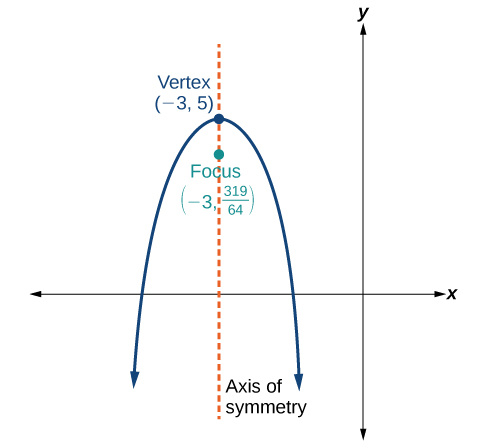
55)

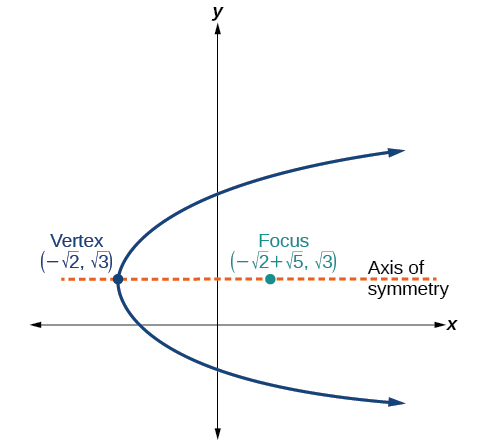
Responder

$(y-\sqrt{2})^2 = 4\sqrt{5}(x+\sqrt{2})$

Extensiones

Para los ejercicios 56-60, se dan el vértice y los puntos finales del recto latus de una parábola. Encuentra la ecuación.

56)$V(0,0)$, Puntos finales$(2,1),(−2,1)$

57)$V(0,0)$, puntos finales$(-2,4),(−2,-4)$

Responder

$y^2=-8x$

58)$V(1,2)$, Endpoints $(-5,5),(7,5)$

59)$V(-3,-1)$, Endpoints $(0,5),(0,-7)$

Responder

$(y+1)^2 = 12(x+3)$

60)$V(4,-3)$, Endpoints $\left ( 5,-\dfrac{7}{2} \right ), \left ( 3,-\dfrac{7}{2} \right )$

Aplicaciones del mundo real

61) El espejo en un faro de automóvil tiene una sección transversal parabólica con la bombilla en el foco. En un esquema, la ecuación de la parábola se da como$x^2=4y$. ¿En qué coordenadas debes colocar la bombilla?

Responder

$(0,1)$

62) Si queremos construir el espejo a partir del ejercicio anterior de tal manera que el foco se ubique en$(0,0.25)$ ¿cuál debería ser la ecuación de la parábola?

63) Una antena parabólica tiene la forma de un paraboloide de revolución. Esto significa que se puede formar girando una parábola alrededor de su eje de simetría. El receptor se ubicará en el foco. Si el plato tiene$12$ pies de ancho en su abertura y$4$ pies profundos en su centro, ¿dónde debe colocarse el receptor?

Responder

En el punto$2.25$ pies por encima del vértice.

64) Considerar la antena parabólica del ejercicio anterior. Si el platillo tiene$8$ pies de ancho en la abertura y$2$ pies de profundidad, ¿dónde debemos colocar el receptor?

65) Un foco de luz tiene la forma de un paraboloide de revolución. Una fuente de luz se encuentra a$1$ pie de la base a lo largo del eje de simetría. Si la apertura del foco es de$3$ pies de ancho, encuentra la profundidad.

Responder

$0.5625$pies

66) Si el foco del ejercicio anterior tiene la fuente de luz ubicada a$6$ centímetros de la base a lo largo del eje de simetría y la abertura es$4$ pies, encuentra la profundidad.

67) Un arco tiene forma de parábola. Tiene un lapso de$100$ pies y una altura máxima de$20$ pies. Encuentra la ecuación de la parábola, y determina la altura de los$40$ pies del arco desde el centro.

Responder

$x^2=-125(y-20)$, la altura es$7.2$ pies

68) Si el arco del ejercicio anterior tiene un lapso de$160$ pies y una altura máxima de$40$ pies, encuentre la ecuación de la parábola, y determine la distancia desde el centro a la que la altura es$20$ pies.

69) Se proyecta un objeto para seguir una trayectoria parabólica dada por$y=-x^2+96x$ dónde$x$ está la distancia horizontal recorrida en pies y$y$ es la altura. Determinar la altura máxima que alcanza el objeto.

Responder

$2304$pies

70) Para el objeto del ejercicio anterior, supongamos que la ruta seguida viene dada por$y=-0.5x^2+80x$. Determinar a lo largo de la horizontal viajó el objeto para alcanzar la altura máxima.

10.4: Rotación de Ejes

En secciones anteriores de este capítulo, nos hemos centrado en las ecuaciones de forma estándar para secciones cónicas no degeneradas. En esta sección, desplazaremos nuestro enfoque hacia la ecuación de forma general, que puede ser utilizada para cualquier cónica. La forma general se establece igual a cero, y los términos y coeficientes se dan en un orden particular, como se muestra a continuación.

Verbal

1) ¿Qué efecto tiene el$xy$ término en la gráfica de una sección cónica?

Responder

El$xy$ término provoca que se produzca una rotación de la gráfica.

2) Si la ecuación de una sección cónica está escrita en la forma$Ax^2+By^2+Cx+Dy+E=0$ y$AB=0$ ¿qué podemos concluir?

3) Si la ecuación de una sección cónica está escrita en la forma$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$, y$B^2-4AC>0$, ¿qué podemos concluir?

Responder

La sección cónica es una hipérbola.

4) Dada la ecuación$ax^2+4x+3y^2-12=0$, ¿qué podemos concluir si$a>0$?

5) Para la ecuación\(Ax^2+Bxy+Cy^2+Dx+Ey+F=0\) el valor de$\theta$ que satisface nos$\cot (2\theta )=\dfrac{A-C}{B}$ da ¿qué información?

Responder

Da el ángulo de rotación de los ejes para eliminar el$xy$ término.

Algebraico

Para los ejercicios 6-17, determinar qué sección cónica se representa con base en la ecuación dada.

6)$9x^2+4y^2+72x+36y-500=0$

7)$x^2-10x+4y-10=0$

Responder

$AB=0$, parábola

8)$2x^2-2y^2+4x-6y-2=0$

9)$4x^2-y^2+8x-1=0$

Responder

$AB=-4<0$, hipérbola

10)$4y^2-5x+9y+1=0$

11)$2x^2+3y^2-8x-12y+2=0$

Responder

$AB=6>0$, elipse

12)$4x^2+9xy+4y^2-36y-125=0$

13)$3x^2+6xy+3y^2-36y-125=0$

Responder

$B^2 - 4AC=0$, parábola

14)$-3x^2+3\sqrt{3}xy-4y^2+9=0$

15)$2x^2+4\sqrt{3}xy+6y^2-6x-3=0$

Responder

$B^2 - 4AC=0$, parábola

16)$-x^2+4\sqrt{2}xy+2y^2-2y+1=0$

17)$8x^2+4\sqrt{2}xy+4y^2-10x+1=0$

Responder

$B^2 - 4AC=-96<0$, elipse

Para los ejercicios 18-22, encontrar una nueva representación de la ecuación dada después de rotar a través del ángulo dado.

18)$3x^2+xy+3y^2-5=0, \theta =45^{\circ}$

19)$4x^2-xy+4y^2-2=0, \theta =45^{\circ}$

Responder

$7x'^2+9y'^2-4=0$

20)$2x^2+8xy-1=0, \theta =30^{\circ}$

21)$-2x^2+8xy+1=0, \theta =45^{\circ}$

Responder

$3x'^2+2x'y'-5y'^2+1=0$

22)$4x^2+\sqrt{2}xy+4y^2+y+2=0, \theta =45^{\circ}$

Para los ejercicios 23-30, determinar el ángulo$\theta$ que eliminará el$xy$ término y escribir la ecuación correspondiente sin el$xy$ término.

23)$x^2+3\sqrt{3}xy+4y^2+y-2=0$

Responder

$\theta =60^{\circ},11x'^2-y'2+\sqrt{3}x'+y'-4=0$

24)$4x^2+2\sqrt{3}xy+6y^2+y-2=0$

25)$9x^2-3\sqrt{3}xy+6y^2+4y-3=0$

Responder

$\theta =150^{\circ},21x'^2+9y'^2+4x'-4\sqrt{3}y'-6=0$

26)$-3x^2-\sqrt{3}xy-2y^2-x=0$

27)$16x^2+24xy+9y^2+6x-6y+2=0$

Responder

$\theta \approx 36.9^{\circ},125x'^2+6x'-42y'+10=0$

28)$x^2+4xy+4y^2+3x-2=0$

29)$x^2+4xy+y^2-2x+1=0$

Responder

$\theta =45^{\circ},3x'^2-y'^2-\sqrt{2}x'+\sqrt{2}y'+1=0$

30)$4x^2-2\sqrt{3}xy+6y^2-1=0$

Gráfica

Para los ejercicios 31-38, rote a través del ángulo dado con base en la ecuación dada. Dar la nueva ecuación y graficar la ecuación original y rotada.

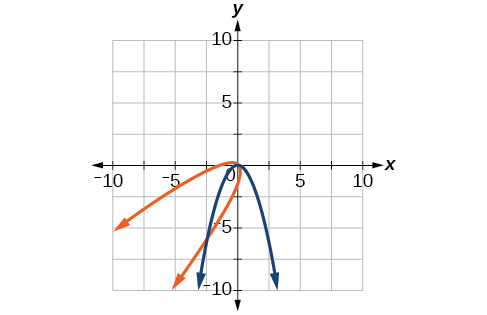
31)$y=-x^2,\theta =-45^{\circ}$

Responder

$\dfrac{\sqrt{2}}{2}(x'+y')=\dfrac{1}{2}(x'-y')^2$

32)$x=y^2,\theta =45^{\circ}$

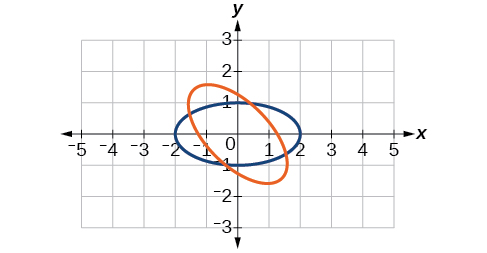
33)$\dfrac{x^2}{4}+\dfrac{y^2}{1}=1,\theta =45^{\circ}$

Responder

$\dfrac{(x'-y')^2}{8}+\dfrac{(x'+y')^2}{2}=1$

34)$\dfrac{y^2}{16}+\dfrac{x^2}{9}=1,\theta =45^{\circ}$

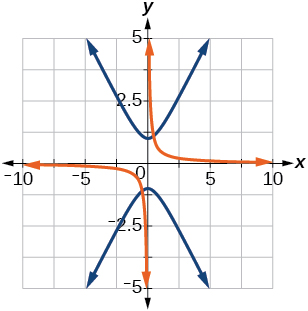
35)$y^2 - x^2 = 1, \theta =45^{\circ}$

Responder

$\dfrac{(x'+y')^2}{2}-\dfrac{(x'-y')^2}{2}=1$

36)$y=\dfrac{x^2}{2}, \theta =30^{\circ}$

37)$x=(y-1)^2, \theta =30^{\circ}$

Responder

$\dfrac{\sqrt{3}}{2}x'-\dfrac{1}{2}y'=\left ( \dfrac{1}{2}x' + \dfrac{\sqrt{3}}{2}x' - 1 \right )^2$

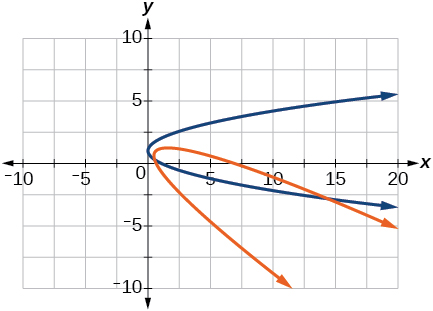
38)$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1,\theta =30^{\circ}$

Para los ejercicios 39-49, grafica la ecuación relativa al$x'y'$ sistema en el que la ecuación no tiene$x'y'$ término.

39)$xy=9$

Responder

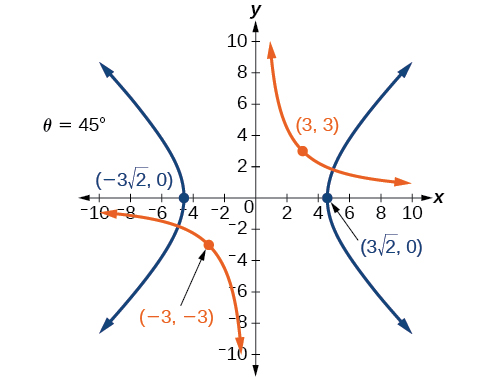
40)$x^2+10xy+y^2-6=0$

41)$x^2-10xy+y^2-24=0$

Responder

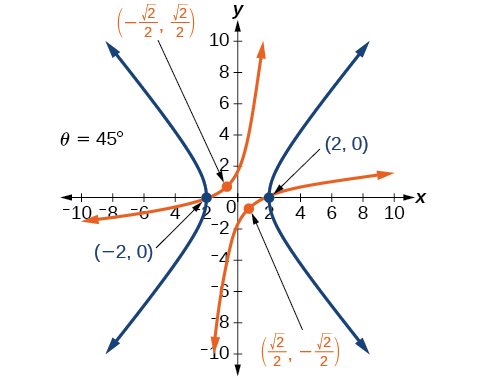
42)$4x^2-3\sqrt{3}xy+y^2-22=0$

43)$6x^2+2\sqrt{3}xy+4y^2-21=0$

Responder

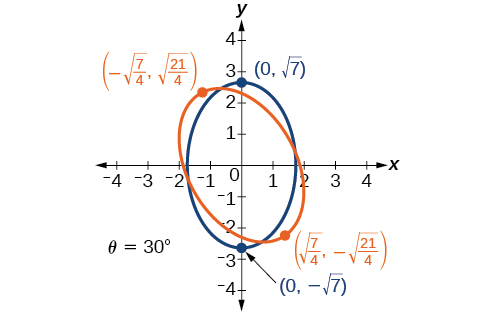
44)$11x^2+10\sqrt{3}xy+y^2-64=0$

45)$21x^2+2\sqrt{3}xy+19y^2-18=0$

Responder

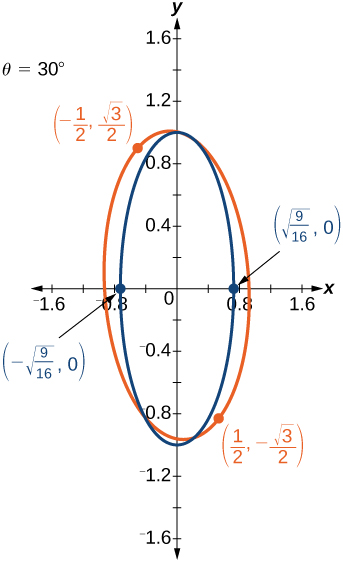
46)$16x^2+24xy+9y^2-130x+90y=0$

47)$16x^2+24xy+9y^2-60x+80y=0$

Responder

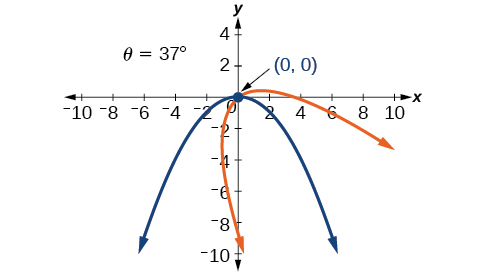
48)$13x^2-6\sqrt{3}xy+7y^2-16=0$

49)$4x^2-4xy+y^2-8\sqrt{5}x-16\sqrt{5}y=0$

Responder

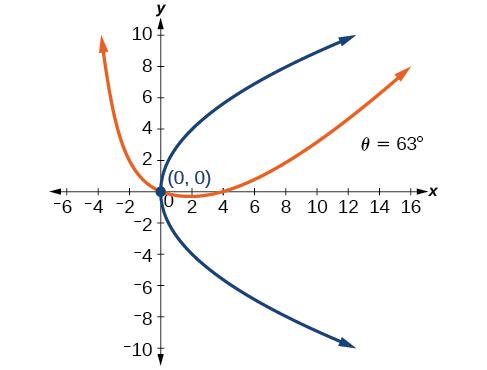
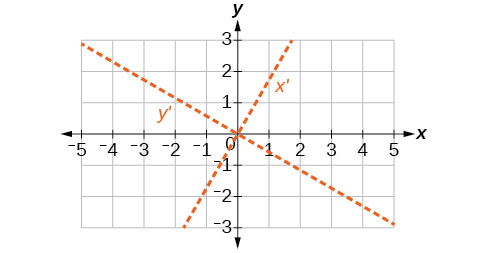
Para los ejercicios 50-55, determinar el ángulo de rotación con el fin de eliminar el$xy$ término. Después grafica el nuevo conjunto de ejes.

50)$6x^2-5\sqrt{3}xy+y^2+10x-12y=0$

51)$6x^2-5xy+6y^2+20x-y=0$

Responder

$\theta =45^{\circ}$

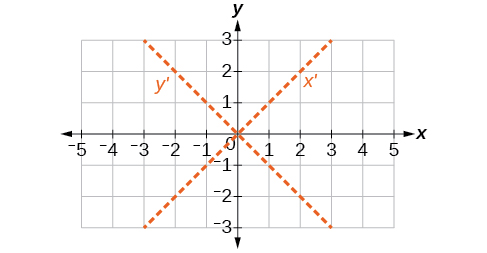
52)$6x^2-8\sqrt{3}xy+14y^2+10x-3y=0$

53)$4x^2+6\sqrt{3}xy+10y^2+20x-40y=0$

Responder

$\theta =60^{\circ}$

54)$8x^2+3xy+4y^2+2x-4=0$

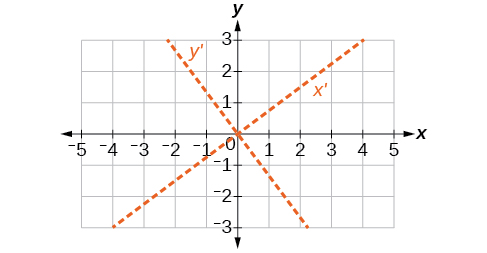
55)$16x^2+24xy+9y^2+20x-44y=0$

Responder

$\theta \approx 36.9^{\circ}$

Para los ejercicios 56-60, determinar el valor de con$k$ base en la ecuación dada.

56) Dado$4x^2+kxy+16y^2+8x+24y-48=0$, encuentra$k$ para que la gráfica sea una parábola.

57) Dado$2x^2+kxy+12y^2+10x-16y+28=0$, encuentra$k$ que la gráfica sea una elipse.

Responder

$-4\sqrt{6}<k<4\sqrt{6}$

58) Dado$3x^2+kxy+4y^2-6x+20y+128=0$, encuentra$k$ que la gráfica sea una hipérbola.

59) Dado$kx^2+8xy+8y^2-12x+16y+18=0$ hallazgo$k$ para que la gráfica sea una parábola.

Responder

$k=2$

60) Dado$6x^2+12xy+ky^2+16x+10y+4=0$ hallazgo$k$ para que la gráfica sea una elipse.

10.5: Secciones cónicas en coordenadas polares

En esta sección, aprenderemos a definir cualquier cónica en el sistema de coordenadas polares en términos de un punto fijo, el foco en el polo, y una línea, la directrix, que es perpendicular al eje polar.

Verbal

1) Explicar cómo la excentricidad determina qué sección cónica se da.

Responder

Si la excentricidad es menor que$1$, es una elipse. Si la excentricidad es igual a$1$, es una parábola. Si la excentricidad es mayor que$1$, es una hipérbola.

2) Si una sección cónica se escribe como una ecuación polar, ¿qué debe ser cierto del denominador?

3) Si una sección cónica se escribe como una ecuación polar, y el denominador implica$\sin \theta$ ¿qué conclusión se puede sacar sobre la directrix?

Responder

La directrix será paralela al eje polar.

4) Si la directriz de una sección cónica es perpendicular al eje polar, ¿qué sabemos de la ecuación de la gráfica?

5) ¿Qué sabemos del foco/focos de una sección cónica si se escribe como una ecuación polar?

Responder

Uno de los focos se ubicará en el origen.

Algebraico

Para los ejercicios 6-17, identificar la cónica con un foco en el origen, para luego dar la directriz y excentricidad.

6)$r=\dfrac{6}{1-2\cos \theta }$

7)$r=\dfrac{3}{4-4\sin \theta }$

Contestar

Parábola con$e=1$ y$\dfrac{3}{4}$ unidades directrix debajo del poste.

8)$r=\dfrac{8}{4-3\cos \theta }$

9)$r=\dfrac{5}{1+2\sin \theta }$

Contestar

Hipérbola con$e=2$ y$\dfrac{5}{2}$ unidades directrix por encima del polo.

10)$r=\dfrac{15}{4+3\cos \theta }$

11)$r=\dfrac{3}{10+10\cos \theta }$

Contestar

Parábola con$e=1$ y$\dfrac{3}{10}$ unidades directrix a la derecha del poste.

12)$r=\dfrac{2}{1-\cos \theta }$

13)$r=\dfrac{4}{7+2\cos \theta }$

Contestar

Elipse con$e=\dfrac{2}{7}$ y$2$ unidades directrix a la derecha del poste.

14)$r(1-\cos \theta )=3$

15)$r(3+5\sin \theta )=11$

Contestar

Hipérbola con$e=\dfrac{5}{3}$ y$\dfrac{11}{5}$ unidades directrix por encima del polo.

16)$r(4-5\sin \theta )=1$

17)$r(7+8\sin \theta )=7$

Contestar

Hipérbola con$e=\dfrac{8}{7}$ y$\dfrac{7}{8}$ unidades directrix a la derecha del poste.

Para los ejercicios 18-30, convertir la ecuación polar de una sección cónica en una ecuación rectangular.

18)$r=\dfrac{4}{1+3\sin \theta }$

19)$r=\dfrac{2}{5-3\sin \theta }$

Contestar

$25x^2+16y^2-12y-4=0$

20)$r=\dfrac{8}{3-2\cos \theta }$

21)$r=\dfrac{3}{2+5\cos \theta }$

Contestar

$21x^2-4y^2-30x+9=0$

22)$r=\dfrac{4}{2+2\sin \theta }$

23)$r=\dfrac{3}{8-8\cos \theta }$

Contestar

$64y^2=48x+9$

24)$r=\dfrac{2}{6+7\cos \theta }$

25)$r=\dfrac{5}{5-11\sin \theta }$

Contestar

$96y^2-25x^2+110y+25=0$

26)$r(5+2\cos \theta )=6$

27)$r(2-\cos \theta )=1$

Contestar

$3x^2+4y^2-2x-1=0$

28)$r(2.5-2.5\sin \theta )=5$

29)$r=\dfrac{6\sec \theta }{-2+3\sec \theta }$

Contestar

$5x^2+9y^2-24x-36=0$

30)$r=\dfrac{6\csc \theta }{3+2\csc \theta }$

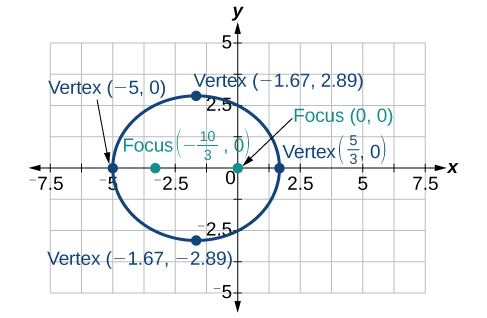
Para los ejercicios 31-42, grafica la sección cónica dada. Si es una parábola, etiquete el vértice, el enfoque y la directrix. Si es una elipse, etiquetar los vértices y focos. Si se trata de una hipérbola, etiquetar los vértices y focos.

31)$r=\dfrac{5}{2+\cos \theta }$

Contestar

32)$r=\dfrac{2}{3+3\sin \theta }$

33)$r=\dfrac{10}{5-4\sin \theta }$

Contestar

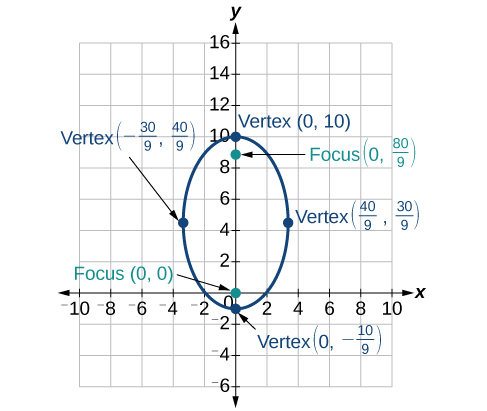
34)$r=\dfrac{3}{1+2\cos \theta }$

35)$r=\dfrac{8}{4-5\cos \theta }$

Contestar

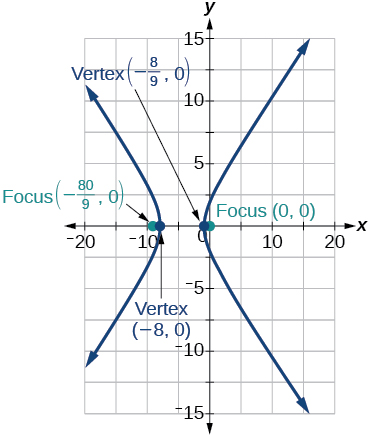
36)$r=\dfrac{3}{4-4\cos \theta }$

37)$r=\dfrac{2}{1-\sin \theta }$

Contestar

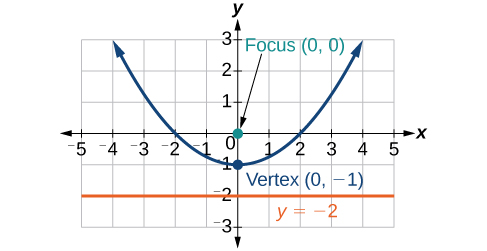
38)$r=\dfrac{6}{3+2\sin \theta }$

39)$r(1+\cos \theta )=5$

Contestar

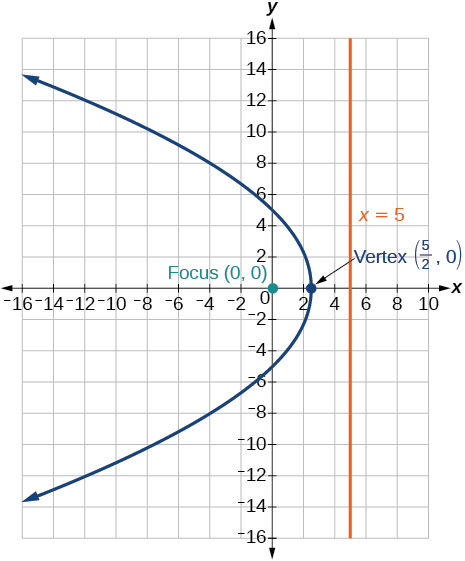
40)$r(3-4\sin \theta )=9$

41)$r(3-2\sin \theta )=6$

Contestar

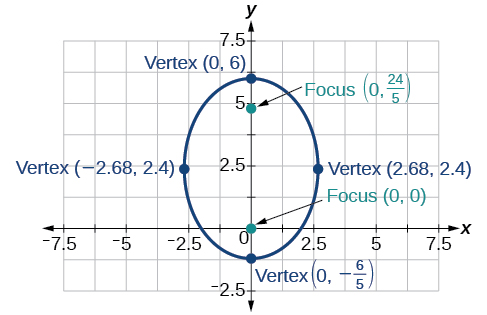
42)$r(4-6\cos \theta )=5$

Para los ejercicios 43-, encuentra la ecuación polar de la cónica con foco en el origen y la excentricidad y directriz dadas.

43) Directrix:$x=4$;$e=\dfrac{1}{5}$

Contestar

$r=\dfrac{4}{5+\cos \theta }$

44) Directrix:$x=-4$;$e=5$

45) Directrix:$y=2$;$e=2$

Contestar

$r=\dfrac{4}{1+2\sin \theta }$

46) Directrix:$y=-2$;$e=\dfrac{1}{2}$

47) Directrix:$x=1$;$e=1$

Contestar

$r=\dfrac{1}{1+\cos \theta }$

48) Directrix:$x=-1$;$e=1$

49) Directrix:$x=-\dfrac{1}{4}$;$e=\dfrac{7}{2}$

Contestar

$r=\dfrac{7}{8-28\cos \theta }$

50) Directrix:$y=-\dfrac{2}{5}$;$e=\dfrac{7}{2}$

51) Directrix:$y=4$;$e=\dfrac{3}{2}$

Contestar

$r=\dfrac{12}{2+3\sin \theta }$

52) Directrix:$x=-2$;$e=\dfrac{8}{3}$

53) Directrix:$x=-5$;$e=\dfrac{3}{4}$

Contestar

$r=\dfrac{15}{4-3\cos \theta }$

54) Directrix:$y=2$;$e=2.5$

55) Directrix:$x=-3$;$e=\dfrac{1}{3}$

Contestar

$r=\dfrac{3}{3-3\cos \theta }$

Extensiones

Recordemos de Rotación de Ejes que las ecuaciones de cónicas con un$xy$ término tienen gráficas rotadas. Para los siguientes ejercicios, expresar cada ecuación en forma polar con$r$ como una función de$\theta$.

56)$xy=2$

57)$x^2+xy+y^2=4$

Contestar

$r=\pm \dfrac{2}{\sqrt{1+\sin \theta \cos \theta }}$

58)$2x^2+4xy+2y^2=9$

59)$16x^2+24xy+9y^2=4$

Contestar

$r=\pm \dfrac{2}{4\cos \theta +3\sin \theta }$

60)$2xy+y=1$

Colaboradores y Atribuciones

• Template:OpenStaxPreCalc