10.R: Geometría Analítica (Revisión)

Última actualización
Guardar como PDF

Page ID: 121603

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

10.1: La elipse

En esta sección, investigaremos la forma de esta sala y sus aplicaciones en el mundo real, incluyendo hasta qué punto de distancia pueden pararse dos personas en Statuary Hall y aún escucharse susurrar entre sí.

Para los ejercicios 1-4, escriba la ecuación de la elipse en forma estándar. Luego identificar el centro, los vértices y los focos.

1)$\dfrac{x^2}{25}+\dfrac{y^2}{64}=1$

Contestar: $\dfrac{x^2}{5^2}+\dfrac{y^2}{8^2}=1$; centro:$(0,0)$; Vértices:$(5,0)$$(-5,0)$,$(0,8)$,,$(0,-8)$; focos:$(0,\sqrt{39})$,$(0,-\sqrt{39})$

2)$\dfrac{(x-2)^2}{100}+\dfrac{(y+3)^2}{36}=1$

3)$9x^2+y^2+54x-4y+76=0$

Contestar: $\dfrac{(x+3)^2}{1^2}+\dfrac{(y-2)^2}{3^2}=1$; centro:$(-3,2)$; Vértices:$(-2,2)$$(-4,2)$,$(-3,5)$,,$(-3,-1)$; focos:$(-3,2+2\sqrt{2})$,$(-3,2-2\sqrt{2})$

4)$9x^2+36y^2-36x+72y+36=0$

Para los ejercicios 5-8, grafica la elipse, señalando el centro, los vértices y los focos.

5)$\dfrac{x^2}{36}+\dfrac{y^2}{9}=1$

Contestar

centro:$(0,0)$; Vértices:$(6,0$$(-6,0)$,$(0,3)$,,$(0,-3)$; focos:$(3\sqrt{3},0)$,$(-3\sqrt{3},0)$

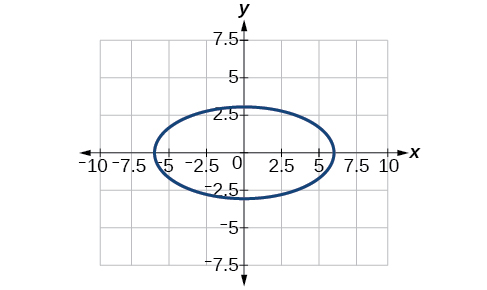
$R10.1.5.png$

6)$\dfrac{(x-4)^2}{25}+\dfrac{(y+3)^2}{49}=1$

7)$4x^2+y^2+16x+4y-44=0$

Contestar

centro:$(-2,-2)$; Vértices:$(2,-2)$$(-6,-2)$,$(-2,6)$,,$(-2,-10)$; focos:$(-2,-2+4\sqrt{3})$,$(-2,-2-4\sqrt{3})$

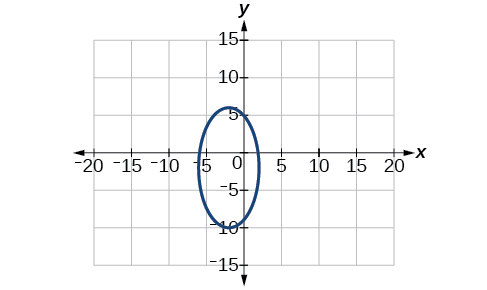
$R10.1.7.png$

8)$2x^2+3y^2-20x+12y+38=0$

Para los ejercicios 9-11, use la información dada para encontrar la ecuación para la elipse.

9) Centrar en$(0,0)$, enfocarse en$(3,0)$, vértice en$(-5,0)$

Contestar: $\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$

10) Centrar en$(2,-2)$, vértice en$(7,-2)$, enfoque en$(4,-2)$

11) Se va a construir una galería susurrante de tal manera que los focos se localicen a$35$ pies del centro. Si la longitud de la galería va a ser$100$ pies, ¿cuál debería ser la altura del techo?

Contestar: Aproximadamente$35.71$ pies

10.2: La hipérbola

En geometría analítica, una hipérbola es una sección cónica formada por la intersección de un cono circular recto con un plano en un ángulo tal que ambas mitades del cono se intersectan. Esta intersección produce dos curvas independientes y no delimitadas que son imágenes especulares entre sí.

Para los ejercicios 1-4, escriba la ecuación de la hipérbola en forma estándar. Entonces dale el centro, los vértices y los focos.

1)$\dfrac{x^2}{81}-\dfrac{y^2}{9}=1$

2)$\dfrac{(y+1)^2}{16}-\dfrac{(x-4)^2}{36}=1$

Contestar: $\dfrac{(y+1)^2}{4^2}-\dfrac{(x-4)^2}{6^2}=1$; centro:$(4,-1)$; Vértices:$(4,3)$,$(4,-5)$; focos:$(4,-1+2\sqrt{13})$,$(4,-1-2\sqrt{13})$

3)$9y^2-4x^2+54y-16x+29=0$

4)$3x^2-y^2-12x-6y-9=0$

Contestar: $\dfrac{(x-2)^2}{2^2}-\dfrac{(y+3)^2}{(2\sqrt{3})^2}=1$; centro:$(2,-3)$; Vértices:$(4,-3)$,$(0,-3)$; focos:$(6,-3)$,$(-2,-3)$

Para los ejercicios 5-8, grafica la hipérbola, etiquetando vértices y focos.

5)$\dfrac{x^2}{9}-\dfrac{y^2}{16}=1$

6)$\dfrac{(y-1)^2}{49}-\dfrac{(x+1)^2}{4}=1$

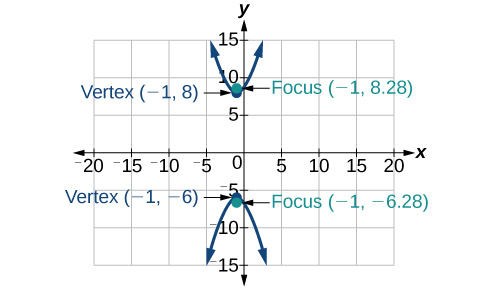
Contestar: $R10.2.6.png$

7)$x^2-4y^2+6x+32y-91=0$

8)$2y^2-x^2-12y-6=0$

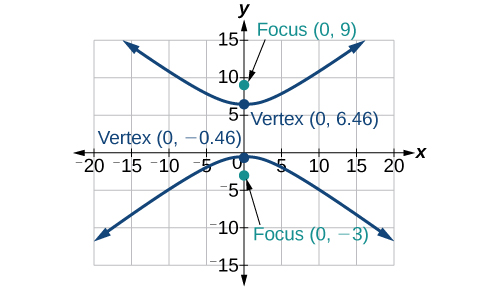
Contestar: $R10.2.8.png$

Para los ejercicios 9-10, encuentra la ecuación de la hipérbola.

9) Centro en$(0,0)$, vértice en$(0,4)$, enfoque en$(0,-6)$

10) Focos en$(3,7)$ y$(7,7)$, vértice en$(6,7$

Contestar: $\dfrac{(x-5)^2}{1}-\dfrac{(y-7)^2}{3}=1$

10.3: La Parábola

Al igual que la elipse y la hipérbola, la parábola también se puede definir por un conjunto de puntos en el plano de coordenadas. Una parábola es el conjunto de todos los puntos en un plano que están a la misma distancia de una línea fija, llamada directrix, y un punto fijo (el foco) no en la directrix.

Para los ejercicios 1-4, escriba la ecuación de la parábola en forma estándar. Luego dale el vértice, el enfoque y la directrix.

1)$y^2=12x$

2)$(x+2)^2=\dfrac{1}{2}(y-1)$

Contestar: $(x+2)^2=\dfrac{1}{2}(y-1)$; vértice:$(-2,1)$; foco:$ \left( -2, \dfrac{9}{8} \right ) $; directrix:$y=\dfrac{7}{8}$

3)$y^2-6y-6x-3=0$

4)$x^2+10x-y+23=0$

Contestar: $(x+5)^2=(y+2)$; vértice:$(-5,-2)$; foco:$ \left( -5, -\dfrac{7}{4} \right ) $; directrix:$y=-\dfrac{9}{4}$

Para los ejercicios 5-8, grafica la parábola, etiquetando vértice, enfoque y directrix.

5)$x^2+4y=0$

6)$(y-1)^2=\dfrac{1}{2}(x+3)$

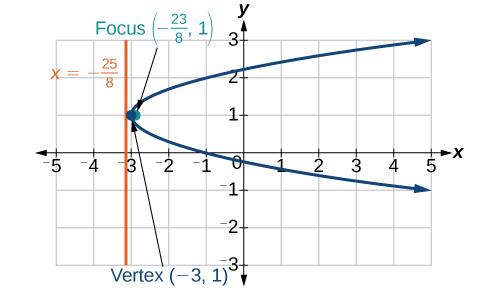
Contestar: $R10.3.6.png$

7)$x^2-8x-10y+46=0$

8)$2y^2+12y+6x+15=0$

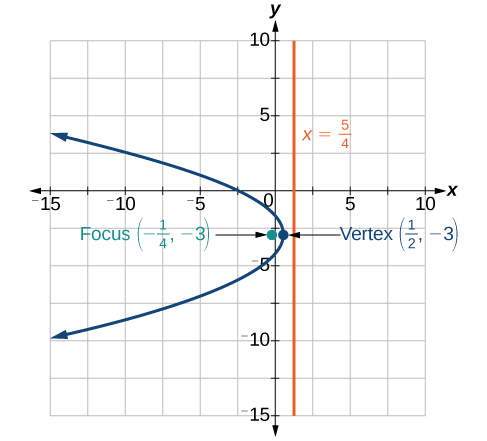
Contestar: $R10.3.8.png$

Para los ejercicios 9-11, escriba la ecuación de la parábola utilizando la información dada.

9) Enfoque en$(-4,0)$; directrix es$x=4$

10) Enfoque en$ \left( 2, \dfrac{9}{8} \right ) $; directrix es$y=\dfrac{7}{8}$

Contestar: $(x-2)^2= \left (\dfrac{1}{2} \right ) (y-1)$

11) Un plato receptor de TV por cable es la forma de un paraboloide de revolución. Encuentra la ubicación del receptor, que se coloca en el foco, si el plato tiene$5$ pies de ancho en su abertura y$1.5$ pies de profundidad.

10.4: Rotación de Ejes

En secciones anteriores de este capítulo, nos hemos centrado en las ecuaciones de forma estándar para secciones cónicas no degeneradas. En esta sección, desplazaremos nuestro enfoque hacia la ecuación de forma general, que puede ser utilizada para cualquier cónica. La forma general se establece igual a cero, y los términos y coeficientes se dan en un orden particular, como se muestra a continuación.

Para los ejercicios 1-3, determine cuál de las secciones cónicas está representada.

1)$16x^2+24xy+9y^2+24x-60y-60=0$

Contestar: $B^2 - 4AC =0$, parábola

2)$4x^2+14xy+5y^2+18x-6y+30=0$

3)$4x^2+xy+2y^2+8x-26y+9=0$

Contestar: $B^2 - 4AC = -31 < 0$, elipse

Para los ejercicios 4-5, determinar el ángulo$\theta $ que eliminará el$xy$ término, y escribir la ecuación correspondiente sin el$xy$ término.

4)$x^2+4xy-2y^2-6=0$

5)$x^2-xy+y^2-6=0$

Contestar: $\theta =45^{\circ},x'^2+3y'^2-12=0$

Para los ejercicios 6-8, grafica la ecuación relativa al$x'y'$ sistema en el que la ecuación no tiene$x'y'$ término.

6)$9x^2-24xy+16y^2-80x-60y+100=0$

7)$x^2-xy+y^2-2=0$

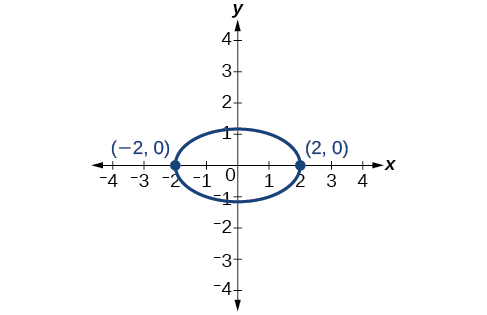
Contestar

$\theta =45^{\circ}$

$R10.4.7.png$

8)$6x^2+24xy-y^2-12x+26y+11=0$

10.5: Secciones cónicas en coordenadas polares

En esta sección, aprenderemos a definir cualquier cónica en el sistema de coordenadas polares en términos de un punto fijo, el foco en el polo, y una línea, la directrix, que es perpendicular al eje polar.

Para los ejercicios 1-4, dada la ecuación polar de la cónica con foco en el origen, identificar la excentricidad y directricidad.

1)$r=\dfrac{10}{1-5\cos \theta }$

Contestar: Hipérbola con$e=5$ y$2$ unidades directrix a la izquierda del poste.

2)$r=\dfrac{6}{3+2\cos \theta }$

3)$r=\dfrac{1}{4+3\sin \theta }$

Contestar: Elipse con$e=\dfrac{3}{4}$ y$\dfrac{1}{3}$ unidad directrix por encima del poste.

4)$r=\dfrac{3}{5-5\sin \theta }$

Para los ejercicios 5-8, grafica la cónica dada en forma polar. Si es una parábola, etiquete el vértice, el enfoque y la directrix. Si es una elipse o una hipérbola, etiquetar los vértices y focos.

5)$r=\dfrac{3}{1-\sin \theta }$

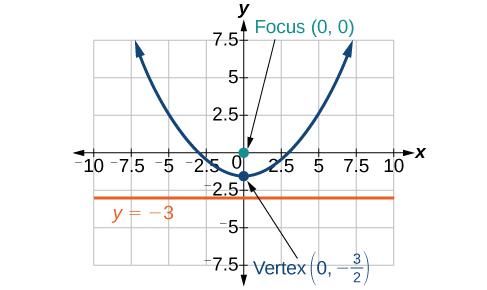
Contestar: $R10.5.5.png$

6)$r=\dfrac{8}{4+3\sin \theta }$

7)$r=\dfrac{10}{4+5\cos \theta }$

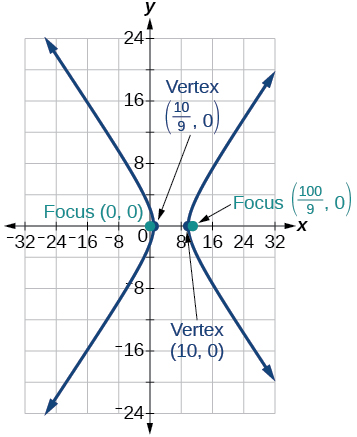
Contestar: $R10.5.7.png$

8)$r=\dfrac{9}{3-6\cos \theta }$

Para los ejercicios 9-10, dada la información sobre la gráfica de una cónica con foco en el origen, encuentra la ecuación en forma polar.

9) Directrix es$x=3$ y excentricidad$e=1$

Contestar: $r=\dfrac{3}{1+\cos \theta }$

10) Directrix es$y=-2$ y excentricidad$e=4$

Prueba de práctica

Para los ejercicios 1-2, escriba la ecuación en forma estándar y establezca el centro, los vértices y los focos.

1)$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$

Contestar: $\dfrac{x^2}{3^2}+\dfrac{y^2}{2^2}=1$; centro:$(0,0)$; vértices:$(3,0)$$(-3,0)$,$(0,2)$,,$(0,-2)$; focos:$(\sqrt{5},0)$,$(-\sqrt{5},0)$

2)$9y^2+16x^2-36y+32x-92=0$

Para los ejercicios 3-6, dibuje la gráfica, identificando el centro, los vértices y los focos.

3)$\dfrac{(x-3)^2}{64}+\dfrac{(y-2)^2}{36}=1$

Contestar

centro:$(3,2)$; vértices:$(11,2)$$(-5,2)$,$(3,8)$,,$(3,-4)$; focos:$(3+2\sqrt{7},2)$,$(3-2\sqrt{7},2)$

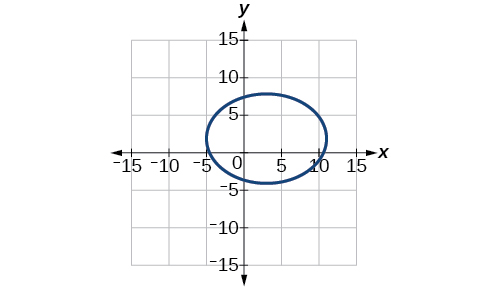
$RP3.png$

4)$2x^2+y^2+8x-6y-7=0$

5) Escribe la ecuación de forma estándar de una elipse con un centro en$(1,2)$, vértice en$(7,2)$, y enfoque en$(4,2)$.

Contestar: $\dfrac{(x-1)^2}{36}+\dfrac{(y-2)^2}{27}=1$

6) Una galería susurrante se construirá con una longitud de$150$ pies. Si los focos se van a ubicar a$20$ pies de distancia de la pared, ¿qué tan alto debe ser el techo?

Para los ejercicios 7-8, escriba la ecuación de la hipérbola en forma estándar, y dé el centro, vértices, focos y asíntotas.

7)$\dfrac{x^2}{49}-\dfrac{y^2}{81}=1$

Contestar: $\dfrac{x^2}{7^2}-\dfrac{y^2}{9^2}=1$; centro:$(0,0)$; vértices:$(7,0)$,$(-7,0)$; focos:$(\sqrt{130},0)$,$(-\sqrt{130},0)$; asíntotas:$y=\pm \dfrac{9}{7}x$

8)$16y^2-9x^2+128y+112=0$

Para los ejercicios 9-11, grafica la hipérbola, señalando su centro, vértices y focos. Indicar las ecuaciones de las asíntotas.

9)$\dfrac{(x-3)^2}{25}-\dfrac{(y+3)^2}{1}=1$

Contestar

centro:$(3,-3)$; vértices:$(8,-3)$,$(-2,-3)$; focos:$(3+\sqrt{26},-3)$,$(3-\sqrt{26},-3)$; asíntotas:$y=\pm \dfrac{1}{5}(x-3)-3$

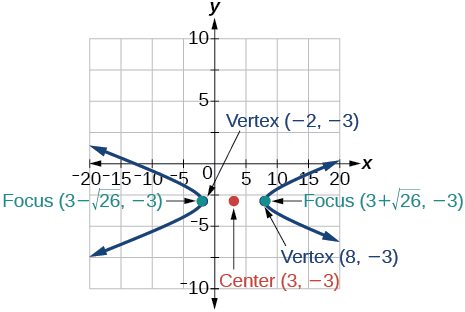
$RP9.png$

10)$y^2-x^2+4y-4x-18=0$

11) Escribir la ecuación de forma estándar de una hipérbola con focos en$(1,0)$, y$(1,6)$, y un vértice en$(1,2)$.

Contestar: $\dfrac{(y-3)^2}{1}-\dfrac{(x-1)^2}{8}=1$

Para los ejercicios 12-13, escriba la ecuación de la parábola en forma estándar, y dé el vértice, enfoque y ecuación de la directrix.

12)$y^2+10x=0$

13)$3x^2-12x-y+11=0$

Contestar: $(x-2)^2=\dfrac{1}{3}(y+1)$; vértice:$(2,-1)$; foco:$(2,-\dfrac{11}{12})$; directrix:$y=-\dfrac{13}{12}$

Para los ejercicios 14-17, grafica la parábola, etiquetando el vértice, el enfoque y la directrix.

14)$(x-1)^2=-4(y+3)$

15)$y^2+8x-8y+40=0$

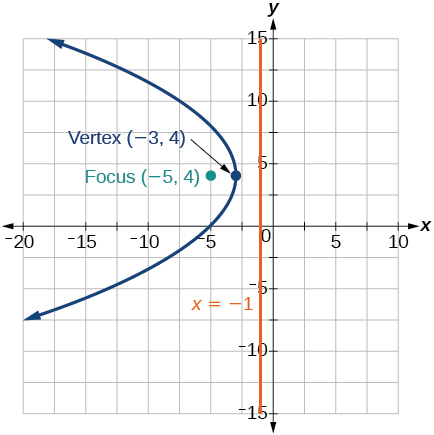
Contestar: $RP15.png$

16) Escribir la ecuación de una parábola con enfoque en$(2,3)$ y directrix$y=-1$.

17) Un foco de luz tiene la forma de un paraboloide de revolución. Si la fuente de luz se encuentra a$1.5$ pies de la base a lo largo del eje de simetría, y la profundidad del foco es$3$ pies, ¿cuál debería ser el ancho de la abertura?

Contestar: Aproximadamente$8.49$ pies

Para los ejercicios 18-19, determinar qué sección cónica está representada por la ecuación dada, y luego determinar el ángulo$\theta$ que eliminará el$xy$ término.

18)$3x^2-2xy+3y^2=4$

19)$x^2+4xy+4y^2+6x-8y=0$

Contestar: parábola;$\theta \approx 63.4^{\circ}$

Para los ejercicios 20-21, reescribir en el$x'y'$ sistema sin el$x'y'$ término, y graficar la gráfica rotada.

20)$11x^2+10\sqrt{3}xy+y^2=4$

21)$16x^2+24xy+9y^2-125x=0$

Contestar

$x'^2-4x'+3y'=0$

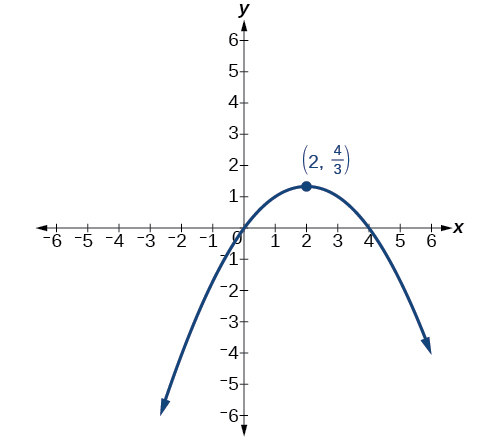
$RP21.png$

Para los ejercicios 22-23, identificar la cónica con foco en el origen, para luego dar la directriz y excentricidad.

22)$r=\dfrac{3}{2-\sin \theta }$

23)$r=\dfrac{5}{4+6\cos \theta }$

Contestar: Hipérbola con$e=\dfrac{3}{2}$ y$\dfrac{5}{6}$ unidades directrix a la derecha del poste.

Para los ejercicios 24-26, grafica la sección cónica dada. Si es una parábola, etiqueta vértice, enfoque y directrix. Si es una elipse o una hipérbola, etiquetar vértices y focos.

24)$r=\dfrac{12}{4-8\sin \theta }$

25)$r=\dfrac{2}{4+4\sin \theta }$

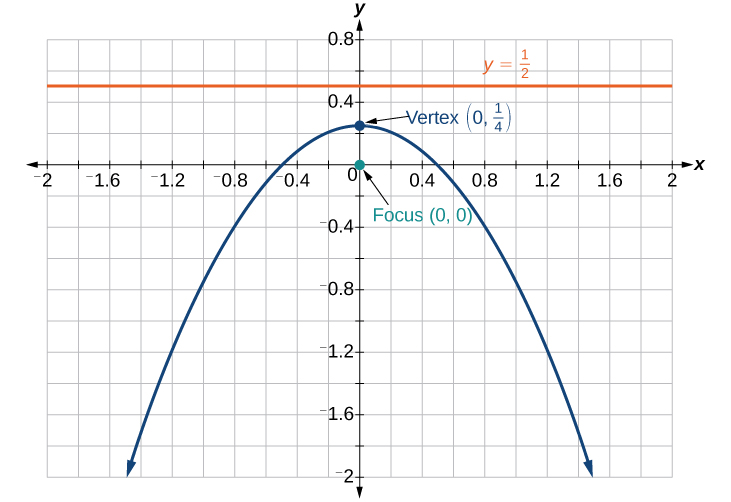
Contestar: $RP25.png$

26) Encontrar una ecuación polar de la cónica con foco en el origen, excentricidad de$e=2$, y directrix:$x=3$.

Colaboradores y Atribuciones

Template:OpenStaxPreCalc

Search

Text Color

Text Size

Margin Size

Font Type