12.4: Derivados
- Page ID
- 121512
El adolescente promedio en Estados Unidos abre la puerta de un refrigerador un estimado de 25 veces al día. Supuestamente, este promedio es superior a partir de hace 10 años cuando el adolescente promedio abrió la puerta de un refrigerador 20 veces al día 1. Se estima que una televisión está encendida en un hogar 6.75 horas diarias, mientras que los padres pasan aproximadamente 5.5 minutos diarios teniendo una conversación significativa con sus hijos. Estos promedios, también, no son los mismos que eran hace 10 años, cuando la televisión estaba en un estimado de 6 horas diarias en el hogar típico, y los padres pasaban 12 minutos diarios en conversación significativa con sus hijos. ¿Qué tienen en común estos escenarios? Las funciones que los representan han cambiado con el tiempo. En esta sección, consideraremos métodos para computar dichos cambios a lo largo del tiempo.
Encontrar la tasa promedio de cambio de una función
Las funciones que describen los ejemplos anteriores implican un cambio a lo largo del tiempo. El cambio dividido por el tiempo es un ejemplo de una tasa. Las tasas de cambio en los ejemplos anteriores son diferentes cada una. En otras palabras, algunos cambiaron más rápido que otros. Si tuviéramos que graficar las funciones, podríamos comparar las tasas determinando las pendientes de las gráficas.
Una línea tangente a una curva es una línea que cruza la curva en un solo punto pero no la cruza ahí. (La línea tangente puede intersectar la curva en otro punto alejado del punto de interés). Si ampliamos una curva en ese punto, la curva aparece lineal, y la pendiente de la curva en ese punto está cerca de la pendiente de la línea tangente en ese punto.
La figura\(\PageIndex{1}\) representa la función\(f(x)=x^3−4x\). Podemos ver la pendiente en varios puntos a lo largo de la curva.
- pendiente en\(x=−2\) es 8
- pendiente en\(x=−1\) es —1
- pendiente en\(x=2\) es 8
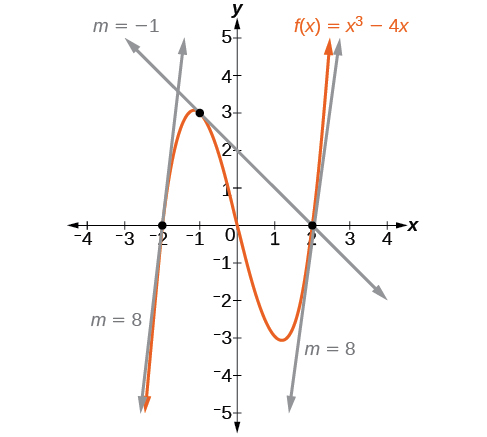
Imaginemos un punto en la curva de función\(f\) en\(x=a\) como se muestra en la Figura\(\PageIndex{1}\). Las coordenadas del punto son\((a,f(a))\). Conecte este punto con un segundo punto en la curva un poco a la derecha de\(x=a\), con un valor x incrementado en algún pequeño número real\(h\). Las coordenadas de este segundo punto son\((a+h,f(a+h))\) para algún valor positivo\(h\).
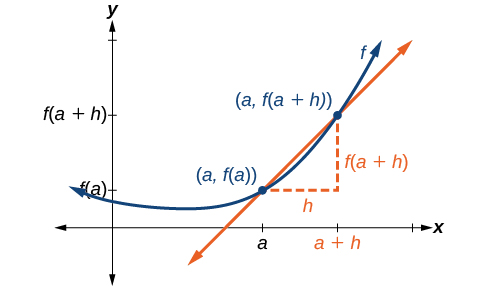
Podemos calcular la pendiente de la línea que conecta los dos puntos\((a,f(a))\) y\((a+h,f(a+h))\), llamada línea secante, aplicando la fórmula de pendiente,
\[ \mathrm{slope = \dfrac{change \; in \; y}{change \; in \; x}} \]
Utilizamos la notación\(m_{sec}\) para representar la pendiente de la línea secante que conecta dos puntos.
\[\begin{align} m_{sec} &= \dfrac{f(a+h)−f(a)}{(a+h)−(a) } \\ &= \dfrac{f(a+h)−f(a)}{\cancel{a}+h−\cancel{a}} \end{align}\]
La pendiente\(m_{sec}\) es igual a la tasa promedio de cambio entre dos puntos\((a,f(a))\) y\((a+h,f(a+h)).\)
\[m_{sec}=\dfrac{f(a+h)−f(a)}{h}\]
la TASA MEDIA DE CAMBIO ENTRE DOS PUNTOS EN UNA CURVA
La tasa promedio de cambio (AROC) entre dos puntos\((a,f(a))\) y\((a+h,f(a+h))\) en la curva de\(f\) es la pendiente de la línea que conecta los dos puntos y viene dada por
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Ejemplo\(\PageIndex{1}\): Finding the Average Rate of Change
Encuentra la tasa promedio de cambio conectando los puntos\((2,−6)\) y\((−1,5)\).
Solución
Sabemos que la tasa promedio de cambio que conecta dos puntos puede estar dada por
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}\]
Si un punto es\((2,−6)\), o\((2,f(2))\), entonces\(f(2)=−6.\)
El valor\(h\) es el desplazamiento de\(2\) a\(−1\), que es igual a\(−1−2=−3.\)
Para el otro punto,\(f(a+h)\) es la coordenada y at\(a+h\), que es más\(2+(−3)\) o\(−1,\) menos\(f(a+h)=f(−1)=5\).
\[\begin{align} \text{AROC} &= \dfrac{f(a+h)−f(a)}{h} \\ &=\dfrac{5−(−6)}{−3} \\&=\dfrac{11}{−3} \\ &=−\dfrac{11}{3} \end{align}\]
Ejercicio\(\PageIndex{1}\)
Encuentra la tasa promedio de cambio conectando los puntos\((−5,1.5)\) y\((−2.5,9)\)
Solución
3
Comprensión de la tasa instantánea de cambio
Ahora que podemos encontrar la tasa promedio de cambio, supongamos que hacemos\(h\) en Figura cada\(\PageIndex{2}\) vez más pequeña. Entonces\(a+h\) se acercará a\(a\) medida que\(h\) se hace más pequeño, cada vez más cerca de 0. De igual manera, el segundo punto\((a+h,f(a+h))\) se acercará al primer punto,\((a,f(a))\). Como consecuencia, la línea de conexión entre los dos puntos, llamada línea secante, se acercará cada vez más a ser una tangente a la función at\(x=a\), y la pendiente de la línea secante se acercará cada vez más a la pendiente de la tangente en\(x=a\) (Figura\(\PageIndex{3}\)).
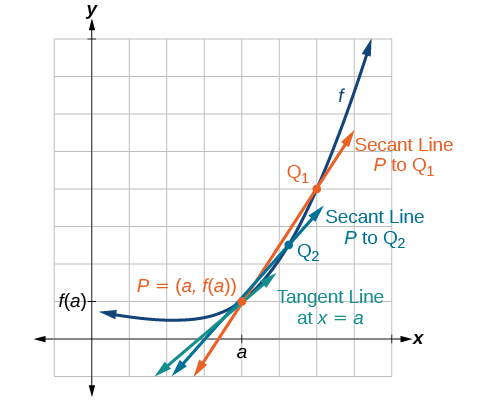
Debido a que estamos buscando la pendiente de la tangente en\(x=a\), podemos pensar en la medida de la pendiente de la curva de una función\(f\) en un punto dado como la tasa de cambio en un instante determinado. Llamamos a esta pendiente la tasa instantánea de cambio, o la derivada de la función en\(x=a.\) Ambos se puede encontrar encontrando el límite de la pendiente de una línea que conecta el punto en\(x=a\) con un segundo punto infinitesimalmente cercano a lo largo de la curva. Para una función\(f\) tanto la tasa instantánea de cambio de la función como la derivada de la función at\(x=a\) se escriben como\(f'(a),\) y podemos definirlos como un límite de dos lados que tiene el mismo valor ya sea abordado desde la izquierda o la derecha.
\[f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
La expresión por la que se encuentra el límite se conoce como cociente de diferencia.
DEFINICIÓN DE TASA DE CAMBIO INSTANTÁNEA
La derivada, o velocidad instantánea de cambio, de una función\(f\) at\(x=a\), viene dada por
\[ f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
La expresión\(\frac{f(a+h)−f(a)}{h}\) se llama cociente de diferencia.
Utilizamos el cociente de diferencia para evaluar el límite de la tasa de cambio de la función a medida que se\(h\) acerca a 0.
Derivadas: Interpretaciones y Notación
La derivada de una función puede ser interpretada de diferentes maneras. Se puede observar como el comportamiento de una gráfica de la función o calcularse como una tasa numérica de cambio de la función.
- La derivada de una función\(f(x)\) en un punto\(x=a\) es la pendiente de la línea tangente a la curva\(f(x)\) en\(x=a\). Se escribe la derivada\(x=a\) de\(f(x)\) at\(f′(a)\).
- La derivada\(f′(a)\) mide cómo cambia la curva en el punto\((a,f(a))\).
- La derivada\(f′(a)\) puede ser considerada como la velocidad instantánea de cambio de la función\(f(x)\) at\(x=a\).
- Si una función mide la distancia en función del tiempo, entonces la derivada mide la velocidad instantánea en el tiempo\(t=a\).
NOTACIONES PARA EL DERIVADO
La ecuación de la derivada de una función\(f(x)\) se escribe como\(y′=f′(x)\), donde\(y=f(x)\). La notación\(f′(x)\) se lee como “\(f\)primo de”\(x\). Las notaciones alternativas para la derivada incluyen las siguientes:
\[f′(x)=y′=\dfrac{dy}{dx}=\dfrac{df}{dx}=\dfrac{d}{dx} f(x)=Df(x)\]
La expresión\(f′(x)\) es ahora una función de\(x\); esta función da la pendiente de la curva\(y=f(x)\) a cualquier valor de\(x\). Se denota la derivada\(f(x)\) de una función en un punto\(x=a\)\(f′(a)\).
cómo: Dada una función\(f\), find the derivative by applying the definition of the derivative.
- Calcular\(f(a+h)\).
- Calcular\(f(a)\).
- Sustituir y simplificar\(\frac{f(a+h)−f(a)}{h}\).
- Evaluar el límite si existe:\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
Ejemplo\(\PageIndex{1}\): Finding the Derivative of a Polynomial Function
Encuentra la derivada de la función\(f(x)=x^2−3x+5\) en\(x=a.\)
Solución
Contamos con:
\[ f′(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \;\;\;\;\;\;\;\; \text{Definition of a derivative}\]
Sustituto\(f(a+h)=(a+h)^2−3(a+h)+5\) y\(f(a)=a^2−3a+5.\)
\[ \begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{(a+h)(a+h)−3(a+h)+5−(a^2−3a+5)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−3a−3h+5−a^2+3a−5}{h} && \text{Evaluate to remove parentheses.} \\ & = \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{3a}−3h+\cancel{5}−\cancel{a^2}+\cancel{3a}−\cancel{5}}{h} && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \dfrac{2ah+h^2−3h}{h} && \text{Factor out an }h. \\ & =2a+0−3 && \text{Evaluate the limit.} \\ &=2a−3 \end{align} \]
Ejercicio\(\PageIndex{1}\)
Encuentra la derivada de la función\(f(x)=3x^2+7x\) en\(x=a\)
Solución
\(f′(a)=6a+7\)
Encontrar Derivadas de Funciones Racionales
Para encontrar la derivada de una función racional, a veces simplificaremos la expresión utilizando técnicas algebraicas que ya hemos aprendido.
Ejemplo\(\PageIndex{1}\): Finding the Derivative of a Rational Function
Encuentra la derivada de la función\(f(x)=\dfrac{3+x}{2−x}\) en\(x=a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a})}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \\ &= \lim \limits_{h \to 0} \dfrac{(2−(a+h))(2−a)[ \frac{3+(a+h)}{2−(a+h)}−(\frac{3+a}{2−a}) ]}{(2−(a+h))(2−a)(h)} && \text{Multiply numerator and denominator by } (2−(a+h))(2−a) \\ & =\lim \limits_{h \to 0}\dfrac{(\cancel{2−(a+h)})(2−a)(\frac{3+(a+h)}{\cancel{(2−(a+h))}})−(2−(a+h))\cancel{(2−a)}(\frac{3+a}{\cancel{2−a}})}{(2−(a+h))(2−a)(h)} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{6−3a+2a−a^2+2h−ah−6+3a+3h−2a+a^2+ah}{(2−(a+h))(2−a)(h)} && \text{Multiply} \\ &=\lim \limits_{h \to 0} \dfrac{5 \cancel{h}}{(2−(a+h))(2−a)(\cancel{h})} && \text{Combine like terms} \\ & = \lim \limits_{h \to 0} \dfrac{5}{(2−(a+h))(2−a)} && \text{Cancel like factors} \\ & =\dfrac{5}{(2−(a+0))(2−a)}=\dfrac{5}{(2−a)(2−a)}=\dfrac{5}{(2−a)^2} && \text{Evaluate the limit} \end{align}\]
Ejercicio\(\PageIndex{1}\):
Encuentra la derivada de la función\(f(x)=\frac{10x+11}{5x+4}\) en\(x=a\).
\[f′(a)=\dfrac{−15}{(5a+4)^2}\]
Encontrar Derivadas de Funciones con Raíces
Para encontrar derivados de funciones con raíces, utilizamos los métodos que hemos aprendido para encontrar límites de funciones con raíces, incluyendo multiplicar por un conjugado.
Ejemplo\(\PageIndex{1}\): Finding the Derivative of a Function with a Root
Encuentra la derivada de la función\(f(x)=4\sqrt{x}\) en\(x=36.\)
Tenemos
\[\begin{align} f′(a) &=\lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} && \text{Substitute }f(a+h) \text{ and }f(a) \end{align}\]
Multiplicar el numerador y denominador por el conjugado:\(\frac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}}\).
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\bigg( \dfrac{4\sqrt{a+h}−4\sqrt{a}}{h} \bigg)⋅ \bigg(\dfrac{4\sqrt{a+h}+4\sqrt{a}}{4\sqrt{a+h}+4\sqrt{a}} \bigg) \\ &=\lim \limits_{h \to 0} \bigg( \dfrac{16(a+h)−16a}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Multiply.} \\ &=\lim \limits_{ h \to 0} \bigg( \dfrac{\cancel{16a}+16h\cancel{−16a}}{h4(\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Distribute and combine like terms.} \\ &= \lim \limits_{h \to 0}\bigg(\dfrac{16\cancel{h}}{\cancel{h}(4\sqrt{a+h}+4\sqrt{a})} \bigg) && \text{Simplify.} \\ & = \lim \limits_{h \to 0} \bigg( \dfrac{16}{4\sqrt{a+h}+4\sqrt{a}} \bigg) && \text{Evaluate the limit by letting } h=0. \\ & =\dfrac{16}{8\sqrt{a}}=\dfrac{2}{\sqrt{a}} \\ f′(36) &= \dfrac{2}{\sqrt{36}} && \text{Evaluate the derivative at } x=36. \\ &=\dfrac{2}{6} \\ & =\dfrac{1}{3} \end{align}\]
Ejercicio\(\PageIndex{1}\):
Encuentra la derivada de la función\(f(x)=9\sqrt{x}\) en\(x=9.\)
\(\frac{3}{2}\)
Encontrar tasas de cambio instantáneas
Muchas aplicaciones de la derivada implican determinar la tasa de cambio en un instante dado de una función con la variable tiempo independiente, razón por la cual se usa el término instantáneo. Considera la altura de una bola arrojada hacia arriba con una velocidad inicial de 64 pies por segundo, dada por\(s(t)=−16t^2+64t+6\), donde\(t\) se mide en segundos y\(s(t)\) se mide en pies. Sabemos que el camino es el de una parábola. El derivado nos dirá cómo está cambiando la altura en un momento dado. La altura de la bola se muestra en la Figura en función del tiempo. En física, llamamos a esto el “gráfico s - t”.
Ejemplo\(\PageIndex{1}\): Finding the Instantaneous Rate of Change
Usando la función anterior,\(s(t)=−16t^2+64t+6\), ¿cuál es la velocidad instantánea de la pelota a 1 segundo y 3 segundos en su vuelo?
La velocidad a\(t=1\) y\(t=3\) es la velocidad instantánea de cambio de distancia por tiempo, o velocidad. Observe que la altura inicial es de 6 pies. Para encontrar la velocidad instantánea, encontramos la derivada y la evaluamos a\(t=1\) y\(t=3\):
\[\begin{align} f′(a) &= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(t+h)^2+64(t+h)+6−(−16t^2+64t+6)}{h} && \text{Substitute } s(t+h) \text{ and } s(t). \\ &= \lim \limits_{h \to 0} \dfrac{−16t^2−32ht−h^2+64t+64h+6+16t^2−64t−6}{h} && \text{Distribute} \\ & =\lim \limits_{h \to 0} \dfrac{−32ht−h^2+64h}{h} && \text{Simplify.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(−32t−h+64)}{\cancel{h}} && \text{Factor the numerator.} \\ & =\lim \limits_{h \to 0}−32t−h+64 && \text{ Cancel out the common factor} h. \\ s′(t) &=−32t+64 && \text{Evaluate the limit by letting} h=0. \end{align}\]
Por cualquier valor de\(t\), nos\(s′(t)\) dice la velocidad a ese valor de\(t\).
Evaluar\(t=1\) y\(t=3\).
\[\begin{align}s′(1) &=−32(1)+64=32 \\ s′(3) &=−32(3)+64=−32 \end{align}\]
La velocidad de la bola después de 1 segundo es de 32 pies por segundo, ya que está en el camino hacia arriba.
La velocidad de la pelota después de 3 segundos es de −32 pies por segundo, ya que está en el camino hacia abajo.
Ejercicio\(\PageIndex{1}\):
La posición de la pelota viene dada por\(s(t)=−16t^2+64t+6.\) ¿Cuál es su velocidad 2 segundos en vuelo?
0
Uso de Gráficos para Encontrar Tasas de Cambio Instantáneas
Podemos estimar una tasa instantánea de cambio en\(x=a\) observando la pendiente de la curva de la función\(f(x)\) at\(x=a\). Esto lo hacemos dibujando una línea tangente a la función en\(x=a\) y encontrando su pendiente.
cómo: Dado un gráfico de una función\(f( x )\), find the instantaneous rate of change of the function at \(x=a\).
- Localizar\(x=a\) en la gráfica de la función\(f(x)\).
- Dibuja una línea tangente, una línea que atraviesa\(x=a\) en\(a\) y en ningún otro punto de esa sección de la curva. Extienda la línea lo suficiente como para calcular su pendiente como
\[\dfrac{\text{change in }y}{\text{change in }x.}\]
Ejemplo\(\PageIndex{1}\): Estimating the Derivative at a Point on the Graph of a Function
A partir de la gráfica de la función\(y=f(x)\) presentada en la Figura, estime cada una de las siguientes:
\(f(0) ; f(2) ; f'(0) ; f'(2)\)
Para encontrar el valor funcional,\(f(a)\), encontrar la coordenada y en\(x=a\).
Para encontrar la derivada en\(x=a, f′(a),\) dibujar una línea tangente en\(x=a,\) y estimar la pendiente de esa línea tangente. Ver Figura.
- \(f(0)\)es la coordenada y en\(x=0\). El punto tiene coordenadas\((0,1)\), así\(f(0)=1\).
- \(f(2)\)es la coordenada y en\(x=2\). El punto tiene coordenadas\((2,1)\), así\(f(2)=1\).
- \(f′(0)\)se encuentra estimando la pendiente de la línea tangente a la curva en\(x=0\). La línea tangente a la curva en\(x=0\) aparece horizontal. Las líneas horizontales tienen una pendiente de 0, así\(f′(0)=0\).
- \(f′(2)\)se encuentra estimando la pendiente de la línea tangente a la curva en\(x=2\). Observe la trayectoria de la línea tangente a la curva en\(x=2\). A medida que el\(x\) valor mueve una unidad hacia la derecha, el\(y\) valor sube cuatro unidades a otro punto de la línea. Así, la pendiente es de 4, entonces\(f′(2)=4\).
Ejercicio\(\PageIndex{1}\):
Utilizando la gráfica de la función\(f(x)=x^3−3x\) mostrada en la Figura, estimar:\(f(1), f′(1), f(0)\), y\(f′(0)\).
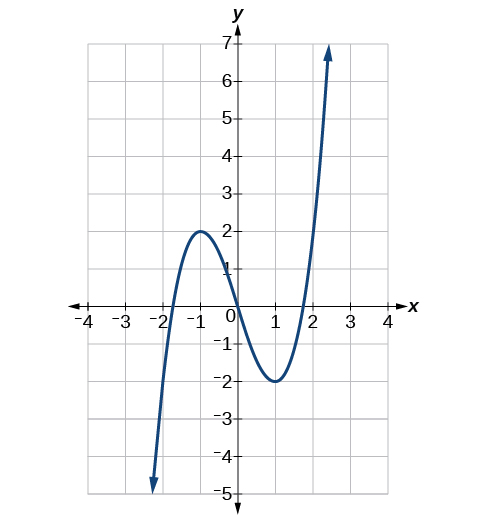
−2, −2,0, 0, −3
Uso de tasas de cambio instantáneas para resolver problemas del mundo real
Otra forma de interpretar una tasa instantánea de cambio en\(x=a\) es observar la función en un contexto del mundo real. La unidad para la derivada de una función\(f(x)\) es
\[\dfrac{\text{output units}}{\text{input unit}}\]
Tal unidad muestra por cuántas unidades cambia la salida por cada cambio de entrada de una unidad. La tasa instantánea de cambio en un instante dado muestra lo mismo: las unidades de cambio de salida por cambio de una unidad de entrada.
Un ejemplo de una tasa instantánea de cambio es un costo marginal. Por ejemplo, supongamos que el costo de producción para que una empresa produzca\(x\) artículos viene dado por\(C(x)\), en miles de dólares. La función derivada nos dice cómo está cambiando el costo para cualquier valor de\(x\) en el dominio de la función. Es decir,\(C′(x)\) se interpreta como un costo marginal, el costo adicional en miles de dólares de producir un artículo más cuando se han producido\(x\) artículos. Por ejemplo,\(C′(11)\) es el costo adicional aproximado en miles de dólares de producir el artículo 12 después de que se hayan producido 11 artículos. \(C′(11)=2.50\)significa que cuando se hayan producido 11 artículos, producir el 12 ° artículo aumentaría el costo total en aproximadamente $2,500.00.
Ejemplo\(\PageIndex{1}\): Finding a Marginal Cost
El costo en dólares de producir computadoras\(x\) portátiles en dólares es\(f(x)=x^2−100x.\) En el punto donde se han producido 200 computadoras, ¿cuál es el costo aproximado de producir la 201 st unidad?
Si\(f(x)=x^2−100x\) se describe el costo de producir\(x\) computadoras,\(f′(x)\) se describirá el costo marginal. Tenemos que encontrar el derivado. Para fines de calcular la derivada, podemos utilizar las siguientes funciones:
\[\begin{align} f(a+b) &=(x+h)^2−100(x+h) \\ f(a) &=a ^2−100a \end{align}\]
\[\begin{align} f′(x) &=\dfrac{f(a+h)−f(a)}{h} && \text{Formula for a derivative} \\ &=\dfrac{(x+h)^2−100(x+h)−(x^2−100x)}{h} \\ \text{Substitute }f(a+h) \text{ and }f(a). \\ & =\dfrac{x^2+2xh+h^2−100x−100h−x^2+100x}{h} && \text{Multiply polynomials, distribute.} \\ &= \text{2xh+h^2−100h}{h} && \text{Collect like terms.} \\ &=\dfrac{\cancel{h}(2x+h−100)}{\cancel{h}} && \text{Factor and cancel like terms.} \\ &=2x+h−100 && \text{Simplify.} \\ &=2x−100 && \text{Evaluate when }h=0. \\ f′(x) &=2x−100 && \text{Formula for marginal cost} \\ f′(200) &=2(200)−100=300 && \text{Evaluate for 200 units.} \end{align}\]
El costo marginal de producir la 201 st unidad será de aproximadamente $300.
Ejemplo\(\PageIndex{1}\):Interpreting a Derivative in Context
Un automóvil deja una intersección. La distancia que recorre en millas viene dada por la función\( f(t)\), donde\(t\) representa horas. Explique las siguientes anotaciones:
\(f(0)=0 f′(1)=60 f(1)=70 f(2.5)=150\)
Primero necesitamos evaluar la función\(f(t)\) y la derivada de la función\(f′(t)\), y distinguir entre las dos. Cuando evaluamos la función\(f(t)\), estamos encontrando la distancia que ha recorrido el automóvil en\(t\) horas. Cuando evaluamos la derivada f′ (t), f′ (t), estamos encontrando la velocidad del automóvil después de\(t\) horas.
- \(f(0)=0\)significa que en cero horas, el carro ha recorrido cero millas.
- \(f′(1)=60\)significa que una hora en el viaje, el automóvil está viajando 60 millas por hora.
- \(f(1)=70\)significa que a una hora del viaje, el carro ha recorrido 70 millas. En algún momento durante la primera hora, entonces, el automóvil debió haber viajado más rápido de lo que era en la marca de 1 hora.
- \(f(2.5)=150\)significa que a dos horas y treinta minutos del viaje, el automóvil ha recorrido 150 millas.
Ejercicio\(\PageIndex{1}\)
Un corredor corre por una carretera recta este-oeste. La función\(f(t)\) da cuántos pies hacia el este de su punto de partida se encuentra después de\(t\) segundos. Interpretar cada uno de los siguientes en lo que se refiere al corredor.
\(f(0)=0 ; f(10)=150 ; f′(10)=15 ; f′(20)=−10 ; f(40)=−100\)
- Después de cero segundos, ha viajado 0 pies.
- Después de 10 segundos, ha viajado 150 pies al este.
- Después de 10 segundos, se mueve hacia el este a una velocidad de 15 pies/seg.
- Después de 20 segundos, se mueve hacia el oeste a una velocidad de 10 pies/seg.
- Después de 40 segundos, se encuentra a 100 pies hacia el oeste de su punto de partida.
Encontrar puntos donde la derivada de una función no existe
Para entender dónde no existe la derivada de una función, necesitamos recordar lo que normalmente sucede cuando una función\(f(x)\) tiene una derivada en\(x=a\). Supongamos que usamos una utilidad gráfica para acercar el zoom\(x=a\). Si la función\(f(x)\) es diferenciable, es decir, si es una función que se puede diferenciar, entonces cuanto más cerca se acerca uno, más cerca se acerca la gráfica a una línea recta. Esta característica se llama linealidad.
Mira la gráfica en la Figura. Cuanto más acercamos el punto, más lineal aparecerá la curva.
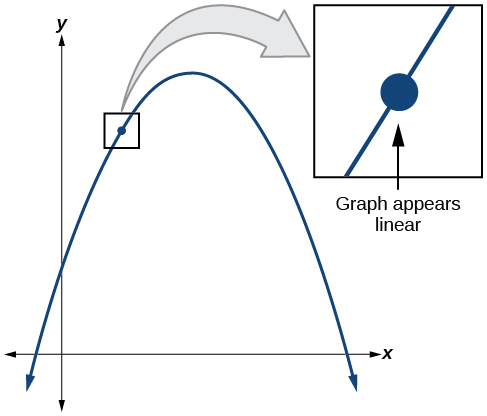
Gráfica de la función\(f(x)=| x |\), con eje x de —0.1 a 0.1 y eje y de —0.1 a 0.1.
¿Cuáles son las características de una gráfica que en un momento no es diferenciable? Aquí hay algunos ejemplos en los que la función no\(f(x)\) es diferenciable en\(x=a\).
En la Figura, vemos la gráfica de
\[f(x)=\begin{cases} x^2, &&x≤2 \\ 8−x, &&x>2.\end{cases} .\]
Observe que, a medida que\(x\) se acerca a 2 desde la izquierda, se puede observar que el límite de la izquierda es 4, mientras que a medida que se\(x\) acerca a 2 desde la derecha, se puede observar que el límite de la derecha es 6. Vemos que tiene una discontinuidad en\(x=2\).
La gráfica de\(f(x)\) tiene una discontinuidad en\(x=2\).
En Figura, vemos la gráfica de\(f(x)=|x|\). Vemos que la gráfica tiene un punto de esquina en\(x=0\).
La gráfica de\(f(x)=| x |\) tiene un punto de esquina en\(x=0\).
En la Figura, vemos que la gráfica de\(f(x)=x^{\frac{2}{3}}\) tiene una cúspide en\(x=0\). Una cúspide tiene una característica única. Alejándose de la cúspide, tanto los límites de la izquierda como de la derecha se acercan al infinito o al infinito negativo. Observe las líneas tangentes a medida que\(x\) se acerca a 0 tanto desde la izquierda como desde la derecha aparecen cada vez más pronunciadas, pero una tiene una pendiente negativa, la otra tiene una pendiente positiva.
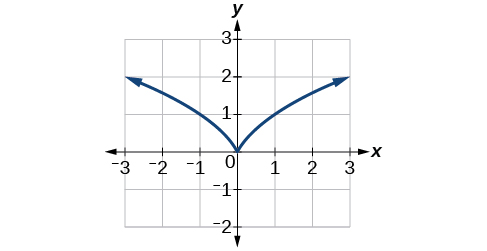
La gráfica de\(f(x)=x^\frac{2}{3}\) tiene una cúspide en\(x=0\).
En la Figura, vemos que la gráfica de\(f(x)=x^{frac{1}{3}}\) tiene una tangente vertical en\(x=0\). Recordemos que las tangentes verticales son líneas verticales, por lo que donde existe una tangente vertical, la pendiente de la línea es indefinida. Es por ello que la derivada, que mide la pendiente, no existe ahí.
La gráfica de\(f(x)=x^\frac{1}{3}\) tiene una tangente vertical en\(x=0\).
diferenciabilidad
Una función\(f(x)\) es diferenciable en\(x=a\) si la derivada existe at\(x=a\), lo que significa que\(f′(a)\) existe.
Hay cuatro casos para los que una función no\(f(x)\) es diferenciable en un momento dado\(x=a\).
- Cuando hay una discontinuidad en\(x=a\).
- Cuando hay un punto de esquina en\(x=a\).
- Cuando hay una cúspide en\(x=a\).
- Cualquier otro momento en el que haya una tangente vertical en\(x=a\).
Ejemplo\(\PageIndex{1}\): Determining Where a Function Is Continuous and Differentiable from a Graph
Usando Figura, determine dónde está la función
- continuo
- discontinuo
- diferenciable
- no diferenciable
En los puntos donde la gráfica es discontinua o no diferenciable, indicar por qué.
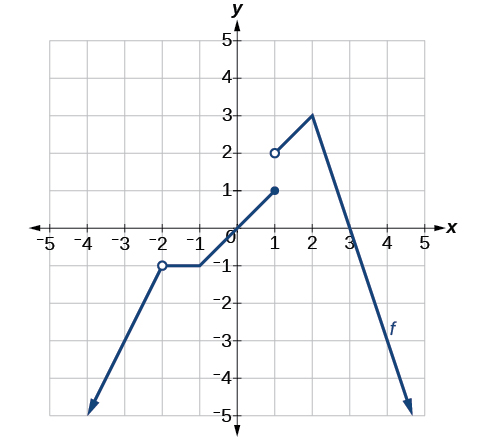
Tres intervalos donde la función es continua
La gráfica de es diferenciable en\((−∞,−2)∪(−2,−1)∪(−1,1)∪(1,2)∪(2,∞)\). El gráfico de no\(f(x)\) es diferenciable en\(x=−2\) porque es un punto de discontinuidad, en\(x=−1\) por una esquina afilada, en\(x=1\) porque es un punto de discontinuidad, y en\(x=2\) por una esquina afilada. Ver Figura.
Cinco intervalos donde la función es diferenciable
Ejercicio\(\PageIndex{1}\):
Determinar dónde la función\(y=f(x)\) mostrada en la Figura es continua y diferenciable de la gráfica.
La gráfica de\(f\) es continua en\((−∞,1)∪(1,3)∪(3,∞).\) La gráfica de f f es discontinua en\(x=1\) y\(x=3\). La gráfica de\(f\) es diferenciable en\((−∞,1)∪(1,3)∪(3,∞)\). La gráfica de no\(f\) es diferenciable en\(x=1\) y\(x=3\).
Encontrar una ecuación de una línea tangente a la gráfica de una función
La ecuación de una línea tangente a una curva de la función\(f(x)\) at\(x=a\) se deriva de la forma punto-pendiente de una línea,\(y=m(x−x_1)+y_1\). La pendiente de la línea es la pendiente de la curva en\(x=a\) y por lo tanto es igual a\(f′(a),\) la derivada de\(f(x)\) at\(x=a.\) El par de coordenadas del punto en la línea en\(x=a\) es\((a,f(a))\).
Si sustituimos en la forma punto-pendiente, tenemos
La ecuación de la línea tangente es
\[y=f'(a)(x−a)+f(a)\]
F
La ecuación de una línea tangente a la curva de una función\(f\) en un punto\(x=a\) es
\[y=f'(a)(x−a)+f(a)\]
cómo: Dada una función\(f\), find the equation of a line tangent to the function at \(x=a\).
- Encuentra la derivada de\(f(x)\) al\(x=a\) usar\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}.\)
- Evaluar la función en\(x=a\). Esto es\(f(a)\).
- Sustituto\((a,f(a))\) y\(f′(a)\) en\(y=f'(a)(x−a)+f(a)\).
- Escribe la ecuación de la línea tangente en el formulario\(y=mx+b\).
Ejemplo\(\PageIndex{1}\): Finding the Equation of a Line Tangent to a Function at a Point
Encuentra la ecuación de una línea tangente a la curva\(f(x)=x^2−4x\) en\(x=3.\)
Usando:
\[f'(a)= \lim \limits_{h \to 0} \dfrac{f(a+h)−f(a)}{h}\]
Sustituto\(f(a+h)=(a+h)^2−4(a+h)\) y\(f(a)=a^2−4a.\)
\[\begin{align} f′(a) &= \lim \limits_{h \to 0}\dfrac{(a+h)(a+h)−4(a+h)−(a2−4a)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{a^2+2ah+h^2−4a−4h−a^2+4a}{h} && \text{Remove parentheses.} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{a^2}+2ah+h^2−\cancel{4a}−4h−\cancel{a^2}+\cancel{4a}}{h} && \text{Combine like terms.} \\ &= \lim \limits_{h \to 0} \dfrac{2ah+h^2−4h}{h} \\ &= \lim \limits_{h \to 0} \dfrac{\cancel{h}(2a+h−4)}{h} && \text{Factor out }h. \\ &=2a+0−4 \\ f′(a)&=2a−4 && \text{Evaluate the limit.} \\ f′(3)&=2(3)−4=2 \end{align}\]
Ecuación de la línea tangente en\(x=3\):
\[\begin{align} y &= f'(a)(x−a)+f(a) \\ y &=f'(3)(x−3)+f(3) \\ y &=2(x−3)+(−3) \\ y &=2x−9 \end{align}\]
Análisis
Podemos usar una utilidad gráfica para graficar la función y la línea tangente. Al hacerlo, podemos observar el punto de tangencia en\(x=3\) como se muestra en la Figura.
Gráfica confirma el punto de tangencia en\(x=3\).
Ejercicio\(\PageIndex{1}\):
Encuentra la ecuación de una línea tangente a la curva de la función\(f(x)=5x^2−x+4\) en\(x=2\).
\(y=19x−16\)
Encontrar la velocidad instantánea de una partícula
Si una función mide la posición versus el tiempo, la derivada mide el desplazamiento versus el tiempo, o la velocidad del objeto. Un cambio en la velocidad o dirección en relación con un cambio en el tiempo se conoce como velocidad. La velocidad en un instante dado se conoce como velocidad instantánea.
Al tratar de encontrar la velocidad o velocidad de un objeto en un instante dado, parece que encontramos una contradicción. Normalmente definimos velocidad como la distancia recorrida dividida por el tiempo transcurrido. Pero en un instante, no se recorre distancia, y no transcurre el tiempo. ¿Cómo dividiremos cero por cero? El uso de un derivado resuelve este problema. Un derivado nos permite decir que aunque la velocidad del objeto cambia constantemente, tiene cierta velocidad en un instante dado. Eso significa que si el objeto viajara a esa velocidad exacta por una unidad de tiempo, recorrería la distancia especificada.
Velocidad instantánea
Deje que la\(s(t)\) función represente la posición de un objeto en\(t.\) el tiempo La velocidad instantánea o velocidad del objeto en el tiempo\(t=a\) viene dada por
\[s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h}\]
Ejemplo\(\PageIndex{1}\): Finding the Instantaneous Velocity
Una bola se lanza hacia arriba desde una altura de 200 pies con una velocidad inicial de 36 pies/seg. Si la altura de la pelota en pies después de\(t\) segundos se da por\(s(t)=−16t^2+36t+200,\) encontrar la velocidad instantánea de la pelota en\( t=2\).
Primero, debemos encontrar la derivada\(s′(t)\). Luego evaluamos la derivada en\(t=2\), usando\(s(a+h)=−16(a+h)^2+36(a+h)+200\) y\(s(a)=−16a^2+36a+200.\)
\[\begin{align} s′(a)= \lim \limits_{h \to 0} \dfrac{s(a+h)−s(a)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16(a+h)^2+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0} \dfrac{−16(a^2+2ah+h^2)+36(a+h)+200−(−16a^2+36a+200)}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−16a^2−32ah−16h^2+36a+36h+200+16a^2−36a−200}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{−16a^2}−32ah−16h^2+\cancel{36a}+36h+\cancel{200}+\cancel{16a^2}−\cancel{36a}−\cancel{200}}{h} \\ &= \lim \limits_{h \to 0}\dfrac{−32ah−16h^2+36h}{h} \\ &= \lim \limits_{h \to 0}\dfrac{\cancel{h}(−32a−16h+36)}{\cancel{h}} \\ &= \lim \limits_{h \to 0}(−32a−16h+36) \\&=−32a−16⋅0+36 \\ s′(a) &=−32a+36 \\ s′(2) &=−32(2)+36 \\ & =−28 \end{align}\]
Análisis
Este resultado significa que en el tiempo\(t=2\) segundos, la pelota está cayendo a una velocidad de 28 pies/seg.
Ejercicio\(\PageIndex{1}\):
Un cohete de fuegos artificiales es disparado hacia arriba desde un pozo a 12 pies bajo el suelo a una velocidad de 60 pies/seg. Su altura en pies después de\(t\) segundos viene dada por\(s=−16t^2+60t−12.\) ¿Cuál es su velocidad instantánea después de 4 segundos?
—68 pies/seg, está cayendo de nuevo a la Tierra a una velocidad de 68 pies/s.
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con derivados.
Visite este sitio web para obtener preguntas de práctica adicionales de Learningpod.
Ecuaciones Clave
| tasa promedio de cambio | \(\text{AROC}=\frac{f(a+h)−f(a)}{h}\) |
| derivada de una función | \(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\) |
Conceptos clave
- La pendiente de la línea secante que conecta dos puntos es la tasa promedio de cambio de la función entre esos puntos. Ver Ejemplo.
- La derivada, o tasa instantánea de cambio, es una medida de la pendiente de la curva de una función en un punto dado, o la pendiente de la línea tangente a la curva en ese punto. Ver Ejemplo, Ejemplo y Ejemplo.
- El cociente de diferencia es el cociente en la fórmula para la tasa instantánea de cambio:
\(\frac{f(a+h)−f(a)}{h}\)
- Las tasas de cambio instantáneas se pueden utilizar para encontrar soluciones a muchos problemas del mundo real. Ver Ejemplo.
- La tasa instantánea de cambio se puede encontrar observando la pendiente de una función en un punto de una gráfica dibujando una línea tangente a la función en ese punto. Ver Ejemplo.
- Las tasas de cambio instantáneas se pueden interpretar para describir situaciones del mundo real. Ver Ejemplo y Ejemplo.
- Algunas funciones no son diferenciables en un punto o puntos. Ver Ejemplo.
- La forma punto-pendiente de una línea se puede utilizar para encontrar la ecuación de una línea tangente a la curva de una función. Ver Ejemplo.
- La velocidad es un cambio de posición en relación con el tiempo. La velocidad instantánea describe la velocidad de un objeto en un instante dado. La velocidad promedio describe la velocidad mantenida durante un intervalo de tiempo.
- El uso de la derivada permite calcular la velocidad instantánea aunque no haya tiempo transcurrido. Ver Ejemplo.
Ejercicios de sección
Verbal
¿Cómo es similar la pendiente de una función lineal a la derivada?
La pendiente de una función lineal permanece igual. La derivada de una función general varía según\(x\). Tanto la pendiente de una línea como la derivada en un punto miden la tasa de cambio de la función.
¿Cuál es la diferencia entre la tasa promedio de cambio de una función en el intervalo\([ x,x+h ]\) y la derivada de la función at\(x\)?
Un automóvil viajó 110 millas durante el periodo de tiempo de 2:00 p.m. a 4:00 p.m. ¿Cuál fue la velocidad promedio del automóvil? Exactamente a las 2:30 P.M., la velocidad del automóvil registró exactamente 62 millas por hora. ¿Cuál es otro nombre para la velocidad del auto a las 2:30 P.M.? ¿Por qué esta velocidad difiere de la velocidad promedio?
La velocidad promedio es de 55 millas por hora. La velocidad instantánea a las 2:30 p.m. es de 62 millas por hora. La velocidad instantánea mide la velocidad del automóvil en un instante de tiempo, mientras que la velocidad promedio da la velocidad del automóvil a lo largo de un intervalo.
Explicar el concepto de la pendiente de una curva en punto\(x\).
Supongamos que el agua fluye hacia un tanque a una tasa promedio de 45 galones por minuto. Traducir este enunciado al lenguaje de las matemáticas.
La tasa promedio de cambio de la cantidad de agua en el tanque es de 45 galones por minuto. Si\(f(x)\) es la función que da la cantidad de agua en el tanque en cualquier momento\(t\), entonces la tasa promedio de cambio de\(f(x)\) entre\(t=a\) y\(t=b\) es\(f(a)+45(b−a).\)
Algebraico
Para los siguientes ejercicios, utilice la definición de derivada\(\lim \limits_{h to 0} \frac{f(x+h)−f(x)}{h}\) para calcular la derivada de cada función.
\(f(x)=3x−4\)
\(f(x)=−2x+1\)
\(f′(x)=−2\)
\(f(x)=x^2−2x+1\)
\ (f (x) = 2x^2+x−3
\(f′(x)=4x+1\)
\(f(x)=2x^2+5\)
\(f(x)=\frac{−1}{x−2}\)
\(f′(x)=\frac{1}{(x−2)^2}\)
\(f(x)=\frac{2+x}{1−x}\)
\(f(x)=\frac{5−2x}{3+2x}\)
\(\frac{−16(}{3+2x)^2}\)
\(f(x)=\sqrt{1+3x}\)
\(f(x)=3x^3−x^2+2x+5\)
\(f′(x)=9x^2−2x+2\)
\(f(x)=5\)
\(f(x)=5π\)
\(f′(x)=0\)
Para los siguientes ejercicios, encuentra la tasa promedio de cambio entre los dos puntos.
\((−2,0)\)y\((−4,5)\)
\((4,−3)\)y\((−2,−1)\)
\(−\frac{1}{3}\)
\((0,5)\)y\((6,5)\)
\((7,−2)\)y\((7,10)\)
undefined
Para las siguientes funciones polinómicas, encuentra las derivadas.
\(f(x)=x^3+1\)
\(f(x)=−3x^2−7x=6\)
\(f′(x)=−6x−7\)
\(f(x)=7x^2\)
\(f(x)=3x^3+2x^2+x−26\)
\(f′(x)=9x^2+4x+1\)
Para las siguientes funciones, encuentre la ecuación de la línea tangente a la curva en el punto\(x\) dado de la curva.
\(f(x)=2x^2−3x \;\;\; x=3\)
\(f(x)=x^3+1 \;\;\;\; x=2\)
\(y=12x−15\)
\(f(x)=\sqrt{x} \;\;\;\; x=9\)
Para el siguiente ejercicio, encuentra\(k\) tal que la línea dada sea tangente a la gráfica de la función.
\(f(x)=x^2−kx, \;\;\; y=4x−9\)
\(k=−10\)o\(k=2\)
Gráfica
Para los siguientes ejercicios, considere la gráfica de la función\(f\) y determine dónde la función es continua/discontinua y diferenciable/no diferenciable.
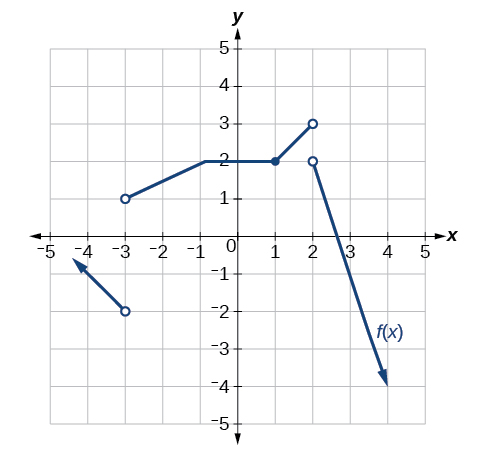
Discontinuo en\(x=−2\) y\(x=0\). No diferenciable a —2, 0, 2.
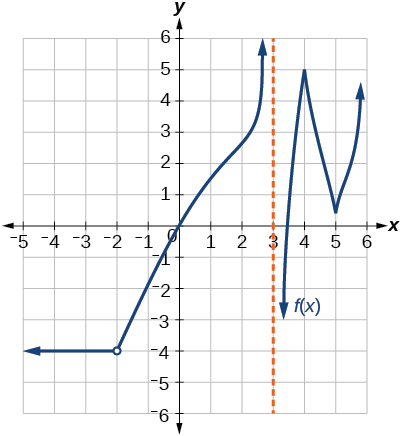
Discontinuo en\(x=5\). No diferenciable a -4, —2, 0, 1, 3, 4, 5.
Para los siguientes ejercicios, use Figura para estimar ya sea la función a un valor dado de\(x\) o la derivada a un valor dado de\(x\), como se indica.
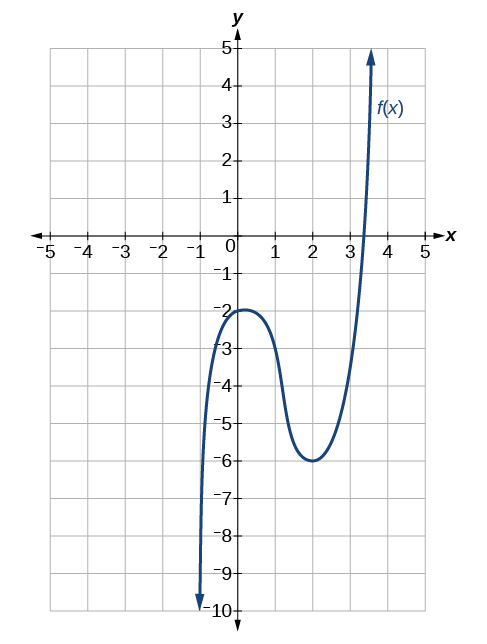
\(f(−1)\)
\(f(0)\)
\(f(0)=−2\)
\(f(1)\)
\(f(2)\)
\ (f (2) =−6f (2) =−6
\(f(3)\)
\(f′(−1)\)
\(f′(−1)=9\)
\(f′(0)\)
\(f′(1)\)
\(f′(1)=−3\)
\(f′(2)\)
\(f′(3)\)
\(f′(3)=9\)
Haga un boceto de la función en base a la siguiente información:
\(f′(x)=2x, f(2)=4\)
Tecnología
Evaluar numéricamente la derivada. Explore el comportamiento de la gráfica de\(f(x)=x^2\) alrededor\(x=1\) graficando la función en los siguientes dominios:\([ 0.9,1.1 ], [ 0.99,1.01 ], [ 0.999,1.001 ],\) y\([0.9999, 1.0001]\). Podemos usar la función en nuestra calculadora que configura automáticamente Ymin e Ymax a los valores Xmin y Xmax que preestablecemos. (En algunas de las calculadoras gráficas de uso común, esta característica puede llamarse ZOOM FIT o ZOOM AUTO). Al examinar los valores de rango correspondientes para esta ventana de visualización, aproximar cómo cambia la curva en es\(x=1,\) decir, aproximar la derivada en\(x=1.\)
Las respuestas varían. La pendiente de la línea tangente cercana\(x=1\) es 2.
Aplicaciones del mundo real
Para los siguientes ejercicios, explique la notación en palabras. El volumen\(f(t)\) de un tanque de gasolina, en galones,\(t\) minutos después del mediodía.
\(f(0)=600\)
\(f'(30)=−20\)
A las 12:30 p.m., la tasa de cambio del número de galones en el tanque es de —20 galones por minuto. Es decir, el tanque está perdiendo 20 galones por minuto.
\(f(30)=0\)
\(f'(200)=30\)
A los 200 minutos después del mediodía, el volumen de galones en el tanque está cambiando a razón de 30 galones por minuto.
\(f(240)=500\)
Para los siguientes ejercicios, explique las funciones en palabras. La altura,\(s\), de un proyectil después de\(t\) segundos viene dada por\(s(t)=−16t^2+80t.\)
\(s(2)=96\)
La altura del proyectil después de 2 segundos es de 96 pies.
\(s'(2)=16\)
\(s(3)=96\)
La altura del proyectil a los\(t=3\) segundos es de 96 pies.
\(s'(3)=−16\)
\(s(0)=0,s(5)=0.\)
La altura del proyectil es cero en\(t=0\) y otra vez en\(t=5\). Es decir, el proyectil inicia en el suelo y vuelve a caer a la tierra después de 5 segundos.
Para los siguientes ejercicios, el volumen\(V\) de una esfera con respecto a su radio\(r\) viene dado por\(V=\frac{4}{3}πr^3.\)
Encuentra la tasa promedio de cambio de\(V\) como\(r\) cambios de 1 cm a 2 cm.
Encuentra la tasa instantánea de cambio de\(V\) cuando r=3 cm. r=3 cm.
\(36π\)
Para los siguientes ejercicios, los ingresos generados por la venta de\(x\) artículos son dados por\(R(x)=2x^2+10x\).
Encuentre el cambio promedio de la función de ingresos como\(x\) cambios de\(x=10\) a\(x=20\).
Encontrar\(R'(10)\) e interpretar.
$50.00 por unidad, que es la tasa instantánea de cambio de ingresos cuando se venden exactamente 10 unidades.
Encontrar\(R'(15)\) e interpretar. Comparar\(R'(10),\) y\(R'(15)\) explicar la diferencia.
Para los siguientes ejercicios, el costo de producción de\(x\) celulares es descrito por la función\(C(x)=x^2−4x+1000.\)
Encuentre la tasa promedio de cambio en el costo total a medida que\(x\) cambia de\(x=10\) a\(x=15.\)
$21 por unidad
Encuentra el costo marginal aproximado, cuando se han producido 15 celulares, de producir el celular número 16.
Encuentra el costo marginal aproximado, cuando se han producido 20 celulares, de producir el celular número 21.
$36
Extensión
Para los siguientes ejercicios, utilice la definición para la derivada en un punto\(x=a\),\(\lim \limits_{x \to a}\frac{f(x)−f(a)}{x−a},\) para encontrar la derivada de las funciones.
\(f(x)=\frac{1}{x^2}\)
\(f(x)=5x^2−x+4\)
\(f'(x)=10a−1\)
\(f(x)=−x^2+4x+7\)
\(f(x)=\frac{−4}{3−x^2}\)
\(\frac{4}{(3−x)^2}\)
Ejercicios de revisión de capítulos
Encontrar límites: una aproximación numérica y gráfica
Para los siguientes ejercicios, use Figura.
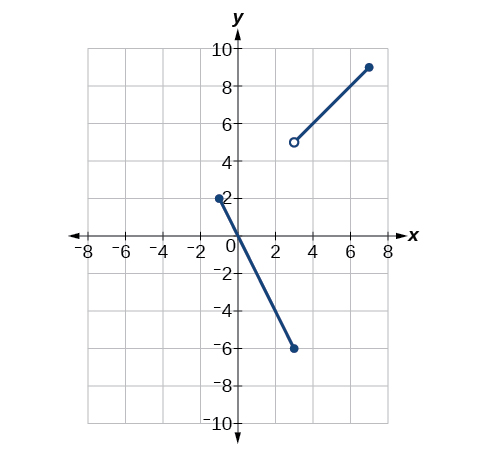
\(\lim \limits_{x \to −1^+}f(x)\)
2
\(\lim \limits_{x \to −1^−}f(x)\)
\(\lim \limits_{x \to −1} f(x)\)
no existe
\(\lim \limits_{x \to 3}f(x)\)
¿A qué valores de la función\(x\) es discontinua? ¿Qué condición de continuidad se viola?
Discontinuo en\(x=−1\) (\(\lim \limits_{x \to a} f(x)\)no existe),\(x=3\) (discontinuidad de salto), y\(x=7\) ((\ lim\ limits_ {x\ a} f (x)\) no existe).
Usando Tabla, estimación\(\lim \limits_{x \to 0}f(x).\)
| \(x\) | \(F(x)\) |
| −0.1 | 2.875 |
| −0.01 | 2.92 |
| −0.001 | 2.998 |
| 0 | Sin definir |
| 0.001 | 2.9987 |
| 0.01 | 2.865 |
| 0.1 | 2.78145 |
| 0.15 | 2.678 |
3
Para los siguientes ejercicios, con el uso de una utilidad gráfica, utilizar evidencia numérica o gráfica para determinar los límites izquierdo y derecho de la función dada como\(x\) enfoques\(a\). Si la función tiene límite a medida que\(x\) se aproxima\(a\), indicarlo. Si no, discuta por qué no hay límite.
\(f(x)=\begin{cases} | x |−1, && \text{if }x≠1 \\ x^3, \text{if }x=1 \end{cases} a=1\)
\(f(x)=\begin{cases} \frac{1}{x+1}, && \text{if }x=−2 \\ (x+1)^2, && \text{if }x≠−2 \end{cases} a=−2\)
\(\lim \limits_{x \to −2} f(x)=1\)
\(f(x)= \begin{cases} \sqrt{x+3} && \text{if } x < 1 \\ −\sqrt[3]{x} && \text{if }x>1 \end{cases} a=1\)
Encontrar límites: Propiedades de los límites
Para los siguientes ejercicios, encuentra los límites si\(\lim \limits_{x \to c} f(x)=−3\) y\(\lim \limits_{x \to c} g(x)=5\).
\(\lim \limits_{x \to c} (f(x)+g(x))\)
2
\(\lim \limits_{x \to c} \frac{f(x)}{g(x)}\)
\(\lim \limits_{x to c}(f(x)⋅g(x))\)
\(−15\)
\(\lim \limits_{x \to 0^+}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
\(\lim \limits_{x \to 0^-}f(x),f(x)= \begin{cases} 3x^2+2x+1 && x>0 \\ 5x+3 && x<0 \end{cases}\)
3
\(\lim \limits_{x \to 3^+}(3x−〚x〛)\)
Para los siguientes ejercicios, evaluar los límites utilizando técnicas algebraicas.
\(\lim \limits_{h \to 0}(\frac{(h+6)^2−36}{h})\)
12
\(\lim \limits_{x \to 25}(\frac{x^2−625}{\sqrt{x}−5)}\)
\(\lim \limits_{x \to 1}(\frac{−x^2−9x}{x})\)
−10
\(\lim \limits_{x \to 4}\frac{7−\sqrt{12x+1}}{x−4}\)
\(\lim \limits_{x \to −3}(\frac{\frac{1}{3}+\frac{1}{x}}{3+x})\)
\(−\frac{1}{9}\)
Continuidad
Para los siguientes ejercicios, use evidencia numérica para determinar si el límite existe en\(x=a\). Si no es así, describa el comportamiento de la gráfica de la función en\(x=a\).
\(f(x)=\frac{−2}{x−4}; a=4\)
\(f(x)=\frac{−2}{(x−4)^2}; a=4\)
At\(x=4\), la función tiene una asíntota vertical.
\(f(x)=\frac{−x}{x^2−x−6}; a=3\)
\(f(x)=\frac{6x^2+23x+20}{4x^2−25}; a=−\frac{5}{2}\)
discontinuidad removible en\(a=−\frac{5}{2}\)
\(f(x)=\frac{\sqrt{x}−3}{9−x}; a=9\)
Para los siguientes ejercicios, determine dónde\(f(x)\) es continua la función dada. Donde no sea continuo, indique qué condiciones fallan, y clasifique las discontinuidades.
\(f(x)=x^2−2x−15\)
continuo en\((−∞,∞)\)
\(f(x)=\frac{x^2−2x−15}{x−5}\)
\(f(x)=\frac{x^2−2x}{x^2−4x+4}\)
discontinuidad removible en no\(x=2. f(2)\) está definida, pero existen límites.
\(f(x)=\frac{x^3−125}{2x^2−12x+10}\)
\(f(x)=\frac{x^2−\frac{1}{x}}{2−x}\)
discontinuidad en\(x=0\) y\(x=2\). Ambos\(f(0)\) y no\(f(2)\) están definidos.
\(f(x)=\frac{x+2}{x^2−3x−10}\)
\(f(x)=\frac{x+2}{x^3+8}\)
discontinuidad removible en no\(x=–2. f(–2)\) está definida.
Derivados
Para los siguientes ejercicios, encuentra la tasa promedio de cambio\(\frac{f(x+h)−f(x)}{h}\).
\(f(x)=3x+2\)
\(f(x)=5\)
0
\(f(x)=\frac{1}{x+1}\)
\(f(x)= \ln (x)\)
\(\frac{\ln (x+h)− \ln (x)}{h}\)
\(f(x)=e^{2x}\)
Para los siguientes ejercicios, encuentra la derivada de la función.
\(f(x)=4x−6\)
\(=4\)
\(f(x)=5x^2−3x\)
Encuentra la ecuación de la línea tangente a la gráfica de\(f(x)\) al\(x\) valor indicado.
\(f(x)=−x^3+4x; x=2.\)
\(y=−8x+16\)
Para los siguientes ejercicios, con la ayuda de una utilidad gráfica, explicar por qué la función no es diferenciable en todas partes en su dominio. Especificar los puntos donde la función no es diferenciable.
\(f(x)=\frac{x}{| x |}\)
Dado que el volumen de un cono circular derecho es\(V=\frac{1}{3}πr^2h\) y que un cono dado tiene una altura fija de 9 cm y longitud de radio variable, encuentre la tasa instantánea de cambio de volumen con respecto a la longitud del radio cuando el radio sea de 2 cm. Dar una respuesta exacta en términos de\(π\)
\(12π\)
Prueba de práctica
Para los siguientes ejercicios, utilice la gráfica de\(f\) en la Figura.
\(f(1)\)
3
\(\lim \limits_{x \to −1^+}f(x)\)
\(\lim \limits_{x \to −1^-}f(x)\)
0
\(\lim \limits_{x \to −1}f(x)\)
\(\lim \limits_{x \to −2}f(x)\)
\(−1\)
¿A qué valores de\(x\) es\(f\) discontinuo? ¿Qué propiedad de continuidad se viola?
Para los siguientes ejercicios, con el uso de una utilidad gráfica, utilizar evidencia numérica o gráfica para determinar los límites izquierdo y derecho de la función dada como\(x\) enfoques\(a\). Si la función tiene un límite a medida que se\(x\) aproxima\(a\), indíquelo. Si no, discuta por qué no hay límite
\(f(x)=\begin{cases} \frac{1}{x}−3, && \text{if }x≤2 \\ x^3+1, && \text{if } x>2 \end{cases} a=2\)
\(\lim \limits_{x \to 2^−} f(x)=−\frac{5}{2}a\)y\(\lim \limits_{x \to 2^+} f(x)=9\) Así, el límite de la función como\(x\) se acerca a 2 no existe.
\(f(x)=\begin{cases} x^3+1, && \text{if }x<1 \\ 3x^2−1, && \text{if } x=1 \\ −\sqrt{x+3}+4, && \text{if } x>1 \end{cases} a=1\)
Para los siguientes ejercicios, evaluar cada límite utilizando técnicas algebraicas.
\(\lim \limits_{x \to −5}(\frac{\frac{1}{5}+\frac{1}{x}}{10+2x})\)
\(−\frac{1}{50}\)
\(\lim \limits_{h \to 0} (\frac{\sqrt{h^2+25}−5}{h^2})\)
\(\lim \limits_{h \to 0} (\frac{1}{h}−\frac{1}{h^2+h})\)
1
Para los siguientes ejercicios, determinar si la función dada\(f\) es continua o no. Si es continuo, muestra por qué. Si no es continuo, indique qué condiciones fallan.
\(f(x)=\sqrt{x^2−4}\)
\(f(x)=\frac{x^3−4x^2−9x+36}{x^3−3x^2+2x−6}\)
discontinuidad removible en\(x=3\)
Para los siguientes ejercicios, utilice la definición de una derivada para encontrar la derivada de la función dada en\(x=a\).
\(f(x)=\frac{3}{5+2x}\)
\(f(x)=\frac{3}{\sqrt{x}}\)
\(f'(x)=−\frac{3}{2a^{\frac{3}{2}}}\)
\(f(x)=2x^2+9x\)
discontinuo a —2,0, no diferenciable a —2,0, 2.
Para los siguientes ejercicios, con la ayuda de una utilidad gráfica, explicar por qué la función no es diferenciable en todas partes en su dominio. Especificar los puntos donde la función no es diferenciable.
\(f(x)=| x−2 |−| x+2 |\)
\(f(x)=\frac{2}{1+e^{\frac{2}{x}}}\)
no diferenciable en\(x=0\) (sin límite)
Para los siguientes ejercicios, explicar la notación en palabras cuando la altura de un proyectil en pies,\(s\), es una función del tiempo t t en segundos después del lanzamiento y viene dada por la función\(s(t)\).
\(s(0)\)
\(s(2)\)
la altura del proyectil en\(t=2\) segundos
\(s'(2)\)
\(\frac{s(2)−s(1)}{2−1}\)
la velocidad promedio de\(t=1\) a\(t=2\)
\(s(t)=0\)
Para los siguientes ejercicios, utilice la tecnología para evaluar el límite.
\(\lim \limits_{x \to 0} \frac{\sin (x)}{3x}\)
\(\frac{1}{3}\)
\(\lim \limits_{x \to 0} \frac{\tan ^2 (x)}{2x}\)
\(\lim \limits_{x \to 0}\frac{\sin (x)(1−\cos (x))}{2x^2}\)
0
Evaluar el límite a mano.
\(\lim \limits_{x \to 1}f(x), \text{where } f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
¿A qué valor (s) de\(x\) es discontinua la función por debajo?
\(f(x)= \begin{cases} 4x−7 && x≠1 \\ x^2−4 &&x=1 \end{cases}\)
Para los siguientes ejercicios, considere la función cuya gráfica aparece en la Figura.
Encuentra la tasa promedio de cambio de la función de\(x=1\) a\(x=3\).
2
Encuentra todos los valores de\(x\) en los que\(f'(x)=0\).
\(x=1\)
Encuentra todos los valores de\(x\) a los que\(f'(x)\) no existe.
Encuentra una ecuación de la línea tangente a la gráfica\(f\) del punto indicado:\(f(x)=3x^2−2x−6, x=−2\)
\(y=−14x−18\)
Para los siguientes ejercicios, utilice la función\(f(x)=x(1−x)^{\frac{2}{5}}\).
Grafica la función\(f(x)=x(1−x)^{\frac{2}{5}}\) ingresando\(f(x)=x((1−x)^2)^{\frac{1}{5}}\) y luego ingresando\(f(x)=x((1−x)^{\frac{1}{5}})^2\).
Explore el comportamiento de la gráfica de\(f(x)\) alrededor\(x=1\) graficando la función en los siguientes dominios, [0.9, 1.1], [0.99, 1.01], [0.999, 1.001], y [0.9999, 1.0001]. Utilice esta información para determinar si la función parece ser diferenciable en\(x=1\).
La gráfica no es diferenciable en\(x=1\) (cúspide).
Para los siguientes ejercicios, encuentra la derivada de cada una de las funciones usando la definición:\(\lim \limits_{h \to 0} \frac{f(x+h)−f(x)}{h}\)
\(f(x)=2x−8\)
\(f(x)=4x^2−7\)
\(f′(x)=8x\)
\(f(x)=x−\frac{1}{2}x^2\)
\(f(x)=\frac{1}{x+2}\)
\(f'(x)=−\frac{1}{(2+x)^2}\)
\(f(x)=\frac{3}{x−1}\)
\(f(x)=−x^3+1\)
\(f′(x)=−3^x2\)
\(f(x)=x^2+x^3\)
\(f(x)=\sqrt{x−1}\)
\(f'(x)=\frac{1}{2\sqrt{x−1}}\)
Notas al pie
- 1 www.csun.edu/ciencia/salud/d... tv&health.html Fuente proporcionada.
Glosario
- tasa promedio de cambio
- la pendiente de la línea que conecta los dos puntos\((a,f(a))\) y\((a+h,f(a+h))\) en la curva de\(f(x)\); viene dada por
\[\text{AROC}=\dfrac{f(a+h)−f(a)}{h}.\]
- derivado
- la pendiente de una función en un punto dado; denotada\(f′(a)\), en un punto\(x=a\) que es\(f′(a)=\lim \limits_{h \to 0}\frac{f(a+h)−f(a)}{h}\), siempre que exista el límite.
- diferenciable
- una función\(f(x)\) para la cual existe la derivada en\(x=a.\) En otras palabras, si existe f′ (a) f′ (a).
- tasa instantánea de cambio
- la pendiente de una función en un punto dado; en\(x=a\) ella viene dada por\(f′(a)=\lim \limits_{h \to 0} \frac{f(a+h)−f(a)}{h}\).
- velocidad instantánea
- el cambio de velocidad o dirección en un instante dado; una función\(s(t)\) representa la posición de un objeto en el tiempo\(t\), y la velocidad instantánea o velocidad del objeto en el momento\(t=a\) viene dada por\(s′(a)=\lim \limits_{h \to 0}\frac{s(a+h)−s(a)}{h}\).
- línea secante
- una línea que intersecta dos puntos en una curva
- línea tangente
- una línea que intersecta una curva en un solo punto