13.1: Ángulos
- Page ID
- 121498
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Dibuja ángulos en posición estándar.
- Convertir entre grados y radianes.
- Encuentra ángulos coterminales.
- Encuentra la longitud de un arco circular.
- Utilice la velocidad lineal y angular para describir el movimiento en una trayectoria circular.
Un golfista se balancea para golpear una pelota sobre una trampa de arena y sobre el green. Un piloto de aerolínea maniobra un avión hacia una pista estrecha. Un diseñador de vestimenta crea la última moda. ¿Qué tienen en común todos ellos? Todos trabajan con ángulos, y también todos nosotros en un momento u otro. A veces necesitamos medir ángulos exactamente con instrumentos. Otras veces los estimamos o los juzgamos a ojo. De cualquier manera, el ángulo adecuado puede marcar la diferencia entre el éxito y el fracaso en muchas empresas. En esta sección, examinaremos las propiedades de los ángulos.
Ángulos de dibujo en posición estándar
Definir correctamente un ángulo primero requiere que definamos un rayo. Un rayo consiste en un punto en una línea y todos los puntos que se extienden en una dirección desde ese punto. El primer punto se llama el punto final del rayo. Podemos referirnos a un rayo específico indicando su punto final y cualquier otro punto sobre él. El rayo en la Figura se\(\PageIndex{1}\) puede nombrar como rayo EF, o en forma de símbolo\(\overrightarrow{EF}\).
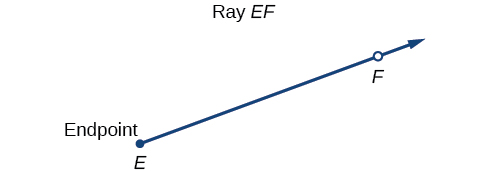
Un ángulo es la unión de dos rayos que tienen un punto final común. El punto final se llama el vértice del ángulo, y los dos rayos son los lados del ángulo. El ángulo en la Figura\(\PageIndex{2}\) se forma a partir de\(\overrightarrow{ED}\) y\(\overrightarrow{EF}\). Los ángulos se pueden nombrar usando un punto en cada rayo y el vértice, como el ángulo DEF, o en forma de símbolo\(∠DEF.\)
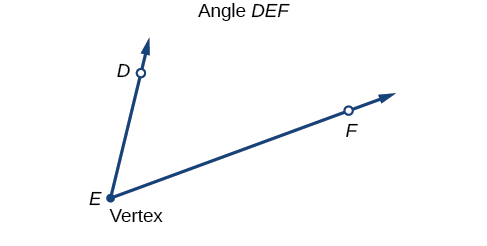
Las letras griegas se utilizan a menudo como variables para la medida de un ángulo. Tabla\(\PageIndex{1}\) es una lista de letras griegas comúnmente utilizadas para representar ángulos, y un ángulo de muestra se muestra en la Figura\(\PageIndex{3}\).
| \(θ\) | \(φ \text{ or }ϕ\) | \(α\) | \(β\) | \(γ\) |
| theta | phi | alfa | beta | gamma |
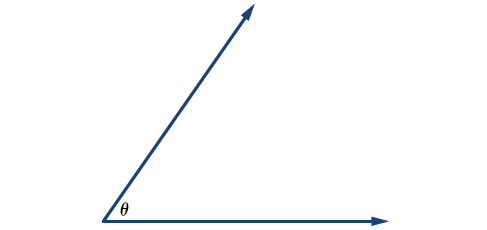
Figura \(\PageIndex{3}\): Ángulo theta, mostrado como\(∠θ\)
La creación de ángulos es un proceso dinámico. Comenzamos con dos rayos acostados uno encima del otro. Dejamos uno fijo en su lugar, y giramos el otro. El rayo fijo es el lado inicial, y el rayo girado es el lado terminal. Para identificar los diferentes lados, indicamos la rotación con un pequeño arco y una flecha cerca del vértice como en la Figura\(\PageIndex{4}\).
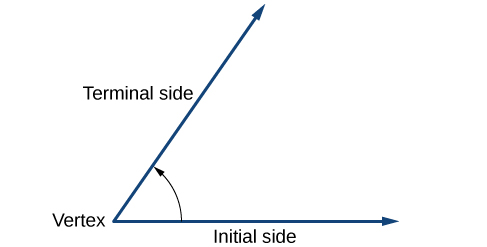
Como comentamos al inicio de la sección, existen muchas aplicaciones para ángulos, pero para poder utilizarlos correctamente, debemos poder medirlos. La medida de un ángulo es la cantidad de rotación desde el lado inicial hasta el lado terminal. Probablemente la unidad más familiar de medición del ángulo es el grado. Un grado es\(\frac{1}{360}\) de rotación circular, por lo que una rotación circular completa contiene 360 grados. Un ángulo medido en grados siempre debe incluir la unidad “grados” después del número, o incluir el símbolo de grado°. Por ejemplo, 90 grados = 90°.
Para formalizar nuestro trabajo, comenzaremos dibujando ángulos en un plano de coordenadas x - y. Los ángulos pueden ocurrir en cualquier posición en el plano de coordenadas, pero para fines de comparación, la convención es ilustrarlos en la misma posición siempre que sea posible. Un ángulo está en posición estándar si su vértice se encuentra en el origen, y su lado inicial se extiende a lo largo del eje x positivo. Ver Figura\(\PageIndex{5}\).
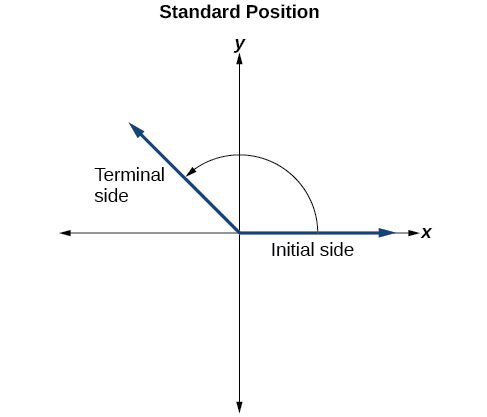
Si el ángulo se mide en sentido contrario a las agujas del reloj desde el lado inicial hasta el lado terminal, se dice que el ángulo es un ángulo positivo. Si el ángulo se mide en sentido horario, se dice que el ángulo es un ángulo negativo.
Dibujar un ángulo en posición estándar siempre comienza de la misma manera: dibuja el lado inicial a lo largo del eje x positivo. Para colocar el lado terminal del ángulo, debemos calcular la fracción de una rotación completa que representa el ángulo. Lo hacemos dividiendo la medida del ángulo en grados por 360°. Por ejemplo, para dibujar un ángulo de 90°, calculamos eso\(\frac{90°}{360°}=\frac{1}{4}\). Entonces, el lado terminal será una cuarta parte del recorrido alrededor del círculo, moviéndose en sentido antihorario desde el eje x positivo. Para dibujar un ángulo de 360°, calculamos eso\(\frac{360°}{360°}=1\). Por lo que el lado terminal será 1 rotación completa alrededor del círculo, moviéndose en sentido antihorario desde el eje x positivo. En este caso, el lado inicial y el lado terminal se solapan. Ver Figura\(\PageIndex{6}\).
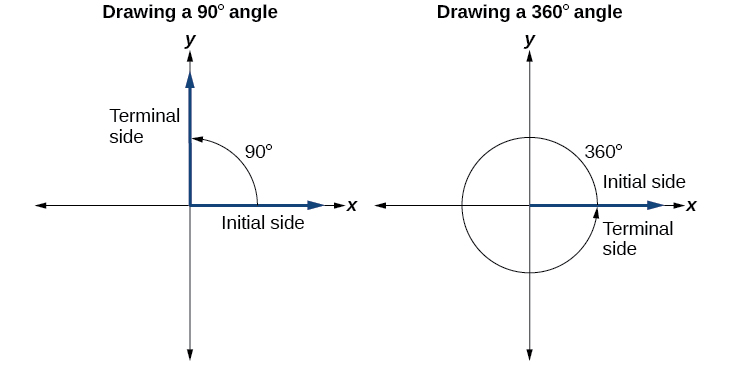
Dado que definimos un ángulo en posición estándar por su lado inicial, tenemos un tipo especial de ángulo cuyo lado terminal se encuentra en un eje, un ángulo cuadrangular. Este tipo de ángulo puede tener una medida de 0°, 90°, 180°, 270° o 360°. Ver Figura\(\PageIndex{7}\).
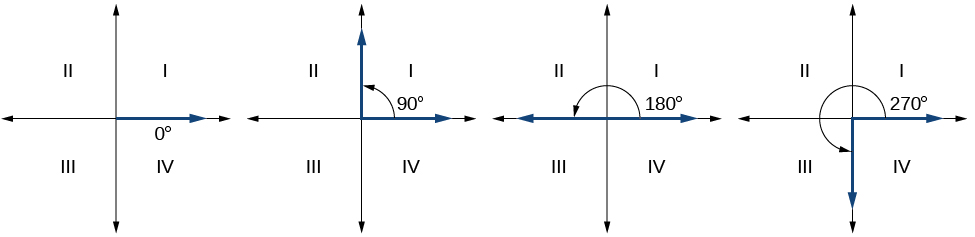
ÁNGULOS CUAR
Los ángulos cuadrangulares son ángulos en posición estándar cuyo lado terminal se encuentra en un eje, incluyendo 0°, 90°, 180°, 270° o 360°.
Dada una medida de ángulo en grados, dibuje el ángulo en posición estándar
- Exprese la medida del ángulo como una fracción de 360°.
- Reduzca la fracción a la forma más simple.
- Dibuja un ángulo que contenga esa misma fracción del círculo, comenzando en el eje x positivo y moviéndose en sentido antihorario para ángulos positivos y en sentido horario para ángulos negativos.
Ejemplo\(\PageIndex{1}\): Drawing an Angle in Standard Position Measured in Degrees
- Esboce un ángulo de 30° en posición estándar.
- Esboce un ángulo de −135° en posición estándar.
Solución
- Divida la medida del ángulo entre 360°.
\[\dfrac{30°}{360°}=\dfrac{1}{12}\]
Para reescribir la fracción en una fracción más familiar, podemos reconocer que
\[\dfrac{1}{12}=\dfrac{1}{3}(\frac{1}{4})\]
Un doceavo equivale a un tercio de cuarto, así que dividiendo un cuarto de rotación en tercios, podemos esbozar una línea a 30° como en la Figura\(\PageIndex{8}\).
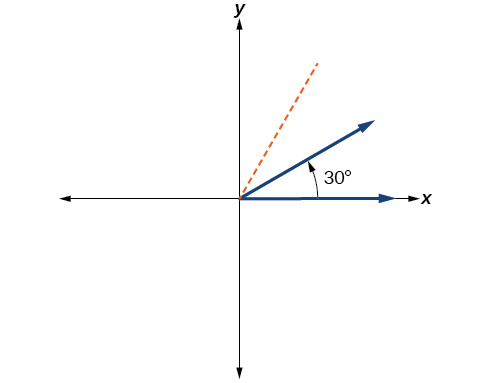
Figura\(\PageIndex{8}\) - Divida la medida del ángulo entre 360°.
\[\dfrac{−135°}{360°}=−\dfrac{3}{8}\]
En este caso, podemos reconocer que
\[−\dfrac{3}{8}=−\dfrac{3}{2}(\dfrac{1}{4})\]
Los tres octavos negativos son una vez y media por cuarto, por lo que colocamos una línea moviéndonos en sentido horario un cuarto completo y medio de otro cuarto, como en la Figura\(\PageIndex{9}\).
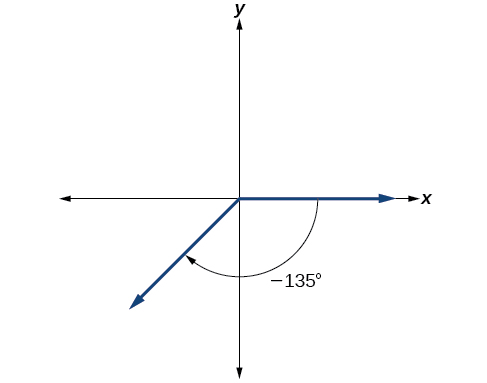
Figura\(\PageIndex{9}\)
\(\PageIndex{1}\):
Mostrar un ángulo de 240° en un círculo en posición estándar.
Solución
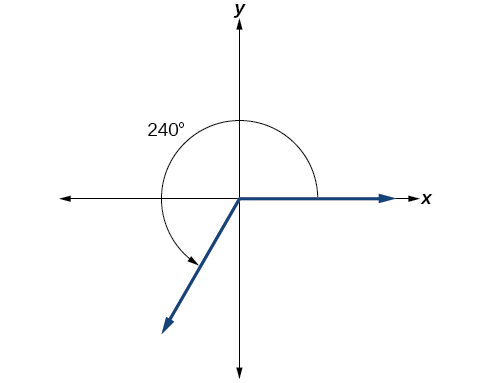
Conversión entre grados y radianes
Dividir un círculo en 360 partes es una elección arbitraria, aunque crea la medida de grado familiar. Podemos elegir otras formas de dividir un círculo. Para encontrar otra unidad, piense en el proceso de dibujar un círculo. Imagina que te detienes antes de que se complete el círculo. A la porción que dibujaste se le conoce como un arco. Un arco puede ser una porción de un círculo completo, un círculo completo o más de un círculo completo, representado por más de una rotación completa. La longitud del arco alrededor de un círculo entero se llama la circunferencia de ese círculo.
La circunferencia de un círculo es\(C=2πr\). Si dividimos ambos lados de esta ecuación por\(r\), creamos la relación entre la circunferencia y el radio, que siempre es\(2π\) independientemente de la longitud del radio. Entonces la circunferencia de cualquier círculo es\(2π≈6.28\) multiplicada por la longitud del radio. Eso significa que si tomamos una cuerda tan larga como el radio y la usamos para medir longitudes consecutivas alrededor de la circunferencia, habría espacio para seis longitudes de cuerda completas y un poco más de un cuarto de séptimo, como se muestra en la Figura\(\PageIndex{11}\).
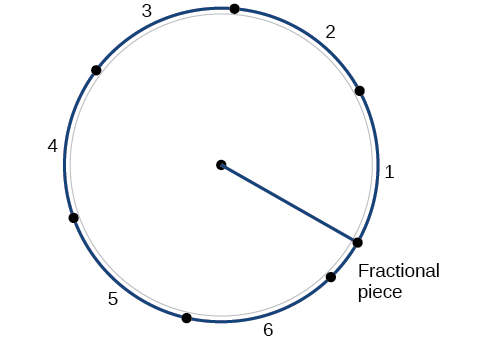
Esto nos lleva a nuestra nueva medida angular. Un radián es la medida de un ángulo central de un círculo que intercepta un arco igual en longitud al radio de ese círculo. Un ángulo central es un ángulo formado en el centro de un círculo por dos radios. Debido a que la circunferencia total es igual a\(2π\) veces el radio, una rotación circular completa es\(2π\) radianes. Entonces
\[\begin{align} 2π \text{ radians } & =360^∘ \\ π \text{ radians } & =\dfrac{360^∘}{2}=180^∘ \\ 1 \text{ radian } & =\dfrac{180^∘}{π}≈57.3^∘ \end{align}\]
Ver Figura\(\PageIndex{12}\). Tenga en cuenta que cuando se describe un ángulo sin una unidad específica, se refiere a la medida de radianes. Por ejemplo, una medida de ángulo de 3 indica 3 radianes. De hecho, la medida del radián es adimensional, ya que es el cociente de una longitud (circunferencia) dividido por una longitud (radio) y las unidades de longitud cancelan.
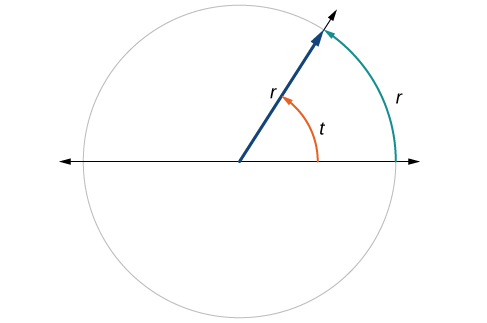
Relacionar longitudes de arco con radio
Una longitud de arco\(s\) es la longitud de la curva a lo largo del arco. Así como la circunferencia completa de un círculo siempre tiene una relación constante con el radio, la longitud del arco producida por cualquier ángulo dado también tiene una relación constante con el radio, independientemente de la longitud del radio.
Esta relación, llamada medida de radianes, es la misma independientemente del radio del círculo, depende solo del ángulo. Esta propiedad nos permite definir una medida de cualquier ángulo como la relación de la longitud del arco s s con el radio\(r\). Ver Figura\(\PageIndex{13}\).
\[\begin{align} s &=rθ \\ θ &=\dfrac{s}{r} \end{align}\]
Si\( s=r\), entonces\(θ=\frac{r}{r}= 1 \text{ radian.}\)
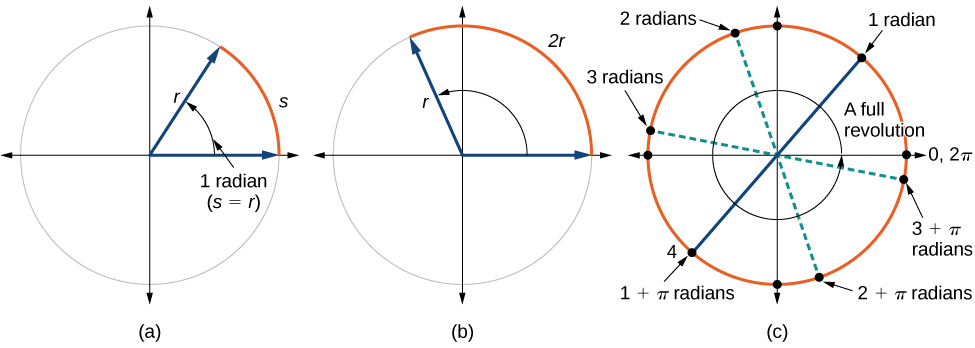
Para elaborar esta idea, considere dos círculos, uno con radio 2 y otro con radio 3. Recordemos la circunferencia de un círculo es\(C=2πr\), donde\(r\) está el radio. El círculo más pequeño entonces tiene circunferencia\(2π(2)=4π\) y el más grande tiene circunferencia\(2π(3)=6π\). Ahora dibujamos un ángulo de 45° sobre los dos círculos, como en la Figura\(\PageIndex{14}\).
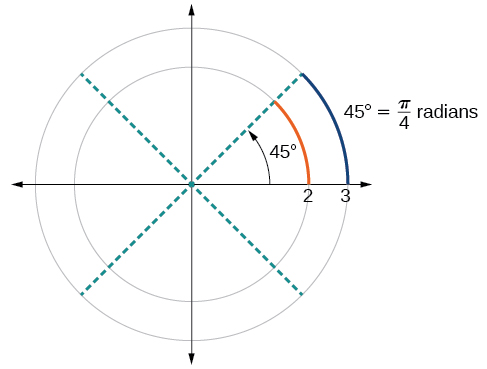
Observe lo que sucede si encontramos la relación de la longitud del arco dividida por el radio del círculo.
\[\begin{align} \text{Smaller circle: } \dfrac{\frac{1}{2}π}{2} & =\dfrac{1}{4}π \\[2mm] \text{Larger circle: } \dfrac{\frac{3}{4}π}{3} & =\dfrac{1}{4}π \end{align}\]
Como ambas relaciones lo son\(\frac{1}{4}π\), las medidas de ángulo de ambos círculos son las mismas, aunque la longitud del arco y el radio difieran.
RADIANES
Un radián es la medida del ángulo central de un círculo de tal manera que la longitud del arco entre el lado inicial y el lado terminal es igual al radio del círculo. Una revolución completa (360°) equivale a\(2\pi\) radianes. Una media revolución (180°) equivale a\(\pi\) radianes.
La medida radianes de un ángulo es la relación entre la longitud del arco subtendido por el ángulo y el radio del círculo. En otras palabras, si\(s\) es la longitud de un arco de un círculo, y\(r\) es el radio del círculo, entonces el ángulo central que contiene ese arco mide\(\frac{s}{r}\) radianes. En un círculo de radio 1, la medida del radián corresponde a la longitud del arco.
Una medida de 1 radián parece ser de aproximadamente 60°. ¿Es eso correcto?
Sí. Es aproximadamente 57.3°. Debido a que \(2π\)radianes es igual a 360°,\(1\) radianes es igual\(\frac{360°}{2π}≈57.3°\).
Uso de radianes
Debido a que la medida de radianes es la relación de dos longitudes, es una medida sin unidades. Por ejemplo, en la Figura\(\PageIndex{14}\), supongamos que el radio fue de 2 pulgadas y la distancia a lo largo del arco también fue de 2 pulgadas. Cuando calculamos la medida radianes del ángulo, las “pulgadas” se cancelan, y tenemos un resultado sin unidades. Por lo tanto, no es necesario escribir la etiqueta “radianes” después de una medida de radianes, y si vemos un ángulo que no está etiquetado con “grados” o el símbolo de grado, podemos suponer que se trata de una medida de radianes.
Considerando el caso más básico, el círculo unitario (un círculo con radio 1), sabemos que 1 rotación equivale a 360 grados, 360°. También podemos rastrear una rotación alrededor de un círculo encontrando la circunferencia,\(C=2πr\), y para el círculo unitario\(C=2π.\) Estas dos formas diferentes de rotar alrededor de un círculo nos dan una forma de convertir de grados a radianes.
\[\begin{array}{clll} 1 \text{rotation } & =360° & =2π & \text{radians} \\[2mm] \dfrac{1}{2} \text{rotation } & =180° & =π & \text{radians} \\[2mm] \dfrac{1}{4} \text{rotation } & =90° & =\dfrac{π}{2} & \text{radians} \end{array}\]
Identificación de ángulos especiales medidos en radianes
Además de conocer las medidas en grados y radianes de un cuarto de revolución, una media revolución y una revolución completa, hay otros ángulos frecuentemente encontrados en una revolución de círculo con los que deberíamos estar familiarizados. Es común encontrar múltiplos de 30, 45, 60 y 90 grados. Estos valores se muestran en la Figura\(\PageIndex{15}\). Memorizar estos ángulos será muy útil ya que estudiamos las propiedades asociadas a los ángulos.
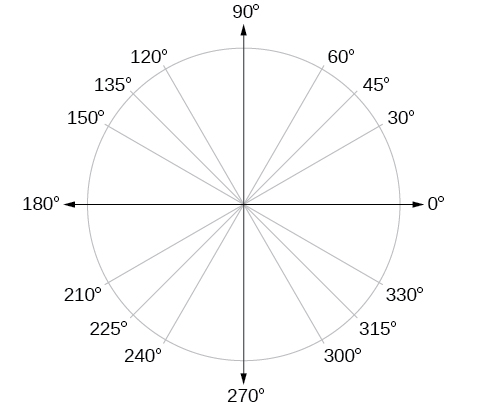
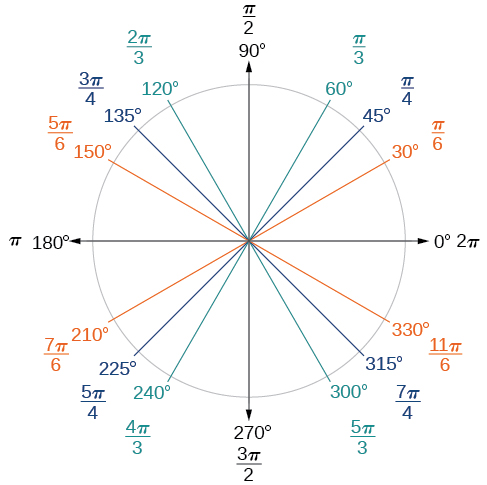
Ahora, podemos enumerar los valores de radianes correspondientes para las medidas comunes de un círculo correspondientes a las enumeradas en la Figura\(\PageIndex{15}\), que se muestran en la Figura\(\PageIndex{16}\). Asegúrate de poder verificar cada una de estas medidas.
Ejemplo\(\PageIndex{2}\): Finding a Radian Measure
Encuentra la medida de radianes de un tercio de una rotación completa.
Solución
Para cualquier círculo, la longitud del arco a lo largo de dicha rotación sería un tercio de la circunferencia. Sabemos que
\[1 \text{ rotation}=2πr\]
Entonces,
\[\begin{align}s &= \dfrac{1}{3}(2πr) \\[2mm] &=\dfrac{2πr}{3} \end{align}\]
La medida del radián sería la longitud del arco dividida por el radio.
\[\begin{align} \text{radian measure} & = \dfrac{\frac{2πr}{3}}{r} \\[2mm] &= \dfrac{2πr}{3r} \\[2mm] & = \dfrac{2π}{3} \end{align}\]
\(\PageIndex{2}\)
Encuentra la medida de radianes de tres cuartas partes de una rotación completa.
Solución
\[\dfrac{3π}{2}\]
Conversión entre radianes y grados
Debido a que grados y radianes miden ambos ángulos, necesitamos poder convertir entre ellos. Podemos hacerlo fácilmente usando una proporción.
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Esta proporción muestra que la medida del ángulo\(θ\) en grados dividido por 180 es igual a la medida del ángulo\(θ\) en radianes dividido por\(π.\) O, dicho de otra manera, grados es a 180 como radianes es a\(π\).
\[\dfrac{\text{Degrees}}{180}=\dfrac{Radians}{π} \]
Conversión entre radianes y grados
Para convertir entre grados y radianes, utilice la proporción
\[\dfrac{θ}{180}=\dfrac{θ^R}{π}\]
Ejemplo\(\PageIndex{3}\): Converting Radians to Degrees
Convertir cada medida de radianes en grados.
- \(\frac{π}{6}\)
- 3
Solución
Debido a que se nos dan radianes y queremos grados, debemos establecer una proporción y resolverla.
- Utilizamos la proporción, sustituyendo la información dada.
\[\begin{align}\dfrac{θ}{180} &=\dfrac{θ^R}{π} \\[2mm] \dfrac{θ}{180} & =\dfrac{\frac{π}{6}}{π} \\ θ & =\dfrac{180}{6} \\ θ & =30^∘ \end{align}\]
- Utilizamos la proporción, sustituyendo la información dada.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{θ}{180} &=\dfrac{3}{π} \\ θ &= \dfrac{3(180)}{π} \\ θ & ≈172^∘ \end{align}\]
\(\PageIndex{3}\)
Convertir\(−\frac{3π}{4}\) radianes a grados.
Solución
−135°
Ejemplo\(\PageIndex{4}\): Converting Degrees to Radians
Convertir\(15\) grados a radianes.
Solución
En este ejemplo, comenzamos con grados y queremos radianes, por lo que nuevamente configuramos una proporción y la resolvemos, pero sustituimos la información dada en una parte diferente de la proporción.
\[\begin{align}\dfrac{θ}{180} &= \dfrac{θ^R}{π} \\ \dfrac{15}{180} &=\dfrac{θ^R}{π} \\ \dfrac{15π}{180} & =θ^R \\ \dfrac{π}{12} & =θ^R \end{align}\]
Análisis
Otra forma de pensar sobre este problema es recordando eso\(30^∘=\frac{π}{6}\). Porque\(15^∘=\frac{1}{2}(30^∘)\),, podemos encontrar que\(\frac{1}{2}(\frac{π}{6})\) es\(\frac{π}{12}\).
\(\PageIndex{4}\)
Convierta 126° en radianes.
Solución
\(\frac{7π}{10}\)
Encontrar ángulos coterminales
La conversión entre grados y radianes puede facilitar el trabajo con ángulos en algunas aplicaciones. Para otras aplicaciones, es posible que necesitemos otro tipo de conversión. Los ángulos negativos y los ángulos mayores que una revolución completa son más incómodos de trabajar que aquellos en el rango de 0° a 360°, o 0 a\(2π\). Sería conveniente reemplazar esos ángulos fuera de rango con un ángulo correspondiente dentro del rango de una sola revolución.
Es posible que más de un ángulo tengan el mismo lado terminal. Mira Figura\(\PageIndex{17}\). El ángulo de 140° es un ángulo positivo, medido en sentido antihorario. El ángulo de —220° es un ángulo negativo, medido en sentido horario. Pero ambos ángulos tienen el mismo lado terminal. Si dos ángulos en posición estándar tienen el mismo lado terminal, son ángulos coterminales. Cada ángulo mayor de 360° o menor de 0° es coterminal con un ángulo entre 0° y 360°, y a menudo es más conveniente encontrar el ángulo coterminal dentro del rango de 0° a 360° que trabajar con un ángulo que está fuera de ese rango.
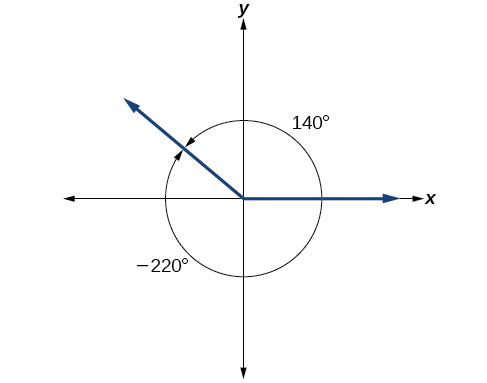
Cualquier ángulo tiene infinitamente muchos ángulos coterminales porque cada vez que sumamos 360° a ese ángulo, o le restamos 360°, el valor resultante tiene un lado terminal en la misma ubicación. Por ejemplo, 100° y 460° son coterminales por esta razón, al igual que −260°. Reconocer que cualquier ángulo tiene infinitamente muchos ángulos coterminales explica la forma repetitiva en las gráficas de las funciones trigonométricas.
El ángulo de referencia de un ángulo es la medida del ángulo más pequeño, positivo y agudo\(t\) formado por el lado terminal del ángulo\(t\) y el eje horizontal. Así, los ángulos de referencia positivos tienen lados terminales que se encuentran en el primer cuadrante y pueden ser utilizados como modelos para ángulos en otros cuadrantes. Ver Figura\(\PageIndex{18}\) para ejemplos de ángulos de referencia para ángulos en diferentes cuadrantes.
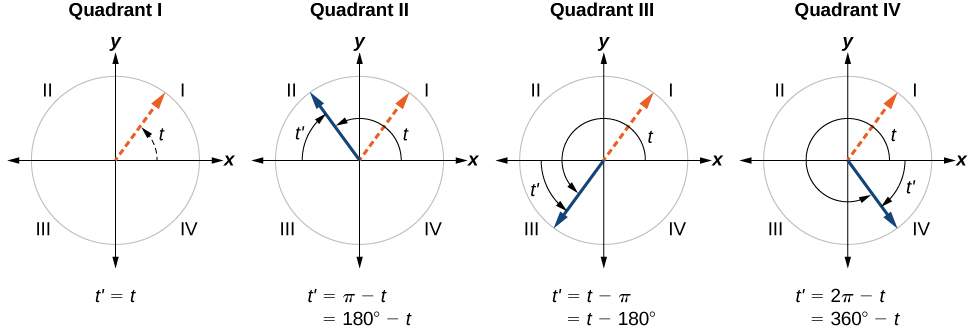
COTERMINAL Y ÁNGULOS
- Los ángulos coterminales son dos ángulos en posición estándar que tienen el mismo lado de terminal.
- El ángulo de referencia de un ángulo es el tamaño del ángulo agudo más pequeño\(t′\), formado por el lado terminal del ángulo\(t\) y el eje horizontal.
Dado un ángulo mayor que 360°, encuentre un ángulo coterminal entre 0° y 360°
- Restar 360° del ángulo dado.
- Si el resultado es aún mayor de 360°, restar 360° nuevamente hasta que el resultado esté entre 0° y 360°.
- El ángulo resultante es coterminal con el ángulo original.
Ejemplo\(\PageIndex{5}\): Finding an Angle Coterminal with an Angle of Measure Greater Than 360°
Encuentra el ángulo mínimo positivo θ que es coterminal con un ángulo que mide 800°, donde\(0°≤θ<360°\).
Solución
Un ángulo con medida 800° es coterminal con un ángulo con medida 800 − 360 = 440°, pero 440° sigue siendo mayor que 360°, por lo que restamos 360° nuevamente para encontrar otro ángulo coterminal: 440 − 360 = 80°.
El ángulo\(θ=80°\) es coterminal con 800°. Para decirlo de otra manera, 800° equivale a 80° más dos rotaciones completas, como se muestra en la Figura\(\PageIndex{19}\).
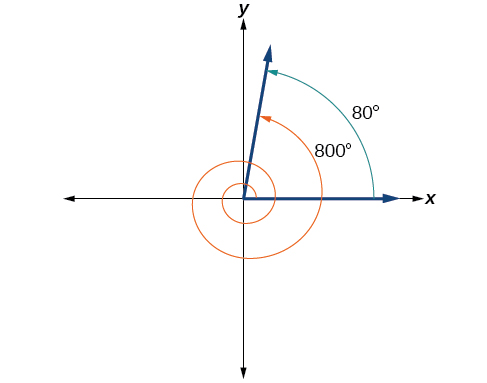
\(\PageIndex{5}\)
Encuentre un ángulo\(α\) que sea coterminal con un ángulo que mida 870°, donde\(0°≤α<360°\).
Solución
\(α=150°\)
Dado un ángulo con medida menor a 0°, encuentre un ángulo coterminal que tenga una medida entre 0° y 360°.
- Agrega 360° al ángulo dado.
- Si el resultado sigue siendo inferior a 0°, agregue 360° nuevamente hasta que el resultado esté entre 0° y 360°.
- El ángulo resultante es coterminal con el ángulo original.
Ejemplo\(\PageIndex{6}\): Finding an Angle Coterminal with an Angle Measuring Less Than 0°
Muestre el ángulo con la medida −45° en un círculo y encuentre un ángulo coterminal positivo α tal que 0° ≤ α < 360°.
Solución
Dado que 45° es la mitad de 90°, podemos comenzar en el eje horizontal positivo y medir la mitad de un ángulo de 90° en el sentido de las agujas del reloj.
Debido a que podemos encontrar ángulos coterminales sumando o restando una rotación completa de 360°, podemos encontrar un ángulo coterminal positivo aquí sumando 360°:
\[−45°+360°=315°\]
Entonces podemos mostrar el ángulo en un círculo, como en la Figura\(\PageIndex{20}\).
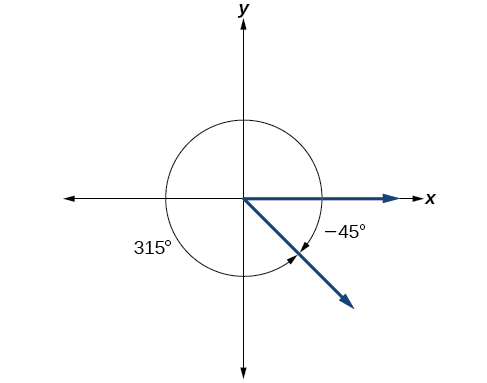
\(\PageIndex{6}\)
Encuentre un ángulo β que sea coterminal con un ángulo que mida −300° tal que\(0°≤β<360°\).
Solución
\(β=60°\)
Encontrar ángulos coterminales medidos en radianes
Podemos encontrar ángulos coterminales medidos en radianes de la misma manera que los hemos encontrado usando grados. En ambos casos, encontramos ángulos coterminales sumando o restando una o más rotaciones completas.
Dado un ángulo mayor que\(2\pi\), find a coterminal angle between 0 and \(2\pi\).
- Restar\(2π\) del ángulo dado.
- Si el resultado es aún mayor que\(2π\), restar de\(2π\) nuevo hasta que el resultado esté entre\(0\) y\(2π\).
- El ángulo resultante es coterminal con el ángulo original.
Ejemplo\(\PageIndex{7}\): Finding Coterminal Angles Using Radians
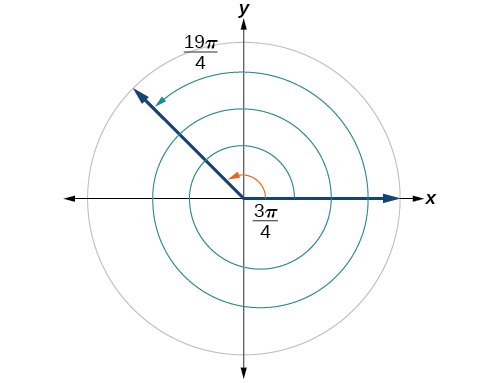
Encuentra un ángulo\(β\) que sea coterminal con\(\frac{19π}{4}\), donde\(0≤β<2π.\)
Solución
Al trabajar en grados, encontramos ángulos coterminales sumando o restando 360 grados, una rotación completa. Asimismo, en radianes, podemos encontrar ángulos coterminales sumando o restando rotaciones completas de\(2π\) radianes:
\[\begin{align} \dfrac{19π}{4}−2π & =\dfrac{19π}{4}−\dfrac{8π}{4} \\ &=\dfrac{11π}{4} \end{align}\]
El ángulo\(\frac{11π}{4}\) es coterminal, pero no menor que\(2π\), así restamos otra rotación:
\[\begin{align} \dfrac{11π}{4}−2π &= \dfrac{11π}{4}−\dfrac{8π}{4} \\ &= \dfrac{3π}{4} \end{align}\]
El ángulo\(\frac{3π}{4}\) es coterminal con\(\frac{19π}{4}\), como se muestra en la Figura\(\PageIndex{21}\).
\(\PageIndex{7}\)
Encuentre un ángulo de medida\(θ\) que sea coterminal con un ángulo de medida\(−\frac{17π}{6}\) donde\(0≤θ<2π.\)
Solución
\(\frac{7π}{6}\)
Determinar la longitud de un arco
Recordemos que la medida radianes\(θ\) de un ángulo se definió como la relación de la longitud\(s\) del arco de un arco circular al radio\(r\) del círculo,\(θ=\frac{s}{r}\). A partir de esta relación, podemos encontrar la longitud del arco a lo largo de un círculo, dado un ángulo.
LARGO DE ARCO EN CIRCULO
En un círculo de radio r, la longitud de un arco\(s\) subtendido por un ángulo con medida\(θ\) en radianes, mostrada en la Figura\(\PageIndex{22}\), es
\[s=rθ\]
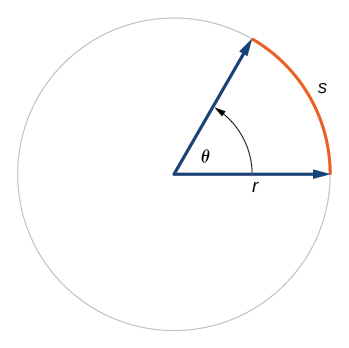
Dado un círculo de radio\(r,\) calculate the length \(s\) of the arc subtended by a given angle of measure \(θ\).
- Si es necesario,\(θ\) conviértelos a radianes.
- Multiplique el radio\(r\) por la medida de radianes de\(θ:s=rθ\).
Ejemplo\(\PageIndex{8}\): Finding the Length of an Arc
Supongamos que la órbita de Mercurio alrededor del sol es un círculo perfecto. Mercurio está aproximadamente a 36 millones de millas del sol.
- En un día de la Tierra, Mercurio completa 0.0114 de su revolución total. ¿Cuántas millas recorre en un día?
- Usa tu respuesta de la parte (a) para determinar la medida de radianes para el movimiento de Mercurio en un día terrestre.
Solución
- Empecemos por encontrar la circunferencia de la órbita de Mercurio.
\[\begin{align} C &=2πr \\ &=2π(\text{36 million miles}) \\ &≈226 \text{ million miles} \end{align}\]
Desde que Mercurio completa 0.0114 de su revolución total en un día terrestre, ahora podemos encontrar la distancia recorrida:
\[(0.0114)226 \text{ million miles} = 2.58 \text{ million miles}\]
- Ahora, convertimos a radianes:
\[\begin{align} \text{radian} & = \dfrac{\text{arc length}}{\text{radius}} \\ &= \dfrac{2.58 \text{ million miles}}{36 \text{ million miles}} \\ & =0.0717 \end{align} \]
\(\PageIndex{8}\)
Encuentra la longitud del arco a lo largo de un círculo de radio 10 unidades subtendidas por un ángulo de 215°.
Solución
\[\dfrac{215π}{18}=37.525 \text{ units} \]
Encontrar el área de un sector de un círculo
Además de la longitud del arco, también podemos usar ángulos para encontrar el área de un sector de un círculo. Un sector es una región de un círculo delimitada por dos radios y el arco interceptado, como una porción de pizza o pastel. Recordemos que el área de un círculo con radio se\(r\) puede encontrar usando la fórmula\(A=πr^2\). Si los dos radios forman un ángulo de\(θ\), medido en radianes, entonces\(\frac{θ}{2π}\) es la relación de la medida del ángulo a la medida de una rotación completa y también es, por lo tanto, la relación entre el área del sector y el área del círculo. Así, el área de un sector es la fracción\(\frac{θ}{2π}\) multiplicada por toda la superficie. (Recuerde siempre que esta fórmula sólo se aplica si\(θ\) está en radianes.)
\[\begin{align} \text{Area of sector} & =(\dfrac{θ}{2π})πr^2 \\ &=\dfrac{θπr^2}{2π} \\ & =\dfrac{1}{2}θr^2 \end{align}\]
ÁREA DE UN SECTOR
El área de un sector de círculo con radio\(r\) subtendido por un ángulo\(θ\), medido en radianes, es
\[A=\dfrac{1}{2}θr^2\]
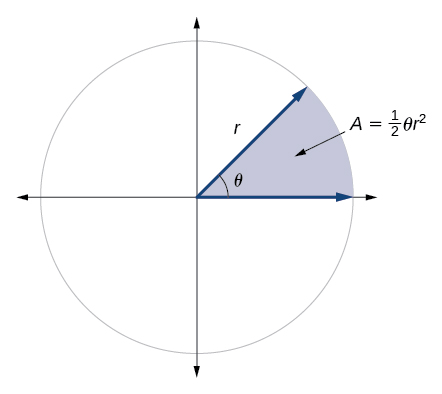
Dado un círculo de radio\(r,\) find the area of a sector defined by a given angle \(θ.\)
- Si es necesario,\(θ\) conviértelos a radianes.
- Multiplica la mitad de la medida del radián\(θ\) por el cuadrado del radio\(r: A=\frac{1}{2}θr^2.\)
Ejemplo\(\PageIndex{9}\): Finding the Area of a Sector
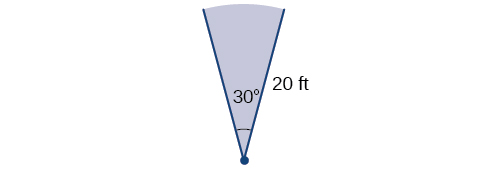
Un aspersor automático para césped rocía una distancia de 20 pies mientras gira 30 grados, como se muestra en la Figura\(\PageIndex{24}\). ¿Cuál es la zona del sector de pasto las aguas de aspersión?
Solución
Primero, necesitamos convertir la medida del ángulo en radianes. Debido a que 30 grados es uno de nuestros ángulos especiales, ya conocemos la medida de radianes equivalente, pero también podemos convertir:
\[\begin{align} \text{30 degrees} &=30⋅\frac{π}{180} \\ &=\frac{π}{6} \text{ radians} \end{align}\]
El área del sector es entonces
\[\begin{align} \text{Area} &= \dfrac{1}{2}(\dfrac{π}{6})(20)^2 \\ & ≈104.72 \end{align}\]
Entonces la zona está a punto\(\mathrm{104.72 \; ft^2}\).
\(\PageIndex{9}\)
En el riego de pivote central, una gran tubería de riego sobre ruedas gira alrededor de un punto central. Un agricultor tiene un sistema de pivote central con un radio de 400 metros. Si las restricciones de agua solo le permiten regar 150 mil metros cuadrados diarios, ¿qué ángulo debería fijar para cubrir el sistema? Escribe la respuesta en medida de radianes a dos decimales.
Solución
1.88
Uso de la velocidad lineal y angular para describir el movimiento en una trayectoria circular
Además de encontrar el área de un sector, podemos usar ángulos para describir la velocidad de un objeto en movimiento. Un objeto que viaja en una trayectoria circular tiene dos tipos de velocidad. La velocidad lineal es la velocidad a lo largo de una trayectoria recta y se puede determinar por la distancia que se mueve (su desplazamiento) en un intervalo de tiempo dado. Por ejemplo, si una rueda con radio de 5 pulgadas gira una vez por segundo, un punto en el borde de la rueda se mueve una distancia igual a la circunferencia, o 10π pulgadas, cada segundo. Entonces la velocidad lineal del punto está\(10π\) en. /s. La ecuación para la velocidad lineal es la siguiente donde\(v\) es velocidad lineal,\(s\) es desplazamiento y\(t\) es tiempo.
\[v=\dfrac{s}{t}\]
La velocidad angular resulta del movimiento circular y puede ser determinada por el ángulo a través del cual un punto gira en un intervalo de tiempo dado. En otras palabras, la velocidad angular es la rotación angular por unidad de tiempo. Entonces, por ejemplo, si un engranaje hace una rotación completa cada 4 segundos, podemos calcular su velocidad angular como\(\frac{360 \text{ degrees}}{4 \text{ seconds}}= \) 90 grados por segundo. La velocidad angular se puede dar en radianes por segundo, rotaciones por minuto o grados por hora, por ejemplo. La ecuación para la velocidad angular es la siguiente, donde\(ω\) (leer como omega) es la velocidad angular,\(θ\) es el ángulo atravesado y\(t\) es el tiempo.
\[ω=\dfrac{θ}{t}\]
Combinando la definición de velocidad angular con la ecuación de longitud de arco\(s=rθ\),, podemos encontrar una relación entre velocidades angulares y lineales. La ecuación de velocidad angular se puede resolver para\(θ\),\(θ=ωt.\) dando Sustituir esto en la ecuación de longitud de arco da:
\[\begin{align}s &=rθ \\ &=rωt \end{align}\]
Sustituyendo esto en la ecuación de velocidad lineal da:
\[\begin{align} v & = \dfrac{s}{t} &=\dfrac{rωt}{t} &=rω \end{align}\]
Velocidad Angular y Lineal
A medida que un punto se mueve a lo largo de un círculo de radio\(r,\) su velocidad angular\(ω\),, es la rotación angular\(θ\) por unidad de tiempo,\(t\).
\[ω=\dfrac{θ}{t}\]
La velocidad lineal. \(v\), del punto se puede encontrar como la distancia recorrida, longitud del arco\(s\), por unidad de tiempo,\(t.\)
\[v=\frac{s}{t}\]
Cuando la velocidad angular se mide en radianes por unidad de tiempo, la velocidad lineal y la velocidad angular están relacionadas por la ecuación
\[v=rω\]
Esta ecuación establece que la velocidad angular en radianes\(ω\), que representa la cantidad de rotación que se produce en una unidad de tiempo, se puede multiplicar por el radio\(r\) para calcular la longitud total del arco recorrida en una unidad de tiempo, que es la definición de velocidad lineal.
Dada la cantidad de rotación angular y el tiempo transcurrido, calcular la velocidad angular
- Si es necesario, convierta la medida del ángulo en radianes.
- Divida el ángulo en radianes por el número de unidades de tiempo transcurridas:\(ω=\frac{θ}{t}.\)
- La velocidad resultante será en radianes por unidad de tiempo.
Ejemplo\(\PageIndex{10}\): Finding Angular Speed
Una rueda hidráulica, mostrada en la Figura\(\PageIndex{25}\), completa 1 rotación cada 5 segundos. Encuentra la velocidad angular en radianes por segundo.
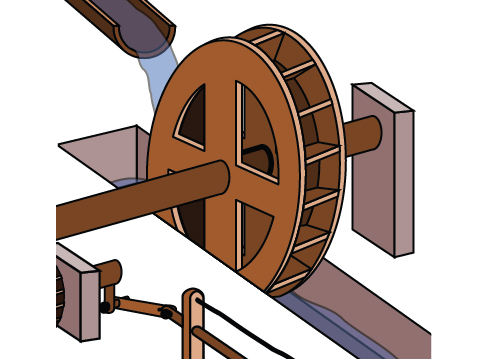
Solución
La rueda completa 1 rotación, o pasa por un ángulo de\(2π\) radianes en 5 segundos, por lo que la velocidad angular sería\(ω=\frac{2π}{5}≈1.257\) radianes por segundo.
\(\PageIndex{10}\)
Un disco de vinilo antiguo se reproduce en una plataforma giratoria que gira en sentido horario a una velocidad de 45 rotaciones por minuto. Encuentra la velocidad angular en radianes por segundo.
Solución
\(−\frac{3π}{2}\)rad/s
Dado el radio de un círculo, un ángulo de rotación y una longitud de tiempo transcurrido, determinar la velocidad lineal
- Convertir la rotación total a radianes si es necesario.
- Divida la rotación total en radianes por el tiempo transcurrido para encontrar la velocidad angular: aplicar\(ω=\frac{θ}{t}\).
- Multiplique la velocidad angular por la longitud del radio para encontrar la velocidad lineal, expresada en términos de la unidad de longitud utilizada para el radio y la unidad de tiempo utilizada para el tiempo transcurrido: aplicar\(v=rω\).
Ejemplo\(\PageIndex{11}\): Finding a Linear Speed
Una bicicleta tiene ruedas de 28 pulgadas de diámetro. Un tacómetro determina que las ruedas están girando a 180 RPM (revoluciones por minuto). Encuentra la velocidad que recorre la bicicleta por la carretera.
Solución
Aquí, tenemos una velocidad angular y necesitamos encontrar la velocidad lineal correspondiente, ya que la velocidad lineal del exterior de las llantas es la velocidad a la que la bicicleta viaja por la carretera.
Comenzamos por convertir de rotaciones por minuto a radianes por minuto. Puede ser útil utilizar las unidades para realizar esta conversión:
\[\mathrm{180 \dfrac{\cancel{rotations}}{minute}⋅\dfrac{2π \; radians}{\cancel{rotation}}=360π\dfrac{radians}{minute}}\]
Usando la fórmula desde arriba junto con el radio de las ruedas, podemos encontrar la velocidad lineal:
\[\begin{align} v & =(14 \text{ inches})(360π \dfrac{\text{radians}}{\text{minute}}) \\ &=5040π \dfrac{\text{inches}}{\text{minute}} \end{align}\]
Recuerde que los radianes son una medida sin unidades, por lo que no es necesario incluirlos.medida sin unidades, por lo que no es necesario incluirlos.
Finalmente, es posible que deseemos convertir esta velocidad lineal en una medición más familiar, como millas por hora.
\[\mathrm{5040π\dfrac{\cancel{inches}}{\cancel{minute}}⋅\dfrac{1 \; \cancel{ feet}}{12 \; \cancel{ inches}}⋅\dfrac{1 \; \cancel{ mile}}{5280 \cancel{ feet}}⋅\dfrac{60 \cancel{ minutes}}{1 \; hour}≈14.99 \; miles \; per \; hour \; (mph)}\]
![]() \(\PageIndex{11}\)
\(\PageIndex{11}\)
Un satélite gira alrededor de la Tierra a 0.25 radianes por hora a una altitud de 242 km sobre la Tierra. Si el radio de la Tierra es de 6378 kilómetros, encuentra la velocidad lineal del satélite en kilómetros por hora.
Solución
1655 kilómetros por hora
Medios
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con ángulos, longitud de arco y áreas de sectores.
Ecuaciones Clave
| longitud del arco | \(s=rθ\) |
| area of a sector | \(A=\frac{1}{2}θr^2\) |
| angular speed | \(ω=\frac{θ}{t}\) |
| linear speed | \(v=\frac{s}{t}\) |
| linear speed related to angular speed | \(v=rω\) |
Key Concepts
- An angle is formed from the union of two rays, by keeping the initial side fixed and rotating the terminal side. The amount of rotation determines the measure of the angle.
- An angle is in standard position if its vertex is at the origin and its initial side lies along the positive x-axis. A positive angle is measured counterclockwise from the initial side and a negative angle is measured clockwise.
- To draw an angle in standard position, draw the initial side along the positive x-axis and then place the terminal side according to the fraction of a full rotation the angle represents. See Example.
- In addition to degrees, the measure of an angle can be described in radians. See Example.
- To convert between degrees and radians, use the proportion \(\frac{θ}{180}=\frac{θ^R}{π}\). See Example and Example.
- Two angles that have the same terminal side are called coterminal angles.
- We can find coterminal angles by adding or subtracting 360° or \(2π\). See Example and Example.
- Coterminal angles can be found using radians just as they are for degrees. See Example.
- The length of a circular arc is a fraction of the circumference of the entire circle. See Example.
- The area of sector is a fraction of the area of the entire circle. See Example.
- An object moving in a circular path has both linear and angular speed.
- The angular speed of an object traveling in a circular path is the measure of the angle through which it turns in a unit of time. See Example.
- The linear speed of an object traveling along a circular path is the distance it travels in a unit of time. See Example.
Glossary
- angle
- the union of two rays having a common endpoint
- angular speed
- the angle through which a rotating object travels in a unit of time
- arc length
- the length of the curve formed by an arc
- area of a sector
- area of a portion of a circle bordered by two radii and the intercepted arc; the fraction \(\frac{θ}{2π}\) multiplied by the area of the entire circle
- coterminal angles
- description of positive and negative angles in standard position sharing the same terminal side
- degree
- a unit of measure describing the size of an angle as one-360th of a full revolution of a circle
- initial side
- the side of an angle from which rotation begins
- linear speed
- the distance along a straight path a rotating object travels in a unit of time; determined by the arc length
- measure of an angle
- the amount of rotation from the initial side to the terminal side
- negative angle
- description of an angle measured clockwise from the positive x-axis
- positive angle
- description of an angle measured counterclockwise from the positive x-axis
- quadrantal angle
- an angle whose terminal side lies on an axis
- radian measure
- the ratio of the arc length formed by an angle divided by the radius of the circle
- radian
- the measure of a central angle of a circle that intercepts an arc equal in length to the radius of that circle
- ray
- one point on a line and all points extending in one direction from that point; one side of an angle
- reference angle
- the measure of the acute angle formed by the terminal side of the angle and the horizontal axis
- standard position
- the position of an angle having the vertex at the origin and the initial side along the positive x-axis
- terminal side
- the side of an angle at which rotation ends
- vertex
- the common endpoint of two rays that form an angle


