2.3: Ejercicios

Última actualización
Guardar como PDF

Page ID: 117642

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

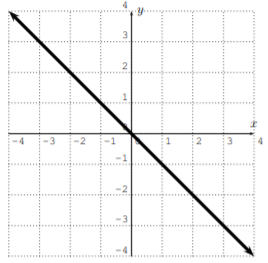
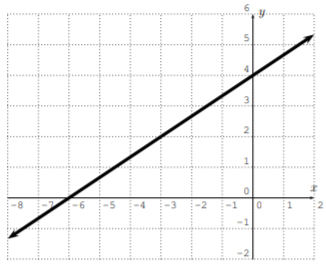
$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Ejercicio$\PageIndex{1}$

Encuentra la pendiente y$y$ -intercepción de la línea con los datos dados. Usando la pendiente y la$y$ intercepción, escriba la ecuación de la línea en forma de pendiente-intercepción.

$clipboard_e318400c74b8133f5d54538d3902259b4.png$
$clipboard_e644881baf19ea5dccb82bc63a4c866aa.png$
$clipboard_ebd8d0d9306e5cce26f621aaeb8a3ed45.png$
$clipboard_ea6e6ddcaa9fbabc2fd17377cb2c453b4.png$
$clipboard_e629093ace6be250fe7da1f2ef8ec0b78.png$
$clipboard_ea94d51d9dbffdcdc177d652d4fc5e212.png$

Contestar

$y=2 x-4$
$y=-x+3$
$y=-2 x-2$
$y=\dfrac{2}{5} x+3$
$y=-x+0$o$ y=-x$
$y=\dfrac{2}{3} x+4$

Ejercicio$\PageIndex{2}$

Escribe la ecuación de la línea en forma de pendiente-intercepción. Identificar pendiente e$y$ -intercepción de la línea.

$4x+2y=8$
$9x-3y+15=0$
$-5x-10y=20$
$3x-5y=7$
$-12x+8y=-60$
$8x-9y=0$

Contestar

$y=-2 x+4$
$y=3 x+5$
$y=-\dfrac{1}{2} x-2$
$y=\dfrac{3}{5} x-\dfrac{7}{5}$
$y=\dfrac{3}{2} x-\dfrac{15}{2}$
$y=\dfrac{8}{9} x$

Ejercicio$\PageIndex{3}$

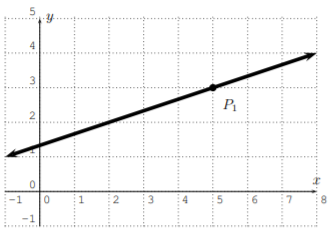
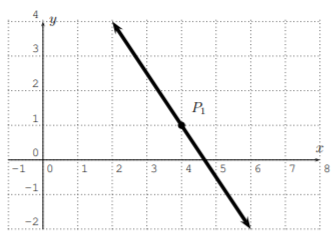
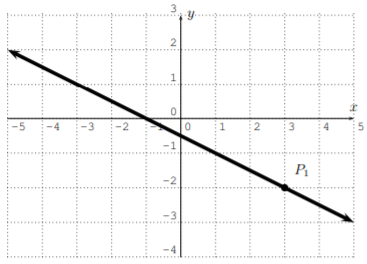
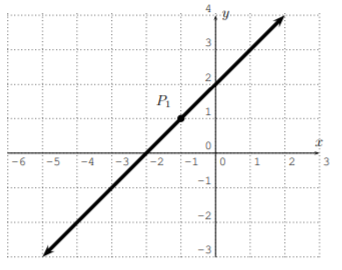
Encuentra la ecuación de la línea en forma de punto-pendiente (Ec. 2.1.2) usando el punto indicado$P_1$.

$clipboard_e4d7102ca496b46fcc59f315443809661.png$
$clipboard_e4aa0af83089f4852c3aed54307e42ff1.png$
$clipboard_e93252049b0fea51e6f36ec3f8b369e97.png$
$clipboard_e5dca3249a1618870f8b71f5e1c0cb17d.png$

Contestar

$y-3=\dfrac{1}{3} \cdot(x-5)$
$y-1=-\dfrac{3}{2} \cdot(x-4)$
$y+2=-\dfrac{1}{2} \cdot(x-3)$
$y-1=1 \cdot(x+1)$

Ejercicio$\PageIndex{4}$

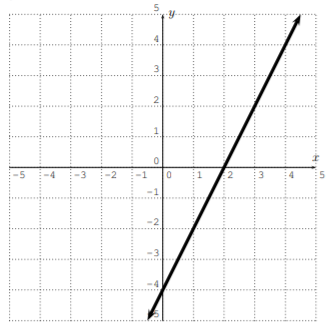
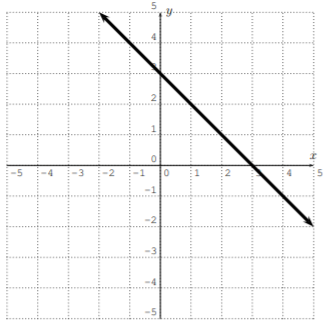
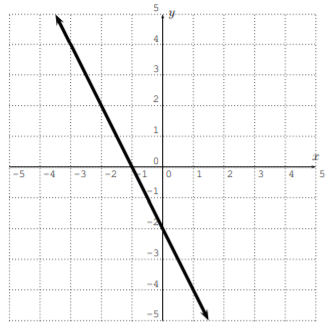
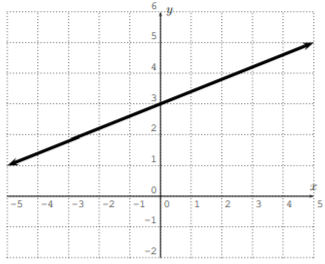
Grafica la línea calculando una tabla (como en el Ejemplo 2.1.1). (Resolver por$y$ primera vez, si esto es necesario.)

$y=2x-4$
$y=-x+4$
$y=\dfrac 1 2 x +1$
$y=3x$
$8x-4y=12$
$x+3y+6=0$

Contestar

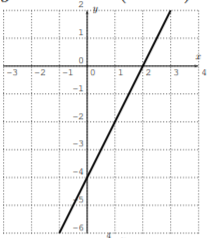
$clipboard_e4c044161514756ec1e7786773980ed30.png$
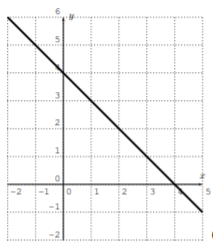
$clipboard_e5abf21dde77b75257522e738b8b9959a.png$
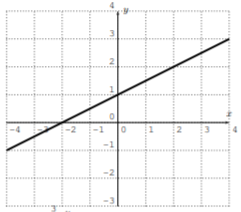
$clipboard_ef18304d9f3209f0a3617e354eb72f6e5.png$
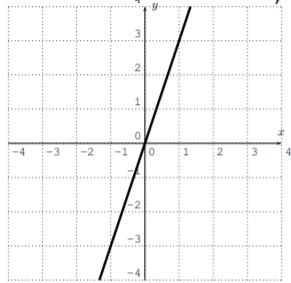
$clipboard_eb23e2d6bce50dcc6ffad8f14aea20106.png$
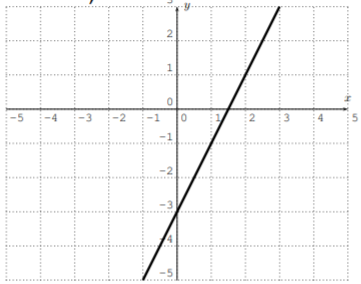
$y=2 x-3$ $clipboard_e283a895c36e660c40df34db980960804.png$
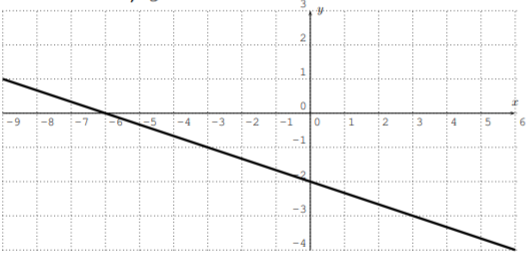
$y=-\dfrac{1}{3} x-2$ $clipboard_e4282772e8f7562c5bac61f03883fce0b.png$

Ejercicio$\PageIndex{5}$

Determine si la tabla dada describe una función. Si es así, determinar su dominio y rango. Describir qué salidas se asignan a qué entradas.

\ [\ begin {array} {|c||c|c|c|c|c|}
\ hline x & -5 & 3 & -1 & 6 & 0\\ hline
\ hline\ hline y & 5 & 2 & 8 & 3 & 7\
\ hline
\ end {array}\ nonumber\]
\ [\ begin {array} {|c||c|c|c|c|c|}
\ hline x & 6 & 17 & 4 & -2 & 4\\ hline
\ hline\ hline y & 8 & -2 & 0 & 3 & -1\
\ hline
\ end {array}\ nonumber\]
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & 19 & 7 & 6 & -2 & 3 & -11\\
\ hline\ hline\ hline y & 3 & 3 & 3 & 3 & 3 & 3
\\ hline
\ end {array}\ nonumber\]
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & 1 & 2 & 3 & 3 & 4 & 5\
\ hline\ hline\ hline y & 5.33 & 9 & 13 & 13 & 17 &\ sqrt {19}\
\\ hline
\ end {array}\ nonumber\]
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & 0 & 1 & 2 & 2 & 2 & 3 & 4\
\\ hline\ hline\ hline y & 0 & 1 & 2 & 3 & 3 & 4
\\ hline
\ end {array}\ nonumber\]

Contestar

esta es una función con dominio$D=\{-5,-1,0,3,6\}$ y rango$R = \{2, 3, 5, 7, 8\}$, por ejemplo: la entrada$x = −5$ da salida$y = 5$, etc.
no es una función ya que para$x = 4$ tenemos ambos$y = 0$ y$y = −1$
esta es una función con$D = \{−11, −2, 3, 6, 7, 19\}$,$R = \{3\}$
esta es una función con$D=\{1,2,3,4,5\}, R=\{\sqrt{19}, 5.33,9,13,17\}$
esto no es una función

Ejercicio$\PageIndex{6}$

Consideramos a los niños y a sus madres (de nacimiento).

¿El hijo asignado a su madre biológica constituye una función (en el sentido de Definición como aquí se afirma)?
¿Constituye una función la madre asignada a sus hijos?
En el caso de que la asignación sea una función, ¿cuál es el dominio?
En el caso de que la asignación sea una función, ¿cuál es el rango?

Contestar

si
no
el dominio para la función en (a) es el conjunto de todos los hijos
el rango para la función en (a) es el conjunto de todas las madres

Ejercicio$\PageIndex{7}$

Un banco ofrece a los clientes adinerados una cierta cantidad de interés, si mantienen más de un$1$ millón de dólares en su cuenta. El monto se describe en la siguiente tabla:

\ [\ begin {array} {|c||c|}
\ hline\ text {cantidad en dólares} x\ texto {en la cuenta} &\ text {cantidad de interés}\
\\ hline\ hline\ hline x\ leq\ $1.000.000 &
\ $0\\ hline\ $ 1.000.000<x\ leq\ $10.000.000 & 2\%\ text {de} x\
\ hline\ $10,000 ,000<x & 1\%\ texto {de} x\
\ hline
\ end {array}\ nonumber\]

Justificar que el monto de efectivo de asignación a intereses define una función.
Encuentra el interés por una cantidad de:
1. $\$50,000$
2. $\$5,000,000$
3. $\$1,000,000$
4. $\$30,000,000$
5. $\$10,000,000$
6. $\$2,000,000$

Contestar

un monto en efectivo determinado$x$ determina el monto de interés$y$
i)$\$0$, ii)$\$100,000$, iii)$\$0$, iv)$\$300,000$, v)$\$200,000$, vi)$\$40,000$

Ejercicio$\PageIndex{8}$

Encuentre una fórmula para una función que describa las entradas y salidas dadas.

entrada: el radio de un círculo, salida: la circunferencia del círculo
entrada: la longitud lateral en un triángulo equilátero, salida: el perímetro del triángulo
entrada: una longitud lateral de un rectángulo, siendo la otra longitud lateral$3$, salida: el perímetro del rectángulo
entrada: la longitud lateral de un cubo, salida: el volumen del cubo

Contestar

$C=2 \pi r$
$P=3 a$
$P=2 a+6$
$V=a^{3}$

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)