9.1: Gráficas de polinomios
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\id}{\mathrm{id}} \newcommand{\Span}{\mathrm{span}}
( \newcommand{\kernel}{\mathrm{null}\,}\) \newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}} \newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}} \newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\id}{\mathrm{id}}
\newcommand{\Span}{\mathrm{span}}
\newcommand{\kernel}{\mathrm{null}\,}
\newcommand{\range}{\mathrm{range}\,}
\newcommand{\RealPart}{\mathrm{Re}}
\newcommand{\ImaginaryPart}{\mathrm{Im}}
\newcommand{\Argument}{\mathrm{Arg}}
\newcommand{\norm}[1]{\| #1 \|}
\newcommand{\inner}[2]{\langle #1, #2 \rangle}
\newcommand{\Span}{\mathrm{span}} \newcommand{\AA}{\unicode[.8,0]{x212B}}
\newcommand{\vectorA}[1]{\vec{#1}} % arrow
\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow
\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vectorC}[1]{\textbf{#1}}
\newcommand{\vectorD}[1]{\overrightarrow{#1}}
\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}
\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}
\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }
\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}
\newcommand{\avec}{\mathbf a} \newcommand{\bvec}{\mathbf b} \newcommand{\cvec}{\mathbf c} \newcommand{\dvec}{\mathbf d} \newcommand{\dtil}{\widetilde{\mathbf d}} \newcommand{\evec}{\mathbf e} \newcommand{\fvec}{\mathbf f} \newcommand{\nvec}{\mathbf n} \newcommand{\pvec}{\mathbf p} \newcommand{\qvec}{\mathbf q} \newcommand{\svec}{\mathbf s} \newcommand{\tvec}{\mathbf t} \newcommand{\uvec}{\mathbf u} \newcommand{\vvec}{\mathbf v} \newcommand{\wvec}{\mathbf w} \newcommand{\xvec}{\mathbf x} \newcommand{\yvec}{\mathbf y} \newcommand{\zvec}{\mathbf z} \newcommand{\rvec}{\mathbf r} \newcommand{\mvec}{\mathbf m} \newcommand{\zerovec}{\mathbf 0} \newcommand{\onevec}{\mathbf 1} \newcommand{\real}{\mathbb R} \newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]} \newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]} \newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]} \newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]} \newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]} \newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]} \newcommand{\laspan}[1]{\text{Span}\{#1\}} \newcommand{\bcal}{\cal B} \newcommand{\ccal}{\cal C} \newcommand{\scal}{\cal S} \newcommand{\wcal}{\cal W} \newcommand{\ecal}{\cal E} \newcommand{\coords}[2]{\left\{#1\right\}_{#2}} \newcommand{\gray}[1]{\color{gray}{#1}} \newcommand{\lgray}[1]{\color{lightgray}{#1}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\row}{\text{Row}} \newcommand{\col}{\text{Col}} \renewcommand{\row}{\text{Row}} \newcommand{\nul}{\text{Nul}} \newcommand{\var}{\text{Var}} \newcommand{\corr}{\text{corr}} \newcommand{\len}[1]{\left|#1\right|} \newcommand{\bbar}{\overline{\bvec}} \newcommand{\bhat}{\widehat{\bvec}} \newcommand{\bperp}{\bvec^\perp} \newcommand{\xhat}{\widehat{\xvec}} \newcommand{\vhat}{\widehat{\vvec}} \newcommand{\uhat}{\widehat{\uvec}} \newcommand{\what}{\widehat{\wvec}} \newcommand{\Sighat}{\widehat{\Sigma}} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9}Ahora discutimos la forma de las gráficas de funciones polinómicas. Recordemos que una función polinómicaf de gradon es una función de la forma
f(x)=a_n x^n+a_{n-1} x^{n-1}+\dots +a_2 x^2+ a_1 x + a_0 \nonumber
Ya sabemos por la Sección 2.1, que las gráficas de polinomiosf(x)=ax+b de grado1 son líneas rectas.
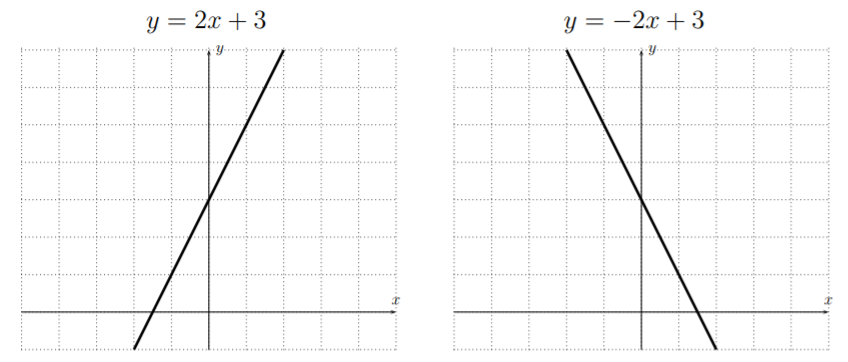
Los polinomios de grado1 tienen una sola raíz.
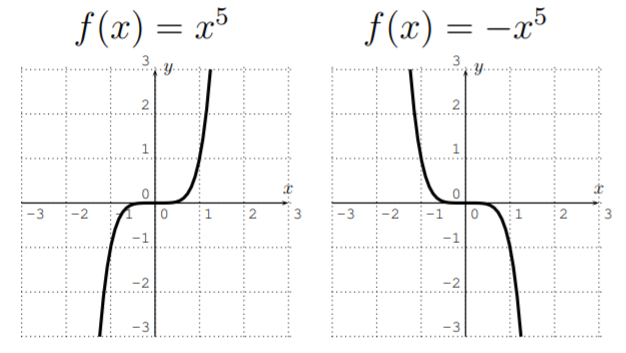
También es fácil bosquejar las gráficas de funcionesf(x)=x^n.
Graficandoy=x^2,y=x^3y=x^4,y=x^5,, obtenemos:
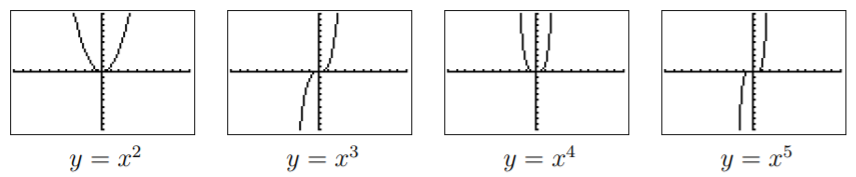
A partir de esto, vemos que la forma de la gráfica def(x)=x^n depende den ser par o impar.
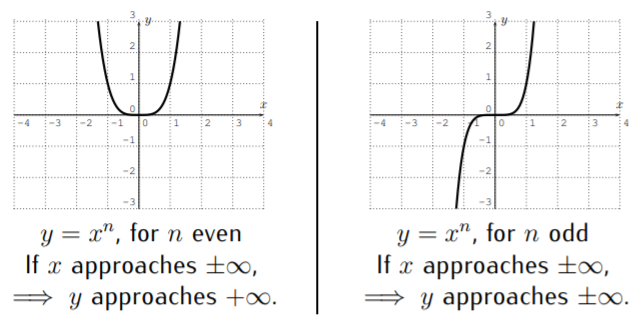
Ahora hacemos algunas observaciones sobre gráficas de polinomios generales de grados2,3,45, y, más generalmente, de cualquier gradon. En particular, nos interesará el número de raíces y el número de extrema (es decir, el número de máximos o mínimos) de la gráfica de un polinomiof.
Dejarf(x)=ax^2+bx+c ser un polinomio de grado2. La gráfica def es una parábola.
- ftiene como máximo2 raíces. ftiene un extremo (es decir, un máximo o mínimo).
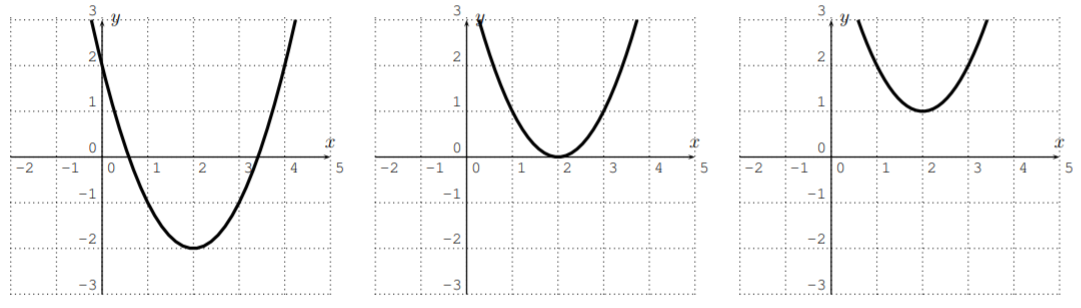
- Sia>0 entoncesf se abre hacia arriba, sia<0 entoncesf se abre hacia abajo.
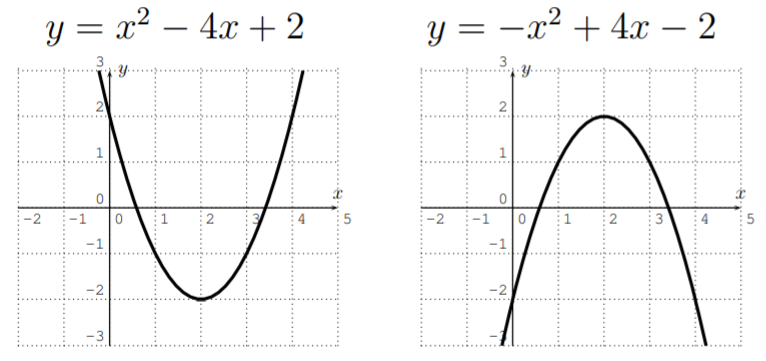
Dejarf(x)=ax^3+bx^2+cx+d ser un polinomio de grado3. La gráfica puede cambiar su dirección como máximo dos veces.
- ftiene como máximo3 raíces. ftiene a lo sumo2 extrema.
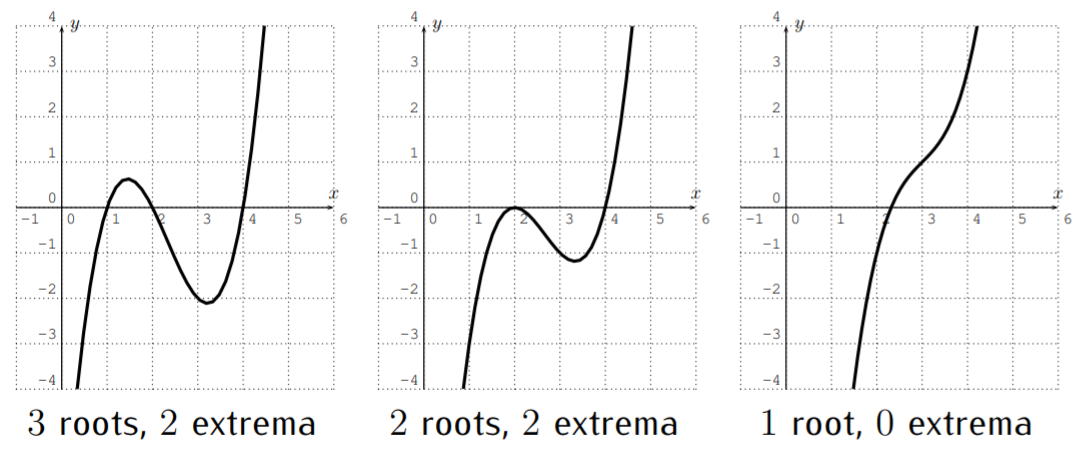
- Sia>0 entonces+\infty sef(x) acerca cuando sex acerca+\infty (es decir,f(x) se hace grande cuandox se hace grande), yf(x) se acerca-\infty cuando sex acerca-\infty. Sia<0 entonces sef(x) acerca-\infty cuando sex acerca+\infty, y+\infty sef(x) acerca cuando sex acerca-\infty.
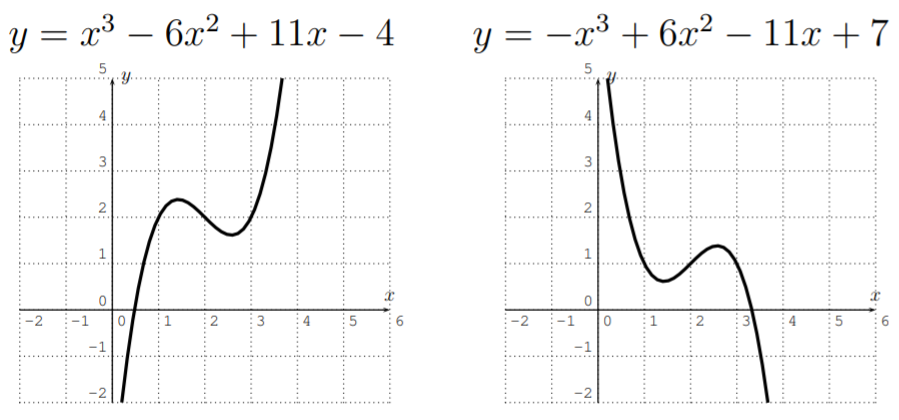
Arriba, tenemos una primera instancia de un polinomio de gradon que “cambia su dirección” una vez más que un polinomio de un grado menorn-1. A continuación, damos ejemplos de este fenómeno para grados superiores también.
Dejarf(x)=ax^4+bx^3+cx^2+dx+e ser un polinomio de grado4.
- ftiene como máximo4 raíces. ftiene a lo sumo3 extrema. Sia>0 entoncesf se abre hacia arriba, sia<0 entoncesf se abre hacia abajo.
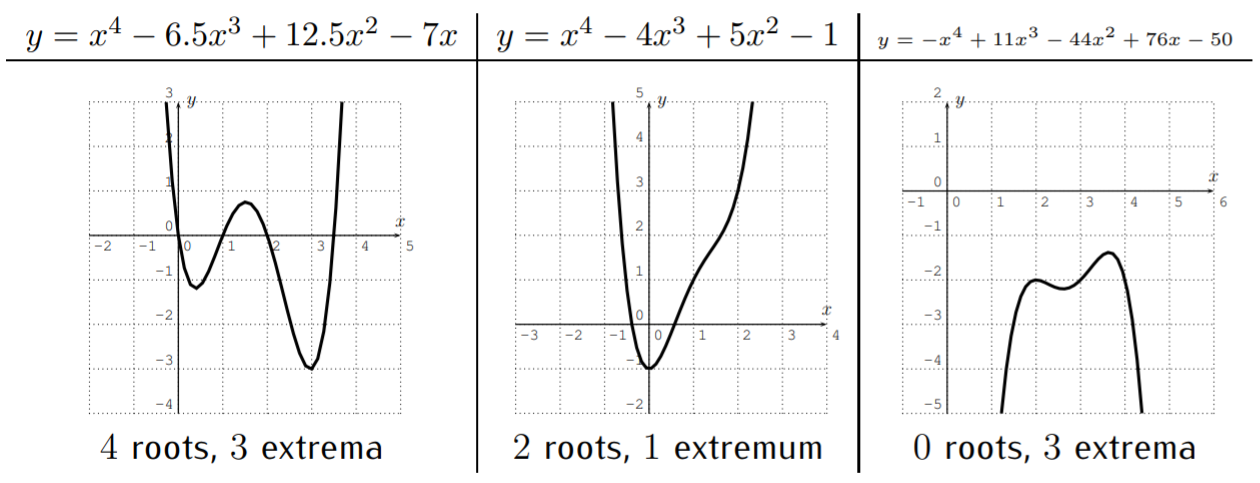
Dejarf ser un polinomio de grado5.
- ftiene como máximo5 raíces. ftiene a lo sumo4 extrema. Sia>0 entonces sef(x) acerca+\infty cuando sex acerca+\infty, y-\infty sef(x) acerca cuando sex acerca-\infty. Sia<0 entonces sef(x) acerca-\infty cuando sex acerca+\infty, y+\infty sef(x) acerca cuando sex acerca-\infty.
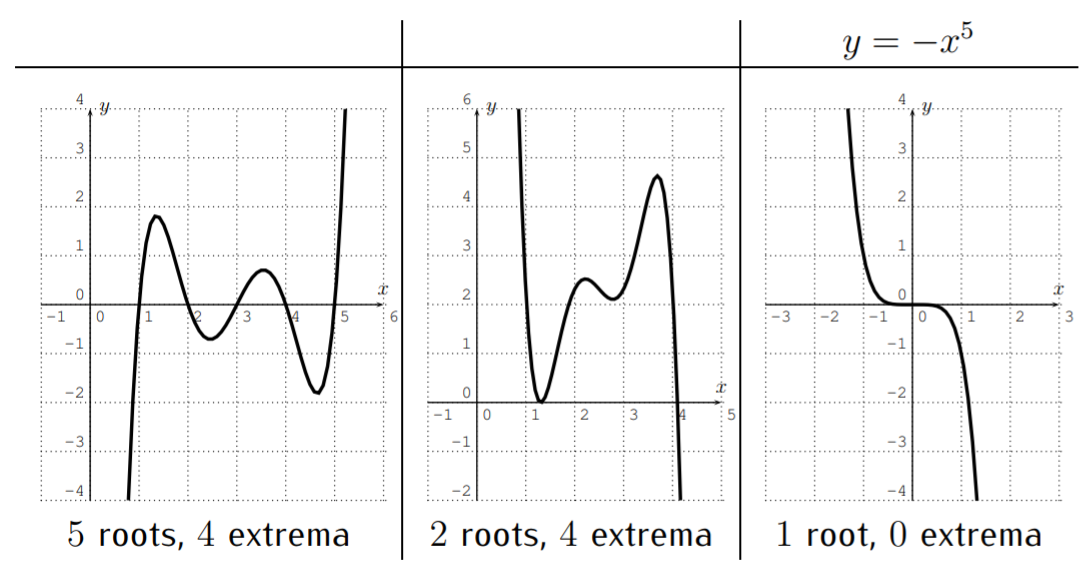
- Dejarf(x)=a_n x^n+a_{n-1} x^{n-1}+\dots +a_2 x^2+ a_1 x + a_0 ser un polinomio de gradon. Entoncesf tiene como máximon raíces, y como muchon-1 extrema.
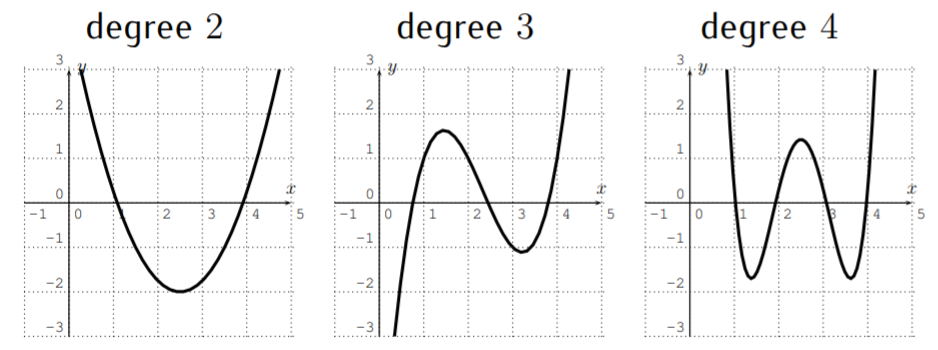
- Asumir que el grado def es parejon=2, 4, 6, \dots. Sia_n>0, entonces el polinomio se abre hacia arriba. Sia_n<0 entonces el polinomio se abre hacia abajo.
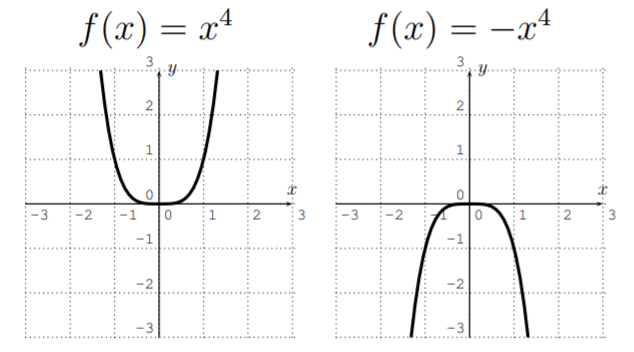
- Supongamos que el grado def es impar,n=1, 3, 5, \dots. Sia_n>0, entonces sef(x) acerca+\infty cuando sex acerca+\infty, yf(x) se acerca-\infty comox enfoques-\infty. Sia_n<0, entonces sef(x) acerca-\infty cuando sex acerca+\infty, yf(x) se acerca+\infty comox enfoques-\infty.
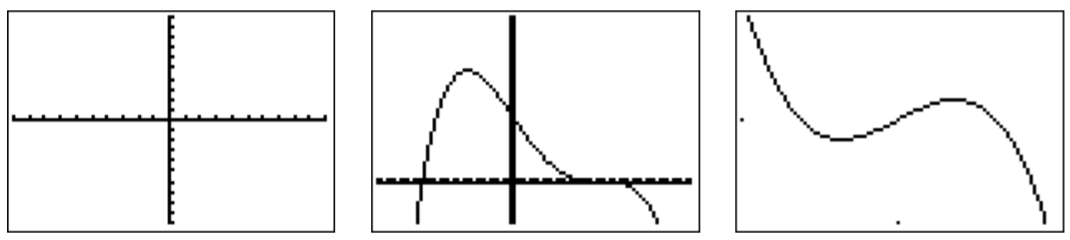
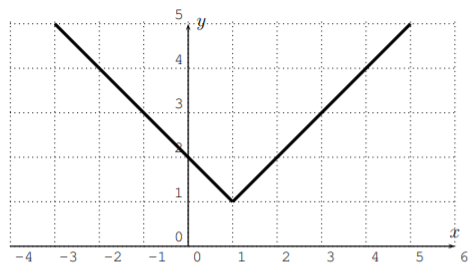
- El dominio de un polinomiof es todo números reales, yf es continuo para todos los números reales (no hay saltos en la gráfica). La gráfica de nof tiene asíntotas horizontales ni verticales, ni discontinuidades (saltos en la gráfica), ni esquinas. Además,f(x) se acerca\pm \infty cuando sex acerca\pm \infty. Por lo tanto, las siguientes gráficas no pueden ser gráficas de polinomios.
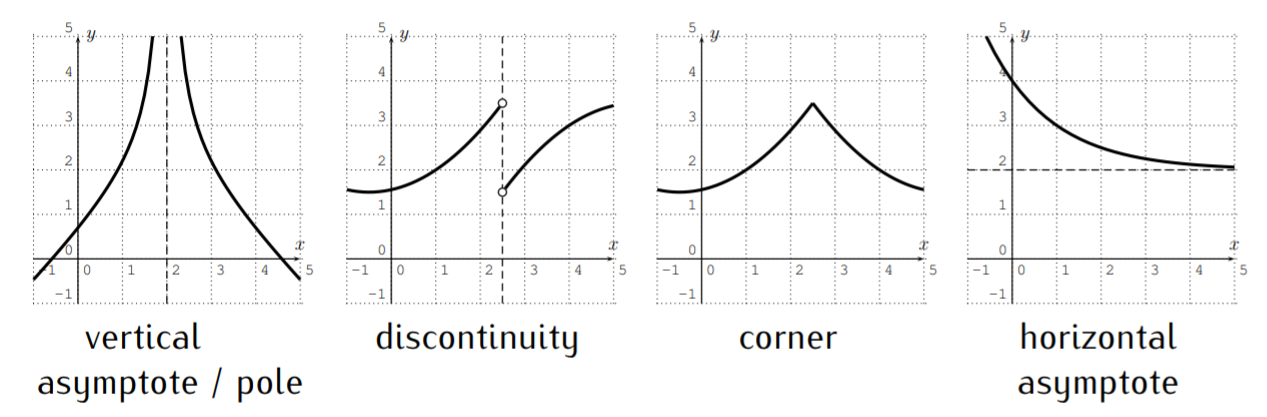
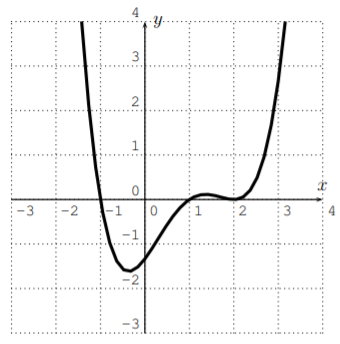
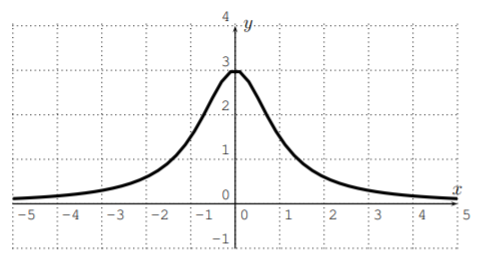
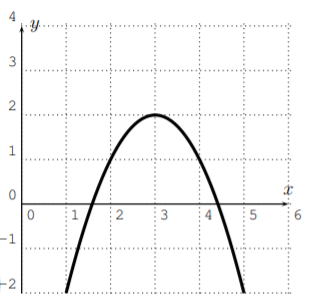
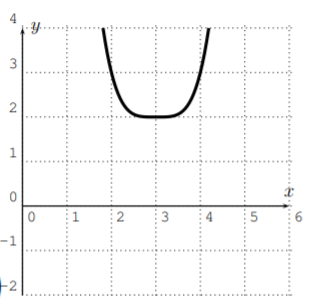
¿Cuáles de las siguientes gráficas podrían ser las gráficas de un polinomio? Si la gráfica pudiera ser efectivamente una gráfica de un polinomio entonces determinar un posible grado del polinomio.
Solución
- Sí, esto podría ser un polinomio. El grado podría ser, por ejemplo,4.
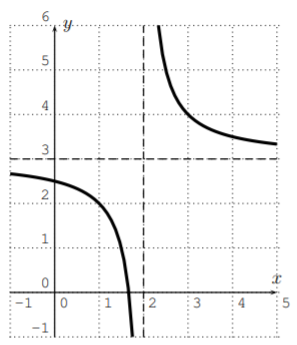
- No, ya que la gráfica tiene un poste.
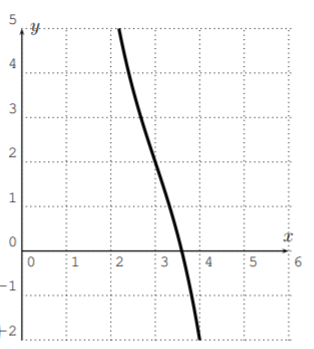
- Sí, esto podría ser un polinomio. Un posible grado sería grado3.
- No, ya que la gráfica tiene una esquina.
- No, ya quef(x) no se acerca\infty ni-\infty comox enfoques\infty. (De hechof(x) se aproxima0 comox enfoques\pm\infty y decimos que la función (o grafo) tiene una asíntota horizontaly=0.)
Identificar las gráficas de los polinomios en (a), (b) y (c) con las funciones (i), (ii) y (iii).
- f(x)=-x^3+9x^2-27x+29
- f(x)=-x^2+6x-7
- f(x)=x^4-12x^3+54x^2-108x+83
Solución
La única función de grado impar es (i) y por lo tanto debe corresponder a la gráfica (c). Para (ii), dado que el coeficiente inicial es negativo, sabemos que la función se abre hacia abajo, de manera que corresponde a la gráfica (a). Finalmente (iii) se abre hacia arriba, ya que el coeficiente principal es positivo, de manera que su gráfica es (b).
Al graficar una función, necesitamos asegurarnos de dibujar la función en una ventana que exprese todas las características interesantes de la gráfica. Más precisamente, debemos asegurarnos de que la gráfica incluya todas las partes esenciales de la gráfica, como todas las intercepciones (tantox -intercepciones comoy -interceptar), todas las raíces, todas las asíntotas (esto se discutirá en la siguiente parte), y el comportamiento a largo plazo de la función (así es como se comporta la función cuando sex acerca\pm \infty). También queremos incluir todos los extremos (es decir, todos los máximos y mínimos) de la función.
Gráfica de la función dada con el TI-84. Incluye todos los extremos e intercepciones de la gráfica en tu ventana de visualización.
- f(x)=-x^3+26x^2-129x+175
- f(x)=.1x^4-2.4x^2+6.4x-35
- f(x)=-5x^3+75x^2-374.998x+630
- f(x)=-.01x^4+.4x^3+.0025x^2-160x+1600
Solución
- El gráfico en la ventana estándar se ve de la siguiente manera:
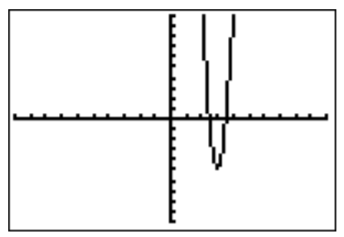
No obstante, dado que la función es de grado3, ésta no puede ser la gráfica completa, comof(x) tiene que acercarse-\infty cuando sex acerca\infty. Alejar el zoom y volver a escalar apropiadamente para la siguiente configuración de la siguiente gráfica.
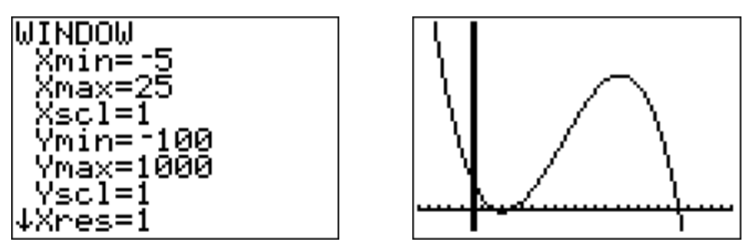
- El gráfico en la ventana estándar se dibuja a la izquierda de abajo. Después de reescalar a-10\leq x\leq 10 y-100 \leq y\leq 30 obtenemos la gráfica de la derecha.
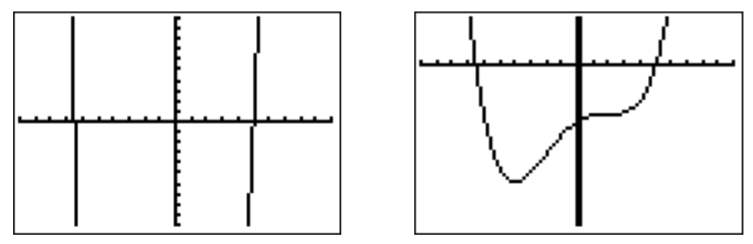
- El gráfico en la ventana estándar se dibuja a la izquierda. Acercando a la parte interesante de la gráfica, obtenemos la gráfica de la derecha. (Abajo, hemos elegido una ventana de4.94\leq x\leq 5.06 y5.00995 \leq y\leq 5.01005.)
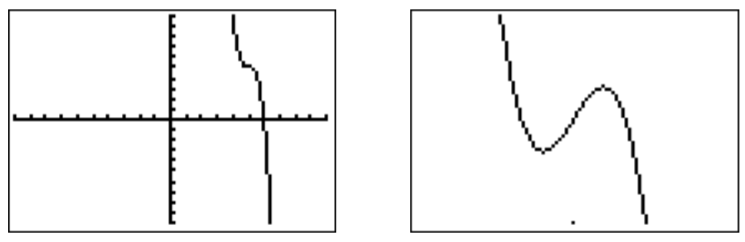
- La ventana estándar (ver gráfica izquierda) muestra un sistema de coordenadas vacío sin ninguna parte de la gráfica. Sin embargo, alejando-30\leq x\leq 40 y-1000 \leq y\leq 4000, obtenemos la gráfica media. Hay otra parte interesante de la gráfica que se muestra a la derecha, proveniente del zoom a la meseta de la derecha (aquí se muestra en19.2\leq x\leq 20.8 y0.9 \leq y\leq 1.1).