9.3: Sección opcional- Graficando polinomios a mano

Última actualización
Guardar como PDF

Page ID: 117654

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección mostraremos cómo esbozar la gráfica de un polinomio factorizado sin el uso de una calculadora.

Ejemplo$\PageIndex{1}$

Dibuje la gráfica del siguiente polinomio sin usar la calculadora:\[p(x)=-2(x+10)^3(x+9)x^2(x-8) \nonumber \]

Solución

Tenga en cuenta que en la calculadora es imposible obtener una ventana que dé todas las características de la gráfica (mientras se enfoca en obtener el máximo a la vista las otras características se vuelven invisibles). Dibujaremos la gráfica a mano para que algunas de las principales características sean visibles. Esto sólo será un boceto y no la gráfica real a escala. Nuevamente, la gráfica no se puede dibujar a escala mientras se pueden ver las características.

Primero comenzamos poniendo las$x$ -intercepciones en la gráfica en el orden correcto, pero no a escala necesariamente. Entonces tenga en cuenta que

\[p(x)=-2x^7+\dots \text{(lower terms)}\quad \approx -2x^7 \quad\quad \text{ for large }|x| \nonumber \]

Este es el término principal del polinomio (si se expande$p$ es el término con mayor potencia) y por lo tanto domina el polinomio para grandes$|x|$. Entonces la gráfica de nuestro polinomio debería parecerse a la gráfica de$y=-2x^7$ en el extremo izquierdo y derecho.

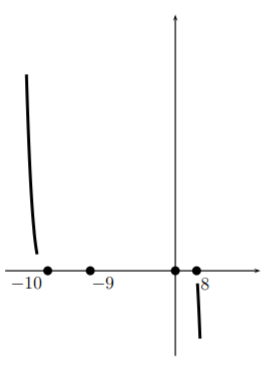
$clipboard_ec9d090155983b6200ca81b18373591b0.png$

Ahora miramos lo que está pasando en las raíces. Cerca de cada raíz domina el factor correspondiente a esa raíz. Así que tenemos

\ [\ begin {array} {r|l|l}
\ texto {para} x\ approx & p (x)\ approx &\
\ hline-10 & C_ {1} (x+10) ^ {3} &\ texto {cúbico}\\
-9 & C_ {2} (x+9) &\ texto {línea}\\
0 & C_ {3} x^ {2} &\ texto {parábola}\\
8 & C_ {4} (x -8) &\ texto {línea}
\ end {array}\ nonumber\]

donde$C_1, C_2, C_3,$ y$C_4$ son constantes que pueden, pero no necesitan, ser calculadas. Por ejemplo, si la parábola cercana$0$ se abre o no hacia arriba o hacia abajo dependerá de si la constante$C_3=-2\cdot (0+10)^3(0+9)(0-8)$ es negativa o positiva. En este caso$C_3$ es positivo por lo que se abre hacia arriba pero no vamos a utilizar este hecho para graficar. Veremos esto independientemente lo cual es una buena comprobación de nuestro trabajo.

Partiendo de la izquierda de nuestra gráfica donde habíamos determinado el comportamiento para grandes negativos$x$, nos movemos hacia la izquierda más cero,$-10$. Cerca de$-10$ la gráfica se ve cúbica por lo que imitamos una curva cúbica a medida que atravesamos$(-10,0)$.

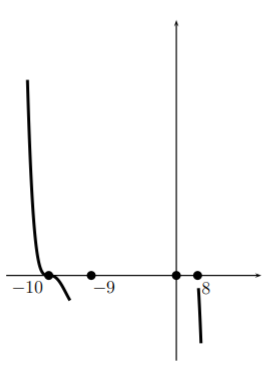
$clipboard_ec2ec7701fee1cc33ae7dfc9cf35a03cc.png$

Ahora giramos y nos dirigimos hacia el siguiente cero,$-9$. Aquí la gráfica se ve como una línea, así que pasamos por el punto$(-9,0)$ como lo haría una línea.

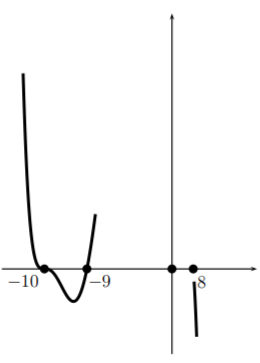
$clipboard_ecb6a6e954ace2a0f14f1a1e4d4f313fc.png$

Ahora giramos y nos dirigimos hacia la raíz$0$. Aquí la gráfica debería verse como una parábola. Entonces ahí formamos una parábola. (Obsérvese que como habíamos dicho antes la parábola debería estar abriéndose hacia arriba aquí —y vemos que lo es).

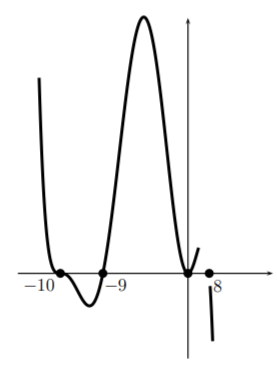
$clipboard_e32117a3e27cf9eeb55d8423ece3ad4b8.png$

Ahora giramos hacia el cero final$8$. Pasamos por el punto$(8,0)$ como una línea y nos unimos (quizás con el uso de una goma de borrar) a la gran$x$ parte de la gráfica. Si esto no se une muy bien (si la gráfica va en la dirección equivocada) entonces ha habido un error. Esto es un chequeo de tu trabajo. Aquí está el boceto final.

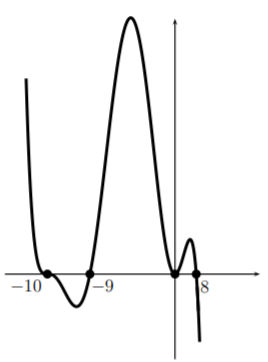
$clipboard_e2222c59a132862518c5e8f758c3b160d.png$

¿Qué se puede entender de este boceto? Preguntas como '¿cuándo es$p(x)>0$?' se puede responder mirando el boceto. Además, la forma general de la curva es correcta por lo que se pueden concluir otras propiedades. Por ejemplo,$p$ tiene un mínimo local entre$x=-10$ y$x=-9$ y un máximo local entre$x=-9$ y$x=0$, y entre$x=0$ y$x=8$. El punto exacto donde la función alcanza su máximo o mínimo no se puede decidir mirando este boceto. Pero ayudará a decidir sobre una ventana adecuada para que se pueda utilizar el buscador mínimo o máximo en la calculadora.