9.2: Hallar raíces de un polinomio con el TI-84

Última actualización
Guardar como PDF

Page ID: 117653

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos visto que las raíces son características importantes de un polinomio. Recordemos que las raíces del polinomio$f$ son aquellas$x_0$ para las cuales$f(x_0)=0$. Estas son, por supuesto, precisamente las$x$ -intercepciones de la gráfica. Por lo tanto, podemos usar la gráfica de un polinomio para encontrar sus raíces como lo hicimos en la sección 9.1.

Ejemplo$\PageIndex{1}$

Encuentra las raíces del polinomio a partir de su gráfica.

$f(x)=x^3-7x^2+14x-8$
$f(x)=-x^3+8x^2-21x+18$
$f(x)=x^4+3x^3-x+6$
$f(x)=x^5-3x^4-8x^3+24x^2+15x-45$

Solución

Comenzamos por graficar el polinomio$f(x)=x^3-7x^2+14x-8$.

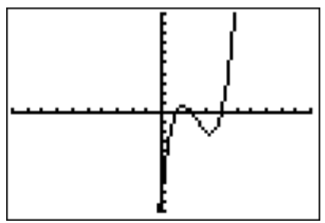
$clipboard_edcb949527590ff5952fe3b0ae602d419.png$

La gráfica sugiere que las raíces están en$x=1$,$x=2$, y$x=4$. Esto se puede verificar fácilmente mirando la tabla de funciones.

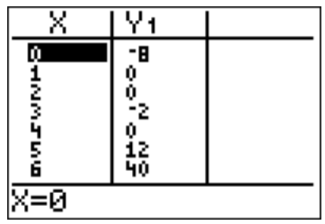
$clipboard_e6da3a5d8ec9640277dd5b4c9d6879a8e.png$

Dado que el polinomio es de grado$3$, no puede haber otras raíces.

Graficando$f(x)=-x^3+8x^2-21x+18$ con la calculadora muestra la siguiente pantalla.

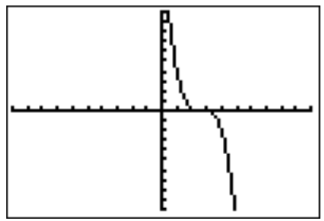
$clipboard_eae2416f224e9958caa45bbb7e50f9e18.png$

Al hacer zoom en la gráfica se revela que de hecho hay dos raíces,$x=2$ y$x=3$, lo que se puede confirmar a partir de la tabla.

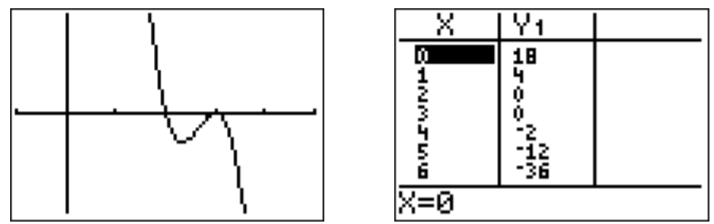
$clipboard_e1947d600a72bca5e2acfdf0dcf423ad5.png$

Tenga en cuenta, que la raíz$x=3$ sólo “toca” el$x$ eje -eje. Esto se debe a que$x=3$ aparece como una raíz múltiple. En efecto, como$3$ es una raíz, podemos dividir$f(x)$ por$x-3$ sin resto y factificar el cociente resultante para ver que eso

\[f(x)=(x-2)(x-3)(x-3)=(x-2)(x-3)^2 \nonumber \]

Decimos que$x=3$ es una raíz de multiplicidad$2$.

El gráfico de$f(x)=x^4+3x^3-x+6$ en la ventana estándar se muestra de la siguiente manera.

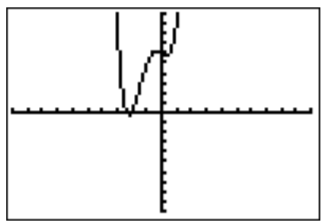
$clipboard_ed59e5c6a0df672efd21e9150ca2ef4d9.png$

Dado que se trata de un polinomio de grado$4$, todas las características esenciales ya se muestran en la gráfica anterior. Las raíces se pueden ver haciendo zoom en la gráfica.

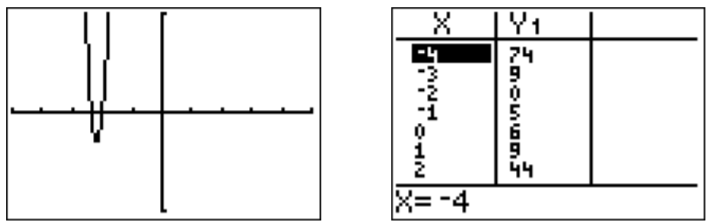
$clipboard_ebeebee66979937e3174d9ada597fa63f.png$

De la tabla y la gráfica vemos que hay una raíz en$x=-2$ y otra raíz en el medio$-3$ y$-2$. Encontrar el valor exacto de esta segunda raíz puede ser bastante difícil, y diremos más sobre esto en la sección 2 a continuación. En este punto, solo podemos aproximar la raíz con la función “cero” desde el menú “calc”:

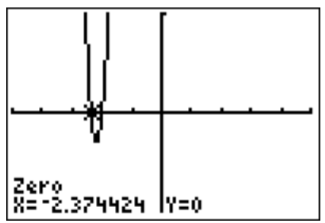
$clipboard_e479499fb2df2748ad37424c393bd6f3b.png$

El gráfico de$f(x)=x^5-3x^4-8x^3+24x^2+15x-45$ en la ventana estándar se muestra a continuación.

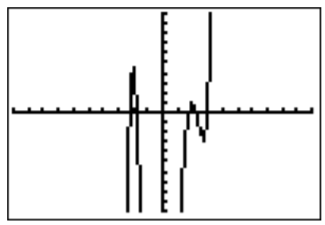
$clipboard_e19f8fa676e4280cdb49848d62e0bc603.png$

Al hacer zoom en el$x$ eje -y verificar la tabla se muestra que la única raíz obvia es$x=3$.

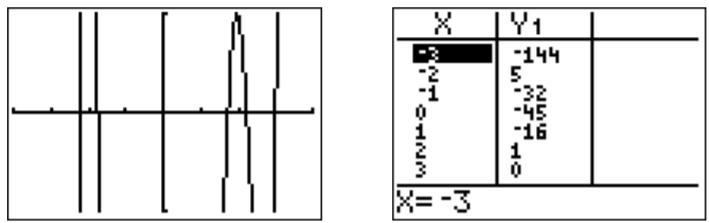
$clipboard_e4b44da67050ee8514d72bcd6a4d5256b.png$

Las otras cuatro raíces son más difíciles de encontrar. Sin embargo, se pueden aproximar usando la función “cero” del menú “calc”.

A menudo será necesario encontrar las raíces de un polinomio cuadrático. Por ello, recordamos la conocida fórmula cuadrática.

Teorema: Fórmula Cuadrática

Las soluciones de la ecuación$f(x)=ax^2+bx+c$ para algunos números reales$a$,$b$, y$c$ están dadas por:

\[x_{1}=\dfrac{-b+\sqrt{b^{2}-4 a c}}{2 a}, \quad \text { and } \quad x_{2}=\dfrac{-b-\sqrt{b^{2}-4 a c}}{2 a} \nonumber \]

Podemos combinar las dos soluciones$x_1$$x_2$ y simplemente escribir esto como:

\[\boxed{x_{1 / 2}=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}} \nonumber \]

Nota

Siempre podemos usar las raíces$x_1$ y$x_2$ de un polinomio cuadrático$f(x)=ax^2+bx+c$ de la fórmula cuadrática y reescribir el polinomio como:

\[\boxed{f(x)=a x^{2}+b x+c=a \cdot\left(x-\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}\right)\left(x-\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}\right)} \nonumber \]

Ejemplo\(\PageIndex{1}\)

Teorema: Fórmula Cuadrática

Nota