10.1: Sección opcional- El teorema de la raíz racional
- Page ID
- 117710
Considera la ecuación\(10x^3-6x^2+5x-3=0\). \(x\)Sea una solución racional de esta ecuación,\(x=\dfrac p q\) es decir, un número racional tal que
\[10\cdot\Big(\dfrac p q\Big)^3-6\cdot\Big(\dfrac p q\Big)^2+5\cdot\dfrac p q-3=0 \nonumber \]
Suponemos que\(x=\dfrac p q\) está completamente reducido, es decir,\(p\) y no\(q\) tenemos factores comunes que puedan utilizarse para cancelar el numerador y denominador de la fracción\(\dfrac p q\). Ahora, simplificando la ecuación anterior, y combinando términos, obtenemos:
\[\begin{aligned} && 10\cdot\dfrac {p^3} {q^3}-6\cdot\dfrac {p^2} {q^2}+5\cdot\dfrac p q-3 = 0\\ \text{(multiply by $q^3$)} &\implies & 10 p^3-6p^2q+5pq^2-3q^3 =0\\ \text{(add $3q^3$)} &\implies & 10 p^3-6p^2q+5pq^2=3q^3 \\ \text{(factor $p$ on the left)} &\implies & p\cdot(10 p^2-6pq+5q^2)=3q^3 \end{aligned} \nonumber \]
Por lo tanto,\(p\) es un factor de\(3q^3\) (siendo el otro factor\((10 p^2-6pq+5q^2)\)). Ya que\(p\) y no\(q\) tienen factores comunes,\(p\) debe ser un factor de\(3\). Es decir,\(p\) es uno de los siguientes enteros:\(p=+1, +3, -1, -3\)
Del mismo modo a partir de\(10 p^3-6p^2q+5pq^2-3q^3 =0\), podemos escribir
\[\begin{aligned} \text{(add $+6p^2q-5pq^2+3q^3 $)} &\implies & 10 p^3=6p^2q-5pq^2+3q^3 \\ \text{(factor $q$ on the right)} &\implies & 10 p^3=(6p^2-5pq+3q^2)\cdot q \end{aligned}\]
Ahora,\(q\) debe ser un factor de\(10p^3\). Ya que\(q\) y no\(p\) tienen factores comunes,\(q\) debe ser un factor de\(10\). En otras palabras,\(q\) es uno de los siguientes números:\(q=\pm1, \pm 2, \pm 5, \pm 10\). Armando esto con las posibilidades para\(p=\pm 1, \pm 3\), vemos que todas las raíces racionales posibles son las siguientes:
\[\pm\dfrac{1}{1},\quad \pm\dfrac{1}{2},\quad \pm\dfrac{1}{5},\quad \pm\dfrac{1}{10},\quad \pm\dfrac{3}{1},\quad \pm\dfrac{3}{2},\quad \pm\dfrac{3}{5},\quad \pm\dfrac{3}{10} \nonumber \]
La observación en el ejemplo anterior se mantiene para una ecuación polinómica general con coeficientes enteros.
Considera la ecuación\[a_n x^n+a_{n-1}x^{n-1}+\dots + a_1 x + a_0=0 \label{EQnthorder} \]
donde cada coeficiente\(a_n, a_{n-1},\dots, a_0\) es un número entero y\(a_0\neq 0\),\(a_n\neq 0\). Supongamos que\(x=\dfrac p q\) es una solución de\(\ref {EQnthorder}\) y la fracción\(x=\dfrac p q\) se reduce por completo. Entonces\(a_0\) es un múltiplo entero de\(p\), y\(a_n\) es un múltiplo entero de\(q\).
Por lo tanto, todas las posibles soluciones racionales de\(\ref {EQnthorder}\) son fracciones\(x=\dfrac p q\) donde\(p\) es un factor de\(a_0\) y\(q\) es un factor de\(a_n\).
Podemos usar esta observación para encontrar buenos candidatos para las raíces de un polinomio dado.
- Encuentra todas las raíces racionales de\(f(x)=7x^3+x^2+7x+1\).
- Encuentra todas las raíces reales de\(f(x)=2x^3+11x^2-2x-2\).
- Encuentra todas las raíces reales de\(f(x)=4x^4-23x^3-2x^2-23x-6\).
Solución
- Si\(x=\dfrac p q\) es una raíz racional, entonces\(p\) es un factor de\(1\), es decir\(p=\pm1\), y\(q\) es un factor de\(7\), es decir\(q=\pm 1, \pm 7\). Por lo tanto, los candidatos a las raíces racionales son\(x=\pm \dfrac 1 1, \pm \dfrac 1 7\). Para ver cuáles de estos candidatos son efectivamente raíces de\(f\) conectamos estos números a\(f\) través de la calculadora. Obtenemos lo siguiente:
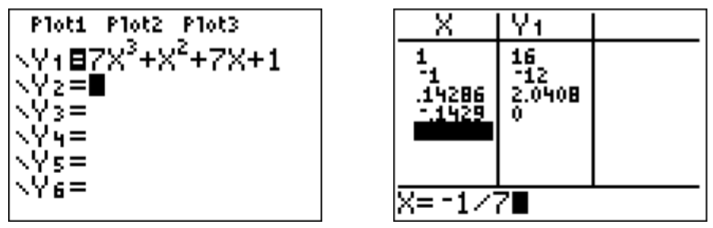
Tenga en cuenta que ingresamos el\(x\) -valor como una fracción “\((-)1/7\)” a la derecha. La única raíz entre\(\pm 1, \pm \dfrac 1 7\) es\(x=-\dfrac 1 7\).
- Necesitamos identificar todas las raíces reales de\(f(x)=2x^3+11x^2-2x-2\). En general, es una tarea bastante difícil encontrar una raíz de un polinomio de grado\(3\), de manera que será útil si podemos encontrar primero las raíces racionales. Si\(x=\dfrac p q\) es una raíz racional entonces\(p\) es un factor de\(-2\), es decir\(p=\pm 1, \pm 2\), y\(q\) es un factor de\(2\), es decir\(q=\pm 1, \pm 2\). Las posibles raíces racionales\(x=\dfrac p q\) de\(f\) son:\[\pm 1, \quad \pm 2, \quad \pm \dfrac 1 2 \nonumber \] Usando la calculadora, vemos que la única raíz racional es\(x=\dfrac 1 2\).
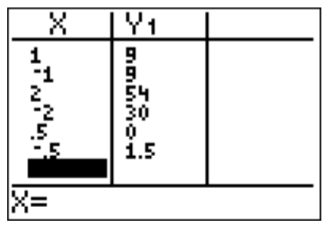
Por lo tanto, por el teorema factorial (Observación Resto), vemos que\(\left (x-\dfrac 1 2 \right )\) es un factor de\(f\), es decir\(f(x)=q(x)\cdot \left (x-\dfrac 1 2 \right )\). Para evitar fracciones en la división larga, reescribimos esto\[f(x)=q(x)\cdot \left (x-\dfrac 1 2 \right )=q(x)\cdot \dfrac{2x-1}{2}=\dfrac{q(x)}2 \cdot(2x-1) \nonumber \] para que podamos dividir\(f(x)\) por\((2x-1)\) en lugar de\(\left (x-\dfrac 1 2 \right )\) (tenga en cuenta que esto no se puede hacer con división sintética). Obtenemos el siguiente cociente.
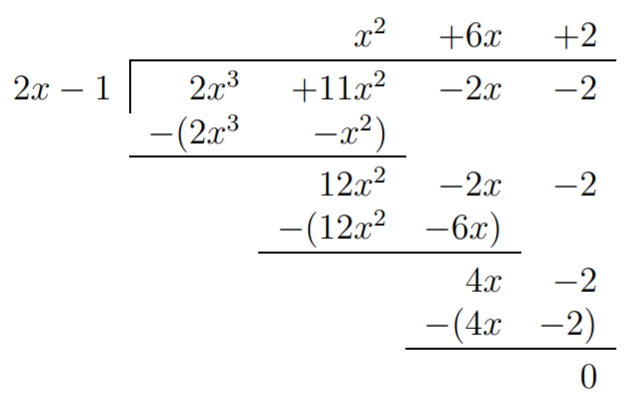
Por lo tanto\(f(x)=(x^2+6x+2)(2x-1)\),, y cualquier raíz de\(f\) es una raíz de\(x^2+6x+2\) o de\(2x-1\). Sabemos que la raíz de\(2x-1\) es\(x=\dfrac 1 2\), y eso no\(x^2+6x+2\) tiene otras raíces racionales. Sin embargo, podemos identificar todas las demás raíces reales de\(x^2+6x+2\) vía la fórmula cuadrática, (ver Teorema para la Fórmula Cuadrática).
\[\begin{aligned} x^2+6x+2=0 \quad \implies \quad x_{1/2} & = & \dfrac{-6\pm\sqrt{6^2-4\cdot 1\cdot 2}}{2}\\ &=& \dfrac{-6\pm\sqrt{36-8}}{2}=\dfrac{-6\pm\sqrt{28}}{2}\\ &=& \dfrac{-6\pm\sqrt{4\cdot 7}}{2}=\dfrac{-6\pm2\sqrt{7}}{2}\\ &=& -3\pm\sqrt{7}\end{aligned} \nonumber \]
Por lo tanto, las raíces de\(f\) son precisamente las siguientes\[x_1=-3+\sqrt{7}, \quad x_2=-3-\sqrt{7}, \quad x_3=\dfrac 1 2 \nonumber \]
- Primero encontramos las raíces racionales\(x=\dfrac p q\) de\(f(x)=4x^4-23x^3-2x^2-23x-6\). Ya que\(p\) es un factor de\(-6\) ello debe ser\(p=\pm 1, \pm 2, \pm 3, \pm 6\), y ya que\(q\) es un factor de\(4\) ello debe ser\(q=\pm 1, \pm 2, \pm 4\). Todos los candidatos a las raíces racionales\(x=\dfrac p q\) son los siguientes (donde excluimos las formas repetidas de escritura\(x\)):\[\pm 1,\quad \pm 2,\quad \pm 3,\quad \pm 6,\quad \pm \dfrac 1 2,\quad \pm \dfrac 3 2,\quad \pm \dfrac 1 4,\quad \pm \dfrac 3 4 \nonumber \] Comprobando a todos estos candidatos con la calculadora produce exactamente dos raíces racionales:\(x=6\) y\(x=-\dfrac 1 4\). Por lo tanto, podemos dividir\(f(x)\) por ambos\((x-6)\) y por\(\left(x+\dfrac 1 4 \right)\) sin resto. Para evitar fracciones, usamos el término\(4\cdot \left(x+\dfrac 1 4 \right)=(4x+1)\) en lugar de\(\left(x+\dfrac 1 4 \right)\) para nuestro factor de\(f\). Por lo tanto,\(f(x)=q(x)\cdot (x-6)\cdot (4x+1)\). El cociente\(q(x)\) se determina realizando una división larga por\((x-6)\) y luego otra división larga por\((4x+1)\), o alternativamente por solo una división larga\[(x-6)\cdot (4x+1)=4x^2+x-24x-6=4x^2-23x-6 \nonumber \] Dividiendo\(f(x)=4x^4-23x^3-2x^2-23x-6\) por\(4x^2-23x-6\) produce el cociente\(q(x)\):
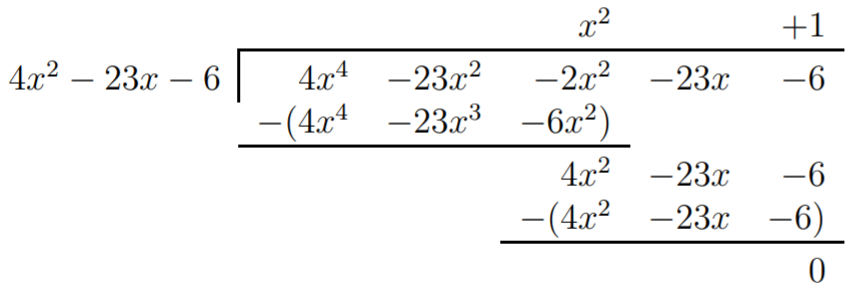
Obtenemos la expresión factorizada para\(f(x)\) as\(f(x)= (x^2+1)(4x+1)(x-6)\). Las únicas raíces reales que nos quedan son las de\(x^2+1\). Sin embargo, no\[x^2+1=0 \quad\implies \quad x^2=-1 \nonumber \] tiene una solución real. En otras palabras, solo hay soluciones complejas de\(x^2=-1\), que son\(x=i\) y\(x=-i\) (discutiremos soluciones complejas con más detalle en la siguiente sección). Dado que el problema requiere que encontremos las raíces reales de\(f\), nuestra respuesta es que las únicas raíces reales son\(x_1=6\) y\(x_2=-\dfrac 1 4\).