10.2: El teorema fundamental del álgebra
- Page ID
- 117709
Hemos visto en Observación (Resto) que cada raíz\(c\) de un polinomio\(f(x)\) da un factor\((x-c)\) de\(f(x)\). Hay un teorema que dice algo sobre la existencia de raíces y factores pero tendremos que discutir brevemente los números complejos antes de afirmar ese teorema.
Como se indicó anteriormente, sabemos que no hay un número real que satisfaga\(x^2=-1\). Entonces\(i\) definimos como una solución a esta ecuación. Este no\(i\) es un número real sino un nuevo tipo de número llamado número complejo. Podemos pensar en\(i\) como\(\sqrt{-1}\). Ahora podemos considerar números de la forma\(a+ib\) donde\(a\) y\(b\) son números reales. Los números de esta forma constituye el conjunto de números complejos, denotados por\(\mathbb{C}\). \(a\)se llama la parte real y\(b\) se llama la parte imaginaria del número complejo\(a+i b\). Podemos sumar dos números complejos sumando sus partes real e imaginaria para formar las partes real e imaginaria de la suma. Podemos multiplicar dos números complejos por distribución ordinaria (FOIL) luego usar la propiedad que\(i^2=-1\).
Tenemos
\[(2-3i)-(4+3i)=(2-4)+(-3-3)i=-2-6i \nonumber \]
y
\[(2-3i)(4+3i)=8+6i-12i-9i^2=8-6i-9(-1)=17-6i \nonumber \]
Podemos ver escribiendo, por ejemplo,\(\sqrt{-6}=i\sqrt{6}\), que estos números surgen naturalmente como raíces de ecuaciones cuadráticas. ¡Pero hay más! El siguiente teorema fundamental del álgebra garantiza la existencia de raíces de cualquier polinomio.
Dejar\(f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}\), ser un polinomio no constante. Entonces existe un número complejo\(c\) que es una raíz de\(f\).
Hagamos dos observaciones sobre el teorema fundamental del álgebra para aclarar la afirmación del teorema.
- En el Teorema anterior no especificamos qué tipo de coeficientes\(a_0,\dots a_n\) se permiten para que el teorema mantenga. De hecho, para ser precisos, el teorema fundamental del álgebra establece que para cualquier número complejo\(a_0,\dots a_n\), el polinomio\(f(x)=a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) tiene una raíz.
- En general puede que no exista una raíz real\(c\) de un polinomio dado, pero la raíz sólo\(c\) puede ser un número complejo. Por ejemplo, considerar\(f(x)=x^2+1\), y considerar las raíces\(c\) de\(f\), es decir\(c^2+1=0\). Entonces, para cualquier número real\(c\), siempre lo hemos hecho\(c^2\geq 0\), así que\(f(c)=c^2+1\geq 1\), para que no pueda haber una raíz real\(c\) de\(f\). No obstante, si nos\[(x-i)(x+i)=x^2+xi-xi-i^2=x^2+1 \nonumber \] multiplicamos vemos que\(f\) tiene raíces complejas\(c=i\) y\(c=-i\).
Ahora bien, mientras que el teorema fundamental del álgebra garantiza una raíz\(c\) de un polinomio\(f\), podemos usar el teorema restante de Observación (Resto) para verificar posibles candidatos\(c\) para las raíces, y el teorema de factor a factor \(f(x)=q(x)\cdot (x-c)\).
Encontrar raíces del polinomio dado y utilizar esta información para factorizar el polinomio por completo.
- \(f(x)=2x^3-8x^2-6x+36\)
- \(f(x)=x^4-3x^3-36x^2+68x+240\)
- \(f(x)=x^3+1\)
- \(f(x)=x^4-16\)
Solución
- Para encontrar una raíz, utilizamos la gráfica para hacer una conjetura para una de las raíces.
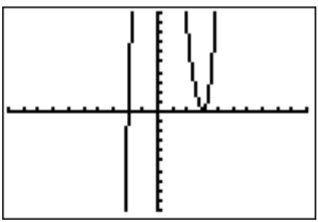
La gráfica sugiere que las raíces pueden estar en\(x=-2\) y\(x=3\). Esto también se apoya al mirar la tabla para la función.
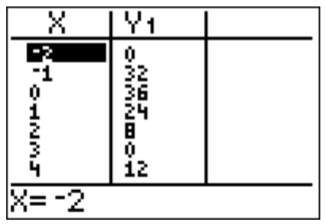
Comprobamos que estas son raíces al enchufar los números a la función.
\[\begin{aligned} f(-2)&= 2\cdot (-2)^3-8\cdot (-2)^2-6\cdot (-2)+36=-16-32+12+36=0\\ f(3)&= 2\cdot 3^3-8\cdot 3^2-6\cdot 3+36=54-72-18+36=0\end{aligned} \nonumber \]
Por el teorema factorial podemos dividir\(f(x)=2x^3-8x^2-6x+36\), por ejemplo, por\((x-3)\).
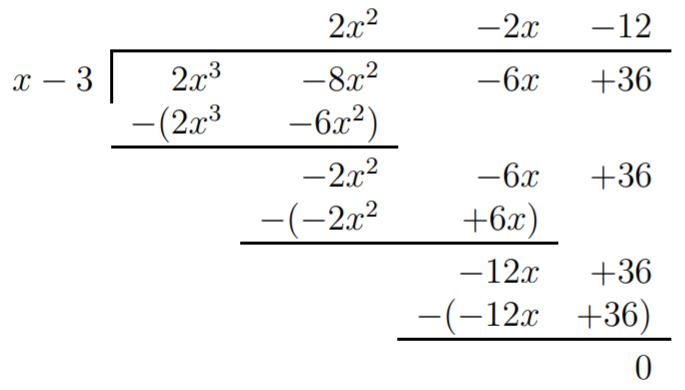
Por lo tanto,\(f(x)=(2x^2-2x-12)(x-3)\). Para factorizar\(f\) completamente, todavía necesitamos factorizar el primer polinomio\(2x^2-2x-12\):
\[\begin{aligned} f(x)&=(2x^2-2x-12)(x-3)\\ &=2\cdot(x^2-x-6)\cdot (x-3)\\ &= 2\cdot (x-3)\cdot(x+2)\cdot (x-3)\\ &=2\cdot (x+2)\cdot (x-3)^2 \end{aligned} \nonumber \]
- La gráfica de\(f(x)=x^4-3x^3-36x^2+68x+240\) en la ventana estándar es la siguiente:
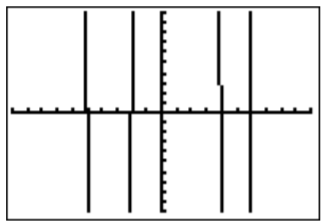
Sospechamos que\(x=-5\)\(x=-2\),\(x=4\),, y\(x=6\) son las raíces de la función. Esto se confirma comprobando la tabla en la calculadora, y también por cómputo directo.
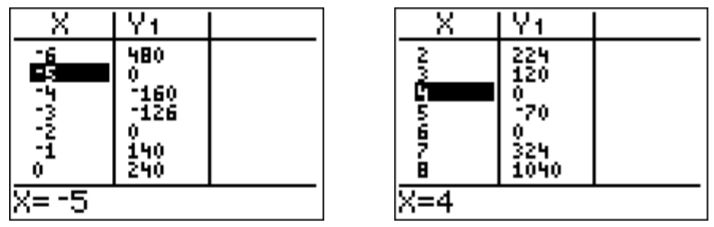
\[\begin{aligned} f(-5)&=(-5)^4-3(-5)^3-36(-5)^2+68(-5)+240 =0\\ f(-2)&=(-2)^4-3(-2)^3-36(-2)^2+68(-2)+240 =0\\ f(4)&=4^4-3\cdot 4^3-36\cdot 4^2+68\cdot 4+240 =0\\ f(6)&=6^4-3\cdot 6^3-36\cdot 6^2+68\cdot 6+240 =0\end{aligned} \nonumber \]
Por lo tanto\((x+5)\), cada\((x+2)\)\((x-4)\),, y\((x-6)\) es un factor de\(f(x)\), y entonces su producto también es un factor de\(f(x)\). El producto\((x+5)(x+2)(x-4)(x-6)\) se calcula de la siguiente manera. Desde\((x+5)(x+2)=x^2+7x+10\) y\((x-4)(x-6)=x^2-10x+24\), obtenemos
\[\begin{aligned} (x+5)(x+2)(x-4)(x-6) &= ({\color{Red} {x^2}}+{\color{Blue} {7x}}+{\color{Green} {10}})(x^2-10x+24) \\ &={\color{Red} {x^4-10x^3+24x^2}}{\color{Blue} {+7x^3-70x^2+168x}}{\color{Green} {+10x^2-100x+240}} \\ &=x^4-3x^3-36x^2+68x+240\\ &=f(x)\end{aligned} \nonumber \]
Vemos que esto es precisamente\(f(x)\), para que no sea necesaria más división polinómica. La respuesta es\(f(x)=(x+5)(x+2)(x-4)(x-6)\).
- Podemos graficar la función, o simplemente hacer una conjetura para una raíz de\(f(x)=x^3+1\). Una conjetura inmediata sería intentarlo\(x=-1\). Esto es efectivamente una raíz, ya que\(f(-1)=(-1)^3+1=-1+1=0\), que también es compatible con la gráfica.
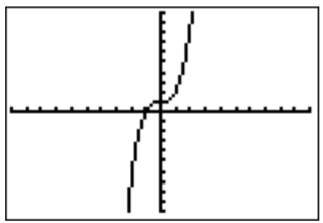
Por lo tanto, podemos dividirnos\(x^3+1\) por\(x+1\).
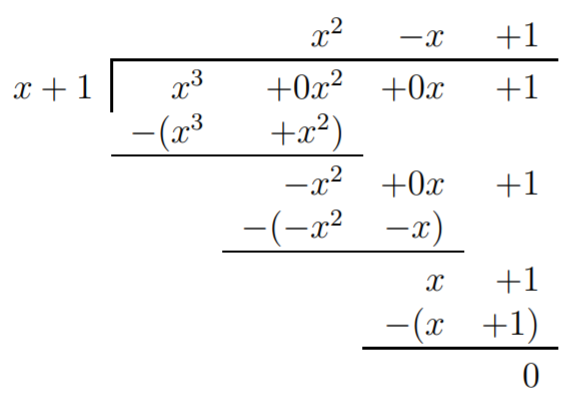
Obtenemos\(f(x)=x^3+1=(x^2-x+1)(x+1)\). Ahora\(x+1\) no se puede factorizar más, sin embargo, podemos seguir factorizando\(x^2-x+1=(x-x_1)(x-x_2)\). Utilizando la fórmula cuadrática, obtenemos las soluciones de\(x^2-x+1=0\) como
\[x_{1/2}=\dfrac{-(-1)\pm\sqrt{(-1)^2-4\cdot 1\cdot 1}}{2\cdot 1}=\dfrac{1\pm\sqrt{-3}}{2} =\dfrac 1 2 \pm i \dfrac{\sqrt{3}}{2} \nonumber \]
Por lo tanto,\(x^3+1=\left (x-\left (\dfrac 1 2 + i\dfrac{\sqrt{3}}{2} \right ) \right )\cdot \left (x- \left (\dfrac 1 2 - i\dfrac{\sqrt{3}}{2} \right ) \right )\cdot (x+1)\).
- Porque\(f(x)=x^4-16\) ahí están los dos candidatos obvios\(x=2\) y\(x=-2\) que podemos identificar como raíces, ya sea adivinando (desde\(2^4=16\)) o mirando la gráfica.
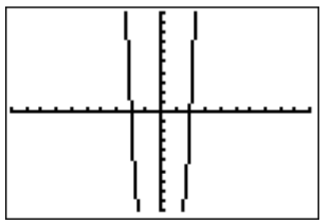
Efectivamente el álgebra confirma estas conjeturas.
\[\begin{aligned} f(2)&= 2^4-16=16-16=0\\ f(-2)&= (-2)^4-16=16-16=0\end{aligned} \nonumber \]
Por lo tanto,\(f(x)=q(x)\cdot (x-2)\cdot (x+2)=q(x)\cdot (x^2-4)\). Para encontrar\(q(x)\) realizamos la división larga\((x^4-16)/(x^2-4)\).
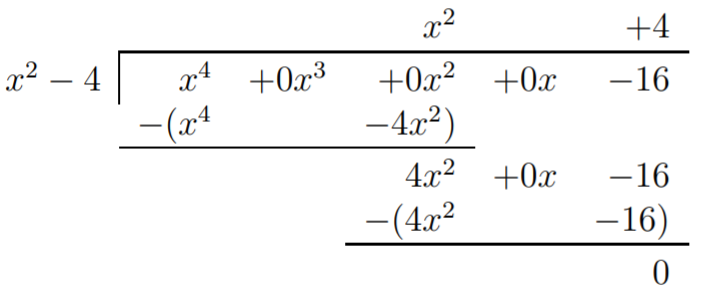
Obtenemos\(f(x)=(x^2+4)(x+2)(x-2)\). Las raíces de\(x^2+4\) están dadas por la fórmula cuadrática como
\[x_{1/2}=\dfrac{-0\pm\sqrt{0^2-4\cdot 1\cdot 4}}{2\cdot 1}=\pm\dfrac{\sqrt{-16}}{2}=\pm\dfrac{4i}{2}=\pm 2i \nonumber \]
o alternativamente,\(x^2+4=0\implies x^2=-4\implies x=\pm 2i\). Obtenemos el polinomio factorizado\(f(x)=(x+2i)(x-2i)(x+2)(x-2)\).
Como hemos visto en el último ejemplo, podemos utilizar las raíces para factorizar un polinomio completamente de manera que todos los factores sean polinomios de grado\(1\) solamente. Además, siempre que una raíz compleja\(a+ib\), aparecía, su conjugada\(a-ib\), también era una raíz. Estas observaciones se mantienen de manera más general, como señalamos ahora.
- Cada polinomio\(f(x)=a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) de grado\(n\) puede ser factorizado como\[f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot \dots \cdot (x-c_n) \nonumber \]
- En particular, cada polinomio de grado\(n\) tiene como máximo\(n\) raíces. (Sin embargo, estas raíces pueden ser reales o complejas).
- El factor\((x-c)\) para una raíz\(c\) podría aparecer varias veces en el producto anterior, es decir, podemos tener\((x-c)^k\) como factor de\(f\). La multiplicidad de una raíz\(c\) es el número de veces\(k\) que aparece una raíz en la expresión factorizada para\(f\) como en (1).
- Si solo\(f(x)=a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0\) tiene coeficientes reales\(a_0,\dots, a_n\), y\(c=a+bi\) es una raíz compleja de\(f\), entonces el conjugado complejo también\(\bar c=a-bi\) es una raíz de\(f\).
- Prueba: Si\(x\) hay alguna raíz, entonces\(a_n x^n+a_{n-1}x^{n-1}+\dots+a_1 x+a_0=0\). Aplicando el complejo conjugado a esto y usando eso\(\overline{u\cdot v}=\bar u \cdot \bar v\) da\(\overline{a_n} \bar{x}^n+\overline{a_{n-1}}\bar{x}^{n-1}+\dots+\overline{a_1} \bar x+\overline{a_0}=0\). Ya que los coeficientes\(a_j\) son reales, tenemos eso\(\overline{a_j}=a_j\), así que eso\(a_n \bar x^n+a_{n-1}\bar x^{n-1}+\dots+a_1 \bar x+a_0=0\). Esto demuestra que el conjugado complejo también\(\bar x\) es una\(f\) raíz de.
Encuentra las raíces del polinomio y dibuja su gráfica incluyendo todas las raíces.
- \(f(x)=x^3+2x^2-14x-3\)
- \(f(x)=x^4-7x^3+11x^2-7x+10\)
Solución
- Para encontrar una raíz, primero graficamos la función\(f(x)=x^3+2x^2-14x-3\) con la calculadora. La gráfica y la tabla sugieren que tenemos una raíz en\(x=3\).
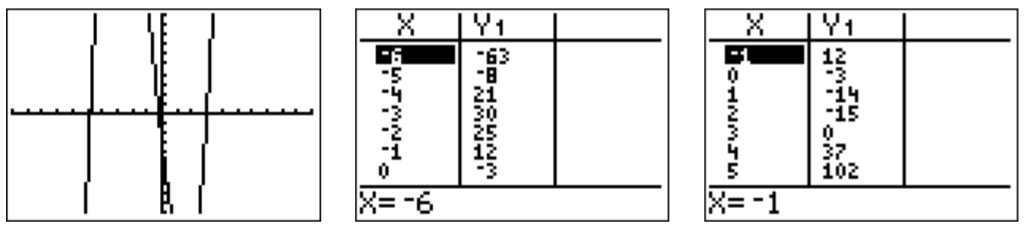
Por lo tanto dividimos\(f(x)\) por\((x-3)\). Obtenemos:
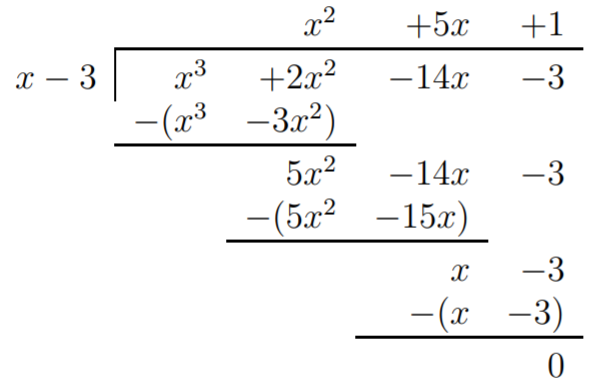
Esto demuestra que\(f(x)=(x-3)(x^2+5x+1)\). Para encontrar las raíces de\(f\), también tenemos que encontrar las raíces del segundo factor\(x^2+5x+1\), es decir, las soluciones a\(x^2+5x+1=0\). La fórmula cuadrática da:
\[x=\dfrac{-5\pm\sqrt{5^2-4\cdot 1 \cdot 1}}{2\cdot 1}=\cfrac{-5\pm\sqrt{21}}{2} \nonumber \]
Por lo tanto, las raíces son:
\[x=3, \quad\quad x=\dfrac{-5+\sqrt{21}}{2}\approx -0.2, \quad\quad x=\dfrac{-5-\sqrt{21}}{2}\approx -4.8 \nonumber \]
Juntamos estas raíces con la gráfica en una ventana apropiada.
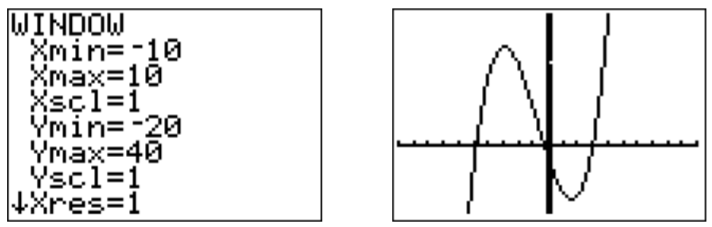
La gráfica que incluye las raíces se muestra a continuación.
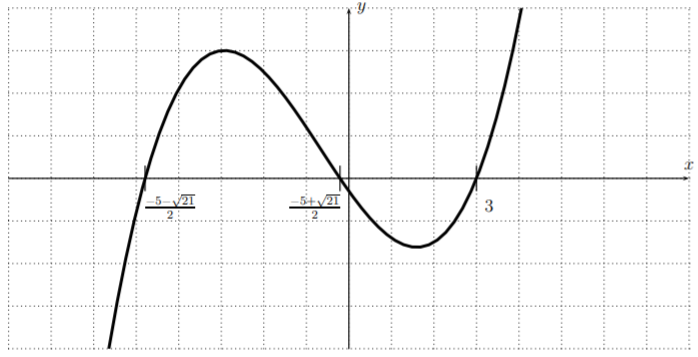
- La gráfica de\(f(x)=x^4-7x^3+11x^2-7x+10\) en una ventana apropiada sugiere las raíces\(x=2\) y\(x=5\).
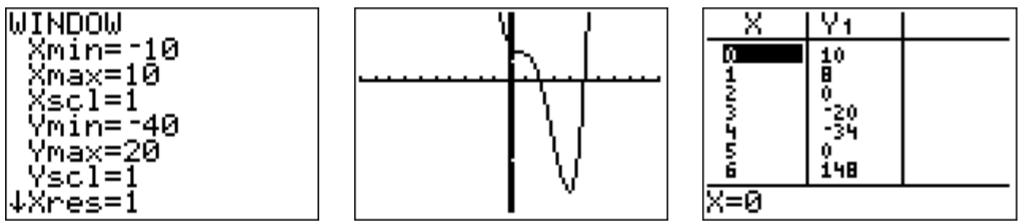
Dividir\(f(x)\) por\((x-2)(x-5)=x^2-7x+10\) da:
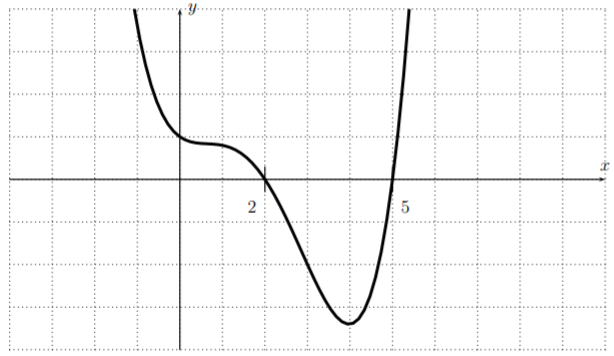
Dado que las raíces de\(x^2+1\) son todas complejas, vemos que las únicas raíces de\(f\) son\(x=2\) y\(x=5\). La gráfica incluyendo sus raíces se muestra a continuación.
Encuentra un polinomio\(f\) con las siguientes propiedades.
- \(f\)tiene grado\(3\), las raíces de\(f\) son precisamente\(4\),\(5\),\(6\), y el coeficiente principal de\(f\) es\(7\)
- \(f\)tiene grado\(3\) con coeficientes reales,\(f\) tiene raíces\(3i\),\(-5\) (y posiblemente otras raíces también), y\(f(0)=90\)
- \(f\)tiene grado\(4\) con coeficientes complejos,\(f\) tiene raíces\(i+1\)\(2i\),\(3\)
- \(f\)tiene grado\(5\) con coeficientes reales, el coeficiente principal es 1, y las raíces están determinadas por su gráfica:
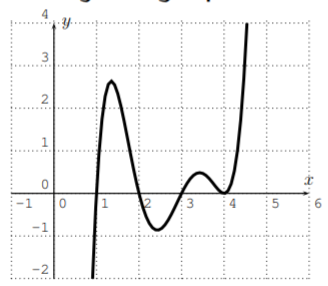
Solución
- En general un polinomio\(f\) de grado\(3\) es de la forma\(f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot (x-c_3)\). Identificando las raíces y el coeficiente principal, obtenemos el polinomio\[f(x)=7 \cdot (x-4)\cdot (x-5)\cdot (x-6) \nonumber \]
- Un polinomio\(f\) de grado\(3\) es de la forma\(f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot (x-c_3)\). Raíces de\(f\) son\(3i\) y\(-5\), y dado que los coeficientes de\(f\) son reales se deduce de la Observación Polinómica General (4), que el conjugado complejo\(-3i\) es también una raíz de \(f\). Por lo tanto,\(f(x)=m\cdot (x+5)\cdot (x-3i)\cdot (x+3i)\). Para identificar\(m\), utilizamos la última condición\(f(0)=90\). \[90 = m\cdot (0+5)\cdot (0-3i)\cdot (0+3i)=m\cdot 5\cdot (-9)i^2=m\cdot 5\cdot 9=45 m \nonumber \]Dividiendo por\(45\), obtenemos\(m=2\), de manera que\[f(x)=2\cdot (x+5)\cdot (x-3i)\cdot (x+3i)=2\cdot (x+5)\cdot (x^2+9) \nonumber \] aquello que claramente tenga coeficientes reales.
- Ya que\(f\) es de grado\(4\) se puede escribir como\(f(x)=m\cdot (x-c_1)\cdot (x-c_2)\cdot (x-c_3)\cdot (x-c_4)\). Tres de las raíces se identifican como\(i+1\),\(2i\), y\(3\):\[f(x)=m\cdot (x-(1+i))\cdot (x-2i)\cdot (x-3)\cdot (x-c_4) \nonumber \] Sin embargo, no tenemos más información sobre la cuarta raíz\(c_4\) o el coeficiente principal\(m\). (Obsérvese que la Observación Polinómica General (4) no se puede utilizar aquí, ya que no estamos asumiendo que el polinomio tenga coeficientes reales. En efecto, no puede tener coeficientes reales ya que eso significaría que tendríamos también los complejos conjugados de\(1+i\) y\(2i\) además de los tres que se nos dan, dándonos un total de 5 raíces que no pueden ser acomodadas por un polinomio de grado 4.) Por lo tanto, podemos elegir cualquier número para estas variables restantes. Por ejemplo, se da una posible solución del problema eligiendo\(m=3\) y\(c_4=2\), para lo cual obtenemos:\[f(x)=3\cdot (x-(1+i))\cdot (x-2i)\cdot (x-3)\cdot (x-2) \nonumber \]
- \(f\)es de grado\(5\), y sabemos que el coeficiente principal es\(1\). La gráfica es cero en\(x=1, 2, 3\), y\(4\), para que las raíces sean\(1\),\(2\),\(3\), y\(4\). Además, dado que la gráfica apenas toca la raíz\(x=4\), ésta debe ser una raíz múltiple, es decir, debe ocurrir más de una vez (ver Sección 9.3 para una discusión de múltiples raíces y sus consecuencias gráficas). Obtenemos la siguiente solución:\[f(x)=(x-1)(x-2)(x-3)(x-4)^2 \nonumber \] Obsérvese que la raíz\(x=4\) es una raíz de multiplicidad\(2\).
Tenga en cuenta que para ver que un polinomio tiene coeficientes reales, puede ser necesario multiplicar factores como\((x-(2+3i))(x-(2-3i))\). Sugerimos una forma de hacer esto para lo cual utilizamos el hecho de que\(a^2-b^2=(a+b)(a-b)\). Tenemos\[(x-(2+3i))(x-(2-3i))=((x-2)-3i)((x-2)+3i)=(x-2)^2+9 \nonumber \] lo que claramente tiene coeficientes reales.