16.1: Vida media

Última actualización
Guardar como PDF

Page ID: 117780

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

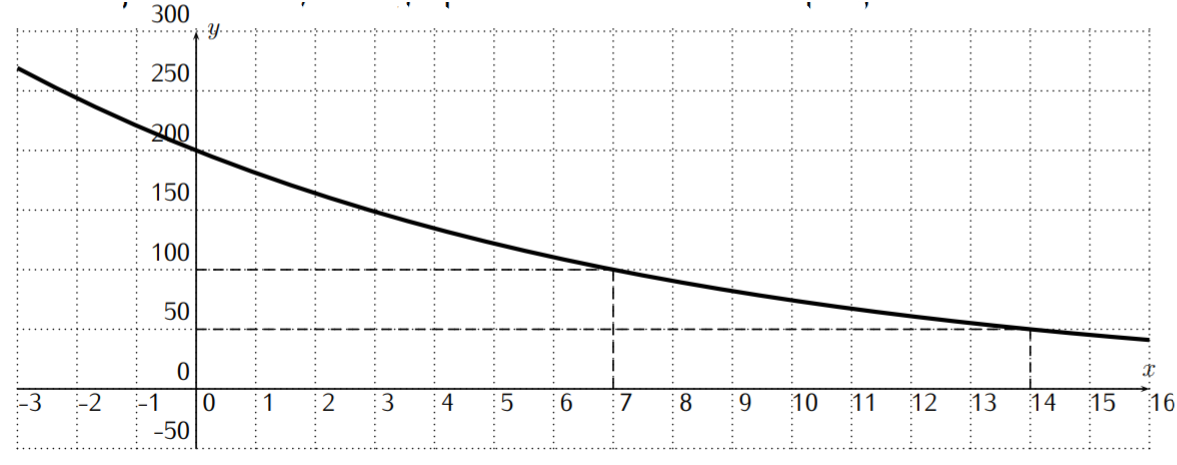
Recordemos de la definición Tasa de crecimiento en la página que una función con tasa de crecimiento$r$ es una función exponencial$f(x)=c\cdot b^x$ con base$b=1+r$. También hay otra forma importante de determinar la base de una función exponencial, la cual viene dada por la noción de vida media. Empezamos con un ejemplo motivador. Considera la función$f(x)=200\cdot \left(\dfrac 1 2\right)^{\frac x 7}$. Calculamos los valores de las funciones$f(x)$$x=0$, for$7$,$14$,$21$, y$28$.

\[\begin{aligned} f(0)&=200\cdot \left(\dfrac 1 2\right)^{\frac 0 7}= 200 \cdot 1=200\\ f(7)&=200\cdot \left(\dfrac 1 2\right)^{\frac 7 7}= 200 \cdot \dfrac 1 2=100\\ f(14)&=200\cdot \left(\dfrac 1 2\right)^{\frac {14} 7}= 200 \cdot \dfrac 1 4=50\\ f(21)&=200\cdot \left(\dfrac 1 2\right)^{\frac {21} 7}= 200 \cdot \dfrac 1 8=25\\ f(28)&=200\cdot \left(\dfrac 1 2\right)^{\frac {28} 7}= 200 \cdot \dfrac 1 {16}=12.5\\\end{aligned} \nonumber \]

A partir de este cálculo, podemos ver cómo$f$ se comportan los valores de la función: a partir de$f(0)=200$, la función toma la mitad de su valor cada vez que$x$ se incrementa en$7$. Por ello, decimos que$f$ tiene una vida media de$7$. (A continuación se dará la definición general.) A continuación se muestra el gráfico de la función.

$clipboard_e210fd5df8a7eff88f890f152d0383a27.png$

Recopilamos las ideas que se muestran en el ejemplo anterior en la definición y observación a continuación.

Definición: Half-Vida

Dejar$f$ ser una función exponencial$f(x)=c\cdot b^x$ con un dominio de todos los números reales,$D=\mathbb{R}$. Entonces decimos que$f$ tiene una vida media de$h$, si la base viene dada por

\[\label{half-life-base} \boxed{\,\, b=\left(\dfrac 1 2\right)^{\frac 1 h} \,\,}\]

Tenga en cuenta que también podemos escribir$h$ en términos de$b$. La conversión$\ref{half-life-base}$ en una ecuación logarítmica da$\dfrac 1 h = \log_{\frac 1 2} (b)=\dfrac{\log b}{\log \frac 1 2}$, así que eso$h=\dfrac{\log \frac 1 2}{\log{b}}=\log_b\left(\dfrac 1 2\right)$.

Dejar$f$ ser la función exponencial dada para algunas constantes reales$c>0$ y vida media$h>0$, es decir

\[f(x)=c\cdot \left(\left(\dfrac 1 2\right)^{\frac 1 h}\right)^x=c\cdot \left(\dfrac 1 2 \right)^{\frac x h} \nonumber \]

Entonces podemos calcular de la$f(x+h)$ siguiente manera:

\[\begin{aligned} f(x+h) &= c\cdot \left(\dfrac 1 2\right)^{\frac {x+h} h}=c\cdot \left(\dfrac 1 2\right)^{\frac x h+\frac h h}=c\cdot \left(\dfrac 1 2\right)^{\frac {x} h +1} \\ &=& c\cdot \left(\dfrac 1 2\right)^{\frac {x} h}\cdot \left(\dfrac 1 2\right)^1=\dfrac 1 2 \cdot f(x) \end{aligned} \nonumber \]

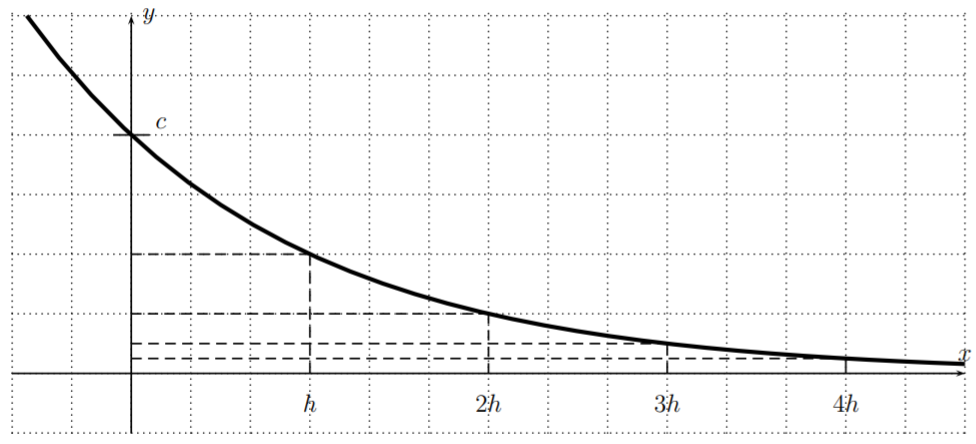
Para resumir,$f$ tiene la siguiente propiedad:

\[\boxed{f(x+h)=\dfrac 1 2 f(x)} \quad\quad \text{for all }x \in \mathbb{R}.\]

La ecuación anterior muestra que, cada vez que agregamos una cantidad de$h$ a una entrada$x$, el efecto sobre$f$ es que el valor de la función disminuye a la mitad de su valor anterior. Esto también se muestra en la gráfica a continuación.

$clipboard_eb51175577fb95bda00432c51f30af123.png$

A veces usaremos una letra diferente para la variable de entrada. En particular, la función$f(x)=c\cdot \left(\dfrac 1 2\right)^{\frac x h}$ es la misma que la función$f(t)=c\cdot \left(\dfrac 1 2\right)^{\frac t h}$.

Ejemplo$\PageIndex{1}$

Muchos isótopos radiactivos se desintegran con vidas medias conocidas.

El cromo-51 tiene una vida media de$27.7$ días ¹. ¿Cuánto de$3$ gramos de cromo-51 quedarán después de$90$ días?
Un isótopo se descompone en cuestión de$20$ horas de$5$ gramos a$2.17$ gramos. Encuentra la vida media del isótopo.

Solución

Utilizamos la fórmula anterior$y=c\cdot \left(\dfrac 1 2\right)^{\frac t h}$, donde$c=3$ gramos es la cantidad inicial de cromo-51,$h=27.7$ días es la vida media de cromo-51, y$t=90$ días es el tiempo en que el isótopo se descomponen. Sustituyendo estos números en la fórmula para$y$, obtenemos:

\[y=3\cdot \left(\dfrac 1 2\right)^{\frac {90}{27.7}}\approx 0.316 \nonumber \]

Por lo tanto, después de$90$ días, quedan$0.316$ gramos del cromo-51.

Tenemos una cantidad inicial de$c=5$ gramos y una cantidad restante de$y=2.17$ gramos después de$t=20$ horas. La vida media se puede obtener de la siguiente manera.

\ [\ begin {alineado}
2.17&=5\ cdot\ izquierda (\ dfrac 1 2\ derecha) ^ {\ frac {20} {h}}\
\ implica 0.434&=\ izquierda (\ dfrac 1 2\ derecha) ^ {\ frac {20} {h}}\ quad\ text {($\ div 5$)}\
\ implica\ ln (0.434) &=\ ln\ izquierda (0.5^ {\ frac {20} h}\ derecha)\ quad\ text {(aplicar $\ ln$)}\\
\ implica\ ln (0.434) &=\ dfrac {20} h\ cdot\ ln\ izquierda (0.5\ derecha)\
\ implica h&=\ dfrac {{20}\ cdot\ ln (0.5)} {\ ln (0.434)}\ quad\ izquierda (\ times\ dfrac {h} {\ ln (0.434)}\ derecha)\
\ implica t &\ aproximadamente 16.6
\ final {alineado}\ nonumber\]

Por lo tanto, la vida media del isótopo es de aproximadamente$16.6$ horas.

Un isótopo importante es el radioisótopo carbono-14. Decae con una vida media de$5730$ años con una precisión de$\pm 40$ años. Por definición tomaremos$5730$ años como la vida media del carbono-14.

\[\boxed{\text{The half-life of carbon-14 is $5730$ years.}}\]

Se puede utilizar el conocimiento de la vida media del carbono-14 en la datación de materiales orgánicos a través del llamado método de datación por carbono. El carbono-14 es producido por una planta durante el proceso de fotosíntesis a un nivel fijo hasta que la planta muere. Por lo tanto, al medir la cantidad restante de carbono-14 en una planta muerta se puede determinar la fecha en que murió la planta. Además, dado que los humanos y los animales consumen plantas, se puede aplicar el mismo argumento para determinar sus fechas (aproximadas) de muerte.

Ejemplo$\PageIndex{2}$

Un tronco de árbol muerto tiene$86\%$ de su carbono-14 original. (Aproximadamente) ¿cuántos años atrás murió el árbol?
Un animal muerto en un sitio arqueológico ha perdido$41.3\%$ de su carbono-14. ¿Cuándo murió el animal?

Solución

Usando la función$y=c\cdot \left(\dfrac 1 2\right)^{\frac t h}$, donde$c$ está la cantidad de carbono-14 que fue producida por el árbol hasta que murió,$y$ es la cantidad restante hasta la fecha,$t$ es el tiempo que ha pasado desde que el árbol murió, y$h$ es la vida media del carbono-14. Ya que$86\%$ del carbono-14 queda, tenemos$y=86\%\cdot c$. Sustituyendo la vida media$h=5730$ del carbono-14, podemos resolver para$t$.

\ [\ begin {alineado}
0.86\ cdot c&=c\ cdot\ izquierda (\ dfrac 1 2\ derecha) ^ {\ frac t {5730}}\
\\ implica 0.86&=\ izquierda (\ dfrac 1 2\ derecha) ^ {\ frac t {5730}}\ quad\ text {($\ div c$)}\
\ implica\ ln (86) &=\ ln\ izquierda (0.5^ {\ frac t {5730}}\ derecha)\ quad\ text {(aplicar $\ ln$)}\\
\ ln (0.86) &=\ dfrac t {5730}\ cdot\ ln\ izquierda (0.5\ derecha)\
\ dfrac {5730} {\ ln (0.5)}\ cdot\ ln (0.86) &=t\ quad\ izquierda (\ times\ dfrac {5730} {\ ln (0.5)}\ derecha)\
\ implica t &\ aprox 1247
\ fin {alineado}\ nonumber\]

Por lo tanto, el árbol murió aproximadamente hace$1247$ años.

Ya que$41.3\%$ del carbono-14 se ha ido,$100\%-41.3\%=58.7\%$ queda. Usando$y=c\cdot \left(\dfrac 1 2\right)^{\frac{t}{h}}$ con$y=58.7\%\cdot c$ y$h=5730$, obtenemos

\ [\ begin {alineado}
0.587\ cdot c&=c\ cdot\ izquierda (\ dfrac 1 2\ derecha) ^ {\ frac t {5730}}\\
\ implica 0.587&=\ izquierda (\ dfrac 1 2\ derecha) ^ {\ frac t {5730}}\ quad\ text {($\ div c$)}\
\ implica\ ln (0.587) &=\ ln\ izquierda (0.5^ {\ dfrac t {5730}}\ derecha)\ quad\ text {(aplicar $\ ln$)}\\
\ implica\ ln (0.587) &=\ dfrac t {5730}\ cdot\ ln\ izquierda (0.5\ derecha)\
\ dfrac {5730} {\ ln (0.5)}\ cdot\ ln (0.587) &=t\ quad\ izquierda (\ times\ dfrac {5730} {\ ln (0.5)}\ derecha)\\
t &\ aprox 4404
\ fin {alineado}\ nonumber\]

El animal murió hace$4404$ años.

Referencias

Las vidas medias se toman de: https://en.Wikipedia.org/wiki/List_o...fe#100_seconds

Definición: Half-Vida

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Referencias