16.2: Interés Compuesto

Existe otra aplicación interesante e importante de la función exponencial dada al calcular el interés sobre una inversión. Comenzamos con el siguiente ejemplo motivador.

Ejemplo\(\PageIndex{1}\)

• Invertimos una cantidad inicial de\(P=\$500\) por\(1\) año a una tasa de\(r=6\%\). El monto inicial también\(P\) se llama el principal.

  Después\(1\) del año, recibimos el principal\(P\) junto con los intereses\(r\cdot P\) generados por el principal. Por lo tanto, el monto final\(A\) después\(1\) del año es

  \[A=\$ 500+ 6\%\cdot \$ 500=\$500 \cdot(1+0.06)= \$ 530 \nonumber \]

• Cambiamos la configuración del ejemplo anterior tomando una composición trimestral. Esto significa, que en lugar de recibir intereses sobre el principal una vez al final del año, recibimos los\(4\) tiempos de interés dentro del año (después de cada trimestre). No obstante, ahora solo recibimos\(\dfrac{1}{4}\) de la tasa de interés de\(6\%\). Desglosamos la cantidad recibida después de cada trimestre.

  \ [\ begin {aligned}
  \ text {después del primer trimestre:}\ quad 500\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) &= {\ color {Rojo} 500\ cdot 1.015}\\ texto {después del segundo trimestre:}\ quad ({\ color {Rojo} 500\ cdot 1.015})\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) &= {\ color {Azul} 500\ cdot 1.015^2}\\
  \ texto { después del tercer trimestre:}\ quad ({\ color {Azul} 500\ cdot 1.015^2})\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) &= {\ color {Verde} 500\ cdot 1.015^3}\
  \ texto {después del cuarto trimestre:}\ quad A&= ({\ color {Verde} 500\ cdot 1.015^3})\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) =500\ cdot 1.015^4\
  \ implica A&\ approx 530.68
  \ end {alineado}\ nonumber\]

  Tenga en cuenta que en el segundo trimestre, recibimos intereses sobre la cantidad que teníamos después del primer trimestre, y así sucesivamente. Entonces, de hecho, seguimos recibiendo intereses sobre los intereses de los intereses, etc. Por esta razón, el monto final recibido después del\(1\) año\(A=\$ 530.68\) es ligeramente mayor cuando se compone trimestralmente que cuando se compone anualmente (donde\(A=\$ 530.00\)).

• Hacemos una variación aún mayor de lo anterior. En lugar de invertir dinero por\(1\) año, invertimos el principal durante\(10\) años en una composición trimestral. Luego recibimos intereses cada trimestre por un total de\(4\cdot 10=40\) trimestres.

  \ [\ begin {aligned}
  \ text {después del primer trimestre:}\ quad 500\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) &=500\ cdot 1.015\
  \ text {después del segundo trimestre:}\ quad (500\ cdot 1.015)\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) &=500\ cdot 1.015^2\\\ quad &\ vdots\\
  \ text { después del cuadragésimo trimestre:}\ quad A&= (500\ cdot 1.015^ {39})\ cdot\ Grande (1+\ dfrac {0.06} {4}\ Grande) =500\ cdot 1.015^ {40}\
  \ implica A &\ aprox 907.01
  \ end {alineado}\ nonumber\]

Declaramos nuestras observaciones del ejemplo anterior en la siguiente observación general.

Observación:\(n\)th-Compounding

Un principal (=monto inicial)\(P\) se invierte por\(t\) años a una tasa\(r\) y\(n\) tiempos compuestos por año. El monto final\(A\) viene dado por

\ [\ en caja {A=P\ cdot\ izquierda (1+\ frac {r} {n}\ derecha) ^ {n\ cdot t}}\ text {donde}\ left\ {\ begin {array} {l}
P=\ text {principal} (=\ text {inicial})\ text {cantidad}\\
A=\ texto {importe final}\\
r=\ text {tasa de interés anual}\\
n=\ texto {número de compuestos por año}\\
t=\ texto {número de años}
\ fin {array}\ derecho.\]

Podemos considerar realizar la composición en incrementos cada vez más pequeños. En lugar de la composición trimestral, podemos tomar compuestos mensuales, o diarios, por hora, en segundo lugar compuestos o compuestos en intervalos de tiempo aún más pequeños. Obsérvese, que en este caso el número de compuestos\(n\) en la fórmula anterior tiende al infinito. En el límite cuando los intervalos de tiempo van a cero, obtenemos lo que se llama compounding continuo.

Observación: Compuesto continuo

Un monto principal\(P\) se invierte por\(t\) años a una tasa\(r\) y con composición continua. El monto final\(A\) viene dado por

\ [\ boxed {A=P\ cdot e^ {r\ cdot t}}\ quad\ text {donde}\ left\ {\ begin {array} {l}
P=\ text {monto principal}\\
A=\ texto {importe final}\\
r=\ texto {tasa de interés anual}\\
t=\ texto {número de años}
\ end {array}\ derecha.\]

Nota

La razón por la que la función exponencial aparece en la fórmula anterior es que la exponencial es el límite de la fórmula anterior en observación\(n\) th-compounding, cuando se\(n\) acerca al infinito; compárelo con la ecuación 13.1.1.

\[e^r=\lim_{n\to \infty} \left(1+\dfrac r n\right)^n \nonumber \]

Se brindará una discusión más detallada de los límites (incluida su definición) en un curso de cálculo.

Ejemplo\(\PageIndex{1}\)

Determinar el monto final recibido de una inversión en las condiciones dadas.

1. \(\$700\), compuesto mensual, a\(4\%\), por\(3\) años
2. \(\$2500\), compuesto semestralmente, a\(5.5\%\), por\(6\) años
3. \(\$1200\), compuesto continuamente, a\(3\%\), durante\(2\) años

Solución

Podemos usar inmediatamente la fórmula sustituyendo los valores dados.

1. Para la parte (a), tenemos\(P=700\),\(n=12\),\(r=4\%=0.04\), y\(t=3\). Por lo tanto, calculamos

\[A=700\cdot\left(1+\dfrac{0.04}{12}\right)^{12\cdot 3}=700\cdot\left(1+\dfrac{0.04}{12}\right)^{36}\approx 789.09 \nonumber \]

2. Tenemos\(P=2500\),\(n=2\),\(r=5.5\%=0.055\), y\(t=6\).

\[A=2500\cdot\left(1+\dfrac{0.055}{2}\right)^{2\cdot 6}\approx 3461.96 \nonumber \]

3. Tenemos\(P=1200\),\(r=3\%=0.03\),\(t=2\), y usamos la fórmula para la composición continua.

\[A=1200\cdot e^{0.03\cdot 2}=1200 \cdot e^{0.06} \approx 1274.20 \nonumber \]

(Tenga en cuenta que el número de Euler se ingresa en el TI-84 a través de las claves y\(\boxed { \text {ln}}\).)

En lugar de pedir encontrar el monto final, también podemos preguntar por cualquiera de las otras variables en las fórmulas anteriores para inversiones.

Ejemplo\(\PageIndex{1}\)

1. Encuentra la cantidad\(P\) que se necesita invertir en\(4.275 \%\) compuesto anualmente\(5\) durante años para dar una cantidad final de\(\$ 3000\). (Esta cantidad también\(P\) se llama el valor presente de la cantidad futura de\(\$3000\) en\(5\) años.)
2. ¿A qué tasa tenemos que invertir\(\$800\) durante\(6\) años compuestos trimestralmente para obtener un monto final de\(\$1200\)?
3. ¿Por cuánto tiempo tenemos que invertir\(\$1000\) a una tasa de\(2.5 \%\) compuesto continuamente para obtener una cantidad final de\(\$1100\)?
4. ¿Por cuánto tiempo tenemos que invertir a una tasa de\(3.2\%\) compuestos mensuales hasta que la inversión duplique su valor?

Solución

1. Tenemos los siguientes datos:\(r=4.275\%=0.04275\),\(n=1\)\(t=5\), y\(A=3000\). Queremos encontrar el valor actual\(P\). Sustituyendo los números dados en la fórmula apropiada, podemos resolver esto para\(P\).

\ [\ begin {alineado}
3000&=P\ cdot\ izquierda (1+\ dfrac {0.04275} {1}\ derecha) ^ {1\ cdot 5}\
\\ implica 3000&=P\ cdot\ izquierda (1.04275\ derecha) ^ {5}\
\ implica P&=\ dfrac {3000} {1.04275^5}\ approx 2433.44\\ text {(dividir por $1.04275^5$)}
\ end {alineado}\ nonumber \]

Por lo tanto, si invertimos\(\$2433.44\) hoy bajo las condiciones dadas, entonces esto valdrá\(\$3000\) en\(5\) años.

2. Sustituir los números dados (\(P=800\),\(t=6\),\(n=4\),\(A=1200\)) en la fórmula da:

\ [\ begin {aligned}
1200&=800\ cdot\ izquierda (1+\ dfrac {r} {4}\ derecha) ^ {4\ cdot 6}\\\ implica
\ dfrac {1200} {800} &=\ izquierda (1+\ dfrac r 4\ derecha) ^ {24}\ quad\ text {(dividir por $800$)}\\ implica
\ izquierda (1+\ izquierda (1+\ dfrac r 4\ derecha) ^ {24} &=\ dfrac {3} {2}
\ final {alineado}\ nonumber\]

A continuación, tenemos que llevar al exponente\(24\) al lado derecho. Esto se hace tomando un poder de\(\dfrac{1}{24}\), o en otras palabras, tomando la raíz\(24\) th,\(\sqrt[24]{\dfrac{3}{2}}=\Big(\dfrac{3}{2}\Big)^{\frac{1}{24}}\).

\ [\ begin {alineado}
\ izquierda (\ izquierda (1+\ dfrac {r} {4}\ derecha) ^ {24}\ derecha) ^ {\ frac {1} {24}} &=\ izquierda (\ dfrac {3} {2}\ derecha) ^ {\ frac {1} {24}}\
\ implica\ izquierda (1+\ dfrac {r} {4}\ derecha) ^ {24\ cdot\ frac {1} {24}} &=\ izquierda (\ dfrac {3} {2}\ derecha) ^ {\ frac {1} {24}}\\ implica 1+\ dfrac {r} {4} &=\ izquierda (\ frac {3} {2}\ derecha) ^ {\ frac {1} {24}}\
\ implica\ dfrac {r} {4} &=\ izquierda (\ dfrac {3} {2}\ derecha) ^ {\ frac {1} {24}} -1\
\ implica r&=4\ cdot\ izquierda (\ izquierda (\ dfrac {3} {2}\ derecha) ^ {\ frac {1} {24}} -1\ derecha)
\ final {alineado}\ nonumber\]

Conectamos esto a la calculadora. Tenga en cuenta que la raíz\(n\) th se da presionando\(\boxed {\text{math}}\) y.

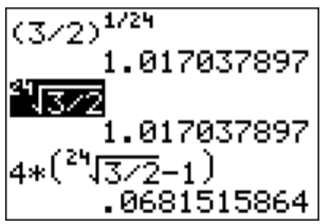
Más precisamente, la raíz\(24\) th de\(3/2\) (resaltada arriba) se puede ingresar presionando las siguientes teclas:

\(\boxed {2}\)\(\boxed {4}\)\(\boxed {\text{math}}\)\(\boxed {5}\)\(\boxed {3}\)\(\boxed {\div}\)\(\boxed {2}\)\(\boxed {\text{enter}}\)

Por lo tanto nuestra respuesta es\(r\approx 0.06815 =6.815\%\).

3. Nuevamente sustituimos los valores dados\(P=1000\),\(r=2.5\%=0.025\),\(A=1100\), pero ahora usamos la fórmula para la composición continua.

\[1100=1000\cdot e^{0.025\cdot t} \implies \quad \dfrac{1100}{1000}= e^{0.025\cdot t}\implies \quad e^{0.025\cdot t}=1.1 \nonumber \]

Para resolver para la variable\(t\) en el exponente, necesitamos aplicar el logaritmo. Aquí, lo más conveniente es aplicar el logaritmo natural, porque\(\ln(x)\) es inverso a\(e^x\) (que aparece en la ecuación) y este logaritmo se implementa directamente en la calculadora a través de la\(\boxed {\text{ln}}\) clave. Al aplicar\(\ln\) a ambos lados, ya que\(\ln(x)\) es inverso a\(e^x\), vemos eso\(.025 t=\ln(1.1)\).

Alternativamente,

\[\ln(e^{0.025\cdot t})=\ln(1.1)\quad \implies \quad 0.025\cdot t\cdot \ln(e)=\ln(1.1) \nonumber \]

Aquí hemos usado eso\(\log_b(x^n)=n\cdot \log_b(x)\) para cualquier número\(n\) como hemos visto en proposición propiedades logarítmicas. Observando que\(\ln(e)=1\), que es el caso especial de la segunda ecuación en [elementary-log] en la página para la base\(b=e\), lo anterior se convierte

\[0.025\cdot t=\ln(1.1) \quad \implies \quad t=\dfrac{\ln(1.1)}{0.025}\approx 3.81 \nonumber \]

Por lo tanto, tenemos que esperar\(4\) años hasta que la inversión valga (más que)\(\$1100\).

4. Se nos da eso\(r=3.2\%=0.032\) y\(n=12\), pero no\(P\) se proporciona ninguna cantidad inicial. Buscamos encontrar el momento en que la inversión\(t\) se duplique. Esto significa que la cantidad final\(A\) es el doble de la cantidad inicial\(P\), o como fórmula:\(A=2\cdot P\). Sustituir esto en la fórmula de inversión y resolver da la respuesta deseada.

\ [\ begin {aligned}
2P&=P\ cdot\ left (1+\ dfrac {0.032} {12}\ derecha) ^ {12\ cdot t}\
\\ implica 2&=\ left (1+\ dfrac {0.032} {12}\ derecha) ^ {12\ cdot t}\ qquad\ text {(dividir por $P$)}\
\ implica\\ ln (2) &=\ ln\ izquierda (\ izquierda (1+\ dfrac {0.032} {12}\ derecha) ^ {12\ cdot t}\ derecha)\ qquad\ text {(aplicar $\ ln$)}\\
\ implica\ ln (2) &= 12\ cdot t\ cdot\ ln\ izquierda (1+\ dfrac {0.032} {12}\ derecha)\
\ implica t&=\ dfrac {\ ln (2)} {12\ cdot\ ln\ izquierda (1+\ dfrac {0.032} {12} derecha)}\ qquad\ texto {dividir por)} 12\ cdot\ ln\ izquierda (1+\ dfrac {0.032} {12}\ derecha)\\
&\ aprox 21. 69
\ final {alineado}\ nonumber\]

Entonces, después de aproximadamente\(21.69\) años, la inversión se habrá duplicado en valor.