24.2: Serie Geométrica Infinita
- Page ID
- 117699
En algunos casos, tiene sentido agregar no solo finitamente muchos términos de una secuencia geométrica, ¡sino todos infinitamente muchos términos de la secuencia! En el siguiente ejemplo se exhibe una serie geométrica infinita informal y muy intuitiva.
Considera la secuencia geométrica\[1, \dfrac 1 2, \dfrac 1 4, \dfrac 1 8, \dfrac 1 {16}, \dots \nonumber \]
Solución
Aquí, la relación común es\(r=\dfrac 1 2\), y el primer término es\(a_1=1\), de manera que la fórmula para\(a_n\) es\(a_n=\left(\dfrac 1 2\right)^{n-1}\). Nos interesa sumar infinitamente muchos términos de esta secuencia:
\[1+ \dfrac 1 2+ \dfrac 1 4+ \dfrac 1 8+\dfrac 1 {16}+ \dots \nonumber \]
Agregamos estos términos uno por uno, e imaginamos estas sumas en la recta numérica:
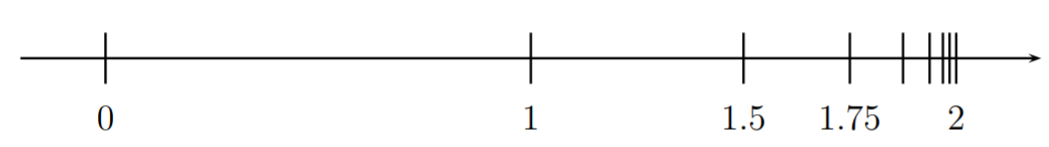
\[\begin{aligned} 1&= 1\\ 1+\dfrac 1 2&= 1.5\\ 1+\dfrac 1 2+\dfrac 1 4&= 1.75\\ 1+\dfrac 1 2+\dfrac 1 4+\dfrac 1 8 &= 1.875\\ 1+\dfrac 1 2+\dfrac 1 4+\dfrac 1 8+\dfrac 1 {16} &= 1.9375\end{aligned} \nonumber \]
Vemos que sumar cada término lleva la suma cada vez más cerca del número\(2\). Más precisamente, agregar un término\(a_n\) a la suma parcial\(a_1+\dots+a_{n-1}\) corta la distancia entre\(2\) y a\(a_1+\dots+a_{n-1}\) la mitad. Por esta razón podemos, de hecho, acercarnos arbitrariamente\(2\), de manera que es razonable esperar que
\[1+ \dfrac 1 2+ \dfrac 1 4+ \dfrac 1 8+\dfrac 1 {16}+ \dots =2 \nonumber \]
En la siguiente definición y observación, esta ecuación se justificará y se hará más precisa. Comenzamos aportando la definición de una serie infinita.
Una serie infinita viene dada por el
\[\sum_{i=1}^\infty a_i = a_1+a_2+a_3+\dots\]
Para ser más precisos, la suma infinita se define como el límite\(\sum\limits_{i=1}^\infty a_i := \lim\limits_{k\to \infty} \bigg(\sum\limits_{i=1}^k a_i\bigg)\). Por lo tanto, se define una suma infinita, precisamente cuando existe este límite.
Dejar\(\{a_n\}\) ser una secuencia geométrica con\(a_n=a_1\cdot r^{n-1}\). Entonces la serie geométrica infinita se define siempre que sea\(-1<r<1\). En este caso, tenemos:
\[\label{EQU:inf-geo-series} \boxed{ \sum_{i=1}^\infty a_i = a_1\cdot \dfrac{1}{1-r} }\]
- Prueba
-
De manera informal, esto se desprende de la fórmula\(\sum_{i=1}^k a_i = a_1\cdot \dfrac{1-r^{k}}{1-r}\) y el hecho de que se\(r^k\) acerca a cero cuando\(k\) aumenta sin límite.
De manera más formal, la prueba utiliza la noción de límites, y va de la siguiente manera:
\[\sum_{i=1}^\infty a_i = \lim_{k\to \infty}\bigg( \sum_{i=1}^k a_i \bigg) = \lim_{k\to \infty}\bigg( a_1\cdot \frac{1-r^{k}}{1-r}\bigg) = a_1\cdot \frac{1-\lim\limits_{k\to\infty } (r^{k})}{1-r} = a_1\cdot \dfrac{1}{1-r} \nonumber \]
Encuentra el valor de la serie geométrica infinita.
- \(\sum_{j=1}^\infty a_j\), para\(a_j=5\cdot \left(\dfrac 1 3\right)^{j-1}\)
- \(\sum_{n=1}^\infty 3\cdot \left(0.71\right)^n\)
- \(500-100+20-4+\dots\)
- \(3+6+12+24+48+\dots\)
Solución
- Utilizamos fórmula\(\ref{EQU:inf-geo-series}\) para la serie geométrica\(a_n=5\cdot \left(\dfrac 1 3\right)^{n-1}\), es decir\(a_1=5\cdot \left(\dfrac 1 3\right)^{1-1}=5\cdot \left(\dfrac 1 3\right)^{0}=5\cdot 1 =5\) y\(r=\dfrac 1 3\). Por lo tanto,
\[\sum_{j=1}^\infty a_j=a_1\cdot \dfrac {1}{1-r}=5\cdot \dfrac {1}{1-\frac 1 3}=5\cdot \dfrac 1 {\frac{3-1}{3}}=5\cdot \dfrac 1 {\frac 2 3}=5\cdot \dfrac 3 2 =\dfrac {15} 2 \nonumber \]
- En este caso,\(a_n=3\cdot (0.71)^n\), para que\(a_1=3\cdot 0.71^1=3\cdot 0.71=2.13\) y\(r=0.71\). Usando nuevamente la fórmula\(\ref{EQU:inf-geo-series}\), podemos encontrar la serie geométrica infinita como
\[\sum_{n=1}^\infty 3\cdot \left(0.71\right)^n=a_1\cdot \dfrac{1}{1-r}=2.13\cdot \dfrac 1 {1-0.71}=2.13\cdot \dfrac 1 {0.29}=\dfrac {2.13}{0.29}=\dfrac{213}{29} \nonumber \]
En el último paso simplificamos la fracción multiplicando tanto el numerador como el denominador por\(100\), lo que tuvo el efecto de eliminar los decimales.
- Nuestra primera tarea es identificar la secuencia dada como una secuencia geométrica infinita:
\[\{a_n\} \text{ is given by } 500, -100, 20, -4, \dots \nonumber \]
Observe que el primer término es\(500\), y cada término consecutivo se da dividiendo por\(-5\), o en otras palabras, multiplicando por la proporción común\(r=-\dfrac 1 5\). Por lo tanto, se trata de una serie geométrica infinita, que puede evaluarse como
\[\begin{aligned} 500-100+20-4+\dots &= \sum_{n=1}^\infty a_n\\&=a_1\cdot \dfrac 1 {1-r}\\&=500\cdot \dfrac 1 {1-\left(-\frac 1 5\right)} \\ &= 500 \cdot \dfrac{1}{1+\frac 1 5} \\&=\dfrac {500}{\frac {1+5}{5}}\\&=\dfrac{500}{\frac 6 5}\\&=500\cdot \dfrac 5 6 \\ &= \dfrac {2500}{6} \\&= \dfrac{1250}{3}\end{aligned} \nonumber \]
- Queremos evaluar la serie infinita\(3+6+12+24+48+\dots\). La secuencia\(3, 6, 12, 24, 48, \dots\) es una secuencia geométrica, con\(a_1=3\) una relación común\(r=2\). Ya que\(r\geq 1\), vemos que la fórmula\(\ref{EQU:inf-geo-series}\) no se puede aplicar, como\(\ref{EQU:inf-geo-series}\) sólo se aplica a\(-1<r<1\). Sin embargo, dado que agregamos términos cada vez más grandes, la serie se hace más grande que cualquier posible límite, de manera que toda la suma se vuelve infinita.
\[3+6+12+24+48+\dots=\infty \nonumber \]
La fracción\(0.55555\dots\) puede escribirse como:
\[0.55555\dots = 0.5+0.05+0.005+0.0005+0.00005+\dots \nonumber \]
Señalando que la secuencia
\[0.5,\underset{\times 0.1}{\hookrightarrow } 0.05, \underset{\times 0.1}{\hookrightarrow } 0.005, \underset{\times 0.1}{\hookrightarrow } 0.0005, \underset{\times 0.1}{\hookrightarrow } 0.00005, \dots \nonumber \]
es una secuencia geométrica con\(a_1=0.5\) y\(r=0.1\), podemos calcular la suma infinita como:
\[0.55555\dots = \sum_{i=1}^\infty 0.5 \cdot \left(0.1\right)^{i-1}= 0.5\cdot \dfrac{1}{1-0.1} = 0.5 \cdot\dfrac{1}{0.9}=\dfrac{0.5}{0.9}=\dfrac 5 9 \nonumber \]
Aquí multiplicamos el numerador y el denominador por\(10\) en el último paso para eliminar los decimales.


