Saltar al contenido principal
LibreTexts Español

25.1: El Teorema Binomial

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    117740

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Recordemos la conocida fórmula binomial:

    \[\boxed{(a+b)^2=a^2+2ab+b^2} \nonumber \]

    \[\text{(since, using ``FOIL,'' we have: } (a+b)^2=(a+b)\cdot (a+b) = a^2+ab+ab+b^2=a^2+2ab+b^2 \text{)} \nonumber \]

    En esta sección generalizamos esto para encontrar expresiones similares para\((a+b)^n\) para cualquier número natural\(n\). Este es el contenido del teorema binomial (generalizado) a continuación. Antes de que podamos exponer el teorema, necesitamos definir la noción de un factorial y combinaciones.

    Definición:\(n\) factorial

    Para un número natural\(n=1,2,3,\dots\),\(n!\) definimos como el número

    \[\boxed{n! = 1\cdot 2\cdot 3\cdot \dots \cdot n}\]

    El número\(n!\) se llama\(n\) factorial.

    Para que las fórmulas a continuación funcionen bien, también definimos\(0!\) ser\(0!=1\).

    Es fácil calcular algunos ejemplos de factoriales.

    Ejemplo\(\PageIndex{1}\)

    1. \(4!\)
    2. \(7!\)
    3. \(2!\)

    Solución

    1. \(4 !=1 \cdot 2 \cdot 3 \cdot 4=24\)
    2. \(7 !=1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7=5040\)
    3. \(2 !=1 \cdot 2=2\)

    Para calcular factoriales con la calculadora, tenemos que usar el menú MATH (presionar\(\boxed{\text{math}}\)), luego pasar al menú PRB (presionar\(\boxed{\triangleleft}\)), y usar el cuarto ítem (presionar\(\boxed{\text{4}}\)).

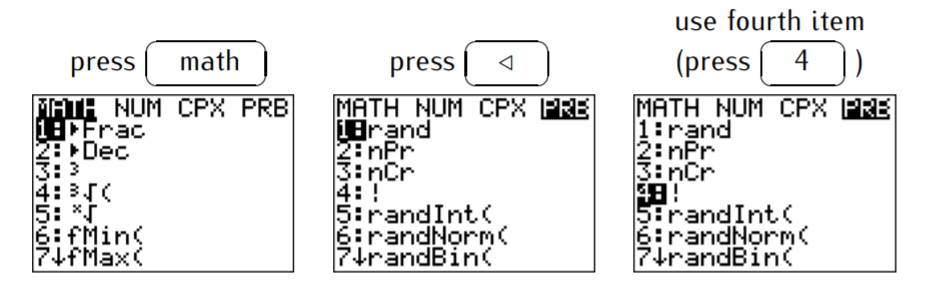
    clipboard_ea9eb3b7bc8b8dd7ccb17cc739dc4921c.png

    Por ejemplo, podemos calcular\(12!=479001600\) ingresando\(12\) y el símbolo factorial como se describió anteriormente.

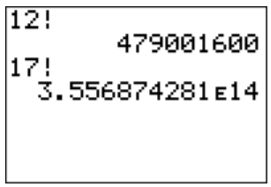
    clipboard_e1f1163298382709468376a9a87ee3548.png

    Tenga en cuenta que el factorial se vuelve muy grande incluso para enteros relativamente pequeños. Por ejemplo\(17!\approx 3.557\cdot 10^{14}\) como se muestra arriba. El siguiente concepto que introducimos es el del coeficiente binomial.

    Definición: Coeficiente binomial

    Dejar\(n=0,1,2,\dots\) y\(r=0,1,2,\dots,n\) ser números naturales o cero, así que eso\(0\leq r\leq n\). Luego definimos el coeficiente binomial como

    \[\binom{n}{r} = \dfrac{n!}{r!\cdot (n-r)!} \nonumber \]

    El coeficiente binomial también se escribe como\({ }_{n} C_{r}=\dbinom{n}{r}\), y los leemos como “\(n\)-elegir-” \(r\).

    Nota

    • El coeficiente binomial no\(\dbinom{n}{r}\) debe confundirse con la fracción\(\left(\dfrac{n}{r}\right)\).
    • Un subconjunto del conjunto\(\{1,2, \dots, n\}\) con\(r\) elementos se llama una\(r\) combinación -. El coeficiente binomial puede interpretarse como contar el número\(r\) de combinaciones distintas. Más precisamente, hay exactamente\(\dbinom{n}{r}\) distintas\(r\) -combinaciones del conjunto\(\{1,\dots, n\}\).

    Ejemplo\(\PageIndex{2}\)

    Calcular los coeficientes binomiales.

    1. \(\dbinom{6}{4}\)
    2. \(\dbinom{8}{5}\)
    3. \(\dbinom{25}{23}\)
    4. \(\dbinom{7}{1}\)
    5. \(\dbinom{11}{11}\)
    6. \(\dbinom{11}{0}\)

    Solución

    1. Muchos coeficientes binomiales pueden calcularse a mano, tales como:

    \[\dbinom{6}{4}=\dfrac{6!}{4!(6-4)!}= \dfrac{6!}{4!2!}=\dfrac{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6}{1\cdot 2\cdot 3\cdot 4\cdot 1\cdot 2}=\dfrac{5\cdot 6}{2}=15 \nonumber \]

    1. Nuevamente, podemos calcular esto a mano

    \[\dbinom{8}{5}=\dfrac{8!}{5!3!}=\dfrac{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7 \cdot 8}{1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 1\cdot 2 \cdot 3}=\dfrac{6\cdot 7\cdot 8}{1\cdot 2\cdot 3}=7\cdot 8 = 56 \nonumber \]

    Sin embargo, también podemos usar la calculadora para encontrar la respuesta. Usando los menús MATH y (presione\(\boxed{\text{math}}\)) PRB (presione\ boxed {\ triangleleft}\)) como arriba, usamos el tercer ítem (presione\(\boxed{\text{3}}\)). La respuesta se obtiene pulsando la siguiente secuencia de teclas:

    \ [\ begin {array} {|c|c|c|c|}
    \ hline 8 &\ text {math} &\ triangleleft & 3 & 5 &\ text {enter}\\
    \ hline
    \ end {array}\ nonumber\]

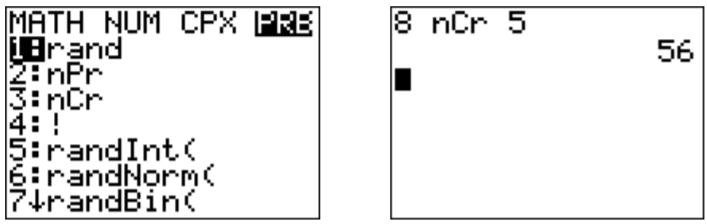
    clipboard_eda469eeb18704e6a502d049f004f3b4a.png

    También calculamos los coeficientes binomiales restantes (c) - (f), que también se pueden confirmar con la calculadora.

    1. \(\dbinom{25}{23}=\dfrac{25 !}{23 ! \cdot 2 !}=\dfrac{23 ! \cdot 24 \cdot 25}{23 ! \cdot 1 \cdot 2}=\dfrac{24 \cdot 25}{2}=300\)
    2. \(\dbinom{1}{7} = \dfrac{7 !}{1 ! \cdot 6 !}=\dfrac{6 ! \cdot 7}{1 \cdot 6 !}=\dfrac{7}{1}=7\)
    3. \(\dbinom{11}{11} = \dfrac{11 !}{11 ! \cdot 0 !}=\dfrac{1}{1 \cdot 1}=1\)
    4. \(\dbinom{11}{0} = \dfrac{11 !}{0 ! \cdot 11 !}=\dfrac{1}{1 \cdot 1}=1\)

    Tenga en cuenta que en las dos últimas ecuaciones necesitábamos usar el hecho de que\(0!=1\).

    Presentamos algunos datos útiles sobre el coeficiente binomial, que ya se pueden ver en el ejemplo anterior.

    Observación: Coeficiente binomial

    Para todos\(n=0,1,2,\dots\) y\(r=0, 1, 2, \dots, n\), tenemos:

    \[\boxed{\dbinom{n}{n-r}=\dbinom{n}{r}} \quad\quad \boxed{\dbinom{n}{0}=\dbinom{n}{n}=1} \quad\quad \boxed{\dbinom{n}{1}=\dbinom{n}{n-1}=n} \nonumber \]

    Prueba

    Contamos con:

    \[\begin{aligned} \dbinom{n}{n-r}&=\dfrac{n!}{(n-r)!\cdot (n-(n-r))!}=\dfrac{n!}{(n-r)!\cdot r!}=\dbinom{n}{r} \\ \dbinom{n}{0}&=\dbinom{n}{n}=\dfrac{n!}{0!\cdot n!}=\dfrac{1}{1}=1\\ \dbinom{n}{1}&=\dbinom{n}{n-1}=\dfrac{n!}{1!\cdot (n-1)!}=\dfrac{n}{1}=n\end{aligned} \nonumber \]

    Nota

    • Podemos obtener todos los coeficientes binomiales\(\dbinom{n}{r}\) para fijos\(n\) de la calculadora mediante el uso de los menús de función y tabla.

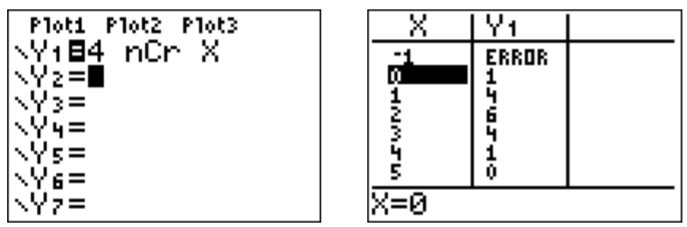
    clipboard_ef9016828d697a33dd4b966d274a3aa90.png

    • Los coeficientes binomiales se encuentran en lo que se conoce como triángulo de Pascal. Para ello, calcula los coeficientes binomiales más bajos y escríbelos en una disposición triangular:

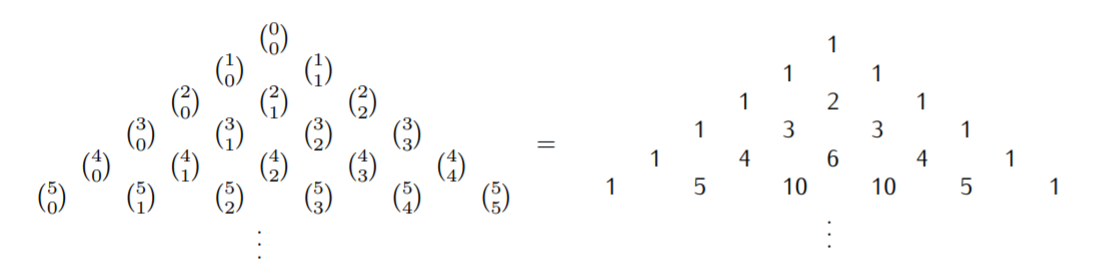
    clipboard_e68beb6035b928031da4c3018e9ca3a3f.png

    El triángulo de la derecha se conoce como triángulo de Pascal. Cada entrada en el triángulo se obtiene sumando las dos entradas justo encima de él.

    Los coeficientes binomiales aparecen en las expresiones para\((a+b)^n\) como veremos en el siguiente ejemplo. Ahora calculamos algunos ejemplos simples.

    Ejemplo\(\PageIndex{3}\)

    \[\begin{aligned} (a+b)^3 &= (a+b)\cdot (a+b)\cdot (a+b)\\ &= (a^2+2ab+b^2)\cdot (a+b)\\ &= a^3+2a^2b+ab^2+a^2b+2ab^2+b^3\\ &= a^3+3a^2b+3ab^2+b^3\end{aligned} \nonumber \]

    Obsérvese que los coeficientes\(1, 3, 3\), y\(1\) delante de\(a^3, a^2b, ab^2\)\(b^3\), y, respectivamente, son precisamente los coeficientes binomiales\(\dbinom 3 0, \dbinom 3 1, \dbinom 3 2\), y\(\dbinom 3 3\).

    También calculamos la cuarta potencia.

    \[\begin{aligned} (a+b)^4 &= (a+b)\cdot (a+b)\cdot (a+b)\cdot (a+b)\\ &= (a^3+3a^2b+3ab^2+b^3)\cdot (a+b)\\ &= a^4+3a^3b+3a^2b^2+ab^3+a^3b+3a^2b^2+3ab^3+b^4\\ &= a^4+4a^3b+6a^2b^2+4ab^3+b^4\end{aligned} \nonumber \]

    Nuevamente, los números\(1, 4, 6, 4\), y\(1\) son precisamente los coeficientes binomiales\(\dbinom 4 0, \dbinom 4 1, \dbinom 4 2, \dbinom 4 3\), y\(\dbinom 4 4\).

    Ahora estamos listos para exponer el teorema general del binomio.

    Teorema binomial

    La potencia\(n\) th se\((a+b)^n\) puede ampliar como:

    \[(a+b)^n= \dbinom{n}{0} a^n+\dbinom{n}{1} a^{n-1}b^1+\dbinom{n}{2} a^{n-2}b^2+\dots +\dbinom{n}{n-1} a^{1}b^{n-1}+\dbinom{n}{n}b^n \nonumber \]

    Usando el símbolo de suma, podemos escribir esto en breve:

    \[\boxed{(a+b)^n=\sum_{r=0}^n \dbinom{n}{r} \cdot a^{n-r} \cdot b^{r}} \]

    Ejemplo\(\PageIndex{4}\)

    Ampliar\((a+b)^5\).

    Solución

    \[\begin{aligned} (a+b)^5 &=\dbinom{5}{0} a^5+\dbinom{5}{1} a^{4}b^1+\dbinom{5}{2} a^{3}b^2 +\dbinom{5}{3} a^{2}b^{3}+\dbinom{5}{4} a^1b^{4}+\dbinom{5}{5}b^5 \\ &= a^5+5 a^4b+10 a^3b^2+10 a^2b^3+5ab^4+b^5\end{aligned} \nonumber \]

    This page titled 25.1: El Teorema Binomial is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Thomas Tradler and Holly Carley (New York City College of Technology at CUNY Academic Works) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.