1.4: Las mediciones
- Page ID
- 1796
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Explicar el proceso de la medición.
- Identificar las tres partes básicas de una cantidad.
- Describir las propiedades y unidades de longitud, masa, volumen, densidad, temperatura y tiempo
- Realizar cálculos y conversiones de unidades básicas en la métrica y otros sistemas de unidades
Las mediciones dan la información macroscópica que es la base de la mayoría de las hipótesis, teorías y leyes que describen el comportamiento de la materia y la energía tanto en el dominio macroscópico como en el dominio microscópico de la química. Cada medición proporciona tres tipos de información: el tamaño o la magnitud de la medición (un número); un estándar de comparación para la medida (una unidad); y una indicación de la incertidumbre de la medida. Mientras que el número y la unidad se representan explícitamente cuando se escribe una cantidad, la incertidumbre es un aspecto del resultado de la medición que se representa de manera más implícita y se explicará más adelante.
El número en la medición se puede representar de diferentes maneras, incluyendo la forma decimal y la notación científica. Por ejemplo, el peso máximo de despegue de un avión Boeing 777-200ER es de 298,000 kilogramos, que también se puede escribir como 2.98 \(\times\) 105 kg. La masa promedio del mosquito es de aproximadamente 0.0000025 kilogramos, que se puede escribir como 2.5\(\times\) 10-6 kg.
Las unidades, como litros, libras y centímetros, son estándares de comparación para las mediciones. Cuando compramos una botella de refresco de dos litros, esperamos que el volumen de la bebida se haya medido, para que sea dos veces más grande que el volumen que todos aceptan que sea un 1 litro. La carne que se usa para preparar una hamburguesa de 0.25 libras se mide, por lo que pesa un cuarto hasta 1 libra. Sin unidades, un número puede ser sin sentido, confuso o posiblemente mortal. Supongamos que un médico prescribe fenobarbital para controlar las convulsiones de un paciente y establece una dosis de "100" sin especificar unidades. Esto no solo será confuso para el profesional médico que administra la dosis, sino que las consecuencias pueden ser graves: 100 mg administrados tres veces al día pueden ser efectivos como anticonvulsivos, sino que una dosis única de 100 g es más de 10 veces la cantidad letal.
Por lo general, informamos los resultados de las mediciones científicas en unidades SI, una versión actualizada del sistema métrico, utilizando las unidades enumeradas en la Tabla \(\PageIndex{1}\). Otras unidades pueden derivarse de estas unidades base. Los estándares para estas unidades están fijados por acuerdo internacional, y se denominan Sistema Internacional de Unidades o Unidades SI (del francés, Système International d’Unités). Las unidades SI se han utilizadas por el Instituto Nacional de Estándares y Tecnología (NIST) de los Estados Unidos desde el año1964.
| Propiedad Medida | Nombre de la Unidad | Unidad de Símbolos |
|---|---|---|
| longitud | metro | m |
| masa | kilogramo | kg |
| tiempo | segundo | s |
| temperatura | kelvin | K |
| corriente eléctrica | amperio | A |
| cantidad de sustancia | mol | mol |
| intensidad luminosa | candela | cd |
A veces usamos unidades que son fracciones o múltiplos de una unidad base. El helado se vende en cuartos de galón (una unidad base que no es de SI), pintas (0.5 cuartos de galón) o galones (4 cuartos de galón). También usamos fracciones o múltiplos de unidades en el sistema SI, pero estas fracciones o múltiplos son siempre potencias de 10. Las unidades SI fraccionales o múltiples se nombran usando un prefijo y el nombre de la unidad base. Por ejemplo, una longitud de 1000 metros también se denomina kilómetro porque el prefijo kilo significa "mil", que en notación científica es 103 (1 kilómetro = 1000 m = 103 m). Los prefijos utilizados y las potencias a las que se elevan 10 se enumeran en la Tabla \(\PageIndex{2}\).
| Prefijo | Símbolo | Factor | Ejemplo |
|---|---|---|---|
| femto | f | 10−15 | 1 femtosegundo (fs) = 1 \(\times\) 10−15 s (0.000000000000001 s) |
| pico | p | 10−12 | 1 picometro(pm) = 1 \(\times\) 10−12 m (0.000000000001 m) |
| nano | n | 10−9 | 4 nanogramos (ng) = 4 \(\times\) 10−9 g (0.000000004 g) |
| micro | µ | 10−6 | 1 microlitro (μL) = 1 \(\times\) 10−6 L (0.000001 L) |
| mili | m | 10−3 | 2 milimoles (mmol) = 2 \(\times\) 10−3 mol (0.002 mol) |
| centi | c | 10−2 | 7 centímetros (cm) = 7 \(\times\) 10−2 m (0.07 m) |
| deci | d | 10−1 | 1 decilitro (dL) = 1 \(\times\) 10−1 L (0.1 L ) |
| kilo | k | 103 | 1 kilómetro (km) = 1 \(\times\) 103 m (1000 m) |
| mega | M | 106 | 3 megahertzios (MHz) = 3 \(\times\) 106 Hz (3,000,000 Hz) |
| giga | G | 109 | 8 giga años(Gyr) = 8 \(\times\) 109 yr (8,000,000,000 Gyr) |
| tera | T | 1012 | 5 Tera vatios (TW) = 5 \(\times\) 1012 W (5,000,000,000,000 W) |
Las unidades base del SI
Las unidades iniciales del sistema métrico, que eventualmente evolucionaron hacia el sistema SI, se establecieron en Francia durante la Revolución Francesa. Los estándares originales para el medidor y el kilogramo fueron adoptados allí en 1799 y eventualmente por otros países. Esta sección presenta cuatro de las unidades base del SI que se usan comúnmente en química. Otras unidades del SI serán introducidas en capítulos que siguen.
La longitud
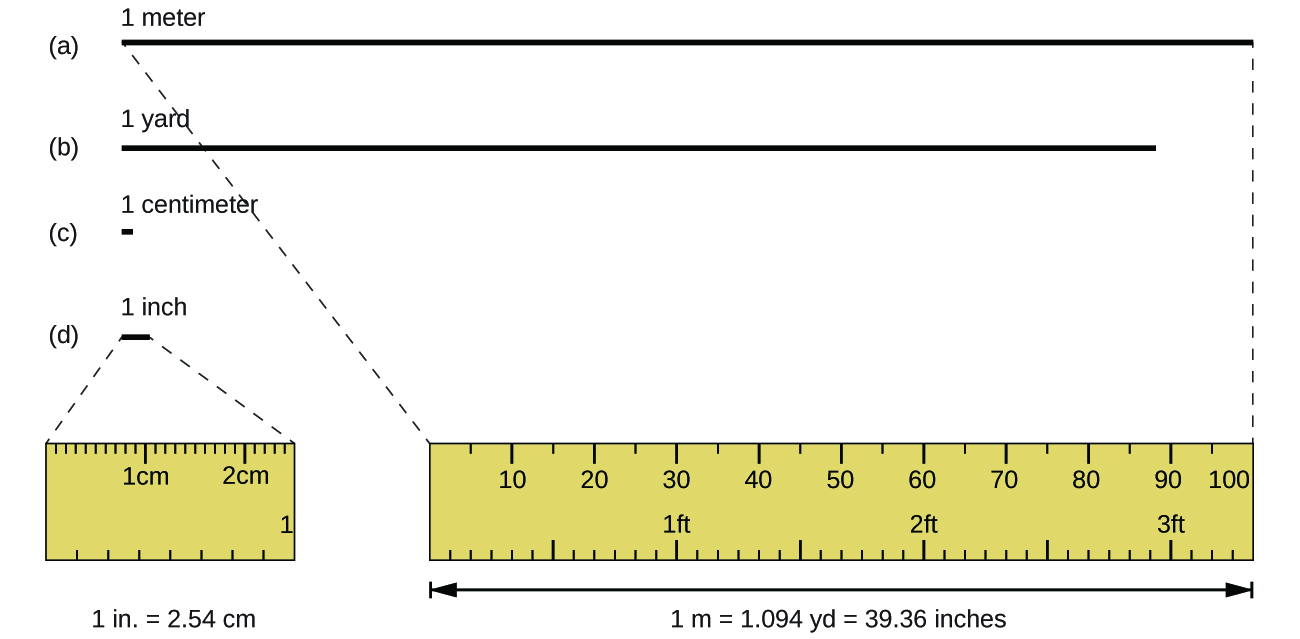
La unidad estándar de longitud en el SI y en los sistemas métricos originales es el metro (m). Un metro se especificó originalmente como 1/10,000,000 de la distancia desde el Polo Norte hasta el ecuador. Ahora se define como la distancia que la luz en el vacío viaja en 1/299,792,458 de segundo. Un metro es aproximadamente 3 pulgadas más largo que una yarda (Figura \(\PageIndex{1}\)); Un metro mide aproximadamente 39.37 pulgadas o 1.094 yardas. A menudo, las distancias más largas se reportan en kilómetros (1 km = 1000 m = 103 m), mientras que las distancias más cortas se pueden reportar en centímetros (1 cm = 0.01 m = 10-2 m) o milímetros (1 mm = 0.001 m = 103 metro).
La masa
La unidad estándar de masa en el sistema SI es el kilogramo (kg). Un kilogramo se definió originalmente como la masa de un litro de agua (un cubo de agua con una longitud de borde de exactamente 0.1 metros). Ahora está definido por un cierto cilindro de aleación de platino-iridio, que se mantiene en Francia (Figura 1.4.2). Cualquier objeto con la misma masa que sea cilindro, se dice que tiene una masa de 1 kilogramo. Un kilogramo es de aproximadamente 2.2 libras. El gramo (g) es exactamente igual a 1/1000 de la masa del kilogramo (10-3 kg).

La temperatura
La temperatura es una propiedad intensiva. La unidad de temperatura SI es el kelvin (K). La convención IUPAC es usar kelvin (todo en minúsculas) para la palabra, K (mayúscula) para el símbolo de la unidad, y ni la palabra "grado" ni el símbolo de grado (°). El grado Celsius (° C) también se permite en el sistema SI, con la palabra "grado" y el símbolo de grado utilizado para las mediciones de Celsius. Los grados centígrados son de la misma magnitud que los de kelvin, pero las dos escalas colocan sus ceros en diferentes lugares. El agua se congela a 273.15 K (0 ° C) y hierve a 373.15 K (100 ° C) por definición, y la temperatura temperatura normal del cuerpo humano es de aproximadamente 310 K (37 ° C). La conversión entre estas dos unidades y la escala Fahrenheit se discutirá más adelante en este capítulo.
El tiempo
La unidad de tiempo del SI es el segundo (s). Los intervalos de tiempo pequeños y grandes se pueden expresar con los prefijos apropiados; por ejemplo, 3 microsegundos = 0.000003 s = 3 \(\times\) 10-6 y 5 mega segundos = 5,000,000 s = 5 \(\times\) 106 s. Alternativamente, se pueden utilizar horas, días y años.
Las unidades derivadas del SI
Podemos derivar muchas unidades de las siete unidades base SI. Por ejemplo, podemos usar la unidad base de longitud para definir una unidad de volumen, y las unidades base de masa y longitud para definir una unidad de densidad.
El volumen
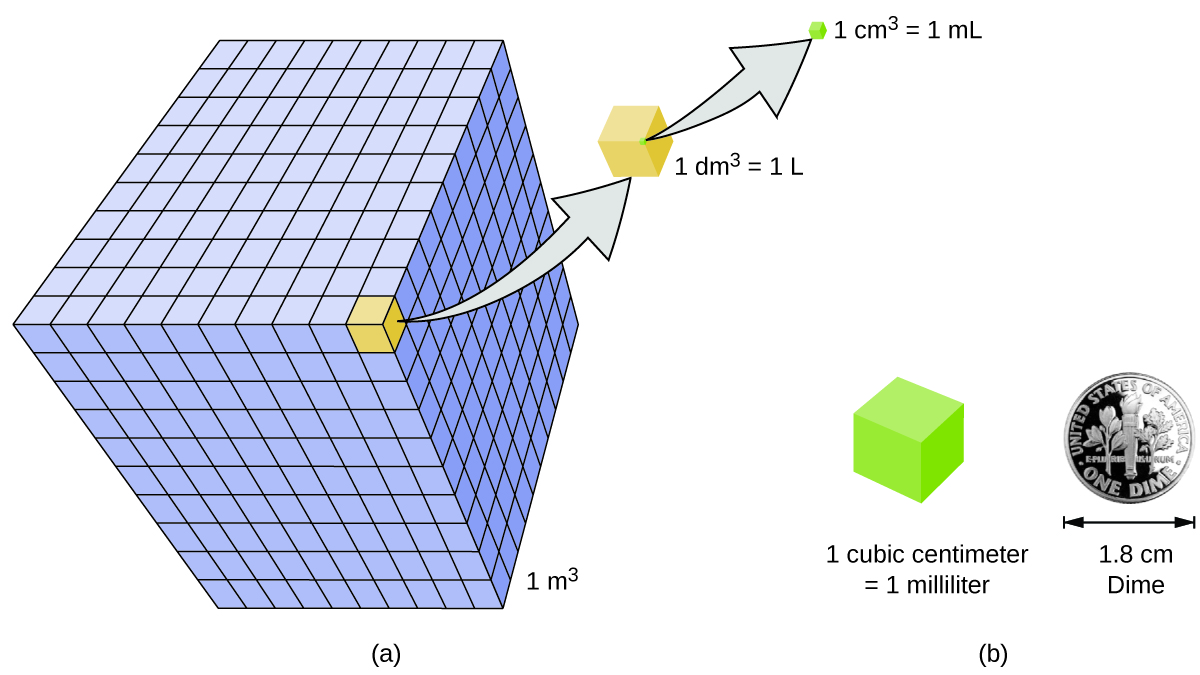
El volumen es la medida de la cantidad de espacio ocupado por un objeto. La unidad de volumen SI estándar se define por la unidad base de longitud (Figura \(\PageIndex{3}\)). El volumen estándar es un metro cúbico (m3), un cubo con una longitud de borde de exactamente un metro. Para dispensar un metro cúbico de agua, podríamos construir una caja cúbica con longitudes de borde de exactamente un metro. Esta caja podría contener un metro cúbico de agua o cualquier otra sustancia.
Una unidad de volumen más utilizada se deriva del decímetro (0.1 m, o 10 cm). Un cubo con longitudes de borde de exactamente un decímetro contiene un volumen de un decímetro cúbico (dm3). Un litro (L) es el nombre más común para el decímetro cúbico. Un litro es alrededor de 1.06 cuartos de galón. Un centímetro cúbico (cm3) es el volumen de un cubo con una longitud de borde de exactamente un centímetro. La abreviatura cc (para centímetro cúbico) a menudo es utilizada por profesionales de la salud. Un centímetro cúbico también se llama mililitro (mL) y es 1/1000 de un litro.
La densidad
Utilizamos la masa y el volumen de una sustancia para determinar su densidad. Así, las unidades de densidad están definidas por las unidades base de masa y longitud.
La densidad de una sustancia es la relación entre la masa de una muestra de la sustancia y su volumen. La unidad SI para densidad es el kilogramo por metro cúbico (kg/m3). Sin embargo, para muchas situaciones, esto es una unidad inconveniente, y con frecuencia usamos gramos por centímetro cúbico (g/cm3) para las densidades de sólidos y líquidos, y gramos por litro (g/L) para gases. Aunque hay excepciones, la mayoría de los líquidos y sólidos tienen densidades que oscilan entre aproximadamente 0.7 g/cm3 (la densidad de la gasolina) y 19 g/cm3 (la densidad del oro). La densidad del aire es de aproximadamente 1.2 g /L. La tabla \(\PageIndex{3}\) muestra las densidades de algunas sustancias comunes.
| Sólidos | Líquidos | Gases (a 25 °C y 1 atm) |
|---|---|---|
| hielo (a 0 °C) 0.92 g/cm3 | agua 1.0 g/cm3 | aire seco 1.20 g/L |
| roble (madera) 0.60–0.90 g/cm3 | etanol 0.79 g/cm3 | oxígeno 1.31 g/L |
| hierro 7.9 g/cm3 | acetona 0.79 g/cm3 | nitrógeno 1.14 g/L |
| cobre 9.0 g/cm3 | glicerina 1.26 g/cm3 | dióxido de carbono 1.80 g/L |
| plomo11.3 g/cm3 | aceite de oliva 0.92 g/cm3 | helio 0.16 g/L |
| plata 10.5 g/cm3 | gasolina 0.70–0.77 g/cm3 | neon 0.83 g/L |
| oro 19.3 g/cm3 | mercurio 13.6 g/cm3 | radón 9.1 g/L |
Aunque hay muchas maneras de determinar la densidad de un objeto, tal vez el método más sencillo consiste en encontrando la masa y el volumen del objeto a diferentes tiempos, y luego dividir la masa de la muestra por su volumen. En el siguiente ejemplo, la masa se encuentra directamente por pesando la, pero el volumen se encuentra indirectamente a través de mediciones de longitud.
\[\mathrm{density=\dfrac{mass}{volume}}\]
Ejemplo \(\PageIndex{1}\)
El cálculo de la densidad del oro- ladrillos, barras y monedas, han sido una forma de dinero durante siglos. Con el fin de estafar a la gente para que pague por un ladrillo de oro sin invertir realmente en un ladrillo de oro, la gente ha considerado llenar los centros de ladrillos huecos de oro con el fin de engañar a los compradores para que piensen que todo el ladrillo es oro. No funciona: el plomo es una sustancia densa, pero su densidad no es tan grande como la del oro, 19.3 g/cm3. ¿Cuál es la densidad del plomo si un cubo de plomo tiene una longitud de borde de 2.00 cm y una masa de 90.7 g?
Solución
La densidad de una sustancia se puede calcular dividiendo su masa por su volumen. El volumen de un cubo se calcula al cubicar la longitud del borde.
\[\mathrm{volume\: of\: lead\: cube=2.00\: cm\times2.00\: cm\times2.00\: cm=8.00\: cm^3} \nonumber\]
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{90.7\: g}{8.00\: cm^3}=\dfrac{11.3\: g}{1.00\: cm^3}=11.3\: g/cm^3} \nonumber\]
(We will discuss the reason for rounding to the first decimal place in the next section.)
EJerCiCIo \(\PageIndex{1}\)
a. A tres lugares decimales, ¿Cuál es el volumen de un cubo (cm3) con una longitud de borde de 0.843 cm?
b. Si el cubo en la parte (a) es de cobre y tiene una masa de 5.34 g, ¿Cuál es la densidad del cobre a dos lugares decimales?
- Respuesta a
-
0.599 cm3;
- Respuesta b
-
8.91 g/cm3
EJemplo \(\PageIndex{2}\): UTILIZANDO EL DESPLAZAMIENTO DEL AGUA PARA DETERMINAR LA DENSIDAD
Esta Simulación de PhET Ilustra otra forma de determinar la densidad, utilizando el desplazamiento del agua. Determine la densidad de los bloques rojos y amarillos.
Solución
Cuando abre la simulación de densidad y selecciona Misma Masa, puede elegir entre varios bloques de colores de 5.00 kg que puede colocar en un tanque que contiene 100.00 L de agua. El bloque amarillo flota (es menos denso que el agua) y el nivel del agua sube a 105.00 L. Mientras flota, el bloque amarillo desplaza 5.00 L de agua, una cantidad igual al peso del bloque. El bloque rojo se hunde (es más denso que el agua, que tiene una densidad = 1.00 kg / L) y el nivel del agua se eleva a 101.25 L.
Por lo tanto, el bloque rojo desplaza 1.25 L de agua, una cantidad igual al volumen del bloque. La densidad del bloque rojo es:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{1.25\: L}=4.00\: kg/L}\]
Tenga en cuenta que ya que el bloque amarillo no está completamente sumergido, no puede determinar su densidad con esta información. Pero si mantiene el bloque amarillo en la parte inferior del tanque, el nivel del agua aumenta a 110.00 L, lo que significa que ahora desplaza a 10.00 L de agua, y se puede encontrar su densidad:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{5.00\: kg}{10.00\: L}=0.500\: kg/L}\]
Ejercicio \(\PageIndex{1}\)
Retire todos los bloques del agua y agregue el bloque verde al tanque de agua, colocándolo aproximadamente en el centro del tanque. Determine la densidad del bloque verde.
- Respuesta
-
2.00 kg/L
Resumen
Las mediciones dan información cuantitativa que es crítica en el estudio y la práctica de la química. Cada medida tiene una cantidad, una unidad para comparación y una incertidumbre. Las mediciones se pueden representar en notación decimal o científica. Los científicos utilizan principalmente el SI (Sistema Internacional) o los sistemas métricos. Usamos unidades base SI como metros, segundos y kilogramos, así como unidades derivadas, como litros (para volumen) y g / cm3 (para densidad). En muchos casos, nos parece conveniente utilizar prefijos de unidad que produzcan unidades fraccionarias y múltiples, como microsegundos (10-6 segundos) y megahercios (106 hertzios), respectivamente.
Ecuaciones Claves
- \(\mathrm{density=\dfrac{mass}{volume}}\)
Glosario
- Celsius (°C)
- Unidad de temperatura; El agua se congela a 0 ° C y hierve a 100 ° C en esta escala.
- centímetro cúbico(cm3 or cc)
- Volumen de un cubo con una longitud de borde de exactamente 1 cm.
- metro cúbico(m3)
- Unidad de volumen SI.
- densidad
- Relación de masa a volumen para una sustancia u objeto.
- kelvin (K)
- Unidad de temperatura SI; 273.15 K = 0 ºC
- kilogramo(kg)
- Unidad de masa SI estándar; 1 kg = aproximadamente 2.2 libras.
- longitud
- Medida de una dimensión de un objeto.
- litro (L)
- (también, decímetro cúbico) Unidad de volumen; 1 L = 1,000 cm3
- metro (m)
- Unidad métrica estándar y SI de longitud; 1 m = aproximadamente 1.094 yardas.
- mililitro (mL)
- 1 / 1,000 de un litro; igual a 1 cm3
- segundo (s)
- Unidad de tiempo SI.
- Unidades SI (Sistema Internacional de Unidades)
- Normas fijadas por acuerdo internacional en el Sistema Internacional de Unidades(Le Système International d’Unités).
- unidad
- Estándar de comparación para mediciones.
- volumen
- Cantidad de espacio ocupado por un objeto.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


