3.2: La determinación de las fórmulas empíricas y moleculares
- Page ID
- 1812
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Calcular la composición porcentual de un compuesto
- Determinar la fórmula empírica de un compuesto.
- Determinar la fórmula molecular de un compuesto.
En la sección anterior, discutimos la relación entre la masa masiva de una sustancia y el número de átomos o moléculas que contiene (moles). Sabiendo la fórmula química de la sustancia, pudimos determinar la cantidad de la sustancia (moles) de su masa y viceversa. ¿Pero qué pasa si la fórmula química de una sustancia no se sabe? En esta sección, exploraremos cómo aplicar estos mismos principios para derivar las fórmulas químicas de sustancias desconocidas, hacemos esto a partir de mediciones de masa experimentales.
La composición porcentual
La composición elemental de un compuesto define su identidad química, y las fórmulas químicas son la forma más concisa de representar esta composición elemental. Cuando se desconoce la fórmula de un compuesto, la medición de la masa de cada uno de sus elementos constitutivos es a veces el primer paso en el proceso de la determinación experimental de la fórmula. Los resultados de estas mediciones permiten el cálculo de la composición porcentual del compuesto, definida como el porcentaje de masa de cada elemento en el compuesto. Por ejemplo, considere un compuesto gaseoso que contiene solamente carbono e hidrógeno. El porcentaje de composición de este compuesto se puede representar en la siguiente manera:
\[\mathrm{\%H=\dfrac{mass\: H}{mass\: compound}\times100\%}\]
Si el análisis de una muestra de 10,0 g de este gas indica que contiene 2,5 g de H y 7,5 g de C, el porcentaje de composición se calcularía a ser 25% de H y 75% de C:
\[\mathrm{\%H=\dfrac{2.5\:g\: H}{10.0\:g\: compound}\times100\%=25\%}\]
\[\mathrm{\%C=\dfrac{7.5\:g\: C}{10.0\:g\: compound}\times100\%=75\%}\]
Ejemplo \(\PageIndex{1}\): CÁLCULO Del porcentaje de COMPOSICIÓN
El análisis de una muestra de 12,04 g de un compuesto líquido que contenía carbono, hidrógeno y nitrógeno mostró que estaba hecho de 7.34 g C, 1.85 g H y 2.85 g N. ¿Cuál es la composición porcentual de este compuesto?
Solución
Para calcular la composición porcentual, dividimos la masa experimentalmente de cada elemento por la masa total del compuesto y luego lo convertimos a un porcentaje:
\[\mathrm{\%C=\dfrac{7.34\:g\: C}{12.04\:g\: compound}\times100\%=61.0\%} \nonumber\]
\[\mathrm{\%H=\dfrac{1.85\:g\: H}{12.04\:g\: compound}\times100\%=15.4\%} \nonumber\]
\[\mathrm{\%N=\dfrac{2.85\:g\: N}{12.04\:g\: compound}\times100\%=23.7\%} \nonumber\]
Los resultados del análisis indican que el compuesto es 61.0% C, 15.4% H y 23.7% N en masa.
Ejercicio \(\PageIndex{1}\)
Una muestra de 24,81 g de un compuesto gaseoso que contiene solamente carbono, oxígeno y cloro contiene 3,01 g C, 4,00 g O, y 17,81 g Cl. ¿Cuál es la composición porcentual de este compuesto?
- Respuesta
-
12,1% C, 16,1% O, 71,8% Cl
Determinando el porcentaje de composición de la fórmula de masa
El porcentaje de composición también es útil para evaluar la abundancia relativa de un elemento dado en diferentes compuestos de fórmulas conocidas. Por ejemplo, considere los fertilizantes comunes que contienen nitrógeno amoníaco (NH3), nitrato de amonio (NH4NO3), y urea (CH4N2O). El elemento nitrógeno es el ingrediente activo en fertilizantes de agricultura, por eso el porcentaje de masa de nitrógeno en el compuesto es una preocupación práctica y económica para los consumidores que eligen entre estos fertilizantes. Para estas aplicaciones, el porcentaje de composición de un compuesto se deriva fácilmente de su masa de fórmula y las masas atómicas de sus elementos constituyentes. Una molécula de NH3 contiene un átomo de N que pesa 14,01 amu y tres átomos de H que pesan un total de (3 × 1,008 amu) = 3,024 amu. Por eso, la fórmula de amoníaco es (14,01 amu + 3,024 amu) = 17,03 amu, y su composición porcentual es:
\[\mathrm{\%N=\dfrac{14.01\:amu\: N}{17.03\:amu\:NH_3}\times100\%=82.27\%}\]
\[\mathrm{\%H=\dfrac{3.024\:amu\: N}{17.03\:amu\:NH_3}\times100\%=17.76\%}\]
Este mismo enfoque se puede tomar cuando se consideran un par de moléculas, una docena de moléculas, o un mol de moléculas, etc. La última cantidad es más conveniente y simplemente involucraría el uso de masas molares en lugar de masas atómicas y de fórmula, como se demuestra en el Ejemplo (\PageIndex{2}\). Siempre que sabemos la fórmula química de la sustancia en cuestión, podemos fácilmente obtener el porcentaje de composición de la fórmula masa o masa molar.
Ejemplo \(\PageIndex{2}\): DETERMINANDO el porcentaje de COMPOSICIÓN DE UNA FÓRMULA MOLECULAR
La aspirina es un compuesto con la fórmula molecular C9H8O4. ¿Cuál es su composición porcentual?
Solución
Para calcular el porcentaje de composición, necesitamos saber las masas de C,H, y O en una masa conocida de C9H8O4. Es conveniente considerar 1 mol de C9H8O4 y usar su masa molar (180,159 g/mol, determinada de su fórmula química) para calcular los porcentajes de cada uno de sus elementos:
\[\begin{align*}
\%\ce C&=\mathrm{\dfrac{9\:mol\: C\times molar\: mass\: C}{molar\: mass\:\ce{C9H18O4}}\times100=\dfrac{9\times12.01\:g/mol} \nonumber{180.159\:g/mol}\times100=\dfrac{108.09\:g/mol}{180.159\:g/mol}\times100} \nonumber\\
\%\ce C&=\mathrm{60.00\,\%\,C} \nonumber
\end{align*}\]
\[\begin{align*}
\%\ce H&=\mathrm{\dfrac{8\:mol\: H\times molar\: mass\: H}{molar\: mass\:\ce{C9H18O4}}\times 100=\dfrac{8\times 1.008\:g/mol} \nonumber {180.159\:g/mol}\times 100=\dfrac{8.064\:g/mol}{180.159\:g/mol}\times 100} \nonumber\\
\%\ce H&=4.476\,\%\,\ce H\nonumber
\end{align*}\]
\[\begin{align*}
\%\ce O&=\mathrm{\dfrac{4\:mol\: O\times molar\: mass\: O}{molar\: mass\: \ce{C9H18O4}}\times 100=\dfrac{4\times 16.00\:g/mol} \nonumber{180.159\:g/mol}\times 100=\dfrac{64.00\:g/mol}{180.159\:g/mol}\times 100} \nonumber \\
\%\ce O&=35.52\% \nonumber
\end{align*}\]
Tenga en cuenta que estos porcentajes suman a 100.00% cuando se redondean adecuadamente.
Ejercicio \(\PageIndex{2}\)
A tres dígitos significativos, ¿Cuál es el porcentaje de masa de hierro en el compuesto? \(Fe_2O_3\)?
- Respuesta
-
69,9% Fe
La determinación de fórmulas empíricas
Como se mencionó antes, el enfoque más común para determinar la fórmula química de un compuesto es primero medir las masas de sus elementos constituyentes. Sin embargo, debemos tener en cuenta que las fórmulas químicas representan los números relativos, no las masas, de los átomos en la sustancia. Por lo tanto, cualquier dato derivado experimentalmente de masa se debe usar para derivar los números correspondientes de átomos en el compuesto. Para lograr esto, podemos usar masas molares para convertir la masa de cada elemento a un número de moles. Luego, consideramos los moles de cada elemento en relación uno con el otro, convirtiendo estos números a una proporción de números enteros que se pueden usar para derivar la fórmula empírica de la sustancia. Considere una muestra de compuesto determinado a contener 1,71 g C y 0,287 g H. Los números correspondientes de átomos (en moles) son:
\[\mathrm{1.71\:g\: C\times \dfrac{1\:mol\: C}{12.01\:g\: C}=0.142\:mol\: C}\]
\[\mathrm{0.287\:g\: H\times \dfrac{1\:mol\: H}{1.008\:g\: H}=0.284\:mol\: H}\]
Por lo tanto, podemos representar este compuesto con la fórmula C0.142H0.284. Por supuesto, según la convención aceptada, las fórmulas contienen subíndices de números enteros, que se pueden lograr con dividiendo cada subíndice por el subíndice más pequeño:
\[\ce C_{\Large{\frac{0.142}{0.142}}}\:\ce H_{\Large{\frac{0.284}{0.142}}}\ce{\:or\:CH2}\]
(Recuerde que los subíndices de "1" no se escriben, sino que se asumen si no hay otro número presente).
La fórmula empírica para este compuesto es CH2. Esta puede ser, o no ser la fórmula molecular del compuesto; sin embargo, necesitaríamos información adicional para hacer esa determinación (como veremos más adelante en esta sección).
Considere como otro ejemplo una muestra de un compuesto que se determina a contener 5,31 g Cl y 8,40 g O. Siguiendo el mismo enfoque se obtiene una fórmula empírica tentativa de:
\[\mathrm{Cl_{0.150}O_{0.525}=Cl_{\Large{\frac{0.150}{0.150}}}\: O_{\Large{\frac{0.525}{0.150}}}=ClO_{3.5}}\]
En este caso, dividiendo por el subíndice más pequeño todavía nos deja un subíndice decimal en la fórmula empírica. Para convertir esto a un número entero, debemos multiplicar cada uno de los subíndices por dos, reteniendo la misma proporción de átomos y obteniendo Cl2O7 como la fórmula empírica final.
Procedimiento
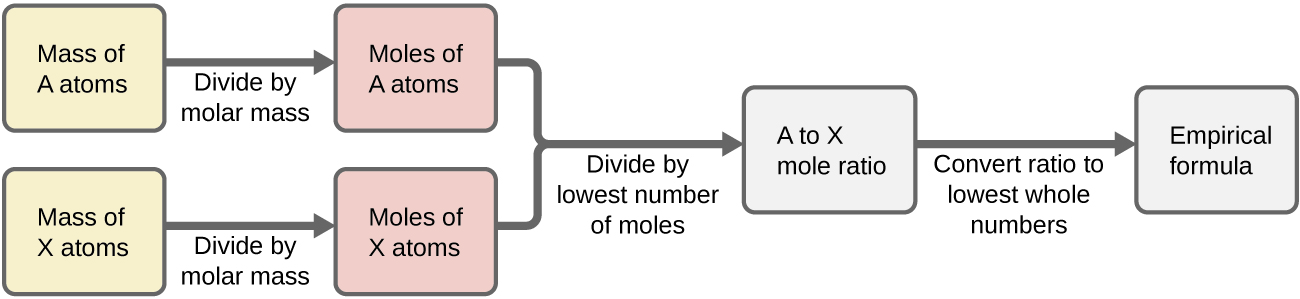
En resumen, las fórmulas empíricas se derivan de masas de elementos medidas experimentalmente a través de:
1.Derivando el número de moles de cada elemento a partir de su masa.
2.Dividiendo la cantidad molar de cada elemento por la cantidad molar más pequeña para producir subíndices tentativos para una fórmula empírica.
3.Multiplicando todos los coeficientes por un número entero, si es necesario, para asegurar que se obtenga la proporción más pequeña de subíndices de números enteros
Figura \(\PageIndex{1}\) enseña este procedimiento en un diagrama de flujo para una sustancia conteniendo los elementos A y X.
Ejemplo \(\PageIndex{3}\):Determinando la Fórmula Empírica a partir de Masas de Elementos
Una muestra de la mineral hematita negra (Figura \(\PageIndex{2}\)), un óxido de hierro presente en muchos minerales de hierro, contiene 34,97 g de hierro y 15,03 g de oxígeno. ¿Cuál es la fórmula empírica de la hematita?

Solución
Para este problema, se nos da la masa en gramos de cada elemento. Comience por encontrando el número de moles de cada uno:
\[\begin{align*}
\mathrm{34.97\:g\: Fe\left(\dfrac{mol\: Fe}{55.85\:g}\right)}&=\mathrm{0.6261\:mol\: Fe}\nonumber\\ \nonumber\\
\mathrm{15.03\:g\: O\left(\dfrac{mol\: O}{16.00\:g}\right)}&=\mathrm{0.9394\:mol\: O} \nonumber
\end{align*}\]
Después, obtenga la relación molar de hierro a oxígeno dividiendo por el número menor de moles:
\[\mathrm{\dfrac{0.6261}{0.6261}=1.000\:mol\: Fe} \nonumber\]
\[\mathrm{\dfrac{0.9394}{0.6261}=1.500\:mol\: O} \nonumber\]
La relación es de 1.000 mol de hierro a 1.500 moles de oxígeno (Fe1O1.5). Finalmente, multiplique la proporción por dos para obtener los subíndices de números enteros más pequeños posibles mientras mantiene la proporción correcta de hierro a oxígeno:
\[\mathrm{2(Fe_1O_{1.5})=Fe_2O_3}\nonumber\]
La fórmula empírica es \(Fe_2O_3\).
Ejercicio \(\PageIndex{3}\)
¿Cuál es la fórmula empírica de un compuesto si una muestra contiene 0,130 g de nitrógeno y 0,370 g de oxígeno?
- Respuesta
-
\(N_2O_5\)
Vídeo \(\PageIndex{1}\): En este breve video clip se presentan ejemplos adicionales que ilustran la derivación de fórmulas empíricas.
Derivando fórmulas empíricas de composición porcentual
Finalmente, con respecto a la derivación de fórmulas empíricas, considere los casos cuando la composición porcentual de un compuesto está disponible en lugar de las masas absolutas de los elementos en el compuesto. En estos casos, el porcentaje de composición se puede usar para calcular las masas de elementos presentes en cualquier masa conveniente de compuesto; estas masas se pueden usar para derivar la fórmula empírica de la manera usual.
Ejemplo \(\PageIndex{4}\): Determinando una Fórmula Empírica del Porcentaje de Composición
La fermentación de bacteria del grano para producir etanol, forma un gas con una composición porcentual de 27,29% C y 72,71% O (Figura \(\PageIndex{3}\)). ¿Cuál es la fórmula empírica de este gas?

Solución
Ya que la escala para porcentajes es 100, es más conveniente calcular la masa de los elementos presentes en una muestra que pesa 100 g. El cálculo es "más conveniente" porque, según la definición de composición porcentual, la masa de un elemento dado en gramos es numéricamente equivalente al porcentaje de masa del elemento. Esta equivalencia numérica se viene de la definición de la unidad de "porcentaje", cuyo nombre se deriva de la frase en latín por centum que significa "por cien". Considerando esta definición, los porcentajes de masa dados se pueden expresar más convenientemente como fracciones:
\[\begin{align*}
27.29\,\%\,\ce C&=\mathrm{\dfrac{27.29\:g\: C}{100\:g\: compound}}\nonumber \\ \nonumber \\
72.71\,\%\,\ce O&=\mathrm{\dfrac{72.71\:g\: O}{100\:g\: compound}} \nonumber
\end{align*}\]
Las cantidades molares de carbono y de hidrógeno en una muestra de 100 g se calculan dividiendo la masa de cada elemento por su masa molar:
\[\begin{align*}
\mathrm{27.29\:g\: C\left(\dfrac{mol\: C}{12.01\:g}\right)}&=\mathrm{2.272\:mol\: C} \nonumber \\ \nonumber \\
\mathrm{72.71\:g\: O\left(\dfrac{mol\: O}{16.00\:g}\right)}&=\mathrm{4.544\:mol\: O} \nonumber
\end{align*}\]
Los coeficientes para la fórmula empírica tentativa se derivan al dividir cada cantidad molar por la menor de las dos cantidades:
\[\mathrm{\dfrac{2.272\:mol\: C}{2.272}=1} \nonumber\]
\[\mathrm{\dfrac{4.544\:mol\: O}{2.272}=2} \nonumber\]
La relación resultante es de un carbono a dos átomos de oxígeno, la fórmula empírica es CO2.
Ejercicio \(\PageIndex{4}\)
¿ Cuál es la fórmula empírica de un compuesto conteniendo 40,0% C, 6,71% H, y 53,28% O?
- Respuesta
-
\(CH_2O\)
La derivación de fórmulas moleculares
Recuerde que las fórmulas empíricas son símbolos representando los números relativos de los elementos de un compuesto. Determinando los números absolutos de los átomos que componen una sola molécula de un compuesto covalente, requiere el conocimiento de su fórmula empírica y de su masa molecular o masa molar. Estas cantidades se pueden determinar experimentalmente por varias técnicas de medición. Por ejemplo, la masa molecular a veces se deriva del espectro de masas (vea la discusión de esta técnica en el capítulo anterior sobre átomos y moléculas). La masa molar se puede medir por varios métodos experimentales, muchos de los cuales se introducirán en capítulos que siguen este texto.
Las fórmulas moleculares se obtienen comparando la masa molecular o masa molar del compuesto con su masa de fórmula empírica. Como su nombre indica, una masa de fórmula empírica es la suma de las masas atómicas promedio de todos los átomos representados en la fórmula empírica. Si conocemos la masa molecular (o molar) de la sustancia, podemos dividirla por la masa de fórmula empírica para identificar el número de unidades por molécula de fórmula empírica, que designamos como n:
\[\mathrm{\dfrac{molecular\: or\: molar\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}{empirical\: formula\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}= \mathit n\: formula\: units/molecule}\]
La fórmula molecular se obtiene por multiplicando cada subíndice en la fórmula empírica por n, como se muestra en la fórmula empírica genérica AxBy:
\[\mathrm{(A_xB_y)_n=A_{nx}B_{nx}}\]
Por ejemplo, considere un compuesto covalente cuya fórmula empírica se determina a ser CH2O. La masa de fórmula empírica para este compuesto es de aproximadamente 30 amu (la suma de 12 amu para un átomo de C, 2 amu para dos átomos de H, y 16 amu para un átomo de O). Si la masa molecular del compuesto se determina a ser 180 amu, esto indica que las moléculas de este compuesto contienen seis veces el número de átomos representados en la fórmula empírica:
\[\mathrm{\dfrac{180\:amu/molecule}{30\:\dfrac{amu}{formula\: unit}}=6\:formula\: units/molecule}\]
Las moléculas de este compuesto se representan por fórmulas moleculares cuyos subíndices son seis veces más grandes que los de la fórmula empírica:
\[\ce{(CH2O)6}=\ce{C6H12O6}\]
Tenga en cuenta que este mismo enfoque se puede usar cuando se usa la masa molar (g/mol) en lugar de la masa molecular (amu) En este caso, estamos simplemente considerando un mol de unidades de fórmula empírica y moléculas, en lugar de unidades y moléculas individuales.
Ejemplo \(\PageIndex{5}\): DETERMINACIÓN DE LA FÓRMULA MOLECULAR PARA NICOTINA
La nicotina, un alcaloide en la familia de las plantas de hierba mora que es principalmente responsable para la naturaleza adictiva de los cigarrillos, contiene 74,02% C, 8,710% H y 17,27% N. Si 40,57 g de nicotina contiene 0,2500 mol de nicotina, ¿Cuál es la fórmula molecular?
Solución
La determinación de la fórmula molecular a partir de los datos dados requerirá la comparación de la masa de la fórmula empírica del compuesto con su masa molar. Como el primer paso, use la composición porcentual para derivar la fórmula empírica del compuesto. Suponiendo que sea conveniente, una muestra de nicotina de 100 g produce las siguientes cantidades molares de sus elementos:
\[\begin{alignat}{2}
&\mathrm{(74.02\:g\: C)\left(\dfrac{1\:mol\: C}{12.01\:g\: C}\right)}&&= \:\mathrm{6.163\:mol\: C}\\
&\mathrm{(8.710\:g\: H)\left(\dfrac{1\:mol\: H}{1.01\:g\: H}\right)}&&= \:\mathrm{8.624\:mol\: H}\\
&\mathrm{(17.27\:g\: N)\left(\dfrac{1\:mol\: N}{14.01\:g\: N}\right)}&&= \:\mathrm{1.233\:mol\: N}
\end{alignat}\]
Luego, calculamos las relaciones molares de estos elementos en relación con el elemento menos abundante, \(\ce{N}\).
\(6.163 \: \text{mol} \: \ce{C}\) / \(1.233 \: \text{mol} \: \ce{N}\) = 5
\(8.264 \: \text{mol} \: \ce{H}\) / \(1.233 \: \text{mol} \: \ce{N}\) = 7
\(1.233 \: \text{mol} \: \ce{N}\) / \(1.233\: \text{mol} \: \ce{N}\) = 1
1.233/1.233 = \(1.000 \: \text{mol} \: \ce{N}\)
6.163/1.233 = \(4.998 \: \text{mol} \: \ce{C}\)
8.624/1.233 = \(6.994 \: \text{mol} \: \ce{H}\)
Las relaciones molares de C a N y de H a N son adecuadamente cercanas a números enteros, por eso la fórmula empírica es C5H7N. La masa de la fórmula empírica para este compuesto es 81,13 amu/unidad de fórmula, o 81.13 g/mol de fórmula.
Calculamos la masa molar de nicotina a partir de la masa dada y la cantidad molar del compuesto.
\[\mathrm{\dfrac{40.57\:g\: nicotine}{0.2500\:mol\: nicotine}=\dfrac{162.3\:g}{mol}} \nonumber \]
Comparando la masa molar y la fórmula empírica de nicotina indica que cada molécula de nicotina contiene dos unidades de fórmula.
\[\mathrm{\dfrac{162.3\:g/mol}{81.13\:\dfrac{g}{formula\: unit}}=2\:formula\: units/molecule} \nonumber\]
Así, podemos derivar la fórmula molecular para la nicotina de la fórmula empírica multiplicando cada subíndice por dos.
\[\ce{(C5H7N)2}=\ce{C10H14N2} \nonumber\]
Ejercicio \(\PageIndex{5}\)
¿Cuál es la fórmula molecular de un compuesta con una composición porcentual de 49,47% C, 5,201% H, 28,84% N, y 16,48% O, y una masa molecular de 194,2 amu?
- Respuesta
-
C8H10N4O2
Resumen
La identidad química de una sustancia se define por los tipos y números relativos de átomos que componen sus entidades fundamentales (moléculas en el caso de compuestos covalentes, iones en el caso de compuestos iónicos). La composición porcentual de un compuesto da el porcentaje en masa de cada elemento en el compuesto, y a veces se determina experimentalmente y se usa para derivar la fórmula empírica del compuesto. La masa de fórmula empírica de un compuesto covalente se puede comparar con la masa molecular o masa molar del compuesto para obtener una fórmula molecular.
Ecuaciones Claves
- \(\mathrm{\%X=\dfrac{mass\: X}{mass\: compound}\times100\%}\)
- \(\mathrm{\dfrac{molecular\: or\: molar\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}{empirical\: formula\: mass\left(amu\: or\:\dfrac{g}{mol}\right)}=\mathit n\: formula\: units/molecule}\)
- (AxBy)n = AnxBny
Glosario
- composición porcentual
- Porcentaje en masa de los varios elementos en un compuesto.
- masa de fórmula empírica
- Suma de masas atómicas promedio para todos los átomos representados en una fórmula empírica.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


