6.5: Variaciones periódicas en las propiedades del elemento
- Page ID
- 1849
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Describir y explicar las tendencias observadas en el tamaño atómico, la energía de ionización y la afinidad electrónica de los elementos.
Los elementos en grupos (columnas verticales) de la tabla periódica exhiben un comportamiento químico similar. Esta similitud ocurre porque los miembros de un grupo tienen el mismo número y distribución de electrones en sus capas de valencia. Sin embargo, también hay otros patrones en las propiedades químicas en la tabla periódica. Por ejemplo, a medida que avanzamos hacia abajo en un grupo, aumenta el carácter metálico de los átomos. El oxígeno, en la parte superior del Grupo 16 (6A), es un gas sin color; en la mitad del grupo, el selenio es un sólido semiconductor; y, hacia el fondo, el polonio es un sólido gris plateado que conduce la electricidad.
A medida que atravesamos un período de izquierda a derecha, agregamos un protón al núcleo y un electrón a la capa de valencia con cada elemento sucesivo. A medida que avanzamos en los elementos de un grupo, el número de electrones en la capa de valencia permanece constante, pero el número cuántico principal aumenta por uno cada vez. Una comprensión de la estructura electrónica de los elementos nos permite examinar algunas de las propiedades que rigen su comportamiento químico. Estas propiedades varían periódicamente a medida que cambia la estructura electrónica de los elementos. Son (1) tamaño (radio) de átomos e iones, (2) energías de ionización y (3) afinidades electrónicas.
Variación en el radio covalente
La imagen de la mecánica cuántica hace difícil establecer un tamaño definido de un átomo. Sin embargo, hay varias formas prácticas de definir el radio de los átomos y, por lo tanto, determinar sus tamaños relativos que dan valores aproximadamente similares. Usaremos el radio covalente (Figura \(\PageIndex{1}\)), que se define como la mitad de la distancia entre los núcleos de dos átomos idénticos cuando están unidos por un enlace covalente (esta medida es posible porque los átomos dentro de las moléculas aún conservan gran parte de su identidad atómica).
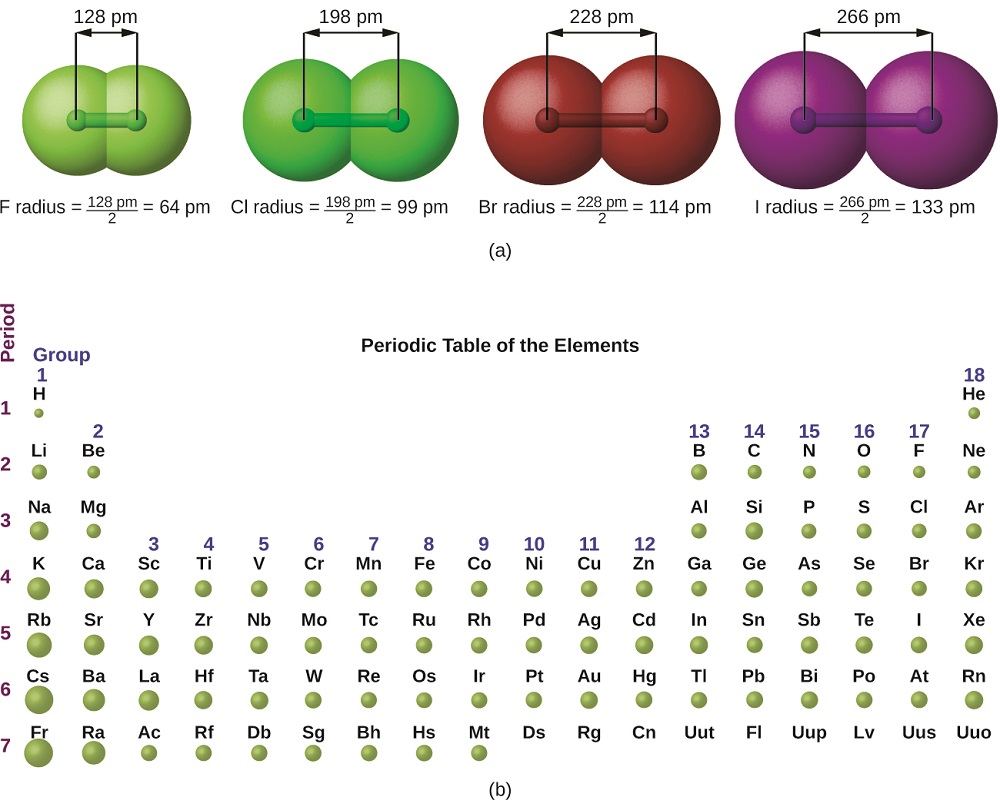
Sabemos que cuando exploramos un grupo en la tabla periódica, el número cuántico principal, n, aumenta por uno para cada elemento. Por lo tanto, los electrones se agregan a una región del espacio que está cada vez más alejada del núcleo. En consecuencia, el tamaño del átomo (y su radio covalente) debe aumentar a medida que aumentamos la distancia de los electrones más externos desde el núcleo. Esta tendencia se ilustra para los radios covalentes de los halógenos en la Tabla \(\PageIndex{1}\) y la Figura \(\PageIndex{1}\). Las tendencias para toda la tabla periódica se pueden ver en la Figura \(\PageIndex{2}\).
| Átomo | Radio covalente (pm) | Carga nuclear |
|---|---|---|
| F | 64 | +9 |
| Cl | 99 | +17 |
| Br | 114 | +35 |
| I | 133 | +53 |
| At | 148 | +85 |
Como se muestra en la Figura \(\PageIndex{2}\), a medida que nos movemos en un período de izquierda a derecha, generalmente encontramos que cada elemento tiene un radio covalente más pequeño que el elemento que lo precede. Esto puede parecer contrario a la intuición porque implica que los átomos con más electrones tienen un radio atómico más pequeño. Esto se puede explicar con el concepto de carga nuclear efectiva, \(Z_{eff}\). Esta es la fuerza ejercida sobre un electrón específico por el núcleo, teniendo en cuenta cualquier repulsión electrón-electron. Para el hidrógeno, solo hay un electrón y, por lo tanto, la carga nuclear (Z) y la carga nuclear efectiva (Zeff) son iguales. Para todos los demás átomos, los electrones internos protegen parcialmente a los electrones externos de la fuerza del núcleo, y por lo tanto:
\[Z_\ce{eff}=Z−shielding\]
El blindaje está determinado por la probabilidad de que otro electrón se encuentre entre el electrón de interés y el núcleo, así como por las repulsiones electrón-electrón que encuentra el electrón de interés. Los electrones del núcleo son adeptos al blindaje, mientras que los electrones en la misma capa de valencia no bloquean la atracción nuclear que experimentan entre sí de manera tan eficiente. Por lo tanto, cada vez que nos movemos de un elemento a otro a lo largo de un período, Z aumenta en uno, pero el blindaje aumenta solo un poco. Por lo tanto, Zeff) aumenta a medida que avanzamos de izquierda a derecha a lo largo de un período. El tirón más fuerte (mayor carga nuclear efectiva) experimentado por los electrones en el lado derecho de la tabla periódica los acerca al núcleo, haciendo que los radios covalentes sean más pequeños.
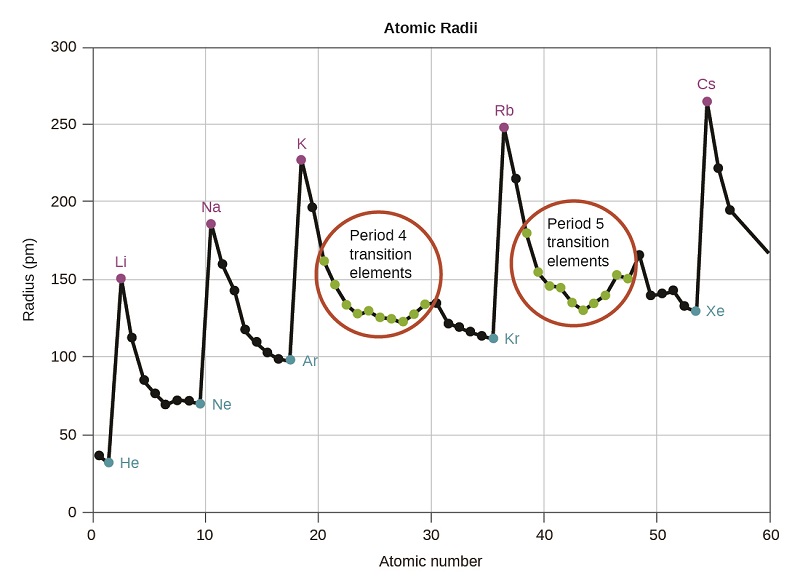
Por lo tanto, como esperaríamos, los electrones más externos o de valencia son los más fáciles de eliminar porque tienen las energías más altas, están más protegidos y están más alejados del núcleo. Como una regla general, cuando los elementos representativos forman cationes, lo hacen por la pérdida de los electrones ns o np que se agregaron por último en el proceso Aufbau. Los elementos de transición, por otro lado, pierden los electrones ns antes de que empiecen a perder los electrones (n - 1)d, aunque los electrones ns se agregan primero, de acuerdo con el principio de Aufbau.
Ejemplo \(\PageIndex{1}\): Clasificación de los radios atómicos
Prediga el orden de aumento del radio covalente para Ge, Fl, Br, Kr.
Solución
El radio aumenta a medida que avanzamos hacia abajo en un grupo, por lo que Ge <Fl (Nota: Fl es el símbolo para flerovium, elemento 114, NO para el flúor). El radio disminuye a medida que nos movemos a través de un período, por lo que Kr <Br <Ge. Juntando las tendencias, obtenemos Kr <Br <Ge <Fl.
Ejercicio \(\PageIndex{1}\)
Dé un ejemplo de un átomo que tiene un tamaño más pequeño que el tamaño del flúor.
- Respuesta
-
Ne or He
Variación en los radios iónicos
El radio iónico es la medida usada para describir el tamaño de un ion. Un catión siempre tiene menos electrones y la misma cantidad de protones que el átomo original; es más pequeño que el átomo del que se deriva (Figura \(\PageIndex{3}\)). Por ejemplo, el radio covalente de un átomo de aluminio (1s22s22p63s23p1) es 118 pm, mientras que el radio iónico de un Al3+ (1s22s22p6) es 68 pm. A medida que se eliminan los electrones de la capa externa de valencia, los electrones restantes que ocupan capas más pequeñas experimentan una mayor carga nuclear efectiva Zeff (como se comentó) y se acercan aún más al núcleo.

Los cationes con cargas más grandes son más pequeños que los cationes con cargas más pequeñas (por ejemplo, V2+ tiene un radio iónico de 79 pm, mientras que el de V3+ es 64 pm). Continuando con los grupos de la tabla periódica, encontramos que los cationes de elementos sucesivos con la misma carga generalmente tienen radios más grandes, correspondientes a un aumento en el número cuántico principal, n.
Un anión (ion negativo) se forma mediante la adición de uno o más electrones a la capa de valencia de un átomo. Esto resulta en una mayor repulsión entre los electrones y una disminución en \(Z_{eff}\) por el electrón. Ambos efectos (el aumento del número de electrones y la disminución de Zeff) hacen que el radio de un anión sea mayor que el del átomo principal (Figura \(\PageIndex{3}\)). Por ejemplo, un átomo de azufre (Ne]3s23p4) tiene un radio covalente de 104 pm, mientras que el radio iónico del anión sulfuro ([Ne]3s23p6) es de 170 pm. Para elementos consecutivos que proceden de cualquier grupo, los aniones tienen números cuánticos principales más grandes y, por lo tanto, radios más grandes.
Se dice que los átomos y los iones que tienen la misma configuración electrónica son isoelectrónicos. Ejemplos de especies isoelectrónicas son N3–, O2–, F–, Ne, Na+, Mg2+, y Al3+ (1s22s22p6) Otra serie isoelectrónica es P3–, S2–, Cl–, Ar, K+, Ca2+, y Sc3+ ([Ne]3s23p6). Para los átomos o iones que son isoelectrónicos, el número de protones determina el tamaño. Cuando la carga nuclear es más grande, el radio en una serie de iones y átomos isoelectrónicos es más pequeño.
Variaciones en las energías de ionización
La cantidad de energía requerida para eliminar el electrón más débilmente unido de un átomo gaseoso en su estado fundamental se llama su primera energía de ionización (IE1). La primera energía de ionización para un elemento, X, es la energía requerida para formar un catión con una carga de +1:
La energía requerida para eliminar el segundo electrón más débilmente unido se llama la segunda energía de ionización (IE2).
La energía requerida para eliminar el tercer electrón es la tercera energía de ionización, y así sucesivamente. Siempre se requiere energía para eliminar los electrones de los átomos o iones, por lo que los procesos de ionización son endotérmicos y los valores de IE siempre son positivos. Para los átomos más grandes, el electrón más débilmente unido se encuentra más alejado del núcleo y, por lo tanto, es más fácil de eliminar. Por lo tanto, a medida que aumenta el tamaño (radio atómico), la energía de ionización debería disminuir. Al relacionar esta lógica con lo que acabamos de aprender sobre los radios, esperaríamos que las energías de ionización primero disminuyan en un grupo y aumenten a lo largo de un período.
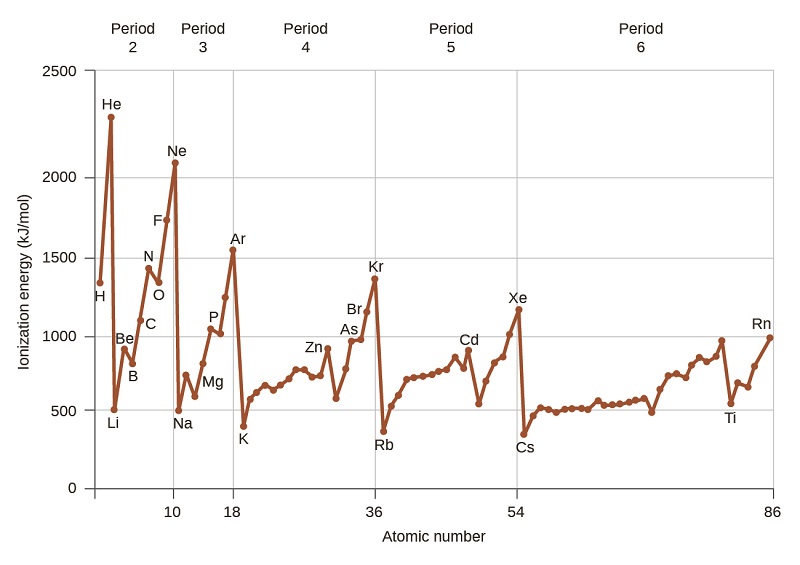
La figura \(\PageIndex{4}\) grafica la relación entre la primera energía de ionización y el número atómico de varios elementos. Dentro de un período, los valores de la primera energía de ionización para los elementos IE1 generalmente aumentan con el aumento de Z. En un grupo, el valor de IE1 generalmente disminuye con el aumento de Z. Sin embargo, existen algunas desviaciones sistemáticas de esta tendencia. Tenga en cuenta que la energía de ionización del boro (número atómico 5) es menor que la del berilio (número atómico 4), aunque la carga nuclear del boro es mayor en un protón. Esto se puede explicar porque la energía de las subcapas aumenta a medida que aumenta l, debido a la penetración y el blindaje (como se explicó anteriormente en este capítulo). Dentro de cualquier capa, los electrones s son más bajos en energía que los electrones p. Esto significa que un electrón s es más difícil de eliminar de un átomo que un electrón p en la misma capa. El electrón eliminado durante la ionización del berilio ([He]2s2) es un electrón s, mientras que el electrón eliminado durante la ionización del boro ([He]2s22p1) es un electrón p; esto da como resultado una primera energía de ionización más baja para el boro, aunque su carga nuclear es mayor en un protón. Por lo tanto, vemos una pequeña desviación de la tendencia predicha que ocurre cada vez que comienza una nueva subcapa.
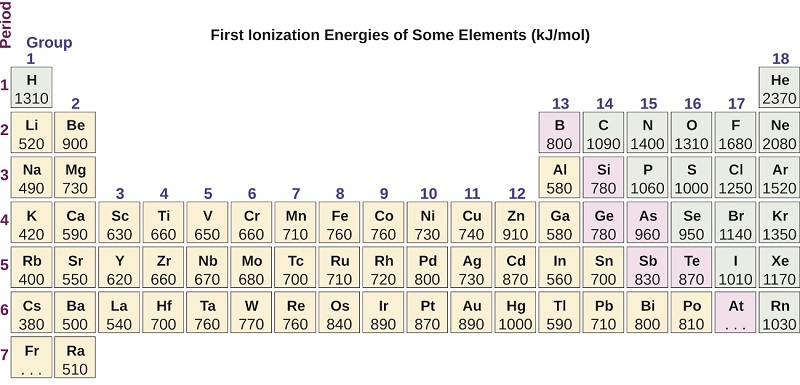
Otra desviación ocurre cuando los orbitales se llenan más de la mitad. La primera energía de ionización para el oxígeno es un poco menos que la del nitrógeno, a pesar de la tendencia a aumentar los valores de IE1 a lo largo de un período. Al observar el diagrama orbital del oxígeno, podemos ver que al eliminar un electrón se eliminará la repulsión electrón-electrón causada por el apareamiento de los electrones en el orbital 2p y se obtendrá un orbital medio lleno (que es energéticamente favorable). Se producen cambios análogos en los períodos sucesivos (tenga en cuenta la caída del azufre después del fósforo en la Figura \(\PageIndex{4}\).

Eliminar un electrón de un catión es más difícil que eliminar un electrón de un átomo neutro debido a la mayor atracción electrostática del catión. Del mismo modo, eliminar un electrón de un catión con una carga positiva más alta es más difícil que eliminar un electrón de un ion con una carga más baja. Así, las energías de ionización sucesivas para un elemento siempre aumentan. Como se ve en la Tabla \(\PageIndex{2}\), hay un gran aumento en las energías de ionización (cambio de color) para cada elemento. Este salto corresponde a la eliminación de los electrones centrales, que son más difíciles de eliminar que los electrones de valencia. Por ejemplo, Sc y Ga tienen tres electrones de valencia, por lo que el rápido aumento de la energía de ionización se produce después de la tercera ionización.
| Elemento | IE1 | IE2 | IE3 | IE4 | IE5 | IE6 | IE7 |
|---|---|---|---|---|---|---|---|
| K | 418.8 | 3051.8 | 4419.6 | 5876.9 | 7975.5 | 9590.6 | 11343 |
| Ca | 589.8 | 1145.4 | 4912.4 | 6490.6 | 8153.0 | 10495.7 | 12272.9 |
| Sc | 633.1 | 1235.0 | 2388.7 | 7090.6 | 8842.9 | 10679.0 | 13315.0 |
| Ga | 578.8 | 1979.4 | 2964.6 | 6180 | 8298.7 | 10873.9 | 13594.8 |
| Ge | 762.2 | 1537.5 | 3302.1 | 4410.6 | 9021.4 | No disponible | No disponible |
| As | 944.5 | 1793.6 | 2735.5 | 4836.8 | 6042.9 | 12311.5 | No disponible |
Ejemplo \(\PageIndex{2}\): Clasificación DE ENERGÍAS DE IONIZACIÓN
Prediga el orden de aumento de energía para los siguientes procesos: IE1 para Al, IE1 para Tl, IE2 para Na, IE3 para Al.
Solución
Eliminar el electrón 6p1 de Tl es más fácil que eliminar el electrón 3p1 de Al porque el orbital n más alto está más alejado del núcleo, por lo que IE1(Tl) <IE1(Al). Ionizando el tercer electrón de
\[\ce{Al}\hspace{20px}\ce{(Al^2+⟶Al^3+ + e- )} \nonumber\]
requiere más energía porque el catión A2+ ejerce un impulso más fuerte sobre el electrón que el átomo de Al neutro, por eso IE1(Al) <IE3(Al). La segunda energía de ionización para el sodio elimina un electrón de núcleo, que es un proceso de energía mucho mayor que la eliminación de los electrones de valencia. Poniendo todo esto junto, obtenemos:
IE1(Tl) < IE1(Al) < IE3(Al) < IE2(Na).
Ejercicio \(\PageIndex{2}\)
¿Que tiene el valor más bajo para IE1: O, Po, Pb, or Ba?
- Respuesta
-
Ba
Variaciones en las afinidades electrónicas
La afinidad de electrones [EA] es el cambio de energía para el proceso de agregar un electrón a un átomo gaseoso para formar un anión (ion negativo).
Este proceso puede ser endotérmico o exotérmico, dependiendo del elemento. El EA de algunos de los elementos se muestra en la Figura \(\PageIndex{6}\). Puedes ver que muchos de estos elementos tienen valores negativos de EA, lo que significa que la energía se libera cuando el átomo gaseoso acepta un electrón. Sin embargo, para algunos elementos, se requiere energía para que el átomo se cargue negativamente y el valor de su EA es positivo. Al igual que con la energía de ionización, los valores de EA posteriores se asocian con la formación de iones con más carga. El segundo EA es la energía asociada con la adición de un electrón a un anión para formar un ion -2, y así sucesivamente.
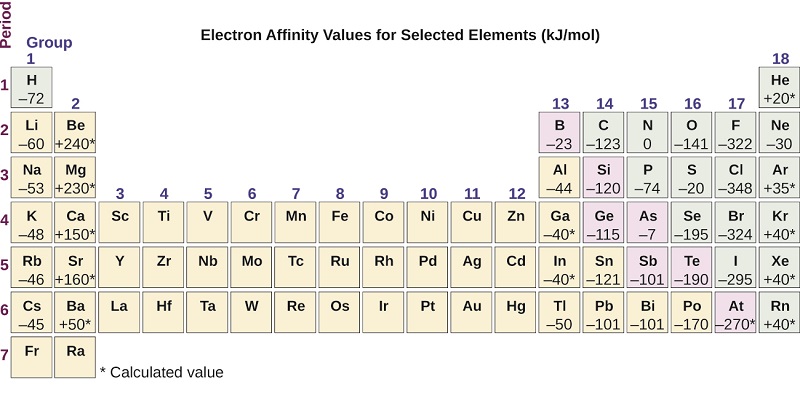
Como podríamos predecir, es más fácil agregar un electrón a través de una serie de átomos a medida que aumenta la carga nuclear efectiva de los átomos. A medida que avanzamos de izquierda a derecha a lo largo de un período, los EA tienden a ser más negativos. Las excepciones encontradas entre los elementos del grupo 2 (2A), el grupo 15 (5A) y el grupo 18 (8A) pueden entenderse en base a la estructura electrónica de estos grupos. Los gases nobles, grupo 18 (8A), tienen una capa completamente llena y el electrón entrante se debe agregar a un nivel n más alto, lo que es más difícil de hacer. El grupo 2 (2A) tiene una subcapa ns rellena, por lo que el siguiente electrón agregado entra en la energía np más alta, por lo que, nuevamente, el valor de EA observado no es como lo predeciría la tendencia. Finalmente, el grupo 15 (5A) tiene una subcapa np medio llena y el siguiente electrón debe emparejarse con un electrón np existente. En todos estos casos, la estabilidad relativa inicial de la configuración electrónica interrumpe la tendencia en EA.
También podemos esperar que el átomo en la parte superior de cada grupo tenga el mayor EA; sus primeros potenciales de ionización sugieren que estos átomos tienen las mayores cargas nucleares efectivas. Sin embargo, a medida que avanzamos hacia abajo en un grupo, vemos que el segundo elemento en el grupo con mayor frecuencia tiene el mayor EA. La reducción de la EA del primer miembro se puede atribuir al pequeño tamaño de la capa n = 2 y las grandes repulsiones electrón-electrón resultantes. Por ejemplo, el cloro, con un valor de EA de –348 kJ / mol, tiene el valor más alto de cualquier elemento en la tabla periódica. La EA de flúor es –322 kJ / mol. Cuando agregamos un electrón a un átomo de flúor para formar un anión fluoruro (F-), agregamos un electrón a la capa n = 2. El electrón es atraído hacia el núcleo, pero también hay una repulsión significativa de los otros electrones ya presentes en esta pequeña capa de valencia. El átomo de cloro tiene la misma configuración electrónica en la capa de valencia, pero debido a que el electrón entrante va a la capa n = 3, ocupa una región del espacio considerablemente mayor y las repulsiones electrón-electrón se reducen. El electrón entrante no experimenta tanta repulsión y el átomo de cloro acepta un electrón adicional más fácilmente.
Las propiedades analizadas en esta sección (el tamaño de los átomos e iones, la carga nuclear efectiva, las energías de ionización y las afinidades electrónicas) son fundamentales para comprender la reactividad química. Por ejemplo, porque el flúor tiene un EA energéticamente favorable y una gran barrera energética para la ionización (IE), es mucho más fácil formar aniones de flúor que los cationes. Las propiedades metálicas, incluyendo la conductividad y la maleabilidad (la capacidad de formar láminas) dependen de tener electrones que se puedan eliminar fácilmente. Por lo tanto, los caracteres metálicos aumentan a medida que avanzamos hacia abajo en un grupo y disminuimos a lo largo de un período en la misma tendencia observada para el tamaño atómico porque es más fácil eliminar un electrón que está más alejado del núcleo.
Resumen
Las configuraciones electrónicas nos permiten entender muchas tendencias periódicas. El radio covalente aumenta a medida que avanzamos hacia abajo en un grupo porque aumenta el nivel n (el tamaño orbital). El radio covalente disminuye principalmente a medida que nos movemos de izquierda a derecha a lo largo de un período debido a que la carga nuclear efectiva experimentada por los electrones aumenta, y los electrones están más apretados hacia el núcleo. Los radios aniónicos son más grandes que el átomo principal, mientras que los radios catiónicos son más pequeños, porque el número de electrones de valencia ha cambiado, mientras que la carga nuclear se ha quedado constante. La energía de ionización (la energía asociada con la formación de un catión) disminuye en un grupo y en su mayoría aumenta a lo largo de un período porque es más fácil eliminar un electrón de un orbital más grande y de mayor energía. La afinidad electrónica (la energía asociada con la formación de un anión) es más favorable (exotérmica) cuando los electrones se colocan en orbitales de menor energía, más cerca del núcleo. Por lo tanto, la afinidad electrónica se vuelve cada vez más negativa a medida que nos movemos de izquierda a derecha a través de la tabla periódica y disminuye a medida que avanzamos hacia abajo en un grupo. Tanto para IE como para datos de afinidad de electrones, hay excepciones a las tendencias cuando se trata de subcapas completamente llenas o medio llenas.
Glosario
- radio covalente
- La mitad de la distancia entre los núcleos de dos átomos idénticos cuando están unidos por un enlace covalente.
- carga nuclear efectiva
- Carga que conduce a la fuerza de Coulomb ejercida por el núcleo sobre un electrón, calculada como la carga nuclear menos el blindaje.
- afinidad electronica
- Energía requerida para agregar un electrón a un átomo gaseoso para formar un anión.
- energía de ionización
- Energía requerida para eliminar un electrón de un átomo o ion gaseoso. El número asociado (por ejemplo, la segunda energía de ionización) corresponde a la carga del ion producido (X2+).
- isoelectrónico
- Grupo de iones o átomos que tienen configuraciones electrónicas idénticas.
Contribuyentes
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


