10.2: Propiedades de los líquidos
- Page ID
- 1878
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Distinguir entre las fuerzas adhesivas y cohesivas.
- Definir la viscosidad, tensión superficial y el aumento capilar.
- Describir los roles de las fuerzas de atracción intermoleculares en cada una de estas propiedades / fenómenos.
Cuando vierte un vaso de agua o llena un automóvil con gasolina observa que el agua y la gasolina fluyen libremente. Pero cuando vierte el jarabe en los panqueques o agrega el aceite al motor de un automóvil, observa que el jarabe y el aceite de motor no fluyen tan fácilmente. La viscosidad de un líquido es una medida de su resistencia al flujo. El agua, la gasolina y otros líquidos que fluyen libremente tienen una baja viscosidad. La miel, el jarabe, el aceite de motor y otros líquidos que no fluyen libremente, como los que se muestran en la Figura \(\PageIndex{1}\), tienen viscosidades más altas. Podemos medir la viscosidad por midiendo la velocidad a la que una bola de metal cae a través de un líquido (la bola cae más lentamente a través de un líquido más viscoso) o midiendo la velocidad a la que un líquido fluye a través de un tubo estrecho (los líquidos más viscosos fluyen más lentamente).

Los FMI entre las moléculas de un líquido, el tamaño y la forma de las moléculas y la temperatura determinan la facilidad con la que fluye un líquido. Como se muestra en la Tabla \(\PageIndex{1}\), cuanto más estructuralmente complejas son las moléculas en un líquido y cuanto más fuertes son los FMI entre ellas, más difícil es que se muevan entre sí y mayor es la viscosidad del líquido. A medida que aumenta la temperatura, las moléculas se mueven más rápidamente y sus energías cinéticas están en mejores condiciones para superar las fuerzas que las mantienen juntas; así, la viscosidad del líquido disminuye.
| Sustancia | Fórmula | Viscosidad (mPa·s) |
|---|---|---|
| agua | H2O | 0.890 |
| mercurio | Hg | 1.526 |
| etanol | C2H5OH | 1.074 |
| octano | C8H18 | 0.508 |
| etilenglicol | CH2(OH)CH2(OH) | 16.1 |
| miel | variable | ~2,000–10,000 |
| aceite de motor | variable | ~50–500 |
Los diversos IMF entre las moléculas idénticas de una sustancia son ejemplos de fuerzas cohesivas. Las moléculas dentro de un líquido están rodeadas por otras moléculas y son atraídas igualmente en todas las direcciones por las fuerzas cohesivas dentro del líquido. Sin embargo, las moléculas en la superficie de un líquido son atraídas solo por aproximadamente la mitad de las moléculas. Debido a las atracciones moleculares desequilibradas en las moléculas de la superficie, los líquidos se contraen para formar una forma que minimiza el número de moléculas en la superficie, es decir, la forma con el área de superficie mínima. Una pequeña gota de líquido tiende a asumir una forma esférica, como se muestra en la Figura \(\PageIndex{2}\), porque en una esfera, la relación entre el área de superficie y el volumen es mínima. Las gotas más grandes se ven más afectadas por la gravedad, la resistencia del aire, las interacciones superficiales, etc., y como resultado, son menos esféricas.
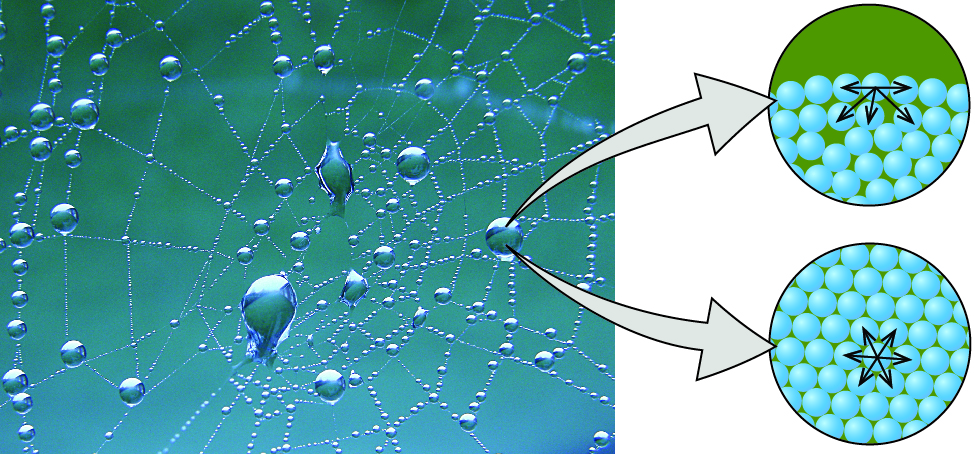
La tensión superficial se define como la energía requerida para aumentar el área superficial de un líquido, o la fuerza requerida para aumentar la longitud de una superficie líquida en una cantidad dada. Esta propiedad resulta de las fuerzas cohesivas entre las moléculas en la superficie de un líquido, y hace que la superficie de un líquido se comporte como una membrana de goma estirada. Las tensiones superficiales de varios líquidos se presentan en la Tabla \(\PageIndex{2}\).
| Sustancia | Fórmula | Tensión superficial (mN/m) |
|---|---|---|
| agua | H2O | 71.99 |
| mercurio | Hg | 458.48 |
| etanol | C2H5OH | 21.97 |
| octano | C8H18 | 21.14 |
| etilenglicol | CH2(OH)CH2(OH) | 47.99 |
Entre los líquidos comunes, el agua exhibe una tensión superficial distintivamente alta debido al fuerte enlace de hidrógeno entre sus moléculas. Como resultado de esta alta tensión superficial, la superficie del agua representa una "piel relativamente dura" que puede soportar una fuerza considerable alta sin romperse. Una aguja de acero cuidadosamente colocada sobre el agua flotará. Algunos insectos, como el que se muestra en la Figura \(\PageIndex{3}\), aunque son más densos que el agua, se mueven sobre su superficie porque están soportados por la tensión superficial.

Los FMI de atracción entre dos moléculas diferentes se llaman las fuerzas adhesivas. Considere lo que sucede cuando el agua entra en contacto con alguna superficie. Si las fuerzas adhesivas entre las moléculas de agua y las moléculas de la superficie son débiles en comparación con las fuerzas cohesivas entre las moléculas de agua, el agua no "moja" la superficie. Por ejemplo, el agua no moja las superficies encerradas o muchos plásticos como el polietileno. El agua forma gotas en estas superficies porque las fuerzas cohesivas dentro de las gotas son mayores que las fuerzas adhesivas entre el agua y el plástico. El agua se extiende sobre el vidrio porque la fuerza adhesiva entre el agua y el vidrio es mayor que las fuerzas cohesivas dentro del agua. Cuando el agua está confinada en un tubo de vidrio, su menisco (superficie) tiene una forma cóncava porque el agua moja el vidrio y se arrastra por el costado del tubo. Por otro lado, las fuerzas cohesivas entre los átomos de mercurio son mucho mayores que las fuerzas adhesivas entre el mercurio y el vidrio. Por esta razón, el mercurio no humedece el vidrio, y forma un menisco convexo cuando está confinado en un tubo porque las fuerzas cohesivas dentro del mercurio tienden a convertirse en una gota (Figura \(\PageIndex{4}\)).

Si coloca un extremo de una toalla de papel en vino derramado, como se muestra en la Figura \(\PageIndex{5}\), la toalla de papel absorbe el líquido. Un proceso similar ocurre en una toalla de tela cuando la usa para secarse después de ducharse. Estos son ejemplos de acción capilar: cuando un líquido fluye dentro de un material poroso debido a la atracción de las moléculas líquidas hacia la superficie del material y hacia otras moléculas líquidas. Las fuerzas adhesivas entre el líquido y el material poroso, combinadas con las fuerzas cohesivas dentro del líquido, pueden ser lo suficientemente fuertes como para mover el líquido hacia arriba contra la gravedad.
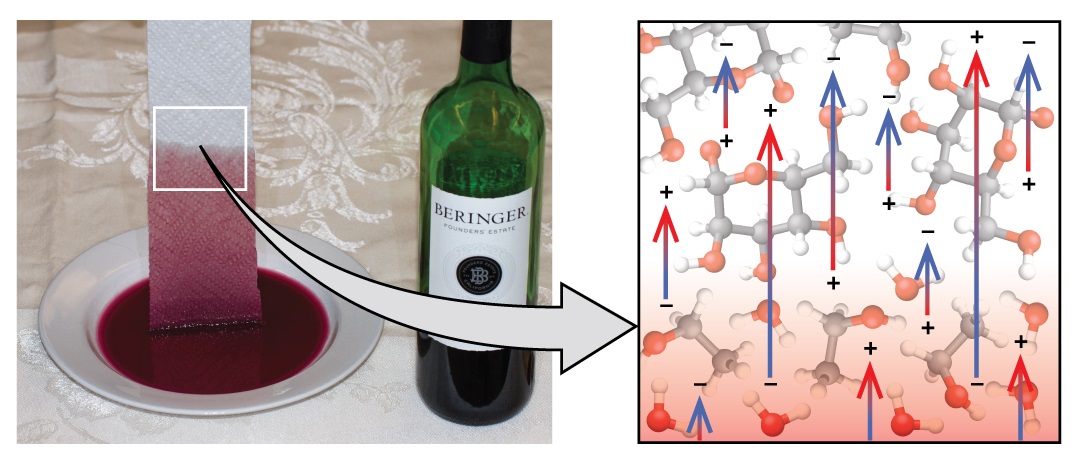
Las toallas absorben líquidos como el agua porque las fibras de una toalla están hechas de moléculas que son atraídas por las moléculas de agua. La mayoría de las toallas de tela están hechas de algodón, y las toallas de papel generalmente están hechas de pulpa de papel. Ambos consisten en moléculas largas de celulosa que contienen muchos grupos -OH. Las moléculas de agua son atraídas por estos grupos -OH y forman enlaces de hidrógeno con ellas, lo que atrae las moléculas de H2O hacia las moléculas de celulosa. Las moléculas de agua también se atraen entre sí, por lo que se extraen grandes cantidades de agua de las fibras de celulosa.
La acción capilar también puede ocurrir cuando un extremo de un tubo de diámetro pequeño se sumerge en un líquido, como se ilustra en la Figura \(\PageIndex{6}\). Si las moléculas líquidas son fuertemente atraídas por las moléculas del tubo, el líquido se arrastra por el interior del tubo hasta que el peso del líquido y las fuerzas adhesivas estén en equilibrio. Cuanto más pequeño es el diámetro del tubo, más alto sube el líquido. Es en parte por la acción capilar que ocurre en las células vegetales llamadas la xilema que el agua y los nutrientes disueltos son llevados desde el suelo a través de las raíces y dentro de una planta. La acción capilar es la base de la cromatografía en capa fina, una técnica de laboratorio que se usa comúnmente para separar pequeñas cantidades de mezclas. Usted depende de un suministro constante de lágrimas para mantener sus ojos lubricados y de la acción capilar para soltar el líquido lagrimal.
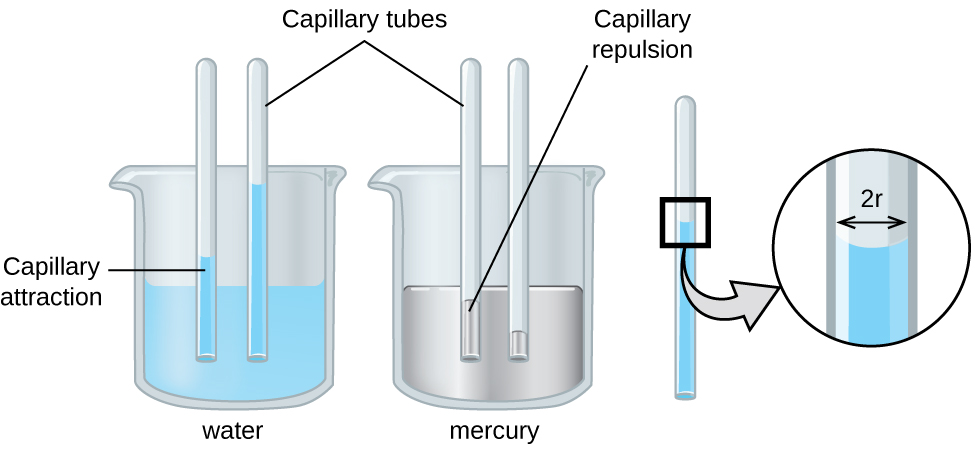
La altura a la que se subirá un líquido en un tubo capilar está determinada por varios factores, como se muestra en la siguiente ecuación:
\[h=\dfrac{2T\cosθ}{rρg} \label{10.2.1}\]
donde- h es la altura del líquido dentro del tubo capilar con respecto a la superficie del líquido fuera del tubo,
- T es la tensión superficial del líquido,
- θ es el ángulo de contacto entre el líquido y el tubo,
- r es el radio del tubo, ρ es la densidad del líquido y
- g es la aceleración debida a la gravedad, 9.8 m/s2.
Ejemplo \(\PageIndex{1}\): aumento capilar
A 25 ° C, ¿Qué tan alto se elevará el agua en un tubo capilar de vidrio con un diámetro interno de 0.25 mm?
Para el agua, T = 71.99 mN/m y ρ = 1.0 g/cm3.
Solución
El líquido se elevará a una altura h dada por la ecuación \(\ref{10.2.1}\) :
\[h=\dfrac{2T\cosθ}{rρg} \nonumber\]
El Newton se define como un kg m/s2, por lo que la tensión superficial proporcionada es equivalente a 0.07199 kg/s2. La densidad proporcionada debe convertirse en unidades que se cancelarán de manera adecuada: ρ = 1000 kg/m3. El diámetro del tubo en metros es de 0.00025 m, por lo que el radio es de 0.000125 m. Para un tubo de vidrio sumergido en agua, el ángulo de contacto es θ = 0°, entonces cos θ = 1. Finalmente, la aceleración debida a la gravedad en la tierra es g = 9.8 m/s2. Sustituyendo estos valores en la ecuación y cancelando unidades, tenemos:
\[h=\mathrm{\dfrac{2(0.07199\:kg/s^2)}{(0.000125\:m)(1000\:kg/m^3)(9.8\:m/s^2)}=0.12\:m=12\: cm}\]
Ejercicio \(\PageIndex{1}\)
El agua sube en un tubo capilar de vidrio a una altura de 8.4 cm. ¿Cuál es el diámetro del tubo capilar?
- Respuesta
-
diámetro = 0.36 mm
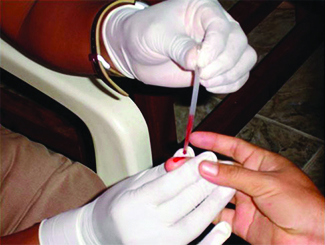
APLICACIONES: LA ACCIÓN CAPILAR SE USA PARA SACAR SANGRE
Muchas pruebas médicas requieren extraer una pequeña cantidad de sangre, por ejemplo, para determinar la cantidad de glucosa en alguien con diabetes o el nivel de hematocrito en un atleta. Este procedimiento se puede realizar fácilmente debido a la acción capilar, la capacidad de un líquido para fluir por un tubo pequeño contra la gravedad, como se muestra en la Figura \(\PageIndex{7}\). Cuando se pincha el dedo, se forma una gota de sangre que se mantiene unida debido a la tensión superficial: las atracciones intermoleculares desequilibradas en la superficie de la gota. Luego, cuando el extremo abierto de un tubo de vidrio de diámetro estrecho toca la gota de sangre, las fuerzas adhesivas entre las moléculas de la sangre y las de la superficie del vidrio extraen la sangre del tubo. La cantidad de sangre que sube por el tubo depende del diámetro del tubo (y del tipo de líquido). Un tubo pequeño tiene un área de superficie relativamente grande para un volumen dado de sangre, lo que resulta en fuerzas de atracción más grandes (relativas), lo que permite que la sangre se extraiga más arriba del tubo. El líquido mismo se mantiene unido por sus propias fuerzas cohesivas. Cuando el peso del líquido en el tubo genera una fuerza hacia abajo igual a la fuerza hacia arriba asociada con la acción capilar, el líquido deja de elevarse.
Conceptos Clave y Resumen
Las fuerzas intermoleculares entre las moléculas en el estado líquido varían según sus identidades químicas y dan como resultado variaciones correspondientes en varias propiedades físicas. Las fuerzas cohesivas entre moléculas similares son responsables de la viscosidad de un líquido (resistencia al flujo) y la tensión superficial (elasticidad de una superficie líquida). Las fuerzas adhesivas entre las moléculas de un líquido y las diferentes moléculas que componen una superficie en contacto con el líquido son responsables de fenómenos como la humectación de la superficie y el aumento de los capilares.
Ecuaciones Clave
- \(h=\dfrac{2T\cosθ}{rρg}\)
Glosario
- Fuerza adhesiva
- fuerza de atracción entre moléculas de diferentes identidades químicas
- acción capilar
- flujo de líquido dentro de un material poroso debido a la atracción de las moléculas líquidas a la superficie del material y a otras moléculas líquidas
- fuerza cohesiva
- fuerza de atracción entre moléculas idénticas
- tensión superficial
- energía requerida para aumentar el área, o longitud, de una superficie líquida en una cantidad dada
- viscosidad
- medida de la resistencia del flujo de un líquido
Contribuyentes
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


