10.3: Transiciones de fase

Última actualización
Guardar como PDF

Page ID: 1879

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

habilidades para desarrollar

Definir las transiciones de fase y las temperaturas de transición de fase.
Explicar la relación entre las temperaturas de transición de fase y las fuerzas de atracción intermoleculares.
Describir los procesos representados por las curvas típicas de calentamiento y enfriamiento, y calcular los flujos de calor y los cambios de entalpía que acompañan a estos procesos.

Somos testigos y usamos los cambios de estado físico, o transiciones de fase, de muchas maneras. Como un ejemplo de importancia global, considere la evaporación, condensación, congelación y fusión del agua. Estos cambios de estado son aspectos esenciales del ciclo del agua de nuestra tierra, así como muchos otros fenómenos naturales y procesos tecnológicos de importancia central para nuestras vidas. En este módulo, se exploran los aspectos esenciales de las transiciones de fase.

La vaporización y la condensación

Cuando un líquido se vaporiza en un recipiente cerrado, las moléculas de gas no pueden escapar. A medida que estas moléculas en fase gaseosa se mueven aleatoriamente, ocasionalmente colisionarán con la superficie de la fase condensada y, en algunos casos, estas colisiones harán que las moléculas vuelvan a entrar en la fase condensada. El cambio de la fase gaseosa al líquido se llama la condensación. Cuando la velocidad de la condensación se vuelve igual a la velocidad de la vaporización, no cambia la cantidad de líquido ni la cantidad de vapor en el recipiente. Se dice que el vapor en el recipiente está en equilibrio con el líquido. Tenga en cuenta que esta no es una situación estática, ya que las moléculas se intercambian continuamente entre las fases condensada y gaseosa. Tal es un ejemplo de equilibrio dinámico, el estado de un sistema en el que los procesos recíprocos (por ejemplo, la vaporización y la condensación) ocurren a velocidades iguales. La presión ejercida por el vapor en equilibrio con un líquido en un recipiente cerrado a una temperatura dada se llama la presión de vapor del líquido (o presión de vapor en equilibrio). El área de la superficie del líquido en contacto con un vapor y el tamaño del recipiente no tienen ningún efecto sobre la presión del vapor, aunque sí afectan el tiempo requerido para alcanzar el equilibrio. Podemos medir la presión de vapor de un líquido cuando colocamos una muestra en un recipiente cerrado, como se ilustra en la Figura \(\PageIndex{1}\), y usamos un manómetro para medir el aumento de presión que se debe al vapor en equilibrio con la fase condensada.

Three images are shown and labeled “a,” “b,” and “c.” Each image shows a round bulb connected on the right to a tube that is horizontal, then is bent vertically, curves, and then is vertical again to make a u-shape. A valve is located in the horizontal portion of the tube. Image a depicts a liquid in the bulb, labeled, “Liquid,” and upward-facing arrows leading away from the surface of the liquid. The phrase, “Molecules escape surface and form vapor” is written below the bulb, and a gray liquid in the u-shaped portion of the tube is shown at equal heights on the right and left sides. Image b depicts a liquid in the bulb, labeled, “Liquid,” and upward-facing arrows leading away from the surface of the liquid to molecules drawn in the upper portion of the bulb. A gray liquid in the u-shaped portion of the tube is shown slightly higher on the right side than on the left side. Image c depicts a liquid in the bulb, labeled, “Liquid,” and upward-facing arrows leading away from the surface of the liquid to molecules drawn in the upper portion of the bulb. There are more molecules present in c than in b. The phrase “Equilibrium reached, vapor pressure determined,” is written below the bulb and a gray liquid in the u-shaped portion of the tube is shown higher on the right side. A horizontal line is drawn level with each of these liquid levels and the distance between the lines is labeled with a double-headed arrow. This section is labeled with the phrase, “Vapor pressure.” — Figura \(\PageIndex{1}\): En un recipiente cerrado, el equilibrio dinámico se alcanza cuando (a) aumenta la velocidad de las moléculas que escapan del líquido para convertirse en gas (b) y, finalmente, (c) es igual a la velocidad de las moléculas de gas que ingresan al líquido. Cuando se alcanza este equilibrio, la presión de vapor del gas es constante, aunque los procesos de vaporización y condensación continúan.

Las identidades químicas de las moléculas en un líquido determinan los tipos (y fuerzas) posibles de atracciones intermoleculares; en consecuencia, diferentes sustancias exhibirán diferentes presiones de vapor de equilibrio. Las fuerzas de atracción intermoleculares relativamente fuertes servirán para impedir la vaporización y favorecerán la "recaptura" de moléculas de fase gaseosa cuando colisionan con la superficie del líquido, lo que da como resultado una presión de vapor relativamente baja. Las atracciones intermoleculares débiles presentan menos barrera para la vaporización y una probabilidad reducida de recaptura de gas, produciendo presiones de vapor relativamente altas. El siguiente ejemplo ilustra esta dependencia de la presión de vapor de las fuerzas de atracción intermoleculares.

Ejemplo \(\PageIndex{1}\): EXPLICANDO LA PRESIÓN DE VAPOR EN TÉRMINOS DE IMFS

Dado las fórmulas estructurales que se muestran para estos cuatro compuestos, explique sus presiones de vapor relativas en términos de tipos y extensiones de FMI:

Solución

El éter dietílico tiene un dipolo muy pequeño y la mayoría de sus atracciones intermoleculares son las fuerzas de Londres. Aunque esta molécula es la más grande de las cuatro consideradas, sus IMF son los más débiles y, como resultado, sus moléculas escapan más fácilmente del líquido. También tiene la presión de vapor más alta. Debido a su tamaño más pequeño, el etanol exhibe fuerzas de dispersión más débiles que el éter dietílico. Sin embargo, el etanol es capaz de unirse con hidrógeno y, por lo tanto, exhibe IMFs más fuertes en general, lo que significa que escapan menos moléculas del líquido a cualquier temperatura dada, por lo que el etanol tiene una presión de vapor más baja que el éter dietílico. El agua es mucho más pequeña que cualquiera de las sustancias anteriores y exhibe fuerzas de dispersión más débiles, pero su extenso enlace de hidrógeno proporciona atracciones intermoleculares más fuertes, menos moléculas que escapan del líquido y una presión de vapor más baja que la del éter dietílico o el etanol. El etilenglicol tiene dos grupos -OH, por lo que, al igual que el agua, exhibe una extensa unión de hidrógeno. Es mucho más grande que el agua y por lo tanto experimenta fuerzas más grandes de Londres. Sus FMI generales son la mayor de estas cuatro sustancias, lo que significa que su tasa de vaporización será la más lenta y, en consecuencia, su presión de vapor será la más baja.

Ejercico \(\PageIndex{1}\)

A 20 ° C, las presiones de vapor de varios alcoholes se dan en esta tabla. Explique estas presiones de vapor en términos de tipos y grados de FMI para estos alcoholes:

Compuesta	metanol CH₃OH	etanol C₂H₅OH	propanol C₃H₇OH	butanol C₄H₉OH
Presión de vapor a 20 °C	11.9 kPa	5.95 kPa	2.67 kPa	0.56 kPa

Respuesta

Todos estos compuestos exhiben enlaces de hidrógeno; estos fuertes IMF son difíciles de superar para las moléculas, por eso, las presiones de vapor son relativamente bajas. A medida que el tamaño de la molécula aumenta de metanol a butanol, aumentan las fuerzas de dispersión, lo que significa que las presiones de vapor disminuyen como se observa:

\[P_{methanol} > P_{ethanol} > P_{propanol} > P_{butanol} \nonumber\]

Cuando aumenta la temperatura, la presión de vapor de un líquido también aumenta debido al aumento de KE promedio de sus moléculas. Recuerde que, a cualquier temperatura dada, las moléculas de una sustancia pasan por un rango de energías cinéticas, con una cierta fracción de moléculas que tienen una energía suficiente para vencer al FMI y escapar del líquido (vaporizarse). A una temperatura más alta, una fracción mayor de moléculas tiene suficiente energía para escapar del líquido, como se muestra en la Figura \(\PageIndex{2}\). El escape de más moléculas por unidad de tiempo y la mayor velocidad promedio de las moléculas que escapan contribuyen a la mayor presión de vapor.

Figura \(\PageIndex{2}\): La temperatura afecta la distribución de las energías cinéticas para las moléculas en un líquido. A la temperatura más alta, más moléculas tienen la energía cinética necesaria, KE, para escapar del líquido a la fase gaseosa.

Puntos de Ebullición

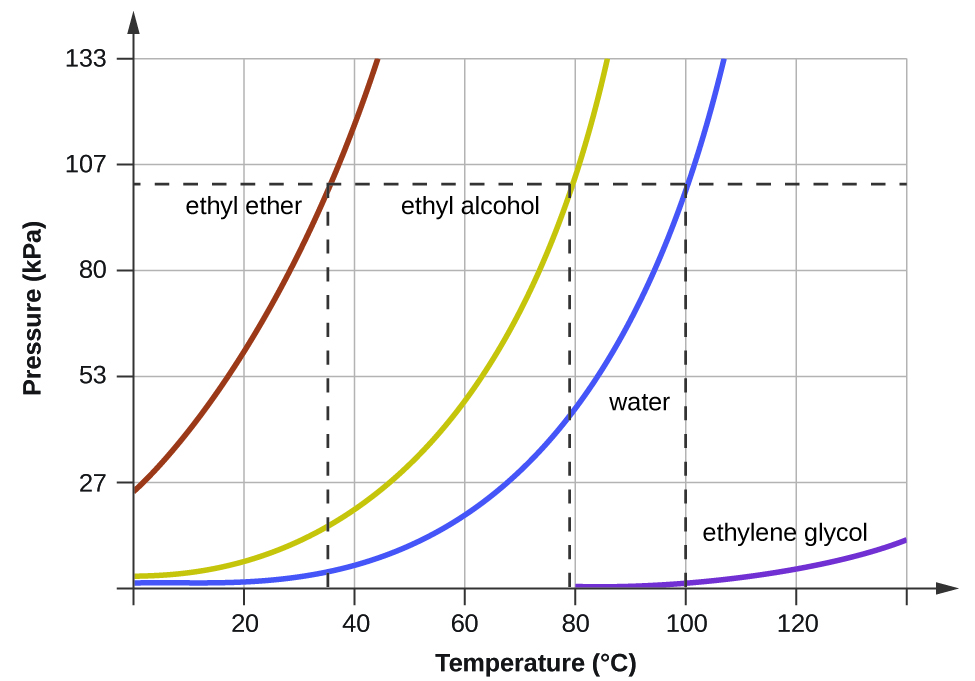
Cuando la presión de vapor aumenta suficiente para ser igual a la presión atmosférica externa, el líquido alcanza su punto de ebullición. El punto de ebullición de un líquido es la temperatura a la cual su presión de vapor de equilibrio es igual a la presión ejercida sobre el líquido por su entorno gaseoso. Para líquidos en recipientes abiertos, esta presión se debe a la atmósfera de la tierra. El punto de ebullición normal de un líquido se define como su punto de ebullición cuando la presión circundante es igual a 1 atm (101.3 kPa). La Figura \(\PageIndex{3}\) muestra la variación en la presión de vapor con la temperatura para varias sustancias diferentes. Teniendo en cuenta la definición de punto de ebullición, se puede ver que estas curvas representan la dependencia del punto de ebullición de un líquido de la presión circundante.

A graph is shown where the x-axis is labeled “Temperature ( degree sign, C )” and has values of 200 to 1000 in increments of 200 and the y-axis is labeled “Pressure ( k P a )” and has values of 20 to 120 in increments of 20. A horizontal dotted line extends across the graph at point 780 on the y-axis while three vertical dotted lines extend from points 35, 78, and 100 to meet the horizontal dotted line. Four lines are graphed. The first line, labeled “ethyl ether,” begins at the point “0 , 200” and extends in a slight curve to point “45, 1000” while the second line, labeled “ethanol”, extends from point “0, 20” to point “88, 1000” in a more extreme curve. The third line, labeled “water,” begins at the point “0, 0” and extends in a curve to point “108, 1000” while the fourth line, labeled “ethylene glycol,” extends from point “80, 0” to point “140, 100” in a very shallow curve. — Figura \(\PageIndex{3}\): Los puntos de ebullición de los líquidos son las temperaturas a las cuales sus presiones de vapor de equilibrio son iguales a la presión de la atmósfera circundante. Los puntos de ebullición normales son los correspondientes a una presión de 1 atm (101.3 kPa.)

Ejemplo \(\PageIndex{2}\): Punto de ebullición a presión reducida

Una presión atmosférica típica en Leadville, Colorado (elevación 10,200 pies) es 68 kPa. Use el gráfico de la Figura \(\PageIndex{3}\) para determinar el punto de ebullición del agua a esta elevación.

Solución

El gráfico de la presión de vapor del agua versus la temperatura en la Figura \(\PageIndex{3}\) indica que la presión de vapor del agua es de 68 kPa a aproximadamente 90 °C. Por lo tanto, a aproximadamente 90 °C, la presión de vapor del agua será igual a la presión atmosférica en Leadville, y el agua hervirá.

Ejercicio \(\PageIndex{2}\)

El punto de ebullición del éter etílico se midió a ser 10 °C en un campamento base en las laderas del Monte Everest. Use la Figura \(\PageIndex{3}\) para determinar la presión atmosférica aproximada en el campamento.

Respuesta: Aproximadamente 40 kPa (0.4 atm)

La ecuación de Clausius-Clapeyron describe la relación cuantitativa entre la presión de vapor de una sustancia y su temperatura:

\[P=Ae^{−ΔH_{vap}/RT} \label{10.4.1}\]

donde

\(ΔH_{vap}\) es la entalpía de vaporización del líquido,
\(R\) es el constante de gas, y
\(\ln A\) es una constante cuyo valor depende de la identidad química de la sustancia.

La ecuación \(\ref{10.4.1}\) a veces se reorganiza en forma logarítmica para producir la ecuación lineal:

\[\ln P=−\dfrac{ΔH_\ce{vap}}{RT}+\ln A \label{10.4.2}\]

Esta ecuación lineal se puede expresar en un formato de dos puntos que sea conveniente para su uso en varios cálculos, como se demuestra en los ejemplos y ejercicios que siguen. Si a temperatura \(T_1\), la presión de vapor es \(P_1\), y a temperatura \(T_2\), la presión de vapor es \(T_2\), las ecuaciones lineales correspondientes son:

\[\ln P_1=−\dfrac{ΔH_\ce{vap}}{RT_1}+\ln A\hspace{20px}\ce{and}\hspace{20px}\ln P_2=−\dfrac{ΔH_\ce{vap}}{RT_2}+\ln A \label{10.4.3}\]

Dado que el constante, ln A, es la misma, estas dos ecuaciones se pueden reorganizar para aislar ln A y luego establecerlas iguales entre sí:

\(\ln P_1+\dfrac{ΔH_\ce{vap}}{RT_1}=\ln P_2+\dfrac{ΔH_\ce{vap}}{RT_2}\label{10.4.5}\)

que se puede combinar en:

\[\ln \left(\dfrac{P_2}{P_1}\right)=\dfrac{ΔH_\ce{vap}}{R} \left( \dfrac{1}{T_1}−\dfrac{1}{T_2}\right) \label{10.4.6}\]

Ejemplo \(\PageIndex{3}\): Estimación de la entalpía de la vaporización

El isooctano (2,2,4-trimetilpentano) tiene una clasificación de octano de 100. Se usa como uno de los estándares para el sistema de clasificación del octano para la gasolina. A 34.0 °C, la presión de vapor del isooctano es 10.0 kPa, y a 98.8 °C, su presión de vapor es 100.0 kPa. Use esta información para estimar la entalpía de vaporización para el isooctano.

Solución

La entalpía de vaporización, \(ΔH_\ce{vap}\), se puede determinar usando la ecuación de Clausius-Clapeyron (Ecuación \(\ref{10.4.1}\)):

\[ln\left(\dfrac{P_2}{P_1}\right)=\dfrac{ΔH_\ce{vap}}{R}\left(\dfrac{1}{T_1}−\dfrac{1}{T_2}\right) \nonumber\]

Como tenemos dos valores de presión-temperatura de vapor (T₁ = 34.0 °C = 307.2 K, P₁ = 10.0 kPa y T₂ = 98.8 °C = 372.0 K, P₂= 100 kPa), podemos sustituirlos en esta ecuación y resolver ΔH_vap. Reorganizando la ecuación de Clausius-Clapeyron y resolviendo los rendimientos de ΔH_vap:

\[ ΔH_\ce{vap} = \dfrac{R⋅\ln\left(\dfrac{P_2}{P_1}\right)}{\left(\dfrac{1}{T_1}−\dfrac{1}{T_2}\right)} = \mathrm{\dfrac{(8.3145\:J/mol⋅K)⋅\ln\left(\dfrac{100\: kPa}{10.0\: kPa}\right)}{\left(\dfrac{1}{307.2\:K}−\dfrac{1}{372.0\:K}\right)} =33,800\: J/mol=33.8\: kJ/mol} \]

Tenga en cuenta que la presión puede estar en cualquier unidad, siempre que estén de acuerdo con ambos valores de P, pero la temperatura debe estar en kelvin para que la ecuación de Clausius-Clapeyron sea válida.

Ejercicio \(\PageIndex{3}\)

A 20.0 °C, la presión de vapor del etanol es 5.95 kPa, y a 63.5 °C, su presión de vapor es 53.3 kPa. Use esta información para estimar la entalpía de vaporización para el etanol.

Respuesta: 47,782 J/mol = 47.8 kJ/mol

Ejemplo \(\PageIndex{4}\):ESTIMACIÓN DE TEMPERATURA (O PRESIÓN DE VAPOR)

Para el benceno (C₆H₆), el punto de ebullición normal es 80.1 °C y la entalpía de vaporización es 30.8 kJ/mol. ¿Cuál es el punto de ebullición del benceno en Denver, donde la presión atmosférica = 83.4 kPa?

Solución

Si la temperatura y la presión de vapor se saben en un punto, junto con la entalpía de vaporización, ΔH_vap, entonces la temperatura que corresponde a una presión de vapor diferente (o la presión de vapor que corresponde a una temperatura diferente) se puede determinar usando el Clausius-Ecuación de Clapeyron (Ecuación \(\ref{10.4.1}\)):

\[\ln\left(\dfrac{P_2}{P_1}\right)=\dfrac{ΔH_\ce{vap}}{R}\left(\dfrac{1}{T_1}−\dfrac{1}{T_2}\right) \nonumber\]

Dado que el punto de ebullición normal es la temperatura a la cual la presión de vapor es igual a la presión atmosférica a nivel del mar, sabemos un valor de temperatura de presión de vapor (T₁= 80.1 °C = 353.3 K, P₁= 101.3 kPa, ΔH_vap= 30.8 kJ / mol) y desea encontrar la temperatura (T₂) que corresponde a la presión de vapor P₂= 83.4 kPa. Podemos sustituir estos valores en la ecuación de Clausius-Clapeyron y luego resolver T₂. Reorganizando la ecuación de Clausius-Clapeyron y resolviendo los rendimientos de T₂:

\[\begin{align*}
T_2&=\left(\dfrac{−R⋅\ln\left(\dfrac{P_2}{P_1}\right)}{ΔH_\ce{vap}}+\dfrac{1}{T_1}\right)^{−1}=\mathrm{\left(\dfrac{−(8.3145\:J/mol⋅K)⋅\ln\left(\dfrac{83.4\:kPa}{101.3\:kPa}\right)}{30,800\: J/mol}+\dfrac{1}{353.3\:K}\right)^{−1}}\\
&=\mathrm{346.9\: K\: or\:73.8^\circ C}
\end{align*}\]

Ejercicio \(\PageIndex{4}\)

Para la acetona \(\ce{(CH3)2CO}\), el punto de ebullición normal es 56.5 °C y la entalpía de vaporización es 31.3 kJ/mol. ¿Cuál es la presión de vapor de la acetona a 25.0 °C?

Respuesta: 30.1 kPa

Entalpía de vaporización

La vaporización es un proceso endotérmico. El efecto del enfriamiento puede ser evidente cuando sales de una piscina o una ducha. Cuando el agua de tu piel se evapora, elimina el calor de tu piel y te hace sentir frío. El cambio de energía asociado con el proceso de vaporización es la entalpía de vaporización, ΔH_vap. Por ejemplo, la vaporización de agua a temperatura estándar está representada por:

\[\ce{H2O}(l)⟶\ce{H2O}(g)\hspace{20px}ΔH_\ce{vap}=\mathrm{44.01\: kJ/mol}\]

Como se describe en el capítulo sobre la termoquímica, lo contrario de un proceso endotérmico es un proceso exotérmico. Y así, la condensación de un gas libera calor:

\[\ce{H2O}(g)⟶\ce{H2O}(l)\hspace{20px}ΔH_\ce{con}=−ΔH_\ce{vap}=\mathrm{−44.01\:kJ/mol}\]

Ejemplo \(\PageIndex{5}\): Usando LA ENTALPÍA DE la VAPORIZACIÓN

Una forma en que nuestro cuerpo se enfría es mediante la evaporación del agua en el sudor (Figura \(\PageIndex{4}\)). En climas muy calurosos, podemos perder hasta 1.5 L de sudor por día. Aunque el sudor no es agua pura, podemos obtener un valor aproximado de la cantidad de calor eliminada por evaporación suponiendo que lo sea. ¿Cuánto calor se requiere para evaporar 1.5 L de agua (1.5 kg) a T = 37 °C (temperatura corporal normal); ΔH_vap = 43.46 kJ / mol a 37 °C.

A person’s shoulder and neck are shown and their skin is covered in beads of liquid. — Figura \(\PageIndex{4}\): La evaporación del sudor ayuda a enfriar el cuerpo. (crédito: "Kullez" / Flickr)

Solución

Comenzamos con el volumen conocido de sudor (aproximado como solo agua) y usamos la información dada para convertir a la cantidad de calor necesaria:

\[\mathrm{1.5\cancel{L}×\dfrac{1000\cancel{g}}{1\cancel{L}}×\dfrac{1\cancel{mol}}{18\cancel{g}}×\dfrac{43.46\:kJ}{1\cancel{mol}}=3.6×10^3\:kJ}\]

Así, 3600 kJ de calor se eliminan por la evaporación de 1.5 L de agua.

Ejercicio \(\PageIndex{5}\)

¿Cuánto calor se requiere para evaporar 100.0 g de amoníaco líquido, NH₃, en su punto de ebullición si su entalpía de vaporización es 4.8 kJ / mol?

Respuesta: 28 kJ

Derritiendo y Congelando

Cuando calentamos un sólido cristalino, aumentamos la energía promedio de sus átomos, moléculas o iones y el sólido se calienta. En algún momento, la energía añadida se vuelve lo suficientemente grande como para superar parcialmente las fuerzas que mantienen las moléculas o iones del sólido en sus posiciones fijas, y el sólido comienza el proceso de transición al estado líquido, o al derretimiento. En este punto, la temperatura del sólido deja de aumentar, a pesar de la entrada continua de calor, y permanece constante hasta que todo el sólido se derrita. Solo después de que todo el sólido se haya derretido, el calentamiento continuo aumentará la temperatura del líquido (Figura \(\PageIndex{5}\).

Figura \(\PageIndex{5}\): (a) Este vaso de hielo tiene una temperatura de -12.0 °C. (b) Después de 10 minutos, el hielo ha absorbido suficiente calor del aire para calentarse a 0 °C. Una pequeña cantidad se ha derretido. (c) Treinta minutos después, el hielo ha absorbido más calor, pero su temperatura aún es de 0 °C. El hielo se derrite sin cambiar su temperatura. (d) Solo después de que todo el hielo se haya derretido, el calor absorbido hace que la temperatura aumente a 22.2 °C. (crédito: modificación del trabajo de Mark Ott).

Si dejamos de calentar durante la fusión y colocamos la mezcla de sólido y líquido en un recipiente perfectamente aislado para que no pueda entrar o salir el calor, las fases sólida y líquida permanecen en equilibrio. Esta casi es la situación con una mezcla de hielo y agua en una muy buena botella de termo; casi no entra ni sale calor, y la mezcla de hielo sólido y agua líquida permanece durante horas. En una mezcla de sólido y líquido en equilibrio, los procesos recíprocos de fusión y congelación ocurren a velocidades iguales, y las cantidades de sólido y líquido, por lo tanto, permanecen constantes. La temperatura a la cual las fases sólida y líquida de una sustancia dada están en equilibrio se llama el punto de fusión del sólido o el punto de congelación del líquido. El uso de un término u otro normalmente está dictado por la dirección de la transición de fase que se considera, por ejemplo, de sólido a líquido (fusión) o de líquido a sólido (congelación).

La entalpía de fusión y el punto de fusión de un sólido cristalino dependen de la fuerza de las fuerzas de atracción entre las unidades presentes en el cristal. Las moléculas con fuerzas atractivas débiles forman cristales con puntos de fusión bajos. Los cristales que consisten en partículas con fuerzas atractivas más fuertes se funden a temperaturas más altas.

La cantidad de calor requerido para cambiar un mol de una sustancia del estado sólido al estado líquido es la entalpía de fusión, ΔH_fusde la sustancia. La entalpía de fusión del hielo es 6.0 kJ / mol a 0 °C. La fusión (fusión) es un proceso endotérmico:

\[\ce{H2O}_{(s)} \rightarrow \ce{H2O}_{(l)} \;\; ΔH_\ce{fus}=\mathrm{6.01\; kJ/mol} \label{10.4.9}\]

El proceso recíproco, la congelación, es un proceso exotérmico que tiene un cambio de entalpía de −6.0 kJ/mol a 0 °C:

\[\ce{H_2O}_{(l)} \rightarrow \ce{H_2O}_{(s)}\;\; ΔH_\ce{frz}=−ΔH_\ce{fus}=−6.01\;\mathrm{kJ/mol} \label{10.4.10}\]

La sublimación y la deposición

Algunos sólidos pueden pasar directamente al estado gaseoso, sin pasar por el estado líquido, a través de un proceso conocido como la sublimación. A temperatura ambiente y presión estándar, se sublima un trozo de hielo seco (CO₂ sólido) que parece desaparecer gradualmente sin formar ningún líquido. La nieve y el hielo sublimen a temperaturas por debajo del punto de fusión del agua, un proceso lento que puede ser acelerado por los vientos y las presiones atmosféricas reducidas a grandes altitudes. Cuando se calienta el yodo sólido, el sólido sublime y se convierte en un vapor púrpura intenso (Figura \(\PageIndex{6}\)). El reverso de la sublimación se llama la deposición, un proceso en el cual las sustancias gaseosas se condensan directamente en el estado sólido, evitando el estado líquido. La formación de escarcha es un ejemplo de la deposición.

This figure shows a test tube. In the bottom is a dark substance which breaks up into a purple gas at the top. — Figura \(\PageIndex{6}\): La sublimación del yodo sólido en el fondo del tubo produce un gas púrpura que más tarde se deposita como el yodo sólido en la parte más fría del tubo de arriba. (crédito: modificación del trabajo de Mark Ott)

Al igual que la vaporización, el proceso de la sublimación requiere un aporte de energía para superar las atracciones intermoleculares. La entalpía de la sublimación, ΔHsub, es la energía requerida para convertir un mol de una sustancia del estado sólido al gaseoso. Por ejemplo, la sublimación de dióxido de carbono está representada por:

\[\ce{CO2}(s)⟶\ce{CO2}(g)\hspace{20px}ΔH_\ce{sub}=\mathrm{26.1\: kJ/mol}\]

Del mismo modo, el cambio de la entalpía para el proceso inverso de la deposición es igual en magnitud pero opuesto en signo al del sublimación:

\[\ce{CO2}(g)⟶\ce{CO2}(s)\hspace{20px}ΔH_\ce{dep}=−ΔH_\ce{sub}=\mathrm{−26.1\:kJ/mol}\]

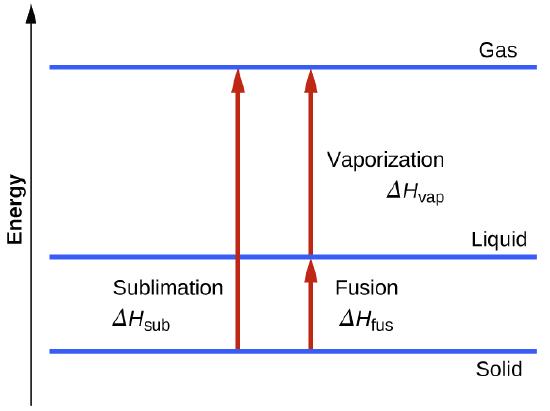
Considere hasta qué punto se deben superar las atracciones intermoleculares para lograr una transición de fase dada. La conversión de un sólido en un líquido requiere que estas atracciones se superen solo parcialmente; la transición al estado gaseoso requiere que se superen por completo. Como resultado, la entalpía de fusión de una sustancia es menor que la entalpía de vaporización. Esta misma lógica se puede usar para derivar una relación aproximada entre las entalpías de todos los cambios de fase para una sustancia dada. Aunque no es una descripción completamente precisa, la sublimación se puede modelar convenientemente como un proceso secuencial de la fusión de dos pasos seguido de vaporización para aplicar la Ley de Hess.

\[\mathrm{solid⟶liquid}\hspace{20px}ΔH_\ce{fus}\\\underline{\mathrm{liquid⟶gas}\hspace{20px}ΔH_\ce{vap}}\\\mathrm{solid⟶gas}\hspace{20px}ΔH_\ce{sub}=ΔH_\ce{fus}+ΔH_\ce{vap}\]

Visto de esta manera, la entalpía de la sublimación de una sustancia se puede estimar como la suma de sus entalpías de fusión y vaporización, como se ilustra en la Figura \(\PageIndex{7}\). Por ejemplo:

A diagram is shown with a vertical line drawn on the left side and labeled “Energy” and three horizontal lines drawn near the bottom, lower third and top of the diagram. These three lines are labeled, from bottom to top, “Solid,” “Liquid” and “Gas.” Near the middle of the diagram, a vertical, upward-facing arrow is drawn from the solid line to the gas line and labeled “Sublimation, delta sign, H, subscript sub.” To the right of this arrow is a second vertical, upward-facing arrow that is drawn from the solid line to the liquid line and labeled “Fusion, delta sign, H, subscript fus.” Above the second arrow is a third arrow drawn from the liquid line to the gas line and labeled, “Vaporization, delta sign, H, subscript vap.” — Figura \(\PageIndex{7}\): Para una sustancia dada, la suma de su entalpía de fusión y la entalpía de vaporización es aproximadamente igual a su entalpía de sublimación.

Curvas de calentamiento y enfriamiento

En el capítulo sobre la termoquímica, se introdujo la relación entre la cantidad de calor absorbido o relacionado por una sustancia, q, y el cambio de temperatura que lo acompaña, ΔT:

\[q=mcΔT\]

donde m es la masa de la sustancia y c es su calor específico. La relación se aplica a la materia que se calienta o enfría, pero que no experimenta un cambio de estado. Cuando una sustancia que se calienta o enfría alcanza una temperatura correspondiente a una de sus transiciones de fase, una mayor ganancia o pérdida de calor es el resultado de disminuir o aumentar las atracciones intermoleculares, en lugar de aumentar o disminuir las energías cinéticas moleculares. Mientras una sustancia está experimentando un cambio de estado, su temperatura permanece constante. La figura \(\PageIndex{8}\) muestra una curva de calentamiento típica.

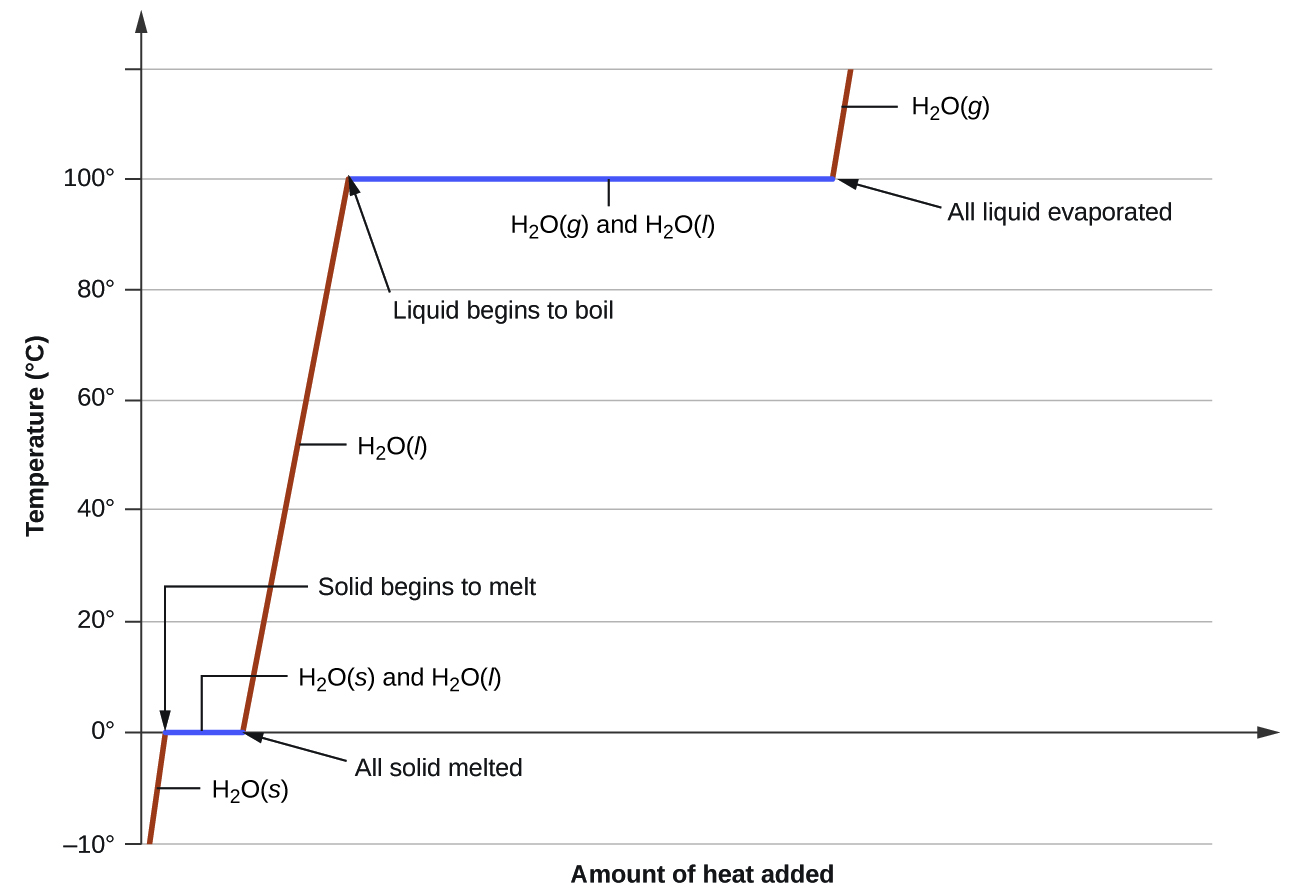
A graph is shown where the x-axis is labeled “Amount of heat added” and the y-axis is labeled “Temperature ( degree sign C )” and has values of negative 10 to 100 in increments of 20. A right-facing horizontal arrow extends from point “0, 0” to the right side of the graph. A line graph begins at the lower left of the graph and moves to point “0” on the y-axis. This segment of the line is labeled “H, subscript 2, O ( s ).” The line then flattens and travels horizontally for a small distance. This segment is labeled “Solid begins to melt” on its left side and “All solid melted” on its right side. The line then goes steeply upward in a linear fashion until it hits point “100” on the y-axis. This segment of the line is labeled “H, subscript 2, O,( l ).” The line then flattens and travels horizontally for a moderate distance. This segment is labeled “Liquid begins to boil” on its left side and “All liquid evaporated” on its right side. The line then rises to a point above “100” on the y-axis. This segment of the line is labeled “H, subscript 2, O ( g ).” — Figura \(\PageIndex{8}\): Una curva de calentamiento típica para una sustancia representa los cambios de temperatura que resultan cuando la sustancia absorbe cantidades crecientes de calor. Las mesetas en la curva (regiones de temperatura constante) se exhiben cuando la sustancia experimenta transiciones de fase.

Considere el ejemplo de calentar una olla de agua a ebullición. Un quemador de estufa suministrará calor a una velocidad aproximadamente constante; inicialmente, este calor sirve para aumentar la temperatura del agua. Cuando el agua alcanza su punto de ebullición, la temperatura permanece constante a pesar de la entrada continua de calor del quemador de la estufa. El agua mantiene esta misma temperatura mientras que esta hirviendo. Si se aumenta el ajuste del quemador para proporcionar calor a un ritmo mayor, la temperatura del agua no aumenta, sino que la ebullición se vuelve más vigorosa (rápida). Este comportamiento también se observa para otras transiciones de fase: por ejemplo, la temperatura permanece constante mientras el cambio de estado está en progreso.

Ejemplo \(\PageIndex{6}\): TOTAL CALOR NECESARIO PARA CAMBIAR LA TEMPERATURA Y LA FASE PARA UNA SUSTANCIA

¿Cuánto calor se requiere para convertir 135 g de hielo a -15 °C en vapor de agua a 120 °C?

Solución

La transición descrita implica los siguientes pasos:

Caliente el hielo de −15 °C a 0 °C
Hielo derretido
Calentar agua de 0 °C a 100 °C
Agua hervida
Calienta el vapor de 100 °C a 120 °C

El calor necesario para cambiar la temperatura de una sustancia determinada (sin cambios en la fase) es: q = m × c × ΔT (consulte el capítulo anterior sobre la termoquímica). El calor necesario para inducir un cambio de fase dado viene dado por q = n × ΔH.

Usando estas ecuaciones con los valores apropiados para el calor específico del hielo, el agua y el vapor, y las entalpías de fusión y vaporización, tenemos:

\[\begin{align*}
q_\ce{total}&=(m⋅c⋅ΔT)_\ce{ice}+n⋅ΔH_\ce{fus}+(m⋅c⋅ΔT)_\ce{water}+n⋅ΔH_\ce{vap}+(m⋅c⋅ΔT)_\ce{steam}\\[7pt]
&=\mathrm{(135\: g⋅2.09\: J/g⋅°C⋅15°C)+\left(135⋅\dfrac{1\: mol}{18.02\:g}⋅6.01\: kJ/mol
\right)}\\[7pt]
&\mathrm{+(135\: g⋅4.18\: J/g⋅°C⋅100°C)+\left(135\: g⋅\dfrac{1\: mol}{18.02\:g}⋅40.67\: kJ/mol\right)}\\[7pt]
&\mathrm{+(135\: g⋅1.84\: J/g⋅°C⋅20°C)}\\[7pt]
&=\mathrm{4230\: J+45.0\: kJ+56,500\: J+305\: kJ+4970\: J}
\end{align*}\]

La conversión de las cantidades en J a kJ permite sumarlas, produciendo el calor total requerido:

\[\mathrm{=4.23\:kJ+45.0\: kJ+56.5\: kJ+305\: kJ+4.97\: kJ=416\: kJ} \nonumber\]

Ejercicio \(\PageIndex{6}\)

¿Cuál es la cantidad total de calor liberado cuando 94.0 g de agua a 80.0 °C se enfría para formar hielo a -30.0 °C?

Respuesta: 40.5 kJ

Resumen

Las transiciones de fase son procesos que convierten la materia de un estado físico a otro estado. Hay seis transiciones de fase entre las tres fases de la materia. La fusión, la vaporización y la sublimación son procesos endotérmicos que requieren un input de calor para superar las atracciones intermoleculares. Las transiciones recíprocas de la congelación, la condensación y la deposición son todos procesos exotérmicos, que involucran calor a medida que se establecen o fortalecen las fuerzas de atracción intermoleculares. Las temperaturas a las cuales ocurren las transiciones de fase están determinadas por las fuerzas relativas de las atracciones intermoleculares y, por lo tanto, dependen de la identidad química de la sustancia.

Ecuaciones Clave

\(P=Ae^{−ΔH_\ce{vap}/RT}\)
\(\ln P=−\dfrac{ΔH_\ce{vap}}{RT}+\ln A\)
\(\ln\left(\dfrac{P_2}{P_1}\right)=\dfrac{ΔH_\ce{vap}}{R}\left(\dfrac{1}{T_1}−\dfrac{1}{T_2}\right)\)

Glosario

punto de ebullición: temperatura a la cual la presión de vapor de un líquido es igual a la presión del gas por encima de él

Ecuación de Clausius-Clapeyron: relación matemática entre la temperatura, la presión de vapor y la entalpía de vaporización de una sustancia

condensación: cambiar de un estado gaseoso a un estado líquido

deposición: cambiar de un estado gaseoso directamente a un estado sólido

equilibrio dinámico: estado de un sistema en el que se producen procesos recíprocos a tasas iguales

congelación: cambiar de estado líquido a estado sólido

punto de congelación: temperatura a la cual las fases sólida y líquida de una sustancia están en equilibrio; ver también punto de fusión

derritiendo: cambiar de un estado sólido a un estado líquido

punto de fusion: temperatura a la cual las fases sólida y líquida de una sustancia están en equilibrio; ver también punto de congelación

punto de ebullición normal: temperatura a la cual la presión de vapor de un líquido es igual a 1 atm (760 torr)

sublimación: cambiar de estado sólido directamente a estado gaseoso

presión de vapor: (también, presión de vapor de equilibrio) presión ejercida por un vapor en equilibrio con un sólido o un líquido a una temperatura dada

vaporización: cambiar del estado líquido al estado gaseoso

Contribuyentes

Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.

Search

Text Color

Text Size

Margin Size

Font Type