1.3: Instrumentos para Análisis

Un ejemplo temprano de un análisis colorimétrico es el método de Nessler para el amoníaco, que se introdujo en 1856. Nessler encontró que agregar una solución alcalina de HgI ₂ y KI a una solución diluida de amoníaco produjo un coloide amarillo a marrón rojizo en el que el color del coloide dependía de la concentración de amoníaco. Además de la muestra, Nessler preparó una serie de soluciones estándar, cada una conteniendo una cantidad conocida de amoníaco, y las colocó en un tubo de vidrio con fondo plano. Al permitir que la luz solar pasara a través de los tubos de abajo hacia arriba, Nessler los observó desde arriba, como se ve en la Figura\(\PageIndex{1}\). Al comparar visualmente el color de la muestra con los colores de los estándares, Nessler pudo estimar la concentración de amoníaco en la muestra.

Figura\(\PageIndex{1}\). El método original de Nessler para comparar el color de dos soluciones. La luz solar natural pasa hacia arriba a través de las muestras y los estándares y el analista ve las soluciones mirando hacia abajo hacia la fuente de luz. La vista superior, que se muestra a la derecha, es lo que ve el analista. Para estimar la concentración del analito, el analista intercambia estándares hasta que el color de la muestra caiga entre el color de dos patrones.

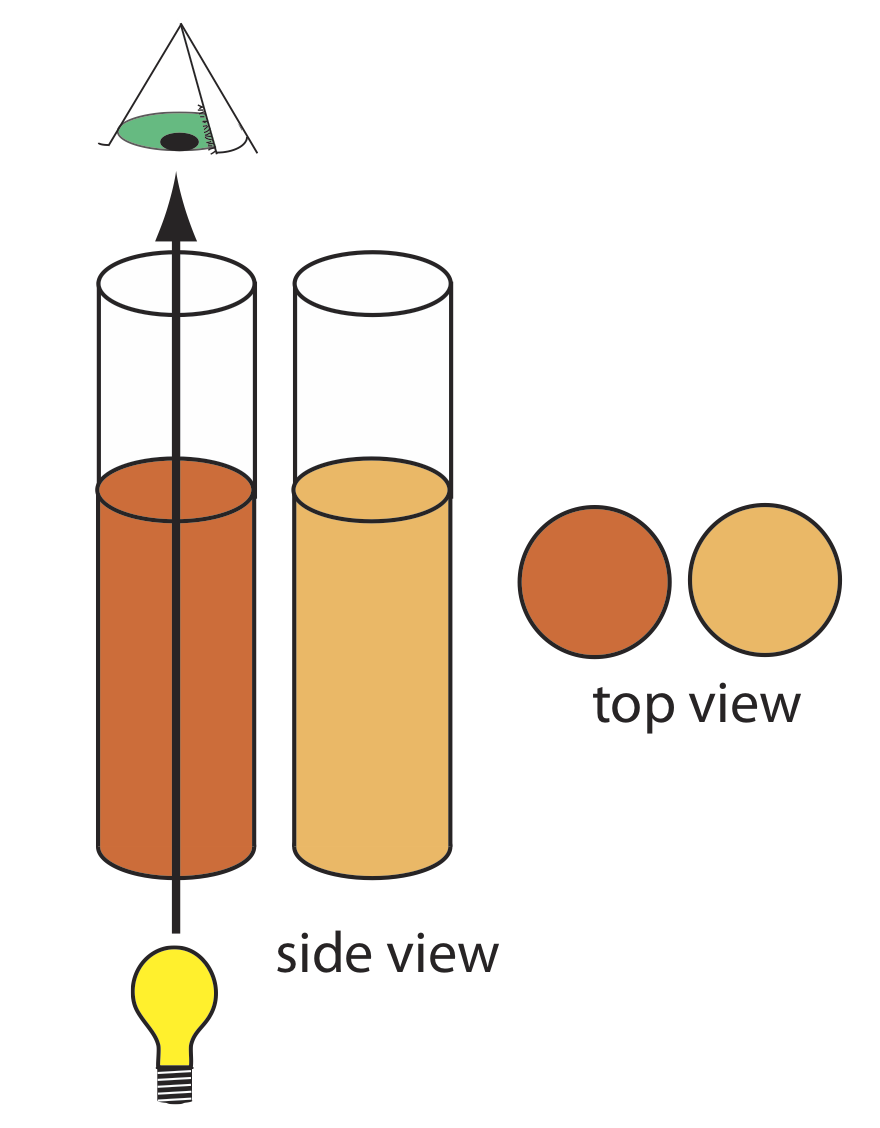
El método de Nessler convierte las propiedades químicas y/o físicas de una muestra, el color que se forma cuando NH ₃ reacciona con HgI ₂ y Ki, en una señal que podemos detectar, procesar y reportar como medida relativa de la cantidad de NH ₃ en la muestra. Aunque tal vez no pensemos en un tubo Nessler como un instrumento, el proceso de sondear una muestra de manera que convierta sus propiedades químicas o físicas en una forma de información que podamos reportar es la esencia de cualquier instrumento.

Los componentes básicos de un instrumento incluyen una sonda que interactúa con la muestra, un transductor de entrada que convierte las propiedades químicas y/o físicas de la muestra en una señal eléctrica, un procesador de señal que convierte la señal eléctrica en una forma que un transductor de salida puede convertir en un salida numérica o visual que podamos entender. Podemos representar esto como una secuencia de acciones que tienen lugar dentro del instrumento

\[\text{probe} \rightarrow \text{sample} \rightarrow \text{input transducer} \rightarrow \text{raw data} \rightarrow \text{signal processor} \rightarrow \text{output transducer} \nonumber \]

y como flujo general de información

\[\text{chemical and/or physical information} \rightarrow \text{electrical information} \rightarrow \text{numerical or visual response} \nonumber \]

En el método de Nessler, la sonda es la luz solar, el ojo del analista es el transductor de entrada, los datos brutos son la respuesta del nervio óptico del ojo a la atenuación de la luz, el procesador de señales es el cerebro y la salida es un informe visual del color de la muestra en relación con los estándares.

\[\text{sunlight} \rightarrow \text{sample} \rightarrow \text{eye} \rightarrow \text{response of optic never} \rightarrow \text{brain} \rightarrow \text{visual report of color} \nonumber \]

Formas de codificar la información

Como se sugirió anteriormente, la información se codifica de dos formas amplias: como información eléctrica (como corrientes y potenciales) y como información en otras formas no eléctricas (como las propiedades químicas y físicas).

Información no eléctrica

El método de Nessler comienza y termina con formas de información no eléctricas: la muestra tiene un color y usamos ese color para informar que la concentración de NH ₃ en nuestra muestra es mayor de 0.50 mg/L y menor de 1.00 mg/L. se forma precipitado cuando añadimos Ag ⁺ a una solución de NaCl, la báscula de barra de equilibrio que usa mi médico para medir mi peso, el porcentaje de luz que pasa por una muestra, y el volumen y moles de Cu (NO ₃) ₂ en un cilindro graduado.

Información Eléctrica

Aunque la balanza de mi médico codifica mi masa por la posición de dos pesos móviles a lo largo de un brazo de señal —un medio decididamente no eléctrico de codificación de información— la balanza analítica electrónica que se encuentra en casi todos los laboratorios de química codifica la masa en forma de información eléctrica (Figura \(\PageIndex{1}\)). Un electroimán levita el recipiente de muestra por encima de un imán cilíndrico permanente. Cuando colocamos un objeto en el recipiente de muestra, desplaza el recipiente de muestra hacia abajo por una fuerza igual al producto de la masa de la muestra y su aceleración debido a la gravedad. La balanza detecta este movimiento hacia abajo y genera una fuerza de contrapeso al aumentar la corriente al electroimán. La corriente necesaria para devolver el saldo a su posición original es proporcional a la masa del objeto.

Figura\(\PageIndex{1}\): La foto muestra una balanza electrónica típica capaz de determinar la masa al ±0.1 mg más cercano. La pegatina dentro del escudo contra el viento de la balanza es su certificación de calibración anual. Para una revisión de otros tipos de balanzas electrónicas, véase Schoonover, R. M. Anal. Chem. 1982, 54, 973A-980A.

Aunque tendemos a usar indistintamente, los términos “peso” y “masa”, existe una distinción importante entre ellos. La masa es la cantidad absoluta de materia en un objeto, medida en gramos. El peso, W, es una medida de la fuerza gravitacional, g, que actúa sobre esa masa, m:

\[W = m \times g \nonumber \]

Un objeto tiene una masa fija pero su peso depende de la aceleración debida a la gravedad, que varía sutilmente de una ubicación a otra.

Una balanza mide el peso de un objeto, no su masa. Debido a que el peso y la masa son proporcionales entre sí, podemos calibrar una balanza usando un peso estándar cuya masa es trazable al prototipo estándar para el kilogramo. Una balanza correctamente calibrada da un valor preciso para la masa de un objeto.

La información eléctrica viene en tres dominios: analógico, tiempo y digital. En el dominio analógico, la señal muestra la amplitud de la señal eléctrica, digamos corriente o potencial, en función de una variable independiente, que podría ser la longitud de onda al registrar un espectro, el potencial aplicado en un experimento de voltametría cíclica o el tiempo al separar una mezcla por cromatografía de gases. Una señal en el dominio del tiempo muestra la frecuencia con la que la señal eléctrica se eleva por encima o por debajo de un valor umbral, como al contar la velocidad a la que la radiación ionizante, como las partículas alfa o beta, son detectadas por un contador Geiger. Finalmente, en el dominio digital, la señal es un recuento de eventos discretos, como contar el número de gotas dispensadas por un autovalorador al permitir que las gotas interrumpan un haz de luz.

Transductores de entrada, detectores y sensores

Como se definió anteriormente, un transductor es un dispositivo que convierte la información de una forma no eléctrica a una forma eléctrica (el transductor de entrada) o de una forma eléctrica a una forma no eléctrica (el transductor de salida). Detector es un término mucho más amplio que incluye todos los aspectos del instrumento desde el transductor de entrada hasta el transductor de salida; así, un espectrómetro visible es un detector que utiliza un transductor de entrada para convertir la atenuación de la radiación fuente en una absorbancia reportada. Un sensor es un detector diseñado para monitorear un analito particular, tal como un electrodo de pH.

Transductores de salida y dispositivos de lectura

El transductor de salida de un instrumento convierte la información transportada en forma eléctrica en una forma no eléctrica que podemos entender. Ejemplos comunes de transductores de salida, o dispositivos de lectura, son un medidor simple, una pantalla digital, una traza física de la señal en función de una variable dependiente, como un espectro o un cromatograma, o una placa fotográfica.

Computadoras en Instrumentos

Muchos instrumentos incluyen una computadora que nos brinda la capacidad de controlar el instrumento y, quizás de mayor importancia, procesar los datos tanto modificando la señal eléctrica a medida que pasa del transductor de entrada al transductor de salida, como al proporcionar herramientas para procesar los datos después de él sale del transductor de salida.