1.5: Calibración de Métodos Instrumentales

Para estandarizar un método analítico también debemos determinar la sensibilidad del analito, k _A, en la siguiente ecuación

\[S_{total} = k_A C_A + S_{blank} \label{s_total} \]

donde\(S_{total}\) está la señal medida,\(C_A\) es la concentración del analito, y\(S_{reag}\) es la señal en ausencia del analito. En principio, es posible derivar el valor de k _A para cualquier método analítico si entendemos completamente todas las reacciones químicas y procesos físicos responsables de la señal. Desafortunadamente, tales cálculos no son factibles si carecemos de un modelo teórico suficientemente desarrollado de los procesos físicos o si la reacción química demuestra un comportamiento no ideal. En tales situaciones debemos determinar el valor de k _{A analizando una} o más soluciones estándar, cada una de las cuales contiene una cantidad conocida de analito. En esta sección consideramos varios enfoques para determinar el valor _de k A. Por simplicidad asumimos que\(S_{blank}\) es contabilizado por un blanco reactivo apropiado, lo que nos permite reemplazar S _total por la señal del analito, S _A.

\[S_A = k_A C_A \label{sa} \]

Estandarización de punto único frente a punto múltiple

La forma más sencilla de determinar el valor de k _A en la Ecuación\ ref {sa} es usar una estandarización de punto único en la que medimos la señal para un estándar, S _std, que contiene una concentración conocida de analito, C _std. Sustituir estos valores en Ecuación\ ref {sa} y reorganizar

\[k_A = \frac {S_{std}} {C_{std}} \label{ka} \]

_{para darnos el valor para k A.} Habiendo determinado k _A, podemos calcular la concentración de analito en una muestra midiendo su señal, S _samp, y calcular C _A como

\[C_A = \frac {S_{samp}} {k_A} \label{ca} \]

La estandarización de un solo punto es el método menos deseable para estandarizar un método. Hay dos razones para ello. Primero, cualquier error en nuestra determinación de k _A se traslada a nuestro cálculo _de C A. Segundo, nuestro valor experimental para k _A se basa en una sola concentración de analito. Para extender este valor de k _A a otras concentraciones de analito se requiere que asumamos una relación lineal entre la señal y la concentración del analito, suposición que muchas veces no es cierta [Cardone, M. J.; Palmero, P. J.; Sybrandt, L. B. Anal. Chem. 1980, 52, 1187—1191]. La figura\(\PageIndex{1}\) muestra cómo asumir un valor constante de k _A conduce a un error determinado en C _A si k _A se vuelve más pequeño a mayores concentraciones de analito. A pesar de estas limitaciones, las estandarizaciones de punto único encuentran uso rutinario cuando el rango esperado para las concentraciones del analito es pequeño. Bajo estas condiciones suele ser seguro asumir que k _A es constante (aunque se debe verificar esta suposición experimentalmente). Este es el caso, por ejemplo, en laboratorios clínicos donde muchos analizadores automatizados utilizan solo un único estándar.

Figura\(\PageIndex{1}\): Ejemplo que muestra cómo una estandarización de un solo punto conduce a un error determinado en la concentración reportada de un analito si asumimos incorrectamente que k _A es constante. La relación asumida entre S _samp y C _A se basa en un único estándar y es una línea recta; la relación real entre S _samp y C _A se curva para mayores concentraciones de analito.

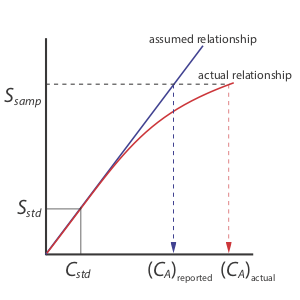
La mejor manera de estandarizar un método es preparar una serie de estándares, cada uno de los cuales contiene una concentración diferente de analito. Los estándares se eligen de tal manera que cortejan el rango esperado para la concentración del analito. Una estandarización de múltiples puntos debe incluir al menos tres estándares, aunque son preferibles más. Una gráfica de S _std versus C _std se llama curva de calibración. La estandarización exacta, o relación de calibración, está determinada por un algoritmo apropiado de ajuste de curvas.

La regresión lineal, que también se conoce como el método de mínimos cuadrados, es uno de esos algoritmos. Su uso está cubierto en el Apéndice 1.

Hay dos ventajas para una estandarización de múltiples puntos. Primero, aunque un error determinado en un estándar introduce un error determinado, su efecto es minimizado por los estándares restantes. Segundo, debido a que medimos la señal para varias concentraciones de analito, ya no debemos asumir que k _A es independiente de la concentración del analito. En cambio, podemos construir una curva de calibración similar a la “relación real” en la Figura\(\PageIndex{1}\).

Estándares externos

El método más común de estandarización utiliza uno o más estándares externos, cada uno de los cuales contiene una concentración conocida de analito. A estos estándares los llamamos “externos” porque se preparan y analizan separados de las muestras.

Agregar el adjetivo “externo” al sustantivo “estándar” podría parecerle extraño en este punto, ya que parece razonable suponer que los estándares y las muestras se analizan por separado. Como pronto aprenderemos, sin embargo, podemos agregar estándares a nuestras muestras y analizar ambas simultáneamente.

Estándar externo individual

Con un único estándar externo determinamos k _A usando eEquation\ ref {ka} y luego calculamos la concentración de analito, C _A, usando la Ecuación\ ref {ca}.

Ejemplo\(\PageIndex{1}\)

Un método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre produce una S _std de 0.474 para un único estándar para el cual la concentración de plomo es de 1.75 ppb. ¿Cuál es la concentración de Pb ^{2 +} en una muestra de sangre para la que S _samp es 0.361?

Solución

La ecuación\ ref {ka} nos permite calcular el valor de k _A usando los datos para el estándar externo único.

\[k_A = \frac {S_{std}} {C_{std}} = \frac {0.474} {1.75 \text{ ppb}} = 0.2709 \text{ ppb}^{-1} \nonumber \]

Habiendo determinado el valor de k _A, calculamos la concentración de Pb ^{2 +} en la muestra de sangre que se calcula utilizando la Ecuación\ ref {ca}.

\[C_A = \frac {S_{samp}} {k_A} = \frac {0.361} {0.2709 \text{ ppb}^{-1}} = 1.33 \text{ ppb} \nonumber \]

Múltiples estándares externos

La figura\(\PageIndex{2}\) muestra una típica estandarización externa de múltiples puntos. El matraz aforado de la izquierda contiene un blanco de reactivo y los matraces volumétricos restantes contienen concentraciones crecientes de Cu ^{2 +}. Debajo de los matraces volumétricos se muestra la curva de calibración resultante. Debido a que este es el método más común de estandarización, la relación resultante se denomina curva de calibración normal.

Figura\(\PageIndex{2}\): La foto en la parte superior de la figura muestra un blanco reactivo (extremo izquierdo) y un conjunto de cinco estándares externos para Cu ^{2 +} con concentraciones que aumentan de izquierda a derecha. Debajo de los estándares externos se muestra la curva de calibración normal resultante. La absorbancia de cada estándar, S _std, se muestra por los círculos rellenos.

Cuando una curva de calibración es una línea recta, como lo es en la Figura\(\PageIndex{2}\), la pendiente de la línea da el valor _de k A. Esta es la situación más deseable porque la sensibilidad del método permanece constante en todo el rango de concentración del analito. Cuando la curva de calibración no es una línea recta, la sensibilidad del método es una función de la concentración del analito. En la Figura\(\PageIndex{1}\), por ejemplo, el valor de k _A es mayor cuando la concentración del analito es pequeña y disminuye continuamente para mayores concentraciones de analito. El valor de k _A en cualquier punto a lo largo de la curva de calibración en la Figura\(\PageIndex{1}\) es la pendiente en ese punto. En cualquier caso, una curva de calibración permite relacionar la _{muestra de} S con la concentración del analito.

Ejemplo\(\PageIndex{2}\)

Un segundo método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre tiene una curva de calibración normal para la cual

\[S_{std} = (0.296 \text{ ppb}^{-1} \times C_{std}) + 0.003 \nonumber \]

¿Cuál es la concentración de Pb ^{2 +} en una muestra de sangre si S _samp es 0.397?

Solución

Para determinar la concentración de Pb ^{2 +} en la muestra de sangre, reemplazamos S _std en la ecuación de calibración con S _samp y resolvemos para C _A .

\[C_A = \frac {S_{samp} - 0.003} {0.296 \text{ ppb}^{-1}} = \frac {0.397 - 0.003} {0.296 \text{ ppb}^{-1}} = 1.33 \text{ ppb} \nonumber \]

Cabe señalar que la ecuación de calibración en este problema incluye un término extra que no aparece en la Ecuación\ ref {ca}. Idealmente esperamos que nuestra curva de calibración tenga una señal de cero cuando C _A es cero. Este es el propósito de usar un blanco reactivo para corregir la señal medida. El término extra de +0.003 en nuestra ecuación de calibración resulta de la incertidumbre en la medición de la señal para el reactivo en blanco y los estándares.

Una estandarización externa nos permite analizar una serie de muestras utilizando una sola curva de calibración. Esta es una ventaja importante cuando tenemos muchas muestras para analizar. No es sorprendente que muchos de los métodos analíticos cuantitativos más comunes utilicen una estandarización externa.

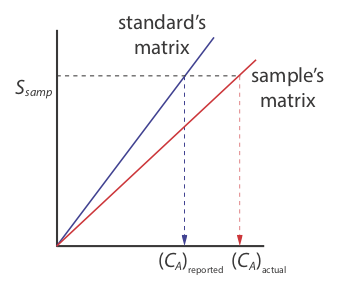
Existe una seria limitación, sin embargo, a una estandarización externa. Cuando determinamos el valor de k _A usando la Ecuación\ ref {ka}, el analito está presente en la matriz del estándar externo, que generalmente es una matriz mucho más simple que la de nuestras muestras. Cuando utilizamos una estandarización externa asumimos que la matriz no afecta el valor _de k A. Si esto no es cierto, entonces introducimos en nuestro análisis un error proporcional determinado. Este no es el caso en la Figura\(\PageIndex{3}\), por ejemplo, donde mostramos curvas de calibración para un analito en la matriz de la muestra y en la matriz del estándar. En este caso, el uso de la curva de calibración para los estándares externos conduce a un error negativo determinado en la concentración reportada del analito. Si esperamos que los efectos de matriz sean importantes, entonces intentamos hacer coincidir la matriz del estándar con la de la muestra, un proceso conocido como coincidencia de matrices. Si no estamos seguros de la matriz de la muestra, entonces debemos demostrar que los efectos matriciales son insignificantes o utilizar un método alternativo de estandarización. Ambos enfoques se discuten en la siguiente sección.

La matriz para los estándares externos en la Figura\(\PageIndex{2}\), por ejemplo, es amoníaco diluido. Debido a que el\(\ce{Cu(NH3)4^{2+}}\) complejo absorbe más fuertemente que Cu ^{2 +}, agregar amoníaco aumenta la magnitud de la señal. Si no conseguimos agregar la misma cantidad de amoníaco a nuestras muestras, entonces introduciremos un error proporcional determinado en nuestro análisis.

Figura\(\PageIndex{3}\): Curvas de calibración para un analito en la matriz del patrón y en la matriz de la muestra. Si la matriz afecta el valor de k _A, como es el caso aquí, entonces introducimos un error proporcional determinado en nuestro análisis si utilizamos una curva de calibración normal.

Adiciones estándar

Podemos evitar la complicación de emparejar la matriz de los estándares con la matriz de la muestra si realizamos la estandarización en la muestra. Esto se conoce como el método de adiciones estándar.

Adición Estándar Individual

La versión más simple de una adición estándar se muestra en la Figura\(\PageIndex{4}\). Primero agregamos una porción de la muestra, V _o, a un matraz aforado, la diluimos a volumen, V _f, y medimos su señal, S _samp. A continuación, agregamos una segunda porción idéntica de muestra a un matraz volumétrico equivalente junto con una espiga, V _std, de un estándar externo cuya concentración es C _std. Después de diluir la muestra enriquecida al mismo volumen final, medimos su señal, _pico S.

Figura\(\PageIndex{4}\): Ilustración que muestra el método de adiciones estándar. El matraz aforado de la izquierda contiene una porción de la muestra, V _o, y el matraz aforado de la derecha contiene una porción idéntica de la muestra y una espiga, V _std, de una solución estándar del analito. Ambos matraces se diluyen al mismo volumen final, V _f. La concentración de analito en cada matraz se muestra en la parte inferior de la figura donde C _A es la concentración del analito en la muestra original y C _std es la concentración de analito en el estándar externo.

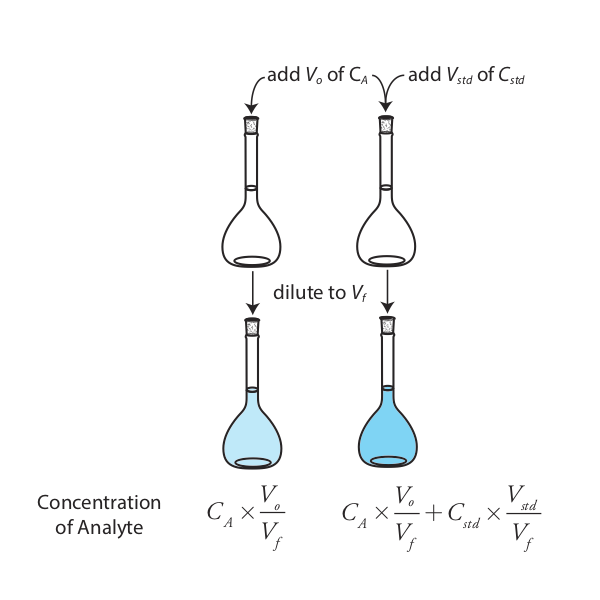
Las dos ecuaciones siguientes relacionan S _samp y S _spike con la concentración de analito, C _A, en la muestra original.

\[S_{samp} = k_A C_A \frac {V_o} {V_f} \label{sa_samp1} \]

\[S_{spike} = k_A \left( C_A \frac {V_o} {V_f} + C_{std} \frac {V_{std}} {V_f} \right) \label{sa_spike1} \]

Mientras V _std sea pequeño en relación con V _o, el efecto de la matriz del estándar sobre la matriz de la muestra es insignificante. Bajo estas condiciones el valor de k _A es el mismo en la Ecuación\ ref {sa_samp1} y la Ecuación\ ref {sa_spike1}. Resolver ambas ecuaciones para k _A y igualar da

\[\frac {S_{samp}} {C_A \frac {V_o} {V_f}} = \frac {S_{spike}} {C_A \frac {V_o} {V_f} + C_{std} \frac {V_{std}} {V_f}} \label{method_one} \]

que podemos resolver para la concentración de analito, C _A, en la muestra original.

Ejemplo\(\PageIndex{3}\)

Un tercer método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre produce una _muestra S de 0.193 cuando una muestra de sangre de 1.00 mL se diluye a 5.00 mL. A una segunda muestra de sangre de 1.00 mL se le agrega 1.00 mL de un estándar externo de 1560-ppb Pb ^{2 +} y se diluye a 5.00 mL, obteniéndose una _espiga S de 0.419. ¿Cuál es la concentración de Pb ^{2 +} en la muestra original de sangre?

Solución

_{Comenzamos haciendo las sustituciones apropiadas en la Ecuación\ ref {method_one} y resolviendo para C A.} Tenga en cuenta que todos los volúmenes deben estar en las mismas unidades; así, primero encubrimos V _std de 1.00 mL a\(1.00 \times 10^{-3} \text{ mL}\).

\[\frac {0.193} {C_A \frac {1.00 \text{ mL}} {5.00 \text{ mL}}} = \frac {0.419} {C_A \frac {1.00 \text{ mL}} {5.00 \text{ mL}} + 1560 \text{ ppb} \frac {1.00 \times 10^{-3} \text{ mL}} {5.00 \text{ mL}}} \nonumber \]

\[\frac {0.193} {0.200C_A} = \frac {0.419} {0.200C_A + 0.3120 \text{ ppb}} \nonumber \]

\[0.0386C_A + 0.0602 \text{ ppb} = 0.0838 C_A \nonumber \]

\[0.0452 C_A = 0.0602 \text{ ppb} \nonumber \]

\[C_A = 1.33 \text{ ppb} \nonumber \]

La concentración de Pb ^{2 +} en la muestra original de sangre es de 1.33 ppb.

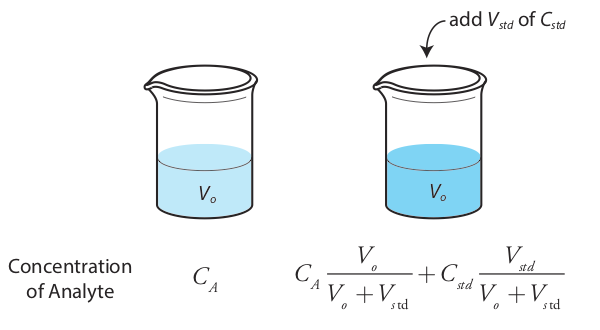
También es posible agregar la adición estándar directamente a la muestra, midiendo la señal tanto antes como después del pico (Figura\(\PageIndex{5}\)). En este caso el volumen final después de la adición estándar es V _o + V _std y la Ecuación\ ref {sa_samp1}, Ecuación\ ref {sa_spike1}, y Ecuación\ ref {method_one} convertido

\[S_{samp} = k_A C_A \label{sa_samp2} \]

\[S_{spike} = k_A \left( C_A \frac {V_o} {V_o + V_{std}} + C_{std} \frac {V_{std}} {V_o + V_{std}} \right) \label{sa_spike2} \]

\[\frac {S_{samp}} {C_A} = \frac {S_{spike}} {C_A \frac {V_o} {V_o + V_{std}} + C_{std} \frac {V_{std}} {V_o + V_{std}}} \label{method_two} \]

Figura\(\PageIndex{5}\): Ilustración que muestra una forma alternativa del método de adiciones estándar. En este caso agregamos el pico de estándar externo directamente a la muestra sin ningún ajuste adicional en el volumen.

Ejemplo\(\PageIndex{4}\)

Un cuarto método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre produce una _muestra de S de 0.712 para una muestra de sangre de 5.00 mL. Después de pinchar la muestra de sangre con 5.00 mL de un estándar externo Pb ^{2 +} de 1560-ppb, se mide una _espiga S de 1.546. ¿Cuál es la concentración de Pb ^{2 +} en la muestra original de sangre?

Solución

\[\frac {0.712} {C_A} = \frac {1.546} {C_A \frac {5.00 \text{ mL}} {5.005 \text{ mL}} + 1560 \text{ ppb} \frac {5.00 \times 10^{-3} \text{ mL}} {5.005 \text{ mL}}} \nonumber \]

\[\frac {0.712} {C_A} = \frac {1.546} {0.9990C_A + 1.558 \text{ ppb}} \nonumber \]

\[0.7113C_A + 1.109 \text{ ppb} = 1.546C_A \nonumber \]

\[C_A = 1.33 \text{ ppb} \nonumber \]

La concentración de Pb ^{2 +} en la muestra original de sangre es de 1.33 ppb.

Múltiples adiciones estándar

Podemos adaptar una adición estándar de punto único a una adición estándar de múltiples puntos preparando una serie de muestras que contienen cantidades crecientes del estándar externo. La figura\(\PageIndex{6}\) muestra dos formas de trazar una curva de calibración de adición estándar basada en la Ecuación\ ref {sa_spike1}. En la Figura\(\PageIndex{6}\) a representamos el _pico S contra el volumen de los picos, V _std. Si k _A es constante, entonces la curva de calibración es una línea recta. Es fácil demostrar que la intercepción x es equivalente a — C _A V _o/C _std.

Figura\(\PageIndex{6}\): En la parte superior de la figura se muestra un conjunto de seis adiciones estándar para la determinación de Mn ^{2 +}. El matraz de la izquierda es una muestra de 25.00 mL diluida a 50.00 mL con agua. Los matraces restantes contienen 25.00 mL de muestra y, de izquierda a derecha, 1.00, 2.00, 3.00, 4.00 y 5.00 mL espigas de un estándar externo que es 100.6 mg/L Mn ^{2 +}. A continuación se muestran dos formas de trazar la curva de calibración de adiciones estándar. La absorbancia para cada adición estándar, _pico S, se muestra por los círculos rellenos.

Ejemplo\(\PageIndex{5}\)

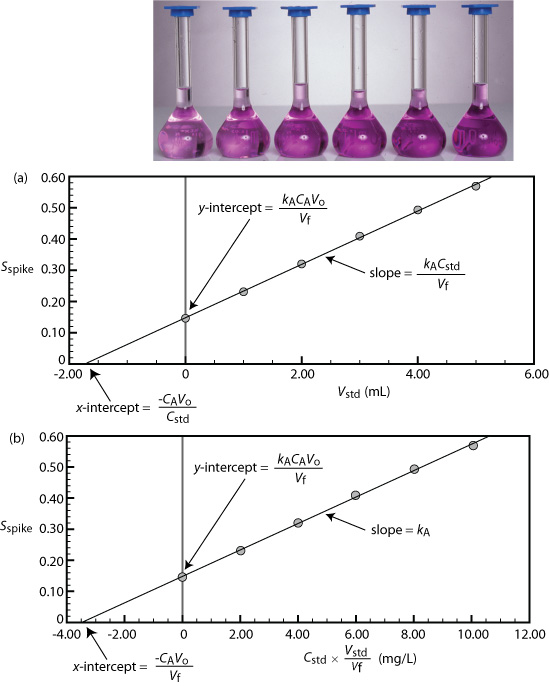
Comenzando con la Ecuación\ ref {sa_spike1} muestran que las ecuaciones en la Figura\(\PageIndex{6}\) a para la pendiente, la intercepción y y la intercepción x son correctas.

Solución

Comenzamos reescribiendo la ecuación\ ref {sa_spike1} como

\[S_{spike} = \frac {k_A C_A V_o} {V_f} + \frac {k_A C_{std}} {V_f} \times V_{std} \nonumber \]

que está en la forma de la ecuación para una línea recta

\[y = y\text{-intercept} + \text{slope} \times x\text{-intercept} \nonumber \]

donde y es _pico S y x es V _std. La pendiente de la línea, por lo tanto, es k _A C _std/V _f y la intercepción y es k _A C _A V _o/V _f. La intercepción x es el valor de x cuando y es cero, o

\[0 = \frac {k_A C_A V_o} {V_f} + \frac {k_A C_{std}} {V_f} \times x\text{-intercept} \nonumber \]

\[x\text{-intercept} = - \frac {k_A C_A V_o / V_f} {K_A C_{std} / V_f} = - \frac {C_A V_o} {C_{std}} \nonumber \]

Debido a que conocemos el volumen de la muestra original, V _o, y la concentración del estándar externo, C _std, podemos calcular las concentraciones del analito a partir de la intercepción x de adiciones estándar de múltiples puntos.

Ejemplo\(\PageIndex{6}\)

Un quinto método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre utiliza una adición estándar de múltiples puntos basada en la Ecuación\ ref {sa_spike1}. La muestra de sangre original tiene un volumen de 1.00 mL y el estándar utilizado para la adición de la muestra tiene una concentración de 1560 ppb Pb ^{2 +}. Todas las muestras se diluyeron a 5.00 mL antes de medir la señal. Una curva de calibración de _pico S versus V _std tiene la siguiente ecuación

\[S_{spike} = 0.266 + 312 \text{ mL}^{-1} \times V_{std} \nonumber \]

¿Cuál es la concentración de Pb ^{2 +} en la muestra original de sangre?

Solución

Para encontrar la intercepción x establecemos el _pico S igual a cero.

\[S_{spike} = 0.266 + 312 \text{ mL}^{-1} \times V_{std} \nonumber \]

Resolviendo para V _std, obtenemos un valor de\(-8.526 \times 10^{-4} \text{ mL}\) para la intercepción x. Sustituir el valor de la intercepción x en la ecuación de la Figura\(\PageIndex{6}\) a

\[-8.526 \times 10^{-4} \text{ mL} = - \frac {C_A V_o} {C_{std}} = - \frac {C_A \times 1.00 \text{ mL}} {1560 \text{ ppb}} \nonumber \]

y resolviendo para C _A da la concentración de Pb ^{2 +} en la muestra de sangre como 1.33 ppb.

Dado que construimos una curva de calibración de adiciones estándar en la muestra, no podemos usar la ecuación de calibración para otras muestras. Cada muestra, por lo tanto, requiere su propia curva de calibración de adiciones estándar. Esto es un serio inconveniente si tienes muchas muestras. Por ejemplo, supongamos que necesita analizar 10 muestras usando una curva de calibración de cinco puntos. Para una curva de calibración normal es necesario analizar solo 15 soluciones (cinco estándares y diez muestras). Si usas el método de adiciones estándar, sin embargo, debes analizar 50 soluciones (cada una de las diez muestras se analiza cinco veces, una vez antes de pinchar y después de cada una de las cuatro puntas).

Uso de una adición estándar para identificar efectos de matriz

Podemos usar el método de adiciones estándar para validar una estandarización externa cuando la coincidencia matricial no es factible. Primero, preparamos una curva de calibración normal de S _std versus C _std y determinamos el valor de k _A a partir de su pendiente. A continuación, preparamos una curva de calibración de adiciones estándar usando la ecuación\ ref {sa_spike1}, trazando los datos como se muestra en la Figura\(\PageIndex{6}\) b. _{La pendiente de esta curva de calibración de adiciones estándar proporciona una determinación independiente de k A.} Si no hay diferencia significativa entre los dos valores de k _A, entonces podemos ignorar la diferencia entre la matriz de la muestra y la de los estándares externos. Cuando los valores de k _A son significativamente diferentes, entonces el uso de una curva de calibración normal introduce un error proporcional determinado.

Estándares Internos

Para utilizar una estandarización externa o el método de adiciones estándar, debemos ser capaces de tratar de manera idéntica todas las muestras y estándares. Cuando esto no es posible, la exactitud y precisión de nuestra estandarización puede sufrir. Por ejemplo, si nuestro analito está en un disolvente volátil, entonces su concentración aumentará si perdemos disolvente por evaporación. Supongamos que tenemos una muestra y un patrón con concentraciones idénticas de analito y señales idénticas. Si ambos experimentan la misma pérdida proporcional de disolvente, entonces sus respectivas concentraciones de analito y señales permanecen idénticas. En efecto, podemos ignorar la evaporación si las muestras y los estándares experimentan una pérdida equivalente de disolvente. Sin embargo, si un patrón y una muestra idénticos pierden diferentes cantidades de disolvente, entonces sus respectivas concentraciones y señales ya no son iguales. En este caso no es posible una simple estandarización externa o adición estándar.

Todavía podemos completar una estandarización si hacemos referencia a la señal del analito a una señal de otra especie que agregamos a todas las muestras y estándares. La especie, que denominamos estándar interno, debe ser diferente al analito.

Debido a que el analito y el patrón interno reciben el mismo tratamiento, la relación de sus señales no se ve afectada por ninguna falta de reproducibilidad en el procedimiento. Si una solución contiene un analito de concentración C _A y un patrón interno de concentración C _IS, entonces las señales debidas al analito, S _A, y el patrón interno, S _IS, son

\[S_A = k_A C_A \nonumber \]

\[S_{IS} = k_{SI} C_{IS} \nonumber \]

donde\(k_A\) y\(k_{IS}\) son las sensibilidades para el analito y el estándar interno, respectivamente. Tomando la relación de las dos señales da la ecuación fundamental para una estandarización interna.

\[\frac {S_A} {S_{IS}} = \frac {k_A C_A} {k_{IS} C_{IS}} = K \times \frac {C_A} {C_{IS}} \label{sa_sis} \]

Debido a que K es una relación entre la sensibilidad del analito y la sensibilidad del estándar interno, no es necesario determinar independientemente los valores para k _A o k _IS.

Estándar interno único

En una estandarización interna de un solo punto, preparamos un único estándar que contiene el analito y el estándar interno, y lo usamos para determinar el valor de K en la Ecuación\ ref {sa_sis}.

\[K = \left( \frac {C_{IS}} {C_A} \right)_{std} \times \left( \frac {S_A} {S_{IS}} \right)_{std} \label{K} \]

Una vez estandarizado el método, la concentración del analito viene dada por

\[C_A = \frac {C_{IS}} {K} \times \left( \frac {S_A} {S_{IS}} \right)_{samp} \nonumber \]

Ejemplo\(\PageIndex{7}\)

Un sexto método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre utiliza Cu ^{2 +} como estándar interno. Un estándar que es 1.75 ppb Pb ^{2 +} y 2.25 ppb Cu ^{2 +} produce una relación de (S _A/S _IS) _std de 2.37. Una muestra de sangre enriquecida con la misma concentración de Cu ^{2 +} da una relación señal, (S _A/S _IS) _samp, de 1.80. ¿Cuál es la concentración de Pb ^{2 +} en la muestra de sangre?

Solución

La ecuación\ ref {K} nos permite calcular el valor de K usando los datos para el estándar

\[K = \left( \frac {C_{IS}} {C_A} \right)_{std} \times \left( \frac {S_A} {S_{IS}} \right)_{std} = \frac {2.25 \text{ ppb } \ce{Cu^{2+}}} {1.75 \text{ ppb } \ce{Pb^{2+}}} \times 2.37 = 3.05 \frac {\text{ppb } \ce{Cu^{2+}}} {\text{ppb } \ce{Pb^{2+}}} \nonumber \]

La concentración de Pb ^{2 +}, por lo tanto, es

\[C_A = \frac {C_{IS}} {K} \times \left( \frac {S_A} {S_{IS}} \right)_{samp} = \frac {2.25 \text{ ppb } \ce{Cu^{2+}}} {3.05 \frac {\text{ppb } \ce{Cu^{2+}}} {\text{ppb } \ce{Pb^{2+}}}} \times 1.80 = 1.33 \text{ ppb } \ce{Pb^{2+}} \nonumber \]

Múltiples Estándares Internos

Una estandarización interna de un solo punto tiene las mismas limitaciones que una calibración normal de un solo punto. Para construir una curva de calibración patrón interno preparamos una serie de patrones, cada uno de los cuales contiene la misma concentración de patrón interno y diferentes concentraciones de analito. Bajo estas condiciones una curva de calibración de (S _A/S _IS) _std versus C _A es lineal con una pendiente de K/C _IS .

Si bien la práctica habitual es preparar los estándares para que cada uno contenga una cantidad idéntica de la norma interna, esto no es un requisito.

Ejemplo\(\PageIndex{8}\)

Un séptimo método espectrofotométrico para el análisis cuantitativo de Pb ^{2 +} en sangre proporciona una curva de calibración lineal de patrones internos para la cual

\[\left( \frac {S_A} {S_{IS}} \right)_{std} = (2.11 \text{ ppb}^{-1} \times C_A) - 0.006 \nonumber \]

¿Cuál es el ppb Pb ^{2 +} en una muestra de sangre si (S _A/S _IS) _samp es 2.80?

Solución

Para determinar la concentración de Pb ^{2 +} en la muestra de sangre reemplazamos (S _A/S _IS) _std en la ecuación de calibración por (S _A/ S _IS) _samp y soluciona para C _A.

\[C_A = \frac {\left( \frac {S_A} {S_{IS}} \right)_{samp} + 0.006} {2.11 \text{ ppb}^{-1}} = \frac {2.80 + 0.006} {2.11 \text{ ppb}^{-1}} = 1.33 \text{ ppb } \ce{Pb^{2+}} \nonumber \]

La concentración de Pb ^{2 +} en la muestra de sangre es de 1.33 ppb.

En algunas circunstancias no es posible preparar los estándares para que cada uno contenga la misma concentración de estándar interno. Este es el caso, por ejemplo, cuando preparamos muestras por masa en lugar de volumen. Todavía podemos preparar una curva de calibración, sin embargo, trazando\((S_A / S_{IS})_{std}\) versus C _A/C _IS, dando una curva de calibración lineal con una pendiente de K.

Quizás se pregunte si es posible incluir un estándar interno en el método de adiciones estándar para corregir tanto los efectos de la matriz como las variaciones incontroladas entre muestras; bueno, la respuesta es sí como se describe en el artículo “Análisis de dilución estándar”, cuya referencia completa es Jones, W. B. Donati, G. L.; Calloway, C. P.; Jones, B. T. Anal. Chem. 2015, 87, 2321-2327.