1.4: Selección de un Método Analítico
- Page ID
- 78758
El análisis de una muestra genera una señal química o física que es proporcional a la cantidad de analito en la muestra. Esta señal puede ser cualquier cosa que podamos medir, como los ejemplos descritos en la Sección 1.2. Es conveniente dividir las técnicas analíticas en dos clases generales en función de si la señal es directamente proporcional a la masa o moles de analito, o es directamente proporcional a la concentración del analito.
Considera los dos cilindros graduados en la Figura\(\PageIndex{1}\), cada uno de los cuales contiene una solución de 0.010 M Cu (NO 3) 2. El cilindro de la izquierda contiene 10 mL, o\(1.0 \times 10^{-4}\) moles de Cu 2 +, y el cilindro de la derecha contiene 20 mL, o\(2.0 \times 10^{-4}\) moles de Cu 2 +. Si una técnica responde a la cantidad absoluta de analito en la muestra, entonces la señal debida al analito S A se da como
\[S_A = k_A n_A \label{totalanalysis} \]
donde n A son los moles o gramos de analito en la muestra, y k A es una constante de proporcionalidad. Debido a que el cilindro de la derecha contiene el doble de moles de Cu 2 + que el cilindro de la izquierda, analizar su contenido da una señal dos veces más grande que la del otro cilindro.
Una segunda clase de técnicas analíticas son aquellas que responden a la concentración del analito, C A
\[S_A = k_A C_A \label{concanalysis} \]
En este caso, un análisis del contenido de los dos cilindros da el mismo resultado. Como la mayoría de los instrumentos responden a la concentración del analito, nos comprometiremos a usar la Ecuación\ ref {concanálisis} para el resto de esta sección.
Definir el problema
Para seleccionar un método analítico adecuado para un problema particular necesitamos considerar nuestras necesidades y compararlas con las fortalezas y debilidades de los métodos analíticos disponibles. Si estamos analizando muestras en una línea de producción para determinar si un analito excede un umbral para que podamos dejarlas a un lado para un análisis más cuidadoso, entonces es posible que deseemos dar más consideración a la velocidad que a la precisión o precisión. Por otro lado, si nuestro analito es parte de una mezcla compleja, entonces tal vez deseemos dar más consideración a métodos analíticos que proporcionen mayor selectividad. O bien, si esperamos que nuestras muestras varíen sustancialmente en la concentración de analito, entonces podemos dar más consideración a un método analítico para el cual la Ecuación\ ref {concanálisis} se aplica en un amplio rango de concentraciones.
Características de rendimiento de los instrumentos
Como se sugirió anteriormente, cuando elegimos un método analítico, hacemos coincidir sus características de desempeño (o cifras de mérito) a nuestras necesidades. Algunas de estas características son cuantitativas (precisión, precisión, sensibilidad, límite de detección, selectividad, rango dinámico y selectividad) y otras son más cualitativas (robustez, robustez, escala de operación, tiempo y costo).
Precisión
La precisión, o sesgo, es una medida de lo cerca que está el resultado de un experimento del resultado “verdadero” o esperado. Podemos expresar la precisión como un error absoluto, e
\[e = x - \mu \nonumber \]
donde\(x\) está el resultado experimental y\(\mu\) es el resultado esperado, o como porcentaje de error relativo,% e r
\[\% e_r = \frac {x - \mu} {\mu} \times 100 \nonumber \]
La precisión de un método depende de muchas cosas, incluyendo la fuente de la señal, el valor de k A en la Ecuación\ ref {concanálisis} y la facilidad de manejo de muestras sin pérdida ni contaminación.
Debido a que es poco probable que sepamos el resultado verdadero, podemos usar un resultado esperado o aceptado para evaluar la precisión. Por ejemplo, podríamos usar un material de referencia estándar, que tiene un valor aceptado para nuestro analito, para establecer la precisión del método analítico. Encontrará un tratamiento más detallado de la precisión en, incluyendo una discusión de fuentes de errores, en el Apéndice 1.
Precisión
Cuando analizamos una muestra varias veces, los resultados individuales varían de un ensayo a otro. La precisión es una medida de esta variabilidad. Cuanto más cerca esté la concordancia entre los análisis individuales, más precisos serán los resultados. Por ejemplo, los resultados mostrados en la mitad superior de la Figura\(\PageIndex{2}\) para la concentración de potasio en una muestra de suero son más precisos que los de la mitad inferior de la Figura\(\PageIndex{2}\). Es importante entender que la precisión no implica exactitud. Que los datos en la mitad superior de la Figura\(\PageIndex{2}\) sean más precisos no significa que el primer conjunto de resultados sea más preciso. De hecho, ninguno de los dos conjuntos de resultados puede ser exacto.
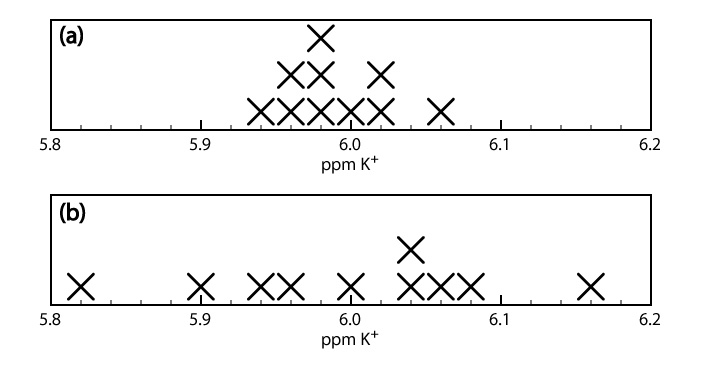
La precisión de un método depende de varios factores, incluyendo la incertidumbre en la medición de la señal y la facilidad de manejo de las muestras de manera reproducible, y se reporta como una desviación estándar absoluta, s
\[s = \sqrt{\frac {\sum_{i = 1}^{n} (X_i - \overline{X})^{2}} {n - 1}} \label{sd} \]
o una desviación estándar relativa, s r
\[s_r = \frac {s} {\overline{X}} \label{rsd} \]
donde\(\overline{X}\) es el promedio, o valor medio de las mediciones individuales.
\[\overline{X} = \frac {\sum_{i = 1}^n X_i} {n} \label{mean} \]
Confundir precisión y precisión es un error común. Ver Ryder, J.; Clark, A. U. Chem. Ed. 2002, 6, 1—3, y Tomlinson, J.; Dyson, P. J.; Garratt, J. U. Chem. Ed. 2001, 5, 16—23 para discusiones sobre este y otros conceptos erróneos comunes sobre el significado del error. Encontrará un tratamiento más detallado de la precisión en el Apéndice 1, incluyendo una discusión de fuentes de errores.
Sensibilidad
La capacidad de demostrar que dos muestras tienen diferentes cantidades de analito es una parte esencial de muchos análisis. La sensibilidad de un método es una medida de su capacidad para establecer que tal diferencia es significativa. La sensibilidad a menudo se confunde con el límite de detección de un método, que es la menor cantidad de analito que podemos determinar con confianza.
Véase Pardue, H. L. Clin. Chem. 1997, 43, 1831-1837 para una explicación de por qué la sensibilidad de un método no es lo mismo que su límite de detección.
La sensibilidad es equivalente a la constante de proporcionalidad, k A, en la Ecuación\ ref {concanálisis} [IUPAC Compendio de Terminología Química, Versión electrónica]. Si\(\Delta S_A\) es la diferencia más pequeña que podemos medir entre dos señales, entonces la diferencia más pequeña detectable en la concentración del analito es
\[\Delta C_A = \frac {\Delta S_A} {k_A} \nonumber \]
Supongamos, por ejemplo, que nuestra señal analítica es una medida para la cual el menor incremento detectable es ±0.001 (unidades arbitrarias). Si la sensibilidad de nuestro método es\(0.200 \text{M}^{-1}\), entonces nuestro método puede detectar posiblemente una diferencia en la concentración de tan poco como
\[\Delta C_A = \frac {\pm 0.001 } {0.200 \text{ M}^{-1}} = \pm 0.005 \text{ M}^{-1} \nonumber \]
Para dos métodos con el mismo\(\Delta S_A\), el método con mayor sensibilidad, es decir, el método con la k A más grande, es mejor capaz de discriminar entre cantidades menores de analito.
Límite de detección
La Unión Internacional de Química Pura y Aplicada (IUPAC) define el límite de detección de un método como la concentración más pequeña o cantidad absoluta de analito que tiene una señal significativamente mayor que la señal de un blanco adecuado [IUPAC Compendio de Tecnología Química, Versión Electrónica]. Si bien nuestro interés está en la cantidad de analito, en esta sección definiremos el límite de detección en términos de la señal del analito. Conociendo la señal, podemos calcular la concentración del analito, C A, usando la Ecuación\ ref {concanálisis},\(S_A = k_A C_A\) donde k es la sensibilidad del método.
Traduzcamos la definición IUPAC del límite de detección a una forma matemática dejando que S mb represente la señal promedio para un método en blanco, y dejando\(\sigma_{mb}\) representar la desviación estándar del blanco del método. Para detectar el analito, su señal debe exceder de S mb en una cantidad adecuada; así,
\[(S_A)_{DL} = S_{mb} \pm z \sigma_{mb} \label{detlimit} \]
donde\((S_A)_{DL}\) está el límite de detección del analito.
El valor que elegimos para z depende de nuestra tolerancia para reportar la concentración del analito aunque esté ausente de la muestra (lo que se llama error tipo 1). Normalmente, z se establece en tres, lo que corresponde a una probabilidad,\(\alpha\), de 0.00135, o 0.135%. Como se muestra en la Figura\(\PageIndex{3}\) a, solo hay un 0.135% de probabilidad de detectar el analito en una muestra que realmente está libre de analito.
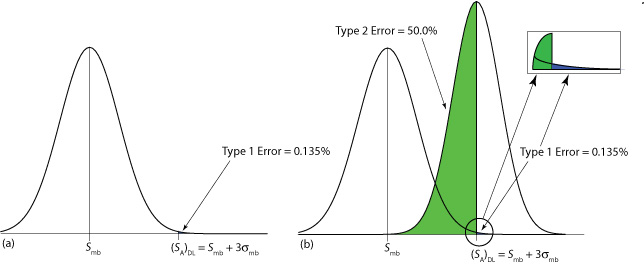
Un límite de detección también está sujeto a un error tipo 2 en el que no encontramos evidencia del analito aunque esté presente en la muestra. Consideremos, por ejemplo, la situación que se muestra en la Figura\(\PageIndex{3}\) b donde la señal para una muestra que contiene el analito es exactamente igual a (S A) DL. En este caso la probabilidad de un error tipo 2 es del 50% porque la mitad de las señales posibles de la muestra están por debajo del límite de detección. Detectamos correctamente el analito en el límite de detección de la IUPAC solo la mitad del tiempo. La definición de IUPAC para el límite de detección es la señal más pequeña para la que podemos decir, a un nivel de significancia de\(\alpha\), que un analito está presente en la muestra; sin embargo, no detectar el analito no significa que no esté presente en la muestra.
El límite de detección a menudo se representa, particularmente cuando se discuten temas de política pública, como una línea distinta que separa las concentraciones detectables de analitos de las concentraciones que no podemos detectar. Este uso de un límite de detección es incorrecto [Rogers, L. B. J. Chem. Educ. 1986, 63, 3—6]. Como sugiere la Figura\(\PageIndex{3}\), para un analito cuya concentración está cerca del límite de detección existe una alta probabilidad de que no detectemos el analito.
Una expresión alternativa para el límite de detección, el límite de identificación, minimiza tanto los errores tipo 1 como tipo 2 [Long, G. L.; Winefordner, J. D. Anal. Chem. 1983, 55, 712A—724A]. La señal del analito en el límite de identificación, (S A) LOI, incluye un término adicional,\(z \sigma_A\), para dar cuenta de la distribución de la señal del analito.
\[(S_A)_\text{LOI} = (S_A)_\text{DL} + z \sigma_A = S_{mb} + z \sigma_{mb} + z \sigma_A \label{loi} \]
Como se muestra en la Figura\(\PageIndex{4}\), el límite de identificación proporciona una probabilidad igual de un error de tipo 1 y de tipo 2 en el límite de detección. Cuando la concentración del analito está en su límite de identificación, solo hay un 0.135% de probabilidad de que su señal sea indistinguible de la del método blanco.
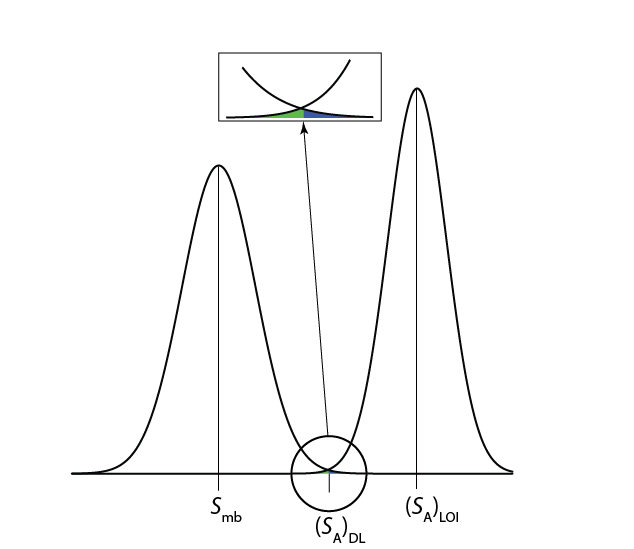
La capacidad de detectar el analito con confianza no es la misma que la capacidad de reportar con confianza su concentración, o de distinguir entre su concentración en dos muestras. Por esta razón el Comité de Química Analítica Ambiental de la Sociedad Americana de Química Química recomienda el límite de cuantificación, (S A) LOQ [“Lineamientos para la Adquisición de Datos y Evaluación de la Calidad de Datos en Química Ambiental”, Anal. Chem. 1980, 52, 2242—2249].
\[(S_A)_\text{LOQ} = S_{mb} + 10 \sigma_{mb} \label{loq} \]
Rango Dinámico
El rango dinámico (o rango lineal) de un método va desde su límite de cuantización, (Ecuación\ ref {loq}, hasta la concentración más alta para la que la sensibilidad, k A, permanece constante, dando como resultado una relación lineal entre\(S_A\) y\(C_A\). Este límite superior se llama el límite de linealidad, jajaja. Entre el LOQ y el LOL podemos usar la Ecuación\ ref {concanálisis} para convertir una señal medida en la concentración correspondiente del analito. Por encima del LOQ la relación entre la señal y la concentración del analito ya no es una línea recta.
Selectividad
Un método analítico es específico si su señal depende únicamente del analito [Persson, B-A; Vessman, J. Trends Anal. Chem. 1998, 17, 117—119; Persson, B-A; Vessman, J. Tendencias Anal. Chem. 2001, 20, 526—532]. Aunque la especificidad es lo ideal, pocos métodos analíticos están libres de interferencias. Cuando un interferente, I, contribuye a la señal, expandimos\ ref {totalanalysis} y Ecuación\ ref {concanálisis} para incluir su contribución a la señal de la muestra, S samp
\[S_{samp} = S_A + S_I = k_A C_A + k_I C_I \label{concsamp} \]
donde S I es la contribución del interferente a la señal, k I es la sensibilidad del interferente y C I es la concentración de interferente en la muestra.
La selectividad es una medida de la ausencia de interferencias de un método [Valcárcel, M.; Gomez-Hens, A.; Rubio, S. Trends Anal. Chem. 2001, 20, 386—393]. La selectividad de un método para un interferente en relación con el analito se define por un coeficiente de selectividad, K A, I
\[K_{A,I} = \frac {k_I} {k_A} \label{selectcoef} \]
que puede ser positivo o negativo dependiendo de los signos de k I y k A. El coeficiente de selectividad es mayor que +1 o menor que —1 cuando el método es más selectivo para el interferente que para el analito.
Aunque k A y k I suelen ser positivos, pueden ser negativos. Por ejemplo, algunos métodos analíticos funcionan midiendo la concentración de una especie que queda después de que reacciona con el analito. A medida que aumenta la concentración del analito, la concentración de la especie que produce la señal disminuye y la señal se vuelve más pequeña. Si a la señal en ausencia de analito se le asigna un valor de cero, entonces las señales posteriores son negativas.
Determinar el valor del coeficiente de selectividad es fácil si ya conocemos los valores para k A y k I. Como se muestra en Ejemplo\(\PageIndex{1}\), también podemos determinar K A, I midiendo S samp en presencia y en ausencia del interferente.
Un método para el análisis de Ca 2 + en agua sufre de una interferencia en presencia de Zn 2 +. Cuando la concentración de Ca 2 + es 100 veces mayor que la de Zn 2 +, un análisis para Ca 2 + tiene un error relativo de +0.5%. ¿Cuál es el coeficiente de selectividad para este método?
Solución
Dado que solo se reportan concentraciones relativas, podemos asignar arbitrariamente concentraciones absolutas. Para facilitar los cálculos, dejaremos que C Ca = 100 (unidades arbitrarias) y C Zn = 1. Un error relativo de +0.5% significa que la señal en presencia de Zn 2 + es 0.5% mayor que la señal en ausencia de Zn 2 +. Nuevamente, podemos asignar valores para facilitar el cálculo. Si la señal para Cu 2 + en ausencia de Zn 2 + es de 100 (unidades arbitrarias), entonces la señal en presencia de Zn 2 + es 100.5.
El valor de k Ca se determina usando la ecuación\ ref {concanálisis}
\[k_\text{Ca} = \frac {S_\text{Ca}} {C_\text{Ca}} = \frac {100} {100} = 1 \nonumber \]
En presencia de Zn 2 + la señal viene dada por la Ecuación\ ref {concsamp}; así
\[S_{samp} = 100.5 = k_\text{Ca} C_\text{Ca} + k_\text{Zn} C_\text{Zn} = (1 \times 100) + k_\text{Zn} \times 1 \nonumber \]
Resolver para k Zn da su valor como 0.5. El coeficiente de selectividad es
\[K_\text{Ca,Zn} = \frac {k_\text{Zn}} {k_\text{Ca}} = \frac {0.5} {1} = 0.5 \nonumber \]
Si no está seguro de por qué, en el ejemplo anterior, la señal en presencia de zinc es 100.5, tenga en cuenta que el porcentaje de error relativo para este problema viene dado por
\[\frac {\text{obtained result} - 100} {100} \times 100 = +0.5 \% \nonumber \]
Resolver da un resultado obtenido de 100.5.
Un coeficiente de selectividad nos proporciona una manera útil de evaluar el efecto potencial de un interferente en un análisis. Resolviendo Ecuación\ ref {selectcoef} para k I
\[k_I = K_{A,I} \times k_A \label{ki} \]
y sustituyendo en Ecuación\ ref {concanálisis} y simplificando da
\[S_{samp} = k_A \{ C_A + K_{A,I} \times C_I \} \label{S_samp} \]
Un interferente no planteará ningún problema siempre y cuando el término\(K_{A,I} \times C_I\) en la Ecuación\ ref {s_SAMP} sea significativamente menor que C A.
Barnett y sus colegas desarrollaron un método para determinar la concentración de codeína (estructura que se muestra a continuación) en plantas de amapola [Barnett, N. W.; Bowser, T. A.; Geraldi, R. D.; Smith, B. Anal. Chim. Acta 1996, 318, 309— 317]. Como parte de su estudio evaluaron el efecto de varios interferentes. Por ejemplo, los autores encontraron que las soluciones equimolares de codeína y la 6-metoxicodeína interferente dieron señales, respectivamente de 40 y 6 (unidades arbitrarias).
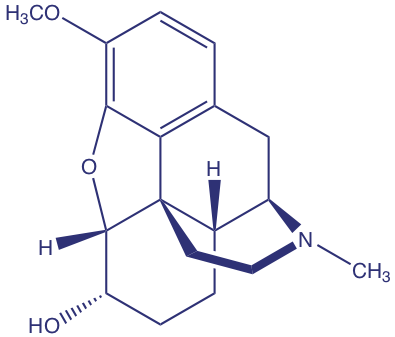
(a) Cuál es el coeficiente de selectividad para el interferente, 6-metoxicodeína, relativo al del analito, codeína.
(b) Si necesitamos conocer la concentración de codeína con una precisión de ± 0.50%, ¿cuál es la concentración relativa máxima de 6-metoxi-codeína que podemos tolerar?
Solución
(a) Las señales debidas al analito, S A, y al interferente, S I, son
\[S_A = k_A C_A \quad \quad S_I = k_I C_I \nonumber \]
Resolver estas ecuaciones para k A y para k I, y sustituyendo en Ecuación\ ref {selectcoef} da
\[K_{A,I} = \frac {S_I / C_I} {S_A / C_I} \nonumber \]
Debido a que las concentraciones de analito e interferente son equimolares (C A = C I), el coeficiente de selectividad es
\[K_{A,I} = \frac {S_I} {S_A} = \frac {6} {40} = 0.15 \nonumber \]
b) Para lograr una precisión superior a ± 0.50% el término\(K_{A,I} \times C_I\) en la Ecuación\ ref {s_SAMP} debe ser inferior al 0.50% de C A; así
\[K_{A,I} \times C_I \le 0.0050 \times C_A \nonumber \]
Resolviendo esta desigualdad para la relación C I/C A y sustituyendo en el valor de K A, I de la parte (a) da
\[\frac {C_I} {C_A} \le \frac {0.0050} {K_{A,I}} = \frac {0.0050} {0.15} = 0.033 \nonumber \]
Por lo tanto, la concentración de 6-metoxicodeína debe ser inferior al 3.3% de la concentración de codeína.
Los problemas de selectividad también son más probables cuando el analito está presente a una concentración muy baja [Rodgers, L. B. J. Chem. Educ. 1986, 63, 3—6].
Robustez y robustez
Para que un método sea útil debe proporcionar resultados confiables. Desafortunadamente, los métodos están sujetos a una variedad de interferencias químicas y físicas que aportan incertidumbre al análisis. Si un método está relativamente libre de interferencias químicas, podemos usarlo para analizar un analito en una amplia variedad de matrices de muestra. Dichos métodos se consideran robustos.
Las variaciones aleatorias en condiciones experimentales introducen incertidumbre. Si la sensibilidad de un método, k, depende demasiado de las condiciones experimentales, como la temperatura, la acidez o el tiempo de reacción, entonces un ligero cambio en cualquiera de estas condiciones puede dar un resultado significativamente diferente. Un método robusto es relativamente insensible a los cambios en las condiciones experimentales.
Escala de Operación
Otra forma de reducir la elección de métodos es considerar tres limitaciones potenciales: la cantidad de muestra disponible para el análisis, la concentración esperada de analito en las muestras y la cantidad mínima de analito que producirá una señal medible. Colectivamente, estas limitaciones definen la escala de operaciones del método analítico.
Podemos mostrar visualmente la escala de operaciones (Figura\(\PageIndex{5}\)) trazando el tamaño de la muestra en el eje x y la concentración del analito en el eje y. Para mayor comodidad, dividimos las muestras en <0.1 mg) sizes, and we divide analytes into major (> componentes macro (>0.1 g), meso (10 mg—100 mg), micro (0.1 mg—10 mg) y ultramicro (1% w/w), menor (0.01% w/w— 1% w/w), traza (10-7% w/w— 0.01% w/w) y ultratrace (<10 —7% w/w). En conjunto, la concentración del analito y el tamaño de la muestra proporcionan una descripción característica para un análisis. Por ejemplo, en un análisis de microtrazas la muestra pesa entre 0.1 mg y 10 mg y contiene una concentración de analito entre 10 —7% w/w y 10 —2% w/w.
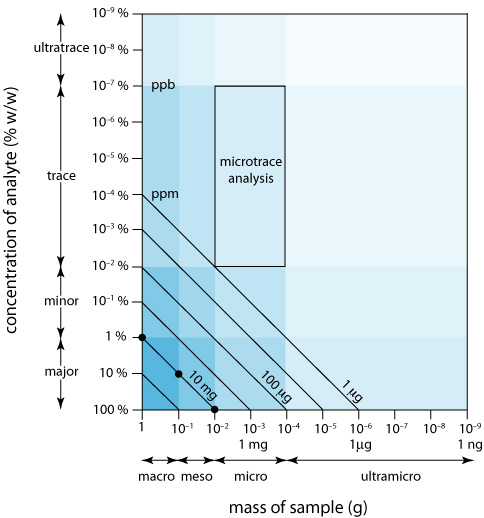
Las líneas diagonales que conectan los ejes muestran combinaciones de tamaño de muestra y concentración de analito que contienen la misma masa absoluta de analito. Como se muestra en la Figura\(\PageIndex{5}\), por ejemplo, una muestra de 1 g que es 1% p/p de analito tiene la misma cantidad de analito (10 mg) que una muestra de 100 mg que es 10% p/p de analito, o una muestra de 10 mg que es 100% p/p de analito.
Podemos usar Figura\(\PageIndex{5}\) para establecer límites para los métodos analíticos. Si la señal mínima detectable de un método es equivalente a 10 mg de analito, entonces es la más adecuada para un analito mayor en una muestra macro o meso. Extender el método a un analito con una concentración de 0.1% w/w requiere una muestra de 10 g, lo que rara vez es práctico debido a las complicaciones de llevar una cantidad tan grande de material a través del análisis. Por otro lado, una pequeña muestra que contiene una cantidad traza de analito impone restricciones significativas a un análisis. Por ejemplo, una muestra de 1 mg que es 10 —4% w/w en analito contiene solo 1 ng de analito. Si aislamos el analito en 1 mL de solución, entonces necesitamos un método analítico que de manera confiable pueda detectarlo a una concentración de 1 ng/mL.
Equipo, Tiempo y Costo
Finalmente, podemos comparar los métodos analíticos con respecto a sus necesidades de equipo, el tiempo necesario para completar un análisis y el costo por muestra. Los métodos que dependen de la instrumentación requieren un uso intensivo de equipos y pueden requerir una capacitación significativa del operador. Por ejemplo, el método espectroscópico de absorción atómica del horno de grafito para determinar el plomo en el agua requiere una importante inversión de capital en el instrumento y un operador experimentado para obtener resultados confiables. Otros métodos, como la titrimetría, requieren equipos menos costosos y menos capacitación.
El tiempo para completar un análisis para una muestra a menudo es bastante similar de método a método. Esto es algo engañoso, sin embargo, porque gran parte de este tiempo se dedica a preparar muestras, preparar reactivos y reunir equipos. Una vez que las muestras, los reactivos y el equipo están en su lugar, la velocidad de muestreo puede diferir sustancialmente. Por ejemplo, solo se necesitan unos minutos para analizar una sola muestra para plomo usando espectroscopía de absorción atómica de horno de grafito, pero varias horas para analizar la misma muestra usando gravimetría. Esto es un factor significativo en la selección de un método para un laboratorio que maneja un alto volumen de muestras.
El costo de un análisis depende de muchos factores, entre ellos el costo de los equipos y reactivos, el costo de contratar analistas y la cantidad de muestras que se pueden procesar por hora. En general, los métodos que dependen de instrumentos cuestan más por muestra que otros métodos.
Haciendo la elección final
Desafortunadamente, los criterios de diseño discutidos en esta sección no son mutuamente independientes [Valcárcel, M.; Ríos, A. Anal. Chem. 1993, 65, 781A—787A]. Trabajar con muestras más pequeñas o mejorar la selectividad a menudo viene a expensas de la precisión. Minimizar costos y tiempo de análisis puede disminuir la precisión. Seleccionar un método requiere equilibrar cuidadosamente los diversos criterios de diseño. Por lo general, el criterio de diseño más importante es la precisión, y el mejor método es el que da el resultado más preciso. Cuando la necesidad de un resultado es urgente, como suele ser el caso en los laboratorios clínicos, el tiempo de análisis puede convertirse en el factor crítico.
En algunos casos son las propiedades de la muestra las que determinan el mejor método. Una muestra con una matriz compleja, por ejemplo, puede requerir un método con excelente selectividad para evitar interferencias. Las muestras en las que el analito está presente a una concentración traza o ultratraza generalmente requieren un método de concentración. Si la cantidad de muestra es limitada, entonces el método no debe requerir una gran cantidad de muestra.