3.1: Amplificadores Operacionales

Un amplificador operacional (o amplificador operacional, para abreviar) es un circuito eléctrico que tiene una variedad de usos, algunos de los cuales consideramos en esta sección: cómo amplificar y medir la señal de un transductor (detector), y cómo realizar operaciones matemáticas sobre señales. En esta sección proporcionaremos una visión básica de los amplificadores operativos sin preocuparnos por los detalles internos específicos de su circuito eléctrico.

Nota

Un excelente recurso para esta sección y otras secciones de este capítulo es Principios de Instrumentación Electrónica de A. James Diefenderfer y publicado por W. B. Saunders Company, 1972.

Representación simbólica de un amplificador operacional

La figura\(\PageIndex{1}\) proporciona una representación simbólica de un amplificador operacional. La forma triangular grande es el amplificador operacional, que es un circuito extenso cuyo diseño exacto no nos interesa; así, la forma simple. El amplificador operacional tiene dos entradas de voltaje que se identifican como\(v_{-}\) y como\(v_{+}\) y etiquetadas como\(-\) y\(+\) en el amplificador operacional. La diferencia entre\(v_{-}\) y\(v_{+}\) se define como\(v_{s}\). El amplificador operacional también tiene una salida de voltaje único que se identifica como\(v_{out}\). Todos los voltajes se miden con relación a un circuito común de 0 V, representado por el pequeño triángulo en la parte inferior de la figura, que proporciona una referencia compartida; se entiende que el circuito común está presente incluso cuando no se muestra. No se incluyen en esta cifra las conexiones a una fuente de alimentación, que son necesarias para su funcionamiento.

Figura\(\PageIndex{1}\). Representación de un amplificador operacional. Consulte el texto para más detalles.

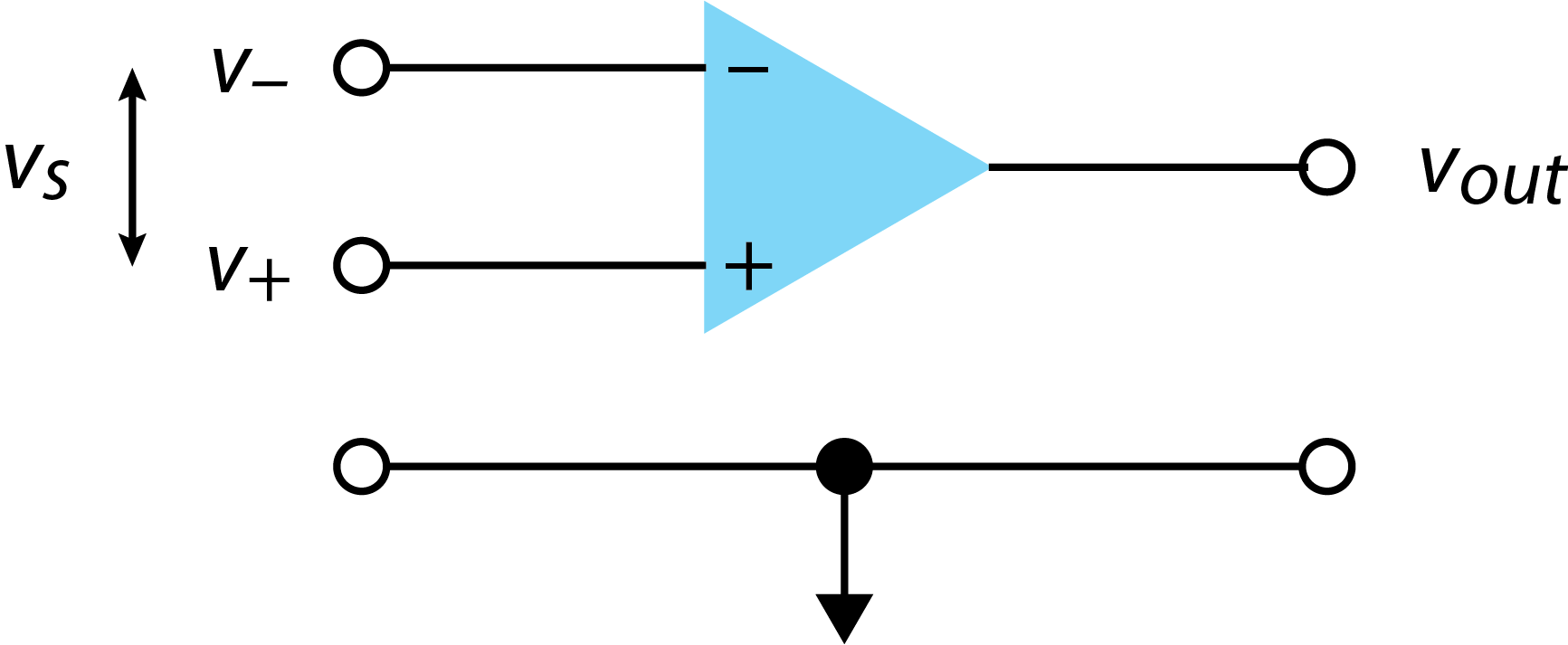
Entradas inversoras y no inversoras

El signo menos y el signo más que aparecen como etiquetas en el amplificador operacional en la Figura\(\PageIndex{1}\) no significan que una entrada tenga un valor positivo y que la otra entrada tenga un valor negativo. En cambio, se invierte una entrada al cable con un signo negativo: si\(v_{-}\) es un voltaje de CC negativo, entonces el voltaje de salida,\(v_{out}\), es un voltaje de CC positivo, y si\(v_{-}\) es un voltaje de CC positivo, entonces el voltaje de salida,\(v_{out}\), es un voltaje de CC negativo. Para una entrada de CA a\(v_{-}\), la salida está desfasada 180°, lo que implica una inversión en el signo. La otra entrada al amplificador operacional es no inversora, lo que significa que aplicar un voltaje positivo a\(v_{+}\) los resultados en una señal positiva en\(v_{out}\).

Propiedades Clave de Amplificadores Operacionales

El amplificador operacional ideal tiene varias propiedades importantes que derivan de su circuitería interna. La primera de estas propiedades es que la ganancia del amplificador operacional\(A\), que se define como la relación entre el voltaje de salida y el voltaje de entrada

\[A_{op} = - \frac{v_{out}}{v_{s}} = - \frac{v_{out}}{v_{-} - v_{+}} \label{prop1} \]

es muy grande, típicamente del orden de 10 ⁴ — 10 ⁶. Debemos tener cuidado cuando usamos el término ganancia ya que puede haber una diferencia significativa entre la ganancia del amplificador operacional y la ganancia del circuito que contiene el amplificador operacional. La ganancia del amplificador operacional, que es lo que queremos decir con Ecuación\ ref {prop1}, se llama ganancia de bucle abierto. La ganancia de un circuito que contiene un amplificador operacional se denomina ganancia de bucle cerrado. Donde haya ambigüedad, tendremos cuidado de referirnos a la ganancia del amplificador operacional\(A_{op}\), o a la ganancia del circuito\(A_c\), ya que estos son más descriptivos.

Una segunda propiedad de un amplificador operacional es que independientemente de los valores específicos de\(v_{-}\) y\(v_{+}\), el circuito interno del amplificador operacional está diseñado de tal manera que la corriente entre las dos entradas es efectivamente cero; en esencia, la impedancia,\(Z\), entre las dos entradas es tan grande que desde Ley de Ohm\(V = I \times Z\),, la corriente entre estas dos entradas es\(I \approx 0\). Una gran impedancia de entrada significa que podemos conectar nuestro amplificador operacional a una fuente de alto voltaje y saber que extraerá una pequeña corriente en lugar de sobrecargar el circuito que incluye el amplificador operacional.

Una tercera propiedad de un amplificador operacional es que su impedancia de salida es muy pequeña, lo que significa que podemos extraer una corriente del circuito que satisfaga nuestras necesidades, esta corriente se extrae de la fuente de alimentación del amplificador operacional, incluso si la corriente en el amplificador operacional es cero. Por ejemplo, si la ganancia del circuito es pequeña, podemos usar el amplificador operacional para proporcionar una gran ganancia de corriente.