23.5: Instrumentos para medir potenciales celulares
- Page ID
- 78983
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Para medir el potencial de una celda electroquímica de una manera que esencialmente no consume corriente, utilizamos un potenciómetro. Para ayudarnos a entender cómo un potenciómetro logra esto, describiremos el instrumento como si el analista lo estuviera operando manualmente. Para ello, el analista observa un cambio en la corriente o el potencial y ajusta manualmente los ajustes del instrumento para mantener las condiciones experimentales deseadas. Es importante entender que los instrumentos electroquímicos modernos proporcionan un medio electrónico automatizado para controlar y medir la corriente y el potencial, y que lo hacen mediante el uso de circuitos electrónicos muy diferentes a los descritos aquí.
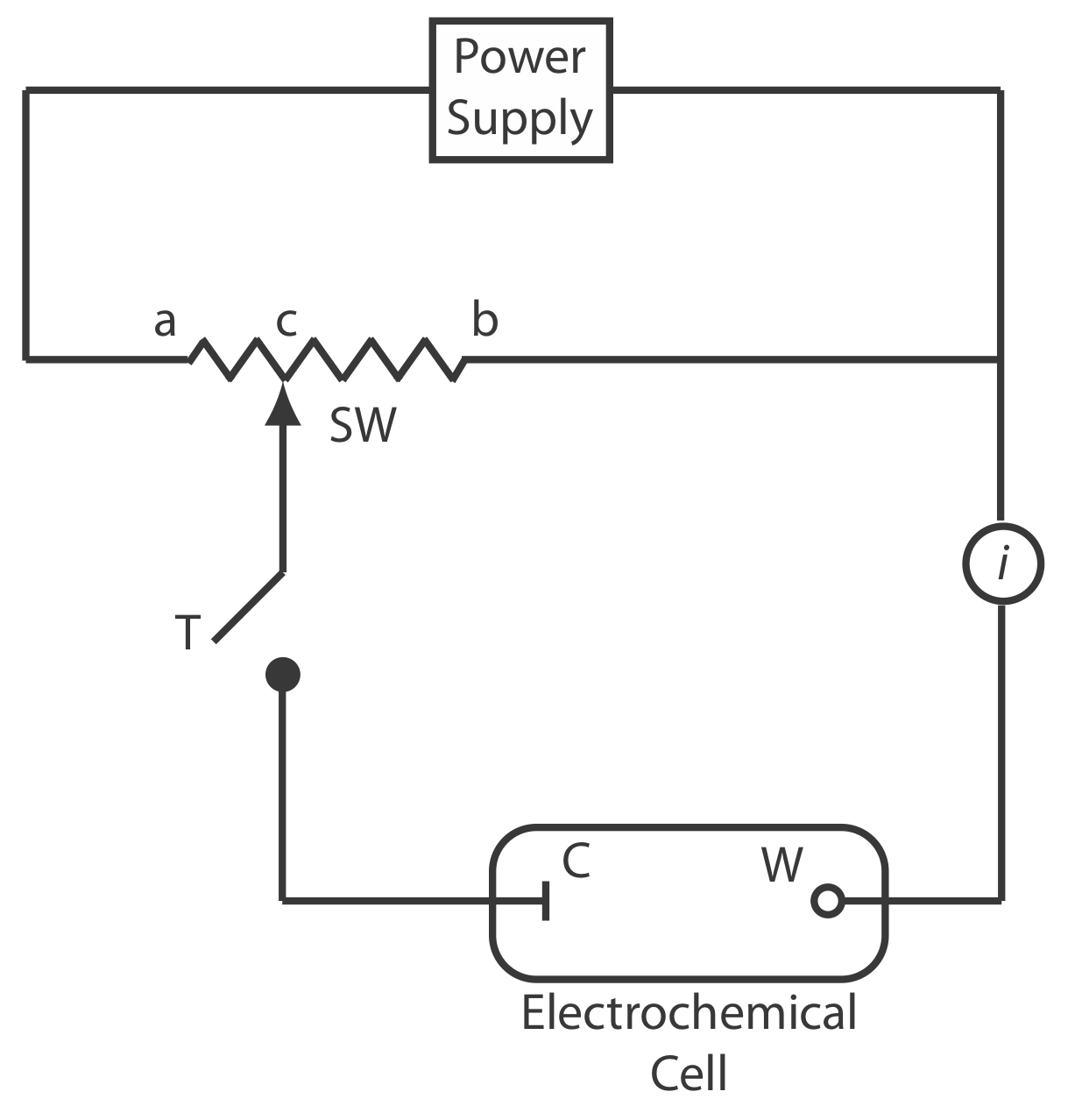
La figura\(\PageIndex{1}\) muestra un diagrama esquemático de un potenciómetro manual que consiste en una fuente de alimentación, una celda electroquímica con un electrodo de trabajo y un contraelectrodo, un amperímetro para medir la corriente que pasa a través de la celda electroquímica, una resistencia ajustable de cable deslizante y una tecla de toma para cerrar el circuito a través de la celda electroquímica. Usando la ley de Ohm, la corriente en la mitad superior del circuito es
\[i_{\text {upper}}=\frac{E_{\mathrm{PS}}}{R_{a b}} \label{pot1} \]
donde E PS es el potencial de la fuente de alimentación y R ab es la resistencia entre los puntos a y b de la resistencia de cable deslizante. De manera similar, la corriente en la mitad inferior del circuito es
\[i_{\text {lower}}=\frac{E_{\text {cell}}}{R_{c b}} \label{pot2} \]
donde la celda E es la diferencia de potencial entre el electrodo de trabajo y el contraelectrodo, y R cb es la resistencia entre los puntos c y b de la resistencia de cable deslizante. Cuando i superior = i inferior = 0, no fluye corriente a través del amperímetro y el potencial de la celda electroquímica es
\[E_{\mathrm{coll}}=\frac{R_{c b}}{R_{a b}} \times E_{\mathrm{PS}} \label{pot3} \]
Para determinar la celda E presionamos brevemente la tecla tap y observamos la corriente en el amperímetro. Si la corriente no es cero, entonces ajustamos la resistencia del cable deslizante y volvemos a medir la corriente, continuando con este proceso hasta que la corriente sea cero. Cuando la corriente es cero, usamos la Ecuación\ ref {pot3} para calcular la celda E.
El uso de la tecla tap para cerrar brevemente el circuito a través de la celda electroquímica minimiza la corriente que pasa a través de la celda y limita el cambio en la composición de la celda electroquímica. Por ejemplo, pasar una corriente de 10 —9 A a través de la celda electroquímica durante 1 s cambia las concentraciones de especies en la celda en aproximadamente 10 —14 moles.
\[10^{-9} \text{ A} = 10^{-9} \text{ C/s} \label{pot4} \]
\[10^{-9} \text{ C/s} \times 1 \text{ s} \times \frac {1 \text{ mol}} {96485 \text{C}} = 1.0 \times 10^{-14} \text{ mol} \label{pot5} \]
Por supuesto, tratar de medir un potencial de esta manera es tedioso. Los potenciómetros modernos utilizan amplificadores operacionales para crear un voltímetro de alta impedancia que mide el potencial mientras extrae una corriente de menos de\(10^{–9}\) A. El error relativo,\(E_r\), en el potencial medido
\[E_r = \frac {R_\text{cell}} {R_\text{meter} + R_\text{cell}} \label{pot6} \]
donde\(R_\text{cell}\) está la resistencia de la solución en la celda electroquímica y\(R_\text{meter}\) es la resistencia del medidor. Para una solución con una resistencia de\(10 \text{M}\Omega\) para lograr un error relativo de\(-0.1\%)\) o\(-0.001\) requiere una\(R_\text{meter}\) de
\[-0.001 = \frac {-10 \text{ M}\Omega} {R_\text{meter} + 10 \text{ M}\Omega} \nonumber \]
\[-0.001 \times R_\text{meter} - 0.01 = -10 \text{ M}\Omega \nonumber \]
\[-0.001 \times R_\text{meter} = -9.990 \text{ M}\Omega \nonumber \]
\[R_\text{meter} = 9990 \text{ M}\Omega \nonumber \]