23.6: Potenciometría Cuantitativa
- Page ID
- 78976
La aplicación más importante de la potenciometría es determinar la concentración de un analito en solución. La mayoría de los electrodos potenciométricos son selectivos hacia la forma libre y no complejada del analito, y no responden a ninguna de las formas complejadas del analito. Esta selectividad proporciona a los electrodos potenciométricos una ventaja significativa sobre otros métodos cuantitativos de análisis si es necesario determinar la concentración de iones libres. Por ejemplo, el calcio está presente en la orina tanto como iones Ca 2 + libres como iones Ca 2 + unidos a proteínas. Si analizamos una muestra de orina mediante espectroscopia de absorción atómica, la señal es proporcional a la concentración total de Ca 2 + porque tanto el calcio libre como el unido están atomizados. El análisis de orina con un ISE Ca 2 +, sin embargo, da una señal que es función solo de iones Ca 2 + libres porque el Ca 2 + unido a proteína no puede interactuar con la membrana del electrodo. En esta sección, consideramos varios aspectos importantes de la potenciometría cuantiativa.
La relación entre concentración y potencial
En el Capítulo 23.3, mostramos que el potencial de un electrodo selectivo de iones para un ion con una carga de z es
\[E_{\mathrm{cell}}=K+\frac{0.05916}{z} \log \left(a_{A}\right)_{\mathrm{samp}} \label{quant1} \]
donde K es una constante que incluye los potenciales de los electrodos de referencia internos y externos del electrodo selectivo de iones, cualquier potencial de asimetría asociado con la membrana del electrodo selectivo de iones y la actividad del analito en la solución interna del electrodo selectivo de iones. La ecuación\ ref {quant1} es una ecuación general y se aplica a todos los tipos de electrodos selectivos de iones. Tenga en cuenta que cuando el analito es un catión, un aumento en la actividad del analito da como resultado un aumento en el potencial; cuando el analito es un anión, lo que hace que z sea un número negativo, un aumento en la actividad del analito da como resultado una disminución en el potencial.
Como las concentraciones de iones en solución a menudo se reportan como valores de pX, donde
\[\text{pX} = - \log a_\text{X} \label{quant2} \]
es conveniente sustituir la ecuación\ ref {quant2} por la ecuación\ ref {quant1}
\[E_{\mathrm{cell}}=K - \frac{0.05916}{z} \text{ pA} \label{quant3} \]
Tenga en cuenta que para un catión, un aumento en pA resulta en una disminución en el potencial; cuando el analito es un anión, un aumento en pA da como resultado un aumento en el potencial.
Calibración de electrodos potenciométricos
Para usar la Ecuación\ ref {quant3} necesitamos determinar el valor de K, lo cual podemos hacer usando uno o más estándares externos o por el método de adición estándar, ambos de los cuales fueron cubiertos en el Capítulo 1.5. Una complicación, por supuesto, es que el potencial es una función de la actividad del analito en lugar de su concentración.
Actividad y Concentración
La ecuación\ ref {quant1} se escribe en términos de la actividad del analito. Sin embargo, cuando usamos un electrodo potenciométrico, nuestro objetivo es determinar la concentración del analito. Como aprendimos en el Capítulo 22, la actividad de un ión es producto de su concentración, [M n +], y un coeficiente de actividad dependiente de la matriz,\(\gamma_{Mn^{n+}}\).
\[a_{M^{n+}}=\left[M^{n+}\right] \gamma_{M^{n+}} \label{quant4} \]
Sustituyendo la ecuación\ ref {quant4} en Ecuación\ ref {quant1} y reordenando, da
\[E_{\mathrm{cell}}=K+\frac{0.05916}{n} \log \gamma_{M^{n+}}+\frac{0.05916}{n} \log \left[M^{n+}\right] \label{quant5} \]
Podemos resolver la Ecuación\ ref {quant5} para la concentración del ión metálico si conocemos el valor de su coeficiente de actividad. Desafortunadamente, si no conocemos la composición iónica exacta de la matriz de la muestra, que es la situación habitual, entonces no podemos calcular el valor de\(\gamma_{Mn^{n+}}\). Hay una solución a este dilema. Si diseñamos nuestro sistema para que los estándares y las muestras tengan una matriz idéntica, entonces el valor de\(\gamma_{Mn^{n+}}\) permanece constante y Ecuación\ ref {quant5} simplifica a
\[E_{\mathrm{cell}}=K^{\prime}+\frac{0.05916}{n} \log \left[M^{n+}\right] \label{quanat6} \]
donde\(K^{\prime}\) incluye el coeficiente de actividad.
Calibración mediante estándares externos
En ausencia de interferentes, una curva de calibración de célula E versus log a A, donde A es el analito, es una línea recta. Una gráfica de célula E versus log [A], sin embargo, puede mostrar curvatura a concentraciones más altas de analito como resultado de un cambio dependiente de la matriz en el coeficiente de actividad del analito. Para mantener una matriz consistente agregamos una alta concentración de un electrolito inerte a todas las muestras y estándares. Si la concentración de electrolito agregado es suficiente, entonces la diferencia entre la matriz de la muestra y la matriz de los estándares no afectará la fuerza iónica y el coeficiente de actividad esencialmente permanece constante. El electrolito inerte agregado a la muestra y los estándares se denomina tampón de ajuste de fuerza iónica total (TISAB).
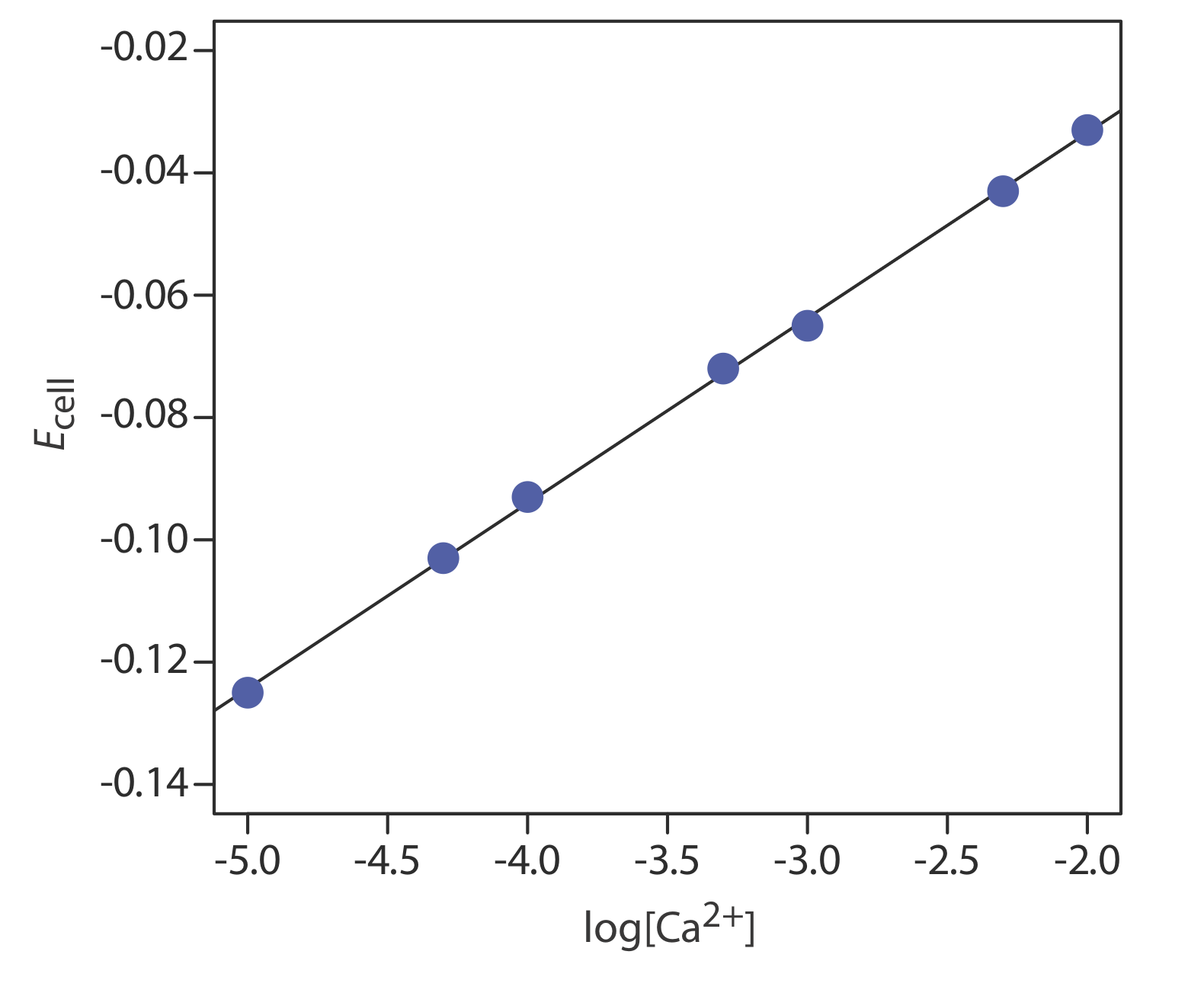
La concentración de Ca 2 + en una muestra de agua se determina mediante el método de estándares externos. La fuerza iónica de las muestras y los estándares se mantiene a un nivel casi constante haciendo que cada solución sea 0.5 M en KNO 3. Los potenciales celulares medidos para los estándares externos se muestran en la siguiente tabla.
| [Ca 2 +] (M) | Celda E (V) |
|---|---|
| \(1.00 \times 10^{-5}\) | —0.125 |
| \(5.00 \times 10^{-5}\) | —0.103 |
| \(1.00 \times 10^{-4}\) | —0.093 |
| \(5.00 \times 10^{-4}\) | —0.072 |
| \(1.00 \times 10^{-3}\) | —0.063 |
| \(5.00 \times 10^{-3}\) | —0.043 |
| \(1.00 \times 10^{-2}\) | —0.033 |
¿Cuál es la concentración de Ca 2 + en una muestra de agua si se encuentra que su potencial celular es —0.084 V?
Solución
La regresión lineal da la curva de calibración en la Figura\(\PageIndex{1}\), con una ecuación de
\[E_{\mathrm{cell}}=0.027+0.0303 \log \left[\mathrm{Ca}^{2+}\right] \nonumber \]
Sustituir el potencial celular de la muestra da la concentración de Ca 2 + como\(2.17 \times 10^{-4}\) M. Obsérvese que la pendiente de la curva de calibración, que es 0.0303, es ligeramente mayor que su valor ideal de 0.05916/2 = 0.02958; esto no es inusual y es una razón para usar múltiples estándares. Una razón por la que no es inusual encontrar que la pendiente experimental se desvía de su valor ideal de 0.05916/ n es que este valor ideal supone que la temperatura es de 25°C.
Calibración mediante adiciones estándar
Otro enfoque para calibrar un electrodo potenciométrico es el método de adiciones estándar, el cual se introdujo en el Capítulo 1.5. Primero, transferimos una muestra con un volumen de V samp y una concentración de analito de C samp a un vaso de precipitados y medimos el potencial, (célula E) samp. A continuación, hacemos una adición estándar agregando a la muestra un pequeño volumen, V std, de un estándar que contiene una concentración conocida de analito, C std, y medimos el potencial, (celda E) std. Si V std es significativamente menor que V samp, entonces podemos ignorar con seguridad el cambio en la matriz de la muestra y asumir que el coeficiente de actividad del analito es constante. Ejemplo\(\PageIndex{9}\) demuestra cómo podemos usar una adición estándar de un punto para determinar la concentración de analito en una muestra.
La concentración de Ca 2 + en una muestra de agua de mar se determina usando un electrodo selectivo de iones Ca y una adición estándar de un punto. Una muestra de 10.00 ml se transfiere a un matraz aforado de 100 ml y se diluye a volumen. Se coloca una alícuota de 50.00-mL de la muestra en un vaso de precipitados con el ISE de Ca y un electrodo de referencia, y el potencial se mide como —0.05290 V. Después de agregar una alícuota de 1.00-mL de una solución estándar\(5.00 \times 10^{-2}\) M de Ca 2 + el potencial es —0.04417 V. Cuál es la concentración de Ca 2 + en la muestra de agua de mar?
Solución
Para comenzar, escribimos la ecuación de Nernst antes y después de agregar la suma estándar. El potencial celular para la muestra es
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{samp}}=K+\frac{0.05916}{2} \log C_{\mathrm{samp}} \nonumber \]
y que siguiendo la adición estándar es
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{std}}=K+\frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} \nonumber \]
donde V tot es el volumen total (V samp + V std) después de la adición estándar. Restar la primera ecuación de la segunda ecuación da
\[\Delta E = \left(E_{\mathrm{cell}}\right)_{\mathrm{std}} - \left(E_{\mathrm{cell}}\right)_{\mathrm{samp}} = \frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} - \frac{0.05916}{2}\log C_\text{samp} \nonumber \]
Reorganizar esta ecuación nos deja con
\[\frac{2 \Delta E_{cell}}{0.05916} = \log \left\{ \frac {V_\text{samp}} {V_\text{tot}} + \frac {V_\text{std}C_\text{std}} {V_\text{tot}C_\text{samp}} \right\} \nonumber \]
Sustituyendo valores conocidos por\(\Delta E\), V samp, V std, V tot y C std,
\[\begin{array}{l}{\frac{2 \times\{-0.04417-(-0.05290)\}}{0.05916}=} \\ {\log \left\{\frac{50.00 \text{ mL}}{51.00 \text{ mL}}+\frac{(1.00 \text{ mL})\left(5.00 \times 10^{-2} \mathrm{M}\right)}{(51.00 \text{ mL}) C_{\mathrm{samp}}}\right\}} \\ {0.2951=\log \left\{0.9804+\frac{9.804 \times 10^{-4}}{C_{\mathrm{samp}}}\right\}}\end{array} \nonumber \]
y tomando el log inverso de ambos lados da
\[1.973=0.9804+\frac{9.804 \times 10^{-4}}{C_{\text {samp }}} \nonumber \]
Finalmente, resolviendo para C samp da la concentración de Ca 2 + como\(9.88 \times 10^{-4}\) M. Debido a que diluimos la muestra original de agua de mar por un factor de 10, la concentración de Ca 2 + en la muestra de agua de mar es\(9.88 \times 10^{-3}\) M.
La definición operativa de pH
Con la disponibilidad de electrodos de pH de vidrio de bajo costo y medidores de pH, la determinación del pH es una de las mediciones analíticas cuantitativas más comunes. La determinación potenciométrica del pH, sin embargo, no está exenta de complicaciones, varias de las cuales discutimos en esta sección.
Una complicación es la confusión sobre el significado del pH [Kristensen, H. B.; Saloman, A.; Kokholm, G. Anal. Chem. 1991, 63, 885A—891A]. La definición convencional de pH en la mayoría de los libros de texto de química general se da en términos de la concentración de H +
\[\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right] \label{quant7} \]
Como ahora sabemos, cuando medimos el pH en realidad es una medida de la actividad de H +.
\[\mathrm{pH}=-\log a_{\mathrm{H}^{+}} \label{quant8} \]
Pruebe este experimento: encuentre varios libros de texto de química general y busque el pH en el índice de cada libro de texto. Diríjase a las páginas correspondientes y vea cómo se define. A continuación, busque actividad o coeficiente de actividad en el índice de cada libro de texto y vea si estos términos están indexados.
La ecuación\ ref {quant7} solo se aproxima al pH verdadero. Si calculamos el pH de HCl 0.1 M usando la Ecuación\ ref {quant7}, obtenemos un valor de 1.00; el pH real de la solución, definido por la Ecuación\ ref {quant8}, es 1.1 [Hawkes, S. J. J. Chem. Educ. 1994, 71, 747—749]. La actividad y la concentración de H + no son las mismas en HCl 0.1 M porque el coeficiente de actividad para H + no es 1.00 en esta matriz. La figura\(\PageIndex{2}\) muestra una demostración más colorida de la diferencia entre actividad y concentración.
Una segunda complicación en la medición del pH es la incertidumbre en la relación entre potencial y actividad. Para un electrodo de membrana de vidrio, el potencial celular, (celda E) samp, para una muestra de pH desconocido es
\[(E_{\text{cell}})_\text {samp} = K-\frac{R T}{F} \ln \frac{1}{a_{\mathrm{H}^{+}}}=K-\frac{2.303 R T}{F} \mathrm{pH}_{\mathrm{samp}} \label{quant9} \]
donde K incluye el potencial del electrodo de referencia, el potencial de asimetría de la membrana de vidrio y cualquier potencial de unión en la celda electroquímica. Todas las contribuciones a K están sujetas a incertidumbre, y pueden cambiar del día a día, así como de electrodo a electrodo. Por esta razón, antes de usar un electrodo de pH lo calibramos usando un tampón estándar de pH conocido. El potencial celular para el estándar, (celda E) std, es
\[\left(E_{\text {ccll}}\right)_{\text {std}}=K-\frac{2.303 R T}{F} \mathrm{p} \mathrm{H}_{\mathrm{std}} \label{quant10} \]
donde pH std es el pH del estándar. Restar la ecuación\ ref {quan10} de la ecuación\ ref {quant9} y resolviendo para pH samp da
\[\text{pH}_\text{samp} = \text{pH}_\text{std} - \frac{\left\{\left(E_{\text {cell}}\right)_{\text {samp}}-\left(E_{\text {cell}}\right)_{\text {std}}\right\} F}{2.303 R T} \label{quant11} \]
que es la definición operativa de pH adoptada por la Unión Internacional de Química Pura y Aplicada [Covington, A. K.; Bates, R. B.; Durst, R. A. Pure & Appl. Chem. 1985, 57, 531—542].
Calibrar un electrodo de pH presenta una tercera complicación porque necesitamos un estándar con una actividad conocida con precisión para H +. \(\PageIndex{1}\)La tabla proporciona valores de pH para varias soluciones tampón estándar primarias aceptadas por el Instituto Nacional de Estándares y Tecnología.
Para estandarizar un electrodo de pH usando dos tampones, elija uno cercano a un pH de 7 y otro que sea más ácido o básico dependiendo del pH esperado de su muestra. Enjuague su electrodo de pH en agua desionizada, séquelo con una toallita de laboratorio y colóquelo en el tampón con el pH más cercano a 7. Gira el electrodo de pH y deja que se equilibre hasta obtener una lectura estable. Ajuste la perilla “Estandarizar” o “Calibrar” hasta que el medidor muestre el pH correcto. Enjuague y seque el electrodo, y colóquelo en el segundo tampón. Después de que el electrodo se equilibre, ajuste la perilla “Pendiente” o “Temperatura” hasta que el medidor muestre el pH correcto.
Algunos medidores de pH pueden compensar un cambio de temperatura. Para utilizar esta característica, coloque una sonda de temperatura en la muestra y conéctelo al medidor de pH. Ajuste el botón “Temperatura” a la temperatura de la solución y calibra el medidor de pH usando los controles “Calibrar” y “Pendiente”. Al usar el electrodo de pH, el medidor de pH compensa cualquier cambio en la temperatura de la muestra ajustando la pendiente de la curva de calibración usando una respuesta nernstiana de 2.303 RT/F.